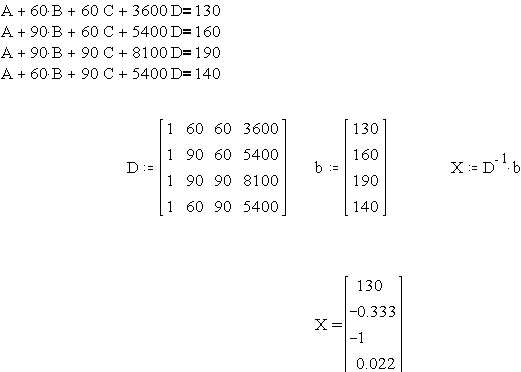GIS műveletek IV

Ebben a részben néhány olyan GIS funkciót tárgyalunk, melyek eredetileg nem tartoztak a kvázi szabványos GIS függvénykészlethez, de napjainkban már a GIS leghatékonyabb tervezési eszközeit képviselik.

Megismerkedünk néhány elemi modellezési feladattal, ezeken belül

a domborzat modellezés néhány kérdésével,
a hálózati modellezés fogalmával és a
folyosó tervezéssel.

Modellezés (domborzat, hálózatok, folyosók)

A földrajzi modellezés nem más mint a különböző térbeli jelenségek egymásra hatásának vizsgálata, s ezek eredményeinek meghatározása alapján jelenségek, tulajdonságok vagy folyamatok várható értékeinek prognosztizálása.
Az előre jelzett értékek közvetlen mérése általában problémás vagy lehetetlen. Ez utóbbi érvényes abban az esetben is, ha a vizsgálatot részben vagy egészben szimulált adatokkal végzik. A modellezés során a térinformatikai rendszer szolgáltatja a valódi és szimulált adatokat de tartalmaznia kell a kölcsönhatást leíró algoritmusokat is. Mivel végtelen sok szempontból vizsgálhatjuk a térbeli adatok egymásra hatását nincs arra lehetőség, hogy minden modellező algoritmust beépítsenek a GIS függvénytárába.
Ideális esetben a GIS nyílt rendszer és felhasználónak lehetősége van, hogy saját algoritmusával fejlessze a függvénykészletet. A korszerű kereskedelmi GIS rendszerek rendszerint csak a domborzat modellezés, hálózatelemzés és folyosótervezés eszköztárával rendelkeznek beépített formában.

Domborzatmodellezés

A domborzatmodellezésre nem teljesen érvényesek az előző pont meghatározásában mondottak. Maga a domborzatmodellezés tulajdonképpen nem más, mint a terep ismert magasságainak felhasználásával olyan levezetetett termékek létrehozása, melyek bemenő adatként szerepelnek a domborzat hatásaira érzékeny valódi modellező eljárásokban.

Egy rövid példával próbáljuk világosabbá tenni az elmondottakat. A digitális magasságmodellben szabályos vagy szabálytalan rendszerben elhelyezkedő pontok magasságait tárolják. Ahhoz, hogy megvizsgáljuk egy adott terület várható eróziós pusztulását a csapadék viszonyok, talajtípusok ismerete mellett a terep lejtésére van szükségünk. Az erózió modellezés tehát nem közvetlenül a magasságokat igényli, hanem a belőlük levezethető lejtésviszonyokat ábrázoló fedvényt.
A magasságmodellezés két fő részből áll: a terepi magasságok felhasználásával szabályos vagy szabálytalan magasságmodell létrehozásából, és a modellből levezethető termékek előállításából. Mivel a hivatkozott pontban valamint a szabálytalan esetet tárgyaló részben, ezenkívül az adatnyerés oldaláról is már részletesen foglalkoztunk az első feladattal sőt a magasság interpolálással is, mely tulajdonképpen már a második feladat részét képezi, jelen pontban csak az eddig nem tárgyalt legfontosabb levezetett termékekkel fogunk foglalkozni.

A domborzatot leíró magasságokból levezethető legfontosabb jellemző a lejtés. Szórt pontok esetén a Delaunay háromszögelés segítségével a terepet síkok mozaikjára bontjuk (angol rövidítéssel TIN modellt hozunk létre). A háromszögek lejtési viszonyait viszonylag egyszerű kiszámolni. Írjuk fel a három csúcspontjával adott sík egyenletét:

^(1).

Mivel a lejtés nem más mint a függvény változását jellemző iránytangens szöge, meghatározásához felhasználjuk a függvény növekedését jellemző nabla operátort. Ha a függvényt megszorozzuk a nabla operátorral úgy megkapjuk a függvény növekedését jellemző gradiens vektor koordináta tengelyekre vett vetületeit:

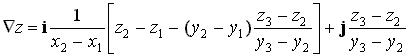^(2).

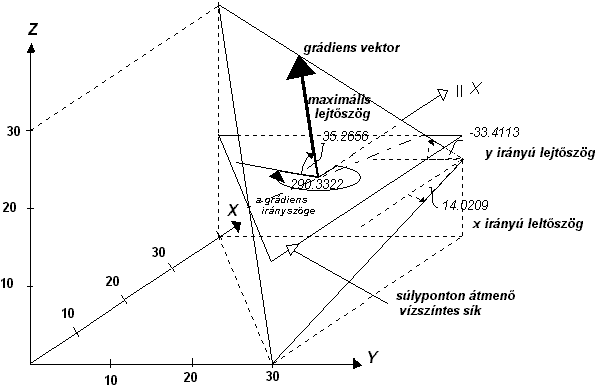
A vetületek felhasználásával Pithagorász tételéből kiszámíthatjuk a gradiens értékét (a maximális lejtéshez tartozó tangens értéket), valamint a vektor szögét valamelyik koordináta tengellyel. A gradiens vektort tekintettel arra, hogy a vizsgált felület sík, bárhol elhelyezhetjük a háromszögben, reprezentatív okok azonban indokolják, hogy a vektort a súlypontba helyezzük. A 4.29 ábrán megpróbáljuk szemléltetni az elmondottakat.

4.29 ábra - lejtési viszonyok a TIN modellben

A maximális lejtés iránya az esésvonal mindig merőleges a lejtő és a vízszintes sík metszésvonalára a szintvonalra. Példánk esetében a maximális lejtő irányának értelme (a vektor nyila) a gradiens értelmezéséből kiindulva a magasságok növekedése irányába mutat. Gyakran a nyilat a csökkenő magasságok felé irányítják.

A domborzatábrázolás gyakran azzal a jelenséggel próbálja szemléltetni a terep térbeli megjelenését, hogy a felületelemek fényvisszaverő képessége, egyéb paraméterek mellett, függ normálisuknak a beeső fénysugarakkal alkotott szögétől. A visszaverődés ebből a szempontból vizsgálva akkor maximális, ha a beeső fénysugár iránya megegyezik a felületelem normálisával. Ábrázolási célból tehát a rendszerek gyakran számítják a felületelem normálisát is, mely értelemszerűen merőleges a legnagyobb esés irányára.

A szabályos négyzetrácsra épített modellek esetén (angol rövidítésük DEM) a lejtés meghatározása már nem ennyire egyszerű. A négy adott magasság segítségével a rácson belüli, nem tárolt pontok magasságait bilineáris interpolációval számolhatjuk. A rácson belüli felületet ebben az esetben a

z=A+Bx+Cy+Dxy

(3)

kifejezésből számolhatjuk. Ha például a 4.30 ábrán látható rácsszemet kívánjuk modellezni, úgy az ábrán szereplő koordináták és magasságok (60,60,130; 90,60,160; 90,90,190; 60,90,140) segítségével a (3)-ban szereplő együtthatók az alábbiak lesznek (az együtthatókat az X vektorban foglaltuk össze):

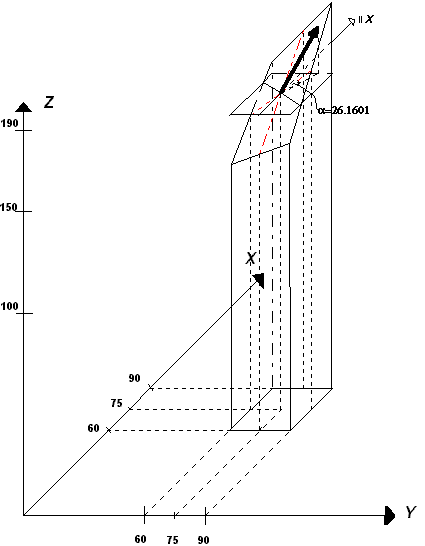
Számunkra a lejtőviszonyok szempontjából azonban a gradiens vektor az érdekes, mely a példa esetén a következő kifejezésekből számolható:

(4).

4.30 ábra - lejtési viszonyok a DEM modellben

A (4) kifejezésből látható, hogy a maximális lejtés a cellán belül is pontról pontra változik. A cellára jellemző maximális lejtést és lejtőirányt többféle meggondolás alapján is számíthatnánk, talán a legmeggyőzőbb ebben az esetben is, ha a cella súlypontjában számított gradiens értéket vonatkoztatjuk az egész cellára.
Példánkban mivel mind a két súlyponti koordináta x_s=y_s=75, a gradiens x irányú komponense 1,317, ami 52.4726 lejtésnek felel meg fok.percmásodperc egységben kifejezve, y irányú komponense pedig 0.65 illetve az y irányú lejtőszög 33.0126. A gradiens vektor abszolút értéke 1.469, a súlyponti maximális lejtés 55.4458, a lejtés irányszöge pedig 26.1606.

A lejtő nagyságok és irányok kiszámítása alapján a különböző GIS szoftverek különböző levezetett műveletek végrehajtására is alkalmasak.
A legegyszerűbb művelet kis nyilak segítségével szemlélteti minden háromszög vagy raszter cella súlypontjában a lejtést: a nyilak hossza arányos a lejtés nagyságával, iránya pedig a maximális lejtés irányába mutat.

Bonyolultabb feladat, bár sok rendszer képes rá, a 4.21 ábrán már bemutatott és felhasznált lejtőkategória térkép létrehozása.
A felhasználó megadja, hogy milyen határok között kíván egy-egy lejtőkategória osztályt létrehozni. A program kiválasztja az egy-egy osztályba tartozó háromszögeket vagy cellákat, az egy osztályon belüli szomszédos elemeket egy objektumba olvasztja és közös határát megszünteti és az egy új osztályhoz tartozó objektumokat azonos a felhasználó által definiált színnel tölti ki. Természetesen az új objektumok attribútum táblája is megváltozik, s abban csak az új objektumra állandó tulajdonságok jelennek meg.

Egyes rendszerek beépített függvény formájában kezelnek a lejtésviszonyoktól is függő környezeti vizsgálatokat is. E rendszerekben megvizsgálhatjuk, hogy egy bizonyos terepponttól távolodva különböző irányokban azonos idő alatt mennyi utat teszünk meg. Ugyanez a modell különböző járművekre is kidolgozható, ebben az esetben segítségével járhatósági térképeket lehet létrehozni.
Természetesen mind a gyalogos haladási sebesség, mind a különböző járművekkel való járhatóság nem csak a lejtőviszonyoktól, hanem több egyéb körülménytől - például a talajtól, a növényzettől, a vízfelületektől stb. is függ, ezért a megbízhatóbb többváltozós elemzés előtt a kérdéses faktorokat tartalmazó rétegeket fedésbe hozva olyan kompozit réteget kell létrehozni, mely objektumaiban a kérdéses tényezők konstansként szerepelnek. Az összetettebb elemzés rendszerint programfejlesztői munkát is igényel.

A domborzatmodellezés talán legelterjedtebb alkalmazása a vízgyűjtőterületek lefolyási viszonyainak elemzéséhez kapcsolódik. Sok rendszer képes a vízgyűjtőterület automatikus lehatárolására, a vízválasztó vonal meghatározására.

Vegyünk fel a völgyben a folyón egy pontot. Mivel a víz mindig a legmeredekebb lejtő irányába folyik nincs más dolgunk mint a pontból kiinduló esésvonalat elemről elemre követve létrehozni a vízgyűjtőt határoló zárt poligonnak a vízválasztóig tartó részét. A lehatárolást a vízválasztón hasonló elvek alapján folytatja a program azzal a különbséggel, hogy a szomszédos elemek közül nem csak emelkedő de lejtő elemeket is kiválaszthat, ha azok lejtése kisebb a szomszédos két elem lejtésénél. Az elmondottak akkor vezetnek eredményre, ha a keresés a pontból mindkét irányban (mindkét legmeredekebb szomszéd irányában) szimultán kezdődik.

Az elmondottakat közvetlenül a TIN modell esetében alkalmazhatjuk. Raszteres modell esetén az adott magasságokat úgy tekinthetjük, mint egy elemi négyzet középpontját. Hasonlóan a második fejezet 2.27 ábrájához a víz a központi cellába 8 irányból érkezhet: 0=K, 1=ÉK, 2=É, 3=ÉNY, 4=NY, 5=DNY, 6=D, 7=DK. Kisebb felbontású modellekben csak 4 lehetséges folyási irányt alkalmaznak : 0=K, 1=É, 2=NY, 3=D.
Amikor egy pont vízgyűjtő területét kívánják meghatározni megnézik, hogy a 8 vagy 4 szomszédos cella közül melyekből folyik a víz a vizsgált cellába, azaz, hogy mely szomszédos cellák számára a legalacsonyabb szomszéd a vizsgált cella. Az így nyert kiválasztott cellákat egyenként hasonlóképpen megvizsgálják, hogy melyik cellákból folyik beléjük a víz és az eljárást mindaddig folytatják, míg olyan új cellát találnak, melyből a víz valamelyik már kiválasztott cella felé áramlik. Az eredmény egy zárt poligon lesz, melyet a vizsgált pontból kiindulva a kiválasztott szélső cellák összekötésével nyernek.

Bonyolultabb a vízgyűjtő területeken belüli lefolyási viszonyok modellezése. A víz ugyanis kis csapadék mennyiség esetén a felületen folyik, a nagyobb mennyiségek azonban az erózió, defláció által kialakított csatornákon vonulnak le. A szabályos raszter (DEM) felbontása azonban elvileg sem lehet olyan nagy, hogy minden kisebb bevágódást tartalmazzon. A vízgyűjtő hálózat modellezésénél ezért azzal a feltételezéssel élnek, hogy azokban a cellákban alakulnak ki levezető csatornák, ahol a lefolyó víz mennyisége egy küszöbértéket meghalad. Az eljárás során először minden cella egységnyi értékű csapadékot kap. Ezután megnézik, hogy hány cella folyik be egy-egy vizsgált cellába és ha ez az érték meghaladja a határmennyiséget, akkor a kérdéses cella egy csatorna része lesz.
A modellezéssel nyert eredmény a DTM alacsony felbontása következtében csak megközelíti a valóságot, tervezési célokból célszerűbb olyan DTM-et alkalmazni, mely ki van egészítve a terep vízrajzát ábrázoló fedvénnyel.

Hálózatok

A gyakorlati életben nagyon sokszor találkozunk a hálózat fogalmával anélkül, hogy mélyebben elgondolkodnánk a hálózatok mibenlétén. A mai kor embere nehezen képzeli el az életet elektromos áram nélkül, mely a hálózaton keresztül jut el a fogyasztóhoz, ugyanezt mondhatjuk a vezetékes víz-szolgáltatásról, a telefonszolgáltatásról, a gázszolgáltatásról, távhőellátásról, szennyvízelvezetésről stb. Nem képzelhető el a korszerű közlekedés sem út-, illetve vasúthálózat nélkül. Általánosítva tehát megállapíthatjuk, hogy a hálózatoknak olyan összefüggő vezetékrendszert nevezünk, melyek biztosítják a mozgó erőforrások helyváltoztatását.

A hálózatok bizonyos tulajdonságai egyszerűbben modellezhetők, ha a gráfelmélet eszköztárát felhasználva, a hálózat topológiai szerkezetét megőrizve ideiglenesen eltekintünk a rendszer pontos geometriájától, és a csomópontokat összekötő íveket a geometriát is figyelembe vevő levezetett tényezőkkel jellemezzük.

A hálózati műveletek szemléltetésére legjobb eszköznek az úthálózat jellemzői alapján megoldható optimalizálási feladatok tűnnek. E feladatok két alaptípusa

az optimális útvonal keresés illetve
az erőforrás hozzárendelés (allokáció).

4.31 ábra - optimális útvonal keresés

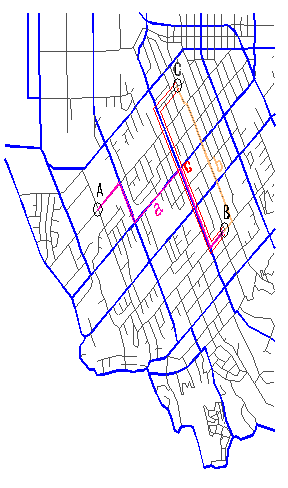
A 4.31-es ábrán egy amerikai város utcahálózatának egy részletét tüntettük fel. Az optimális útvonal keresést az A és B illetve a C és B pontok között végeztük. Míg az első esetben csak egy variánst találtunk az optimális útra, addig a második esetben kettőt. A kapott eredmény azzal magyarázható, hogy az optimális útvonalat több kritérium alapján is kereshetjük. Leggyakrabban a legrövidebb utat keressük, ez az A és B között, a derékszögű amerikai úthálózatnak köszönhetően több egyenlő hosszú variánssal is megoldható, ezek közül egyik az a variáns (a jobb áttekinthetőség érdekében a többi variánst nem tüntettük fel). A C és B pontok között a legrövidebb variáns a c variáns.
Választhatunk azonban más optimalizálási kritériumot is, például kereshetjük a leggyorsabb útvonalat is. Ebben az esetben valószínűsíthető, hogy az az útvonal lesz optimális (b variáns), mely annak ellenére, hogy hosszabb olyan széles főútvonalakon halad, melyeken a haladási sebesség jelentősen meghaladja a mellékutcákon megengedhető értékeket.

Jelen tárgyalásunkban a szemlélet alapján választottuk ki az optimális útvonalakat. Ahhoz, hogy számított adatokból vonjuk le a következtetéseket arra van szükség, hogy a hálózat kapcsolatrendszerét és tulajdonságjellemzőit felhasználó optimalizáló programokat futassunk. Maguk a programok lehetnek a GIS szoftver részei, de lehetnek a felhasználó által fejlesztett GIS-hez csatlakozó programok is. Az alapkövetelmény az a GIS-el szemben, hogy a szükséges adatokat tárolja és hogy ezekhez az adatokhoz a felhasználói programok szabadon hozzáférjenek, másfelől, hogy a kapott eredményeket szemléltesse.

A topológiai adatmodell, mely ívekből és csomópontokból építi fel a hálózatot, az ívek hosszát a töréspontok és csomópontok koordinátáiból kiszámolja és attribútumként tárolja az ívek attribútum táblázatában. Ahhoz azonban, hogy az optimalizálást a legrövidebb időre végezzük szükség van meg egyéb forgalmi jellemzők (sáv szám, burkolat típus, megengedett sebesség, jármű telítettség, stb.) bevitelére az ívek attribútumai közé. Az ívek attribútumait ezen kívül kiegészítik az utca névvel és a címillesztéshez szükséges, mindkét oldali első és utolsó házszámmal.

Az igazi eltérést azonban a tisztán geometriai topológiát kifejező adatmodellhez képest a közlekedési hálózatok csomóponti tulajdonságai jelentik. Míg a geometriai hálózatokban a csomópontba befutó ívek bármelyikéről bármelyik másikra áttérhetünk (a csomópontba befutó ívek kiválasztás szempontjából csak előjelben különbözhetnek) addig a közlekedési hálózatokban a fordulási szabályok, a forgalomirányító lámpák különböző váltás ideje, illetve a nem szabályozott kereszteződések elsőbbségadási és forgalmi viszonyai következtében az ív párokra külön fordulási táblázatok feltöltésére van szükség. Ezekben a táblázatokban minden csomópontra valamennyi lehetséges fordulási irányt fel kell tüntetni és ellátni a jellemző forgalmi időszakokra meghatározott (mért) átlagos fordulási idővel.

A házszámokra az útkeresésben akkor van szükség, ha nem csak csomópontok között kívánunk navigálni. Még nagyobb lehet a címillesztés jelentősége a különböző hozzárendelési feladatokban.

Amint a bevezetőben már szóltunk róla a hozzárendelési feladatok az erőforrások és felhasználóik optimális illesztését célozzák meg. Ezek közé a feladatok közé tartozik például az iskolakörzetek, választási körzetek kijelölése, buszmegállók meghatározása, rendőrjárőr által bejárandó útvonalak meghatározása, bevásárló központok helyének kijelölése, stb.
Minden ilyen jellegű feladatnál két korlátozó tényezőt kell figyelembe venni: a megengedett határértéket és az erőforrás kapacitását. Az iskola körzet kialakításánál például az lehet a határérték, hogy a tanulóknak ne tartson 20 percnél hosszabb ideig az út az iskolába. Kapacitásként, ebben az esetben, az iskola befogadó képességét kell tekinteni.

A térinformatikai rendszer adatbázisa különböző mélységű adatokkal láthatja el a belső vagy külső (a GIS részét képező vagy hozzá fejlesztett) hozzárendelő programokat. A mélység növelésére ebben az esetben is felhasználhatjuk a címillesztést, mivel ennek a segítségével kapcsolhatjuk az utca hálózathoz a népesség nyilvántartási adatbázist. Ha a már hivatkozott iskola körzetesítési feladatra gondolunk, úgy már a határértékekhez is szükség van a címillesztésre, mind az iskola elhelyezése, mind a határértékek házszámmal történő kifejezése szempontjából. Ha ugyanis a címeket nem vonjuk be a határérték vizsgálatba, úgy a körzetek kijelölésénél azzal a közelítéssel kell élnünk, hogy az iskola egy csomópontban van, illetve hogy a körzet határait azok a csomópontok alkotják, melyek elérési ideje nem haladja meg a kitűzött határértéket. A kapacitás vizsgálatához azonban hozzá sem tud fogni a program anélkül, hogy ne álljanak rendelkezésére házszámhoz kapcsoltan az utca lakóinak adatai.

A hálózati feladatok természetesen nem csak az úthálózatra vonatkozhatnak, és nem csak a fentiekben felvázolt két problémára szorítkoznak. Azonban a kereskedelmi szoftverek közül azok, melyek rendelkeznek hálózati modullal kész megoldást rendszerint csak az ismertetett feladatokra nyújtanak. Sokkal jelentősebb azonban e modulok azon képessége, hogy nyitottak új, a felhasználó által fejlesztett programok illesztésére is. Amint már utaltunk rá, ezekben az esetekben a kérdéses GIS fejlesztő környezetében ( a GIS által értelmezett programozási nyelven pld. C⁺⁺, ActiveX, Java) olyan új függvényeket gyártunk, melyek modellezik a kérdéses jelenséget, s ehhez felhasználják a GIS-ben tárolt hálózati fedvényeket s a hozzájuk kapcsolt táblázatokat.

A teljesség igénye nélkül említsünk meg néhány fejlesztési feladatot. Az utca hálózatra támaszkodva: forgalomirányító lámpák programozása, tömegközlekedési járművek menetrendjének kialakítása (dinamikus allokáció), közúti járművek által okozott légszennyezés eloszlásának vizsgálata, stb. Vízvezeték hálózat esetén a nyomásviszonyok vizsgálata különböző terhelések esetén, mely elemzés eredményei input adatokat szolgáltatnak a hálózat továbbfejlesztését megalapozó tervezéseknek, illetve csőtörések esetén a hibaelhárítás idejére teendő intézkedéseknek. Hasonló feladatokkal találkozunk a gázhálózatban, elektromos hálózatban, stb.

Folyosó tervezés

Míg a hálózatokkal kapcsolatos műveletek egy részét gyakran beépítik a GIS szoftverbe, addig a folyosó tervezési modulok szinte minden esetben felhasználói fejlesztés eredményei. Mivel tehát ezek a függvények nem állnak készen rendelkezésünkre, s ugyanakkor jelentőségük az infrastruktúra fejlődésével valamint a népsűrűség növekedésével egyre nagyobb indokolt, hogy egy kissé részletesebben foglakozzunk a kérdéssel.

A "folyosó" tulajdonképpen a tervezett vonalas létesítmény által szélesebb értelemben lefoglalt földsávot jelenti, melyet kisajátítással vagy szolgalmi joggal a létesítmény üzemben tartója tulajdonba vagy használatba vesz. A sáv szélességét a műtárgy jellege, az építési előírások illetve az építés során végrehajtható tervkorrekciók határozzák meg. Hogy a folyosó kijelölés mennyire éles probléma hazánkban is azt jól mutatták a kelenvölgyi gázvezetékkel kapcsolatos pörlekedések, az elektromos távvezeték építések elleni tiltakozások több Buda környéki községben vagy az M0-ás autópálya nyomvonalának kijelölését követő ellenakciók, melyek Törökbálinttól a budai hegyvidékig terjedtek abban az ütemben, ahogy hozzáláttak az új pályaszakaszok kitűzéséhez.

A tiltakozásoknak ritkán van reális alapjuk, rendszerint egy-két érdekeiben sértett telektulajdonos igyekszik az emberek tájékozatlanságát kihasználva a többséget saját érdekei ellen hangolni. A GIS-hez kapcsolódó tervező modulok gyökereiben képesek megváltoztatni ezt a helyzetet: egyrészt tudományosan megalapozzák a nyomvonal helyzetét, másfelől a GIS által nyújtott szemléltetés meggyőző erővel hat a műszakilag képzetlen emberekre is.

Természetesen a kiválasztott variáns mindig a különböző szempontok kompromisszumát fejezi ki ezért célszerű olyan algoritmusok kidolgozása, melyek többféle kompromisszum alapján többféle variánst dolgoznak ki, lehetőséget biztosítva a közösségek választott képviselőinek a számukra legszimpatikusabb kompromisszum kiválasztására.

A folyosó keresés során a hálózatokkal ellentétben a folyamatos terepen kell megtalálni a kezdő és végpont között azt (azokat) a legjobb útvonala(ka)t, mely(ek) mind a költségek, mind a környezet károsítás minimumát eredményezi(k).

Az eljárás három fő fázist tartalmaz. Az első fázis, mely mind költségben mind időben a legtöbb ráfordítást igényli az adatgyűjtés. A kezdő és végpont kijelölése után a vizsgálati területre általában négyzetcellás raszteres adatokat gyűjtenek. A cella méret a tervezés által megkívánt felbontástól függ, bár az adtok költsége illetve a feldolgozó program lehetőségei is befolyásolják. Tematikus oldalról a létrehozott rétegek függnek a tervezett létesítmény igényeitől, általában olyan rétegeket hoznak létre, melyek tükrözik a műtárgy gazdasági és környezeti hatását, esztétikus megjelenését.
Rendszerint szükség van földhasználati térképekre, talajtérképekre, lejtőkategória térképekre, földtulajdon érték térképekre, vegetációs térképekre, talajvíz térképekre, természetvédelmi térképekre, stb.

A második fázis jelenti a legnehezebb feladatot a tervező számára, mivel ebben a fázisban kell számszerűsíteni minden rétegen az egyes cellák illetve poligonok attribútumainak értékét. Minél nagyobb értéket kap egy cella annál alkalmatlanabb a folyosó létrehozására. Ezután fedésbe hozzák az összes réteget és a kompozit cellák értékét az eredeti rétegek súlyozott kombinációjaként vagy a rájuk alkalmazott logikai műveletek eredményeiként határozzák meg.

A harmadik fázisban a rácsot vagy ritkábban a poligonokat hálózattá alakítják. A poligonok esetében rendszerint először szabályos rácsot hoznak létre a poligonokból, majd a rácsból a hálózatot az eredetileg is raszteres alapú rendszerekkel azonos módon fejlesztik. Ritkábban alkalmazzák azt a megoldást hogy a hálózati pontokat önkényesen veszik fel a poligonok határvonalán.
Az alapesetben tehát a négyzetekből alakítják ki a hálózatot olyképpen, hogy a csomópontokat a négyzetek középpontjába helyezik, és azokat ívekkel összekötik a négy (nyolc) szomszédos négyzet középpontjával. Az ívek attribútumaként annak a cellának az értékét tekintik melyikbe az ív tart (egyes eljárásokban a két cella értékének számtani közepeként számolják az ív attribútumát).
Az így nyert hálózatban aztán megoldják a legrövidebb út algoritmust, azaz meghatározzák azt az utat a kezdő és végpont között, melyen haladva az ívek attribútumainak összege minimális. Ezzel a módszerrel azonban csak egy variánst nyerünk.
Az alternatív variánsok keresésére több módszert is kidolgoztak. Ezek közül egyesek "művi" úton hozzák létre a variánsokat. Ilyen módszer az "iteratív büntető módszer" vagy a "kapukon átmenő legrövidebb utak módszere" [7].
Az első módszer esetébe az optimális út megkeresése után megszorozzák a kapott út íveinek attribútumait egy büntető faktorral és új, második optimális utat keresnek a változatlanul hagyott cellákon, ha több variánsra is szükség van az eljárást többször megismétlik.
A "kapu..." módszer lényege, hogy a kezdő és végpont kivételével minden egyes cellát egy-egy futás során közbenső csomópontnak jelöli ki és az így kapott N-2 variánsból kiválasztja azokat, melyek "hossza" viszonylag alacsony és a köztük lévő terület elég nagy (elég messze vannak egymástól). Valóban új optimális variánst azonban csak akkor kaphatunk, ha megváltoztatjuk a célfüggvényt, azaz a fedvény cellák súlyozási viszonyait a kompozit képzéskor.

Ebben az esetben a közösségek képviselői nem az alapján döntenek, hogy melyik variáns tűnik szebbnek a térképen, hanem azon az alapon, hogy mit tartanak fontosabbnak a pénzkímélést, a környezeti hatásokat vagy az esztétikus megjelenést, s ebben az esetben arról is nyilatkozhatnak, hogy hajlandók e meghatározott pénzt áldozni a környezeti hatások csökkentéséért.