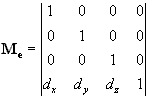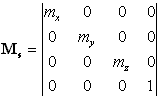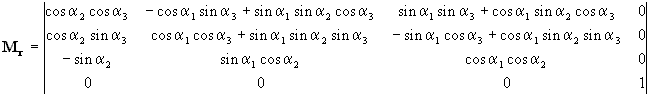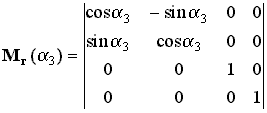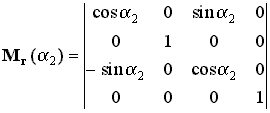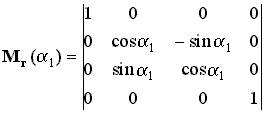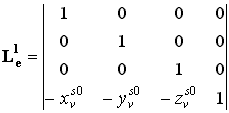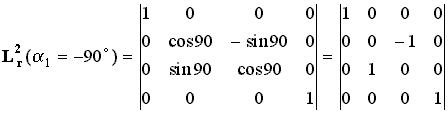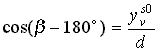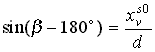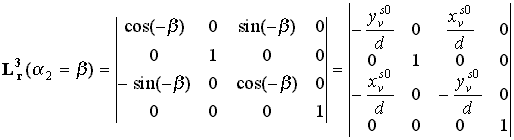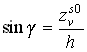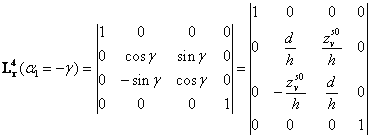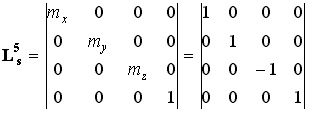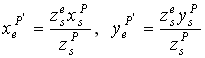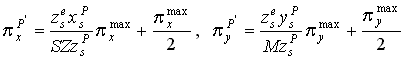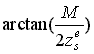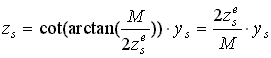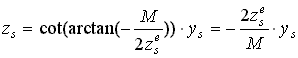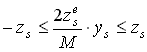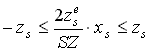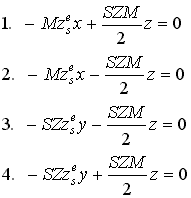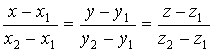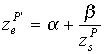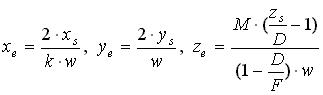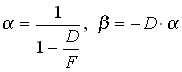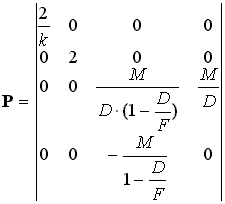Megjelenítési funkciók I

Ezen a lapon a a teljes téma rövid felvázolása után megismerkedünk

a kétdimenziós térképek megjelenítési törvényszerűségeivel, majd rátérünk
a térbeli ábrázolás módszereire, különös figyelmet fordítva
a perspektív ábrázolás törvényszerűségeire.

A Földrajzi Információs Rendszerek egyik funkciója továbbra is a hardcopy térképek előállítása. Ez a funkció azonban kiegészült a megjelenítés képernyős válfajaival, ezen kívül pedig maga a hardcopy is bővült olyan termékekkel, melyeket hagyományos eljárásokkal nem lehetett vagy nem volt gazdaságos tömegméretekben előállítani.

Amint arról az első fejezetben már szóltunk a tárbeli adatbázisok nem számítógépes tárolásának és felhasználásának grafikus eszközei a térképek voltak. Ezek közül is a topográfiai térképek voltak azok a termékek, melyek a maguk technikai szintjén a legjobban hasonlítottak a FIR-ekre. Ezek azok a térképek ugyanis melyek a legtöbb tematikát (réteget) tartalmazzák és pedig nem csak helyzeti, de a lehetőségekhez képest maximális mennyiségű leíró adattal együtt. Ahhoz, hogy a sok adat használható formában jelenjen meg a térkép méretaránya által korlátozott papírlapon a kartográfusok nagy mesterségbeli tudására van szükség. Érdekes jelenség, hogy bár a papírtérképek jelentőségének rohamos csökkenését már sokan és sokszor megjósolták, a legújabb GIS szoftverek népszerűségének mind a mai napig fontos feltétele, hogy rendelkezzenek olyan modulokkal, melyekkel tisztázati térképek eredeti fóliáit lehet készíteni.

A GIS előnye többek közt az, hogy az adatok közül azokat jelenítjük meg, melyekre a kérdéses feladat szempontjából éppen szükségünk van. Ezzel elkerülhetjük a zsúfoltságot és a térképészeti megjelenítés szabályainak automatizálása is egyszerűbbé válik.

A vizsgált tematikák, különösen azok munkaközi állapotának megjelenítő eszköze a képernyő. A képernyő egyik legnagyobb előnye, hogy segítségével szinte korlátlanul használhatjuk a színeket, s lehetőségünk van olyan eszközök igénybevételére is, melyekkel hardcopy-n nem élhetünk (pld. villogó vonalak, területek vagy csak az adatbázis felbontása által korlátozott nagyítás). A képernyő hátrányai közül elsősorban a megjelenített terület viszonylag kis méretét említjük. A nagynak számító 21"-es képernyő átmérője méterben kifejezve 53.3 cm, ha leszámítjuk a kihasználatlan területeket, ez ugyan megfelel egy topográfiai térkép átmérőjének, de arra a képernyőn nincs lehetőség, hogy a térképeket egymásmellé helyezzük és összeragasszuk, amire a gyakorlatban gyakran rákényszerülünk.

Úgy néz ki azonban, hogy ezek a problémák is megoldódnak, akkor ha a kommerciális GIS szoftverek tömegesen fogják alkalmazni a mozgás szimulálás illetve a virtuális realitás lehetőségeit. Ma még ezeket a rendszereket elsősorban repülés szimulátorokban (és játék szoftverekben) alkalmazzák, de GIS alkalmazásuk már 1993 óta napirenden van.

A GIS megjelenítés legnagyobb újdonsága a hagyományos térbeli adathordozókkal (térképekkel) szemben a térbeli ábrázolási lehetőségek tökéletesedésében van.
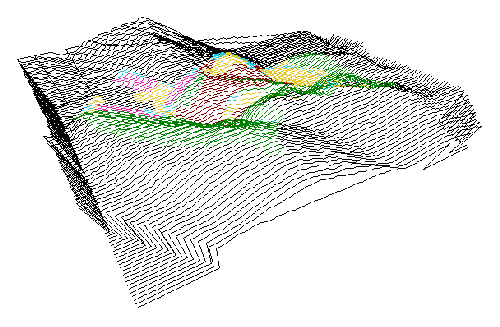
A hagyományos térképek a domborzatot szintvonalakkal mutatták be és drágasága miatt csak kevés országban egészítették ki a topográfiai térképeken a szintvonalakat árnyékolási eljárással. A 80-as évek végétől kezdődően a GIS szoftver termékekbe egyre szervesebben beépültek a DEM vagy TIN modulok, melyek segítségével lehetővé vált a terep perspektív ábrázolása. A perspektív ábrázolás több szoftverben kibővült a tereptárgyak (jelkulcsi elemek) perspektív ábrázolásával, ami megteremtette az animációs megjelenítés feltételeit az adatszerkezet oldaláról.

A továbbiakban megismerünk néhány fontosabb alapelvet és funkciót az ábrázolás területén.

Kétdimenziós térképek megjelenítése

Ahhoz, hogy a térképet használni tudjuk a térképnek rendelkeznie kell kerettel, hálózati vonalakkal és kereten kívüli megírásokkal. A keret a térkép szabványtól függően tartalmazza a kilométer hálózati vonalak és/vagy fokhálózati vonalak megírásait. A keretvonalak rendszerint csak az egyik hálózatot tüntetik fel. A jobb térinformatikai rendszerek rendelkeznek különböző szabványos keretinformációval, de lehetővé teszik a keret egyedi megtervezését is. Tekintettel arra, hogy a GIS szoftverek zöme külföldi eredetű vásárláskor figyelemmel kell lenni arra, hogy az eladók kiegészítették e a szoftvert a magyar szabvány előírásaival. Ez a megjegyzésünk természetesen nem csak a keretre, a szelvénybeosztásra, a kereten kívüli megírásokra, de a globális és lokális referencia felületekre és a jelkulcsra is vonatkozik.

A kereten kívüli megírások (a térkép neve, száma, keletkezési éve, méretarány, jelkulcs, aránymérték, lejtőszög diagramm, szomszédsági diagramm, stb.) általában szintén szabványosak s a program által zömében automatikusan helyeződnek el és töltődnek ki, a jobb szoftverek azonban, éppen a GIS-specifikus termékek megjelentetése érdekében, lehetővé teszik a felhasználó által definiált kereten kívüli megírások létrehozását is.

A hagyományos térképek tervezésének egyik legfontosabb momentuma a feliratok tervezése és elhelyezése. A feliratok nem csak a térképi objektumok nevét közlik a felhasználóval, de utalnak az objektum tájolására, méretére, nagyságára esetleg osztályára. Mindez az elhelyezés, nyújtás, betűtípus és betűnagyság segítségével valósítható meg. A feliratok elhelyezésének szerepét azonnal észrevesszük, ha ránézünk egy térképre: ha az zavaros egyenetlen, olvashatatlan, úgy a feliratok elhelyezésébe hiba csúszott.

A német kartográfus E. Imhof az alábbiakban foglalta össze a felirat elhelyezés legfontosabb szabályait:

A neveknek olvashatóaknak kell lenniük és illeszkedniük kell azokra az objektumokra, melyeket megneveznek;
A név és objektum kapcsolata gyorsan felismerhető legyen;
A nevek nem fedhetik egymást és általában minimális hasznos információt takarjanak ki;
A feliratoknak támogatniuk kell az objektumok tulajdonságainak szemléletessé tételét.

A feltételek teljesítését segíti, ha a nevek elhelyezését fordított sorrendben végzik, mint amilyen a kérdéses felirattípus szabadságfoka.
Először a területi objektumok feliratait helyezik el mivel azoknak nem csak a kérdéses területen belül kell elhelyezkedniük, de kiterjedésükkel le kell fedniük az egész foltot a nélkül, hogy más feliratokkal konfliktusba kerülnének. Ezután kerülhet sor a pontszerű objektumok felirataira, melyeket a pontok közelében kell elhelyezni, végül a legszabadabban elhelyezhető feliratok a vonalas objektumokra kerülnek.

A feliratok elhelyezési szabályainak betartása természetesen nem ennyire fontos, ha kisebb információs tömörségű GIS fedvények, vázlatok, illusztrációk megjelenítése a cél. Ennek megfelelően az eredetileg is GIS-nek tervezett régebbi szoftverek viszonylag kevés lehetőséget biztosítottak a feliratok elhelyezésére, míg az automatikus térképező rendszerekből fejlesztett GIS szoftverek ugyanerre az időre (80-as évek második fele) már gazdag interaktív felirat elhelyezési rutinokkal rendelkeztek, sőt egyesek megkísérelték (egyelőre nem teljes sikerrel) a felirat-elhelyezés automatizálását is. Napjainkban, amint erről már szóltunk a GIS szoftverek kartográfiai képességei rohamosan javulnak, ezért indokolt, hogy új beszerzés esetén ezek minimumának meglétét megköveteljük.

Kívánatos, hogy a szoftver négy szinten támogassa a feliratok elkészítését és elhelyezését.

Az első színt a szabványos színt, itt a térkép szabványnak (és méretaránynak) megfelelő feliratok kerülnek kiválasztásra, automatikus megírásra (az adatbázis alapján) és közelítő elhelyezésre. Az első színt a negyedik, interaktív szinten csak elhelyezésben, kiegészítésben (az adatbázis egyidejű módosításával) és esetleges rövidítés alkalmazásával módosítható.

A második színt nem szabványos, elsősorban térinformatikai termékek előállítását segíti. A felhasználó megadja a térképen ábrázolandó felirat típusok (pld. megyék, települések, vizek, stb.) súlyozását (a típusokon belüli osztályozás a feldolgozás során már elkészült), a készítendő térkép méretarányát és ezek alapján a program megajánlja a betűtípusokat, elkészíti és elhelyezi a feliratokat. A negyedik, interaktív szinten a felhasználó mindent módosíthat.

A harmadik színt jelenti a hagyományos rajzoló programok szintjét, ahol mindent a felhasználó választ és készít a betűnagyságoktól és típusoktól magukig a feliratokig és azok elhelyezéséig.

A negyedik színt az első és második szintek behatárolt módosítására szolgál.

A jelkulcsi elemek (szimbólumok) készítése és elhelyezése a térképkészítés legnagyobb volumenű feladata.

A jelkulcsi elemeket pontszerű, vonalas vagy területi objektumokhoz rendelhetjük. A generalizálással kapcsolatban már említettük, hogy ideális esetben, egy nagyon részletes adatállományból generalizálás segítségével kevésbé részletes, kisebb méretarányban megjeleníthető adatállományt állíthatunk elő. Említettük azt is, hogy a generalizálás nemcsak a vonalak részletgazdagságát hivatott csökkenteni, hanem annak érdekében, hogy a szimbólumok ne fedjék egymást a kevésbé fontos objektumok eltolását vagy megszüntetését is el kell keretében végezni. Ha tehát a kiértékelést pld. ortofotó képernyő digitalizálásával végeztük és azt találjuk, hogy a szimbólumok beillesztése után a vasút és a közút helyenkínt fedik egymást, úgy interaktív módon csak a rajzi állományban a közutat kissé el kell tolnunk, hogy a fedés megszűnjön. A fentiekből következik, hogy bizonyos méretarány alatt interaktív szerkesztésre mindig szükség van.

A szimbólumok esetén és elvárhatjuk a szoftvertől, hogy az adott országban szabványos méretarányok számára szabványos jelkulcsi elemek elhelyezését ajánlja fel. Az elhelyezés módosítása ebben az esetben egyszerűbb lesz mint a feliratok esetében, mivel csak azokat az eseteket kell korrigálni, ahol két vagy több jelkulcsi elem fedésbe kerül, ezen kívül legfeljebb a szimbólum hibás tájolása okozhat gondot.

Térinformatikai elemzések eredményeinek megjelenítésekor, amint már erről szóltunk, általában kisebb a zsúfoltság, ezért lehetőség van nagyobb kifejezőbb szimbólumok alkalmazására is. Ezen kívül a szabványos térképek a területi objektumok jelölésére legfeljebb színes felülnyomást alkalmaznak, míg a térinformatikai rendszerek képesek különböző kitöltő formákkal megkülönböztetni a más és más attribútumokkal jellemzett poligonakat. Végül a GIS olyan tulajdonság együtteseket is tárgyakként kezelhet, melyek a szabványos térképeken nem jelennek meg. Mindezen okok miatt szükség van arra, hogy egy-egy elemzés számára önálló szimbólumokat választhassanak vagy szerkeszthessenek. Támogatandók azok a szoftverek, melyek gazdag előregyártott és méretezhető jelkulcsgyűjteménnyel rendelkeznek (beleértve a kettős vonalak különféle variációit), de e mellett egyszerű eszközöket is nyújtanak egyéni jelkulcsok kialakításához.

Térbeli ábrázolási módszerek

Tulajdonképpen már a magasságmodellezéssel kapcsolatban szólhattunk volna a láthatósági vizsgálatokról. Az, hogy ez a kérdés itt kerül szóba azzal magyarázható, hogy itt viszonylag egyszerű geometriai összefüggésekből levezetett eredményt jelenítünk meg a térképen.

A függvény feladata, hogy kijelölje a térképen azokat a foltokat, melyek egy vagy több pontból (esetleg egy folyamatos útvonalról) az észlelő magasságából szemlélve nem láthatók. Ahhoz, hogy a feladat megoldható legyen szükségünk van a terep digitális magasságmodelljére, az észlelő álláspontjára (pályájára) és annak magasságára, a terepet esetleg borító növényzet magasságára és annak az objektumnak a magasságára amely láthatóságát vizsgáljuk (ha a terep láthatóságára vagyunk kíváncsiak akkor ez a magasság zérus).

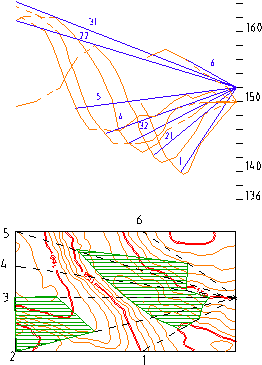
A 4.32 ábrán egy egyszerű példa segítségével kívánjuk megvilágítani a funkció lényegét.

Az ábra alsó részén egy enyhén dombos hazai táj kis részletének szintvonalas ábrázolása látható. A láthatósági vizsgálat segítségével arra keressük a választ, hogy az A ponton álló 2 m. magas szemlélő elől mely terepszakaszok maradnak fedettek.

A vizsgálatot hagyományos szerkesztéssel végeztük, mivel a feladat lényegét így tudjuk egyszerűbben megérteni. E módszer természetesen csak magyarázatra szolgál mivel a GIS szoftver a feladatot pillanatok alatt és sokkal pontosabban el tudja végezni
.

4.32 ábra - láthatósági vizsgálat vázlata

Az ábrán, praktikus okokból (áttekinthetőség, munkaigény) csak 6 irányban vizsgáltuk a láthatóságot, ezért a kapott, be nem látható területek alakja csak viszonylag durva közelítésként fogható fel.

Maga a szerkesztés nem igényel bővebb magyarázatot: az irányok és szintvonalak metszéspontjait felvetítjük a szintvonal magasságát reprezentáló magassági beosztásra, s az egymás utáni pontokat összekötve megkapjuk a kérdéses irány hosszmetszetét - profilját. A profilokat számukkal címkéztük és helyenként hosszú szaggatott vonallal élénkített folyamatos vonallal ábrázoltuk.

Ezután a hosszmetszetben az A pont függőlegesébe felmértük a 2 m. magas szemlélési pontot és e pontból érintő egyeneseket húztunk az egyes szelvényekhez. Az érintési pontokat levetítettük a szelvények alaprajzára és a megfelelő pontokat összekötve megkaptuk a sraffozott kitakart (nem látható) területeket. Talán nem kell ecsetelni, hogy a szoftver nem csak 6 irányban vizsgálja a láthatóságot (és nem a szintvonalakból számítja a metszeteket) s ennek következtében a szoftverrel készült termékeken a kitakart területek határvonalai sokkal tagoltabbak, pontosabbak lesznek.

Lényeges rámutatni, hogy a végeredmény pontosságát szoftver használata esetén is jelentősen befolyásolhatja a terepet borító növényzet magasságának helyes bevitele.

Míg az egy pontból való láthatóságot illetve kitakarást, ha nehezen is, de hagyományos módszerekkel is meg tudjuk határozni, addig a vonalon mozgó álláspontról végzett láthatóság vizsgálatra csak a számítógépi program képes. Bemenő adatként ebben az esetben az út nyomvonalát is meg kell adni.

A perspektív ábrázolás a terepfelszín ábrázolásának leghatásosabb módszere. Ahhoz, hogy a transzformáció lényegét világosan lássuk célszerű, ha felelevenítjük illetve kis mértékben kiegészítjük a síkbeli és térbeli transzformációkkal kapcsolatban ismertetett törvényszerűségeket.

Amint láttuk, alapértelmezésben a grafikai transzformáció azt fejezi ki, hogy adott változtatások (eltolások, méretarány változtatások más szóval skálázások, elforgatások) hatására mik lesznek a pont új helyének koordinátái. Ha a változtatásokat továbbra is M_i-vel jelöljük, ahol az i index a változtatás típusát jelöli (e=eltolás, s=skálázás, r=forgatás), úgy három dimenzió esetén is érvényes, hogy változatlan koordináta rendszerben megadott összetevőkkel elmozdított pont új koordinátáit megkapjuk ha a régi koordináták vektorát megszorozzuk a változási mátrixok szorzatával, azaz

(5).

Az eltolásokat és skálázásokat reprezentáló transzformációs mátrixok viszonylag egyszerűen alakíthatók át három dimenziósokká az alábbiak szerint:

	(6),
	(7).

A forgatási transzformációk mátrixainak felírásához felhasználhatjuk a korábbi eredményeket de figyelembe kell vennünk, hogy homogén koordinátákat használunk, tehát a mátrix dimenzióját bővítenünk kell, illetve azt a tényt, hogy esetünkben nem a koordináta rendszereket mozgatjuk a mozdulatlan pontokhoz képest, hanem a pontokat a mozdulatlan koordináta rendszerhez képest.

4.33 ábra - forgási értelem mozgó pont esetén

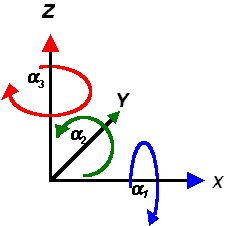
A mozdulatlan pont mozgó pontra cserélését úgy vehetjük figyelembe, hogy megváltoztatjuk a forgatási szögek előjelét vagy ami ezzel egyenértékű a pozitív forgatás irányát. Míg a korábbi esetben az óramutató járásával ellentétes forgást tételeztünk fel pozitívnak, addig a pontok mozgatásához szükséges forgatásoknál az óramutató járásával megegyezőnek tekintjük a pozitív forgatást (4.33 ábra).
Ezzel a "trükkel" elértük, hogy a (8) mátrix zérustól és 1-től különböző elemei megegyeznek a 17.1.1.2 pont R mátrixának értékeivel. Abban az esetben, ha a koordináta tengelyeket kívánjuk elforgatni s a pontokat mozdulatlanul hagyjuk továbbra is érvényes a (8) transzformációs mátrix csak az elfordulás értékeket fordított előjellel kell behelyettesíteni, ami egyenlő azzal, mintha a tengelyek szerinti forgatások pozitív értelmét az óramutató járásával ellenkezőre változtatnánk.

Az M_r mátrix tehát az alábbi alakban írható fel, ha a forgatások sorrendje megegyezik a korábbiakkal, azaz először a Z tengely körül forgatunk -al, majd az Y körül -vel, végül az X körül -el:

(8).

A pont teljes elmozdulását leíró transzformációs mátrix tehát háromdimenziós esetben is az elemi helyzetváltozásokat jellemző transzformációs mátrixok konkatenálásával, egyszerűbben szólva, összeszorzásával nyerhető. Az összeszorzásnál be kell tartani az egyes helyváltoztatások sorrendjét.
Hogy ne legyen problémánk abban az esetben sem, ha a forgatások sorrendje nem egyezik meg a példában szereplővel megadjuk azt a három mátrixot is, melyek az egyes tengelyek szerinti elfordulásokat írják le, továbbra is a 4.33 ábra jelöléseihez tartva magunkat:

	(9),
	(10),
	(11).

Gyakran szükségünk lehet a transzformációk megfordítására. azaz a pont visszamozgatására eredeti helyzetébe. Egyszerűbb esetekben pld. eltolás vagy egy tengely körüli elforgatás esetén kézenfekvő, hogy az inverz transzformációt egy olyan mátrixszal végezhetjük, melyben az eredeti mozgáselem negatív értéke szerepel. Összetett mozgások esetén azonban ez a módszer már nem ad helyes eredményt, ezért ezekben az esetekben az általános matematikai eljárást kell alkalmazni.

Eredményünk azt jelenti, hogy általános esetben az inverz transzformációt az eredeti transzformációs mátrix invertálásával nyert inverz transzformációs mátrixszal kell végrehajtani.

A megjelenítés során a különböző elemi transzformációk sokféle variánsban fordulhatnak elő, gyakran kombinálják a pont mozgástranszformációt a koordináta tengelyek mozgatását leíró transzformációkkal is.

Számunkra, a domborzat térszerű megjelenítése szempontjából a perspektív leképezési transzformációknak van különösen nagy jelentősége, ezért megpróbáljuk röviden e módszer alapelveit is összefoglalni.

A térbeli tárgyakat a hagyományos, mesterséges sztereoszkópiát nem alkalmazó, számítógépek a képernyő síkjára képezik le. Ahhoz hogy a számítógép kitalálja a képernyőn megjelenítendő pontokat arra van szükség, hogy ismerje a tárgy, a szem és a képernyő kölcsönös helyzetét.

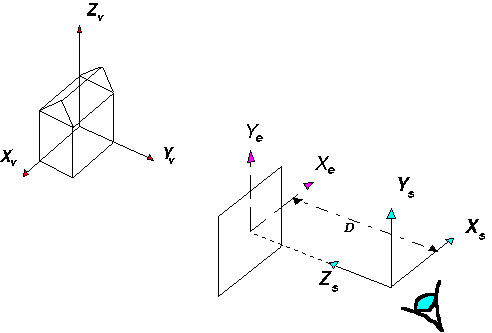
A 4.34 ábra bemutatja a perspektív ábrázolásnál használt koordináta rendszereket.

A szem koordináta rendszer origója a nézőpontban van, Z_s tengelye pedig a tárgy irányába mutat és merőleges a képernyőre. Az X_s és Y_s tengelyek D merőleges távolságra helyezkednek el a képernyő előtt és párhuzamosak a képernyő X_e, Y_e ernyő koordináta rendszer tengelyeivel.

4.34 ábra - a perspektív ábrázolásnál használt koordináta rendszerek

A szemlélt tárgy jellemző pontjai az X_v, Y_v, Z_v úgy nevezett világ-koordináta rendszerben kerülnek megadásra.

Ahhoz, hogy a tárgy képét a képernyőn megjeleníthessük célszerű, ha a tárgyat sarokpontjai felhasználásával áttranszformáljuk a szem koordináta rendszerbe. Ezt a transzformációt leképezési transzformációnak nevezik és általánosságban M_L-el jelölik.

A leképezési transzformációt tehát általánosságban az alábbi kifejezéssel írhatjuk le:

|x_s y_s z_s w|=|x_v y_v z_v w|^.M_L

(12).

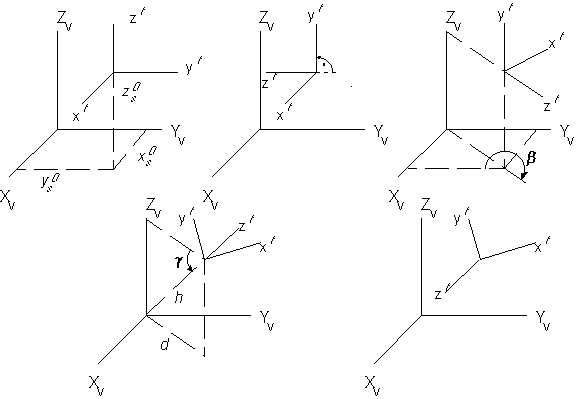
A feladat lényege az M_Lkialakításában van. Nézzük meg röviden milyen lépésekből áll a leképezési transzformáció (4.35 ábra).

4.35 ábra - a leképezési transzformáció lépései

Első lépésként eltoljuk a világ koordináta rendszer kezdőpontját az észlelési pontba. Ha ennek koordinátái a világ koordináta rendszerben x_v^s0,y_v^s0,z_v^s0, úgy behelyettesítve a (6) kifejezésbe:

(13).

Amint a transzformációs mátrixból is látható, koordináta rendszert mozgattunk mozdulatlan tárgypontokhoz képest, ezért az eltolásokat negatív előjellel szerepeltettük (13)-ban.

Második lépésként elforgatjuk a transzformálás alatt álló koordináta rendszert -90^o-al az x^t tengely körül, azaz a (11) mátrixba helyettesítsünk be =+90^o-ot (mivel a koordináta tengelyt mozgatjuk a forgatási szögeket is ellenkező előjellel kell helyettesítenünk):

(14).

A harmadik transzformációs lépésben az y^t tengely körül forgatjuk el a t indexű koordináta rendszert olymódon, hogy a forgatás eredményeképpen a z^t tengely messe a Z_v tengelyt. Az ábra alapján egyszerűen számolható, hogy

és

, ahol

Mivel

, és

a (10) transzformációs mátrix esetünkben a következő alakot nyeri

(15).

A negyedik lépésben az x^t tengely körül forgatunk olymódon, hogy a z^ttengely egyenese átmenjen a világkoordináta rendszer kezdőpontján.

Az ábra alapján

és

, ahol

Mivel és a (11) típusú transzformációs mátrixot esetünkre a következő alakban írjuk fel:

(16).

Utolsó transzformációnk a z^t tengely irányának megfordítását célozza, mivel az eredményül kapott szem-koordináta rendszer pozitív z tengelye mindig a szemlélt tárgy irányába mutat. E forgatást olyan (7) típusú skálázó mátrixszal végezhetjük, melynek z irányú skála faktora -1. A fentiek szerint nyert mátrix a következő:

(17).

A szemlét tárgy jellemző pontjainak koordinátáit, melyeket eddig csak a világkoordináta rendszerben ismertünk, a transzformációs mátrixok segítségével az alábbi formulával képezhetjük le a szem-koordinátarendszerbe:

|x_sy_sz_sw| = |x_vy_vz_vw| ^. L¹_e ^. L²_r ^. L³_r ^. L⁴_r ^. L⁵_s

(18).

A leképezési transzformáció után a perspektív transzformáció már egyszerűen végrehajtható, mivel nem kell mást tennünk, mint a szemkoordináta rendszerből kiinduló vetítősugarakkal rávetíteni a tárgy jellemző pontjait a képernyőre, azaz meghatározni a vetítősugarak metszéspontjainak képernyő koordinátáit. Rögtön meg kell jegyeznünk, hogy egyelőre csak a felület, illetve test drótvázának perspektív ábrázolásával foglalkozunk.

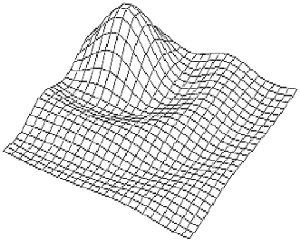
4.36 ábra - szabályos felület drótvázas perspektív képe

Szabályos testek esetén a drótvázat a test élei alkorják. Felületek esetén a felületre illesztett, alaprajzban szabályos vagy szabálytalan hálóval helyettesíthetjük a drótvázat. Rögtön megjegyezzük, hogy amint azt a 4.36 ábra is bizonyítja, megfelelő nézőpont megválasztása esetén a szabályos rácsháló kielégítően tükrözi a terep domborzatát.

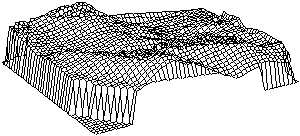
A 4.36 ábrán gondoskodtunk arról is, hogy a láthatatlan vonalak ne jelenjenek meg a képen. Hogy ez mennyire zavaró lehet azt a 4.37 ábra drótvázas domborzatábrázolása bizonyítja. A képet az OSUMAP oktatásra készített GIS szoftver 'SURFACE' (felület) parancsával készítettük, majd raszter-vektor átalakítással csökkentettük a fájl méretét, a transzformáció azonban, feltehetőleg a rendszer durva pixelfelbontása következtében, az ábra hátsó részén láthatóan nem teljesen birkózott meg a problémával.

4.37 ábra - terep felszín drótvázas perspektív képe

A dróthálós domborzatmegjelenítés valóság kifejező hatása tovább javítható ha a domborzat perspektív képére rávetítjük valamely tematikus fedvény képét.

4.38 ábra - terep felszín drótvázas perspektív képére vetített földhasználati réteg

Mivel továbbra is vonalakkal ábrázoljuk a felszínt, a rávetítés úgy történik, hogy azok a vonalszakaszok, melyek valamely területi objektum belsejében haladnak felveszik a kérdéses területi objektum megjelenítésére használt színt. A 4.38 ábrán a 4.37 ábrán már bemutatott domborzatra rávetítettük a vizsgált terület növényzetét tartalmazó fedvényt. A műveletet az OSUMAP 'DRAPE' elnevezésű utasításával végeztük.

A sík vetületben párhuzamos vonalak a terepmagasságok hatására vonalanként összefüggő háromdimenziós egyenes sereggé változnak. A fedvény illesztés következtében az egyenesek száma tovább nő, mivel ugyanannak az egyenesnek két különböző tematikus foltba eső szakaszait a különböző színezés miatt külön kell kezelni. A foltokkal való metszéspontokat a program célszerűen még a síkvetületben meghatározza, majd az egyenesek térbelivé tétele után számítja a kérdéses síkkoordinátákhoz tartozó magassági információt. A drótháló perspektív ábrázolásának számításához tehát végpontjaikkal megadott egyenes szakaszok állnak rendelkezésünkre.

Első feladatként a programok a magasságok és folt metszéspontok figyelembe vételével kiszámítják az egyenes szakasz végpontok világ koordinátáit, majd második lépésben a (18) transzformáció segítségével ugyanezen pontok szemkoordinátáit. A későbbi összekötési információ rögzítését már a transzformáció előtt el lehet végezni, mivel az összekötendő egyenes szakaszok végpontjainak jelölése a transzformációk után sem változik. Harmadik lépésben történik a pontok rávetítése a képernyőre, azaz a tulajdonképpeni perspektív transzformáció.

A 4. 39 ábrán függőleges (vagy vízszintes) síkra vetítjük a P(x_s,y_s,z_s) szem koordináta rendszerben megadott pontot a szem koordináta rendszer kezdőpontjával összekötő egyenes (azaz a perspektív vetítősugár) képét. Ha a képernyő szem koordináta rendszerben kifejezett z koordinátáját (azaz a képernyő merőleges távolságát a szemponttól) z_s^e-vel jelöljük, úgy a kérdéses pont képernyő koordinátáit a következő kifejezésekből számíthatjuk:

(19).

4.39 ábra - a perspektív vetítősugár képe a függőleges síkon

Mivel a transzformáció eredményeit a képernyőn kívánjuk megjeleníteni célszerű az e indexű metrikus koordinátákat a képernyő koordináta rendszer pixelben kifejezett koordinátáiba átalakítani. Jelöljük a képernyő magasságát M-el, szélességét SZ-el, tételezzük fel, hogy a képernyő bal alsó sarkának mindkét pixelkoordinátája 0, a jobb felső sarok pixelértékei pedig , akkor a vizsgált P^' pont pixelben kifejezett képernyő koordinátáit az alábbi kifejezések szolgáltatják:

(20).

A drótvázat térbeli egyenesek alkotják, melyek perspektív vetületei is egyenesek. Ha az egyenesek végpontjait a (20) szerint a képernyőre vetítjük, úgy a képernyőre vetített pontokat összekötve megkapjuk perspektív vetületüket. Ez azonban csak akkor igaz, ha a kérdéses pontok a vetítési gúlán belül helyezkednek el (4.40 ábra a részlet).
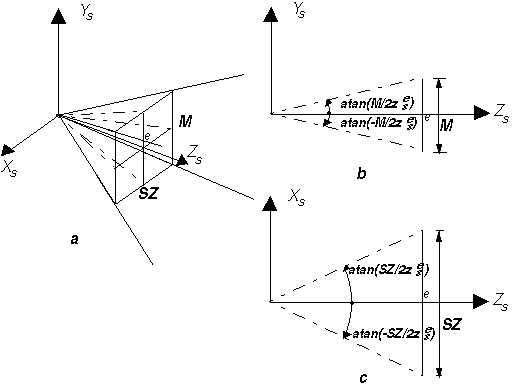
Készítsük el a vetítési gúla metszetét az Y_sZ_s síkkal (4.40 ábra b részlet). A gúla felső és alsó alkotójának szöge a Z_s

tengellyel

, azaz a felső alkotón elhelyezkedő pontokra felírható, hogy

Hasonló meggondolásokból kiindulva az alsó alkotón elhelyezkedő pontokra igaz, hogy

. Ezek szerint annak egyik feltétele, hogy a

pontok a vetítési gúlán belül helyezkedjenek el az, hogy

(21).

Ha elkészítjük a vetítési gúla metszetét az X_sZ_s síkkal (4.40 ábra c részlet), úgy egyszerűen belátható, hogy azok a pontok lesznek a vetítési gúlán belül, melyekre fennáll a

(22)

feltétel.

4.40 ábra - a vetítési gúla geometriája

A fenti meggondolások alapján tehát a (21) és (22) segítségével kiválaszthatjuk azokat a pontokat, amelyek a vetítési gúlán belül vannak, tehát a képernyőn megjelenítendők.
Nem ilyen egyszerű azonban a helyzet az egyenesekkel. Mielőtt ezek részletesebb vizsgálatára rátérnénk nem szabad elfelejtenünk, hogy egyenes szakaszokkal és nem végtelen hosszú egyenesekkel van dolgunk.

Első lépésben megvizsgáljuk a (21) és (22) segítségével, hogy az egyenes végpontjai belül vannak-e a vetítési gúlán vagy sem. Három eset lehetséges:

Mindkét pont a gúlán belül van. Ebben az esetben levetítjük a pontokat a képernyőre és vetületük összekötésével nyerjük a vonal perspektív képét.
Az egyik végpont a gúlán belül van, míg a másik végpont a gúlán kívül. Ebben az esetben biztosak lehetünk, hogy az egyenes szakasz egy részének lesz perspektív képe a képernyőn. Azt a műveletet, mely az egyenes szakasz egy részét leválasztja vágásnak nevezzük.
Mindkét végpont a gúlán kívül található. Ez a feltétel nem zárja ki csak lehetővé teszi, hogy az egyenesnek ne legyen perspektív képe a képernyőn.

A 3. eset megoldási lehetőségeit a 4.41 ábrán vázoltuk fel.

4.41 ábra - a vetítési gúlán kívüli végpontok esete

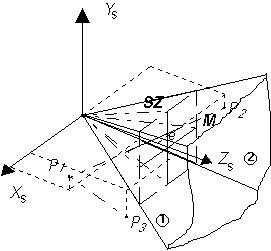
Ahhoz, hogy a vágást akár a második, akár a harmadik esetben el tudjuk végezni meg kell határoznunk a vágási gúlát alkotó síkok egyenleteit. Ha a függőleges síkokat az ábra szerint 1-el és 2-vel, a vízszintes síkok közül a felsőt 3-al, az alsót 4-el jelöljük (a vízszíntes síkok jelölését a zsúfoltság csökkentése miatt az ábrán elhagytuk), úgy egyenleteik az alábbi alakot nyerik:

(23).

A két pontjával adott egyenes egyenletrendszerét az analitikus geometria az alábbi alakban adja meg:

(24),

ahol az 1,2 indexek az első és második pontot jelölik.

A 2. esetben, tehát amikor az egyik pont a gúlán belül, a második pedig azon kívül van a (23) és (24) egyenletek felhasználásával kiszámíthatjuk az egyenes metszéspontjait a síkokkal.

A (24) rendszer azonban nem egyenes szakaszokat hanem végtelen hosszú egyeneseket ír le, a (23) egyenletek pedig szintén tetszés szerinti értékeket vehetnek fel y illetve x értelemben.

Ezért kétféle probléma is felmerül: a gúlán belüli pontból kiindulva az egyenes nem csak a másik adott pont irányába, hanem az ellenkező irányban is metszi a gúlát, másfelől az egyenes a gúlán kívül is metszi a gúlát alkotó síkok valamelyikét. A problémákat a 4.42 ábrán a Z tengelyre merőleges metszetben próbáltuk érzékeltetni.

4.42 ábra - a vetítési gúlán kívüli és belüli végpontok esete

A metszéspontok kiszámítása után először azt kell eldöntenünk, hogy a pontok az egyenes szakaszon belül vannak-e. Ezt egyszerűen úgy dönthetjük el hogy metszéspontonként megnézzük, hogy a kérdéses i-edik metszéspont valamelyik koordinátája a végpontok megfelelő koordinátái által határolt szakaszra esik-e, azaz az i-edik metszéspont a P₁,P₂ egyenes szakaszon van ha a

(25)

egyenlőtlenség teljesül.

A szakaszon lévő metszéspontok közül ezután a (21) és (22) kifejezések segítségével kiválasztjuk azokat, melyek a gúlán helyezkednek el, majd a (20) kifejezés felhasználásával nyerjük a képernyőn a látható egyenes szakaszvégpontok képkoordinátáit, melyek összekötésével kapjuk a drótvázat alkotó egyenes darabokat.

A gyakorlatban nagyon zavaró lehet, ha a látható és láthatatlan vonalak egyaránt leképződnek a képernyőn. Gondoljunk arra, hogy hagyományos grafika esetén is igyekszünk szaggatott vonallal megkülönböztetni a nem látható éleket.

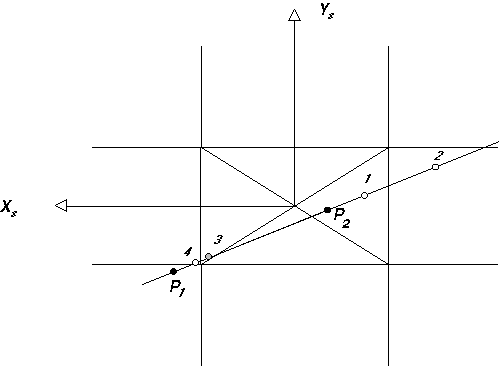
A 4.43 ábrán három pontot vetítettünk képernyőre. Mivel a pontok egy vetítő sugáron helyezkednek el mindhárom pont a képernyő ugyanazon a helyén jelenik meg. Az hogy közülük melyik látható attól függ, hogy melyik van a legközelebb a képernyőhöz. Ezt a közelséget a z_s értékkel is kifejezhetnénk, de ebben az esetben a vizsgálatokat (beleértve két pontot összekötő egyenes vizsgálatát is) különböző hajlásszögű ferde vetítősugarakon kellene végezni.

Sokkal egyszerűbb az ernyő koordináta rendszer kibővítése a Z_e tengellyel, mivel ebben az esetben a képsíkra merőleges vetítősugarak mentén kell a távolságokat meghatározni. Az ernyő koordinátarendszer kibővítése alatt egy olyan transzformációt értünk, mely eredményeképpen a transzformált pont x és y koordinátáját továbbra is a (19) kifejezésekből nyerjük. A pont ernyő koordináta rendszerben kifejezett z koordinátáját abból a feltételezésből kiindulva nyerjük, hogy a szemkoordináta rendszerben lévő síkok az ernyő koordináta rendszerben is síkokká transzformálódjanak. 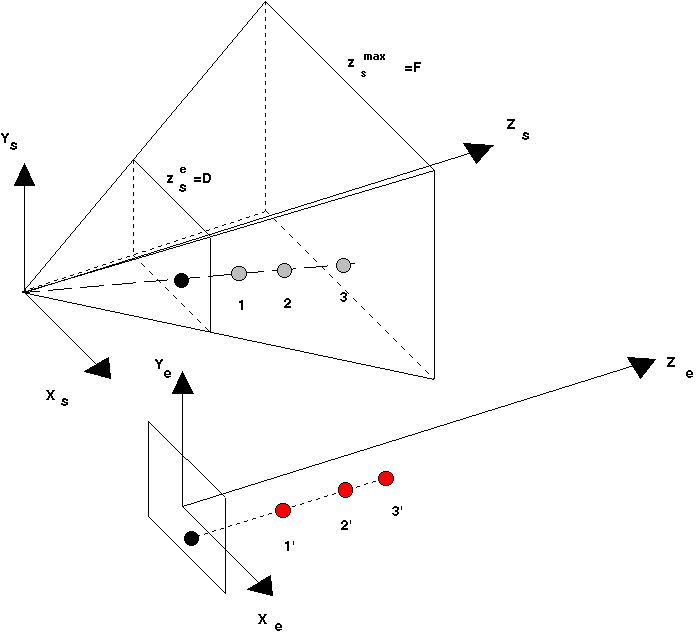Igazolható, hogy ez elérhető, ha a transzformált z koordináta kielégíti az alábbi kifejezést:

(26).

4.43 ábra - az ernyő koordináta rendszer kibővítése Z tengellyel

Az és megválasztásánál abból az elvi meggondolásból kiindulva, hogy a szemkoordináta rendszerben nagyobb z-nek az ernyő koordináta rendszerben is nagyobb z feleljen meg, előjelét negatívnak kell vennünk, egyébként értéküket praktikus meggondolásból vezetjük le. Azt akarjuk ugyanis elérni, hogy z_e értéke csak a intervallumra legyen meghatározott, mégpedig olymódon, hogy az alsó határon 0, a felső határon 1 értéket vegyen fel. Ez az értéktartomány összhangban van az x_e,y_e (19)-ben értelmezett -1, +1 értéktartományaival. A teljes perspektív transzformációt felírhatjuk a homogén koordinátákkal is az alábbiak szerint:

Legyen		a képernyő szélességének és magasságának viszonya és		,

akkor

(27).

Nem nehéz kimutatni, hogy a (27)-ben a (26) szabad paramétereit a következő értékekkel vettük figyelembe:

A (27) kifejezést egyszerűbben számíthatjuk, ha a műveleteket egy vektor-mátrix szorzásra majd az azt követő osztásokra redukáljuk:

		(28)
		(29)
		(30).

A vágási határokat az osztás előtti koordináták felhasználásával az alábbi egyenlőtlenségek szolgáltatják:

(31).

Mivel a feltételezésünk szerint a leképződő pontok z_e koordinátái 0 és 1 közé esnek, a leképezésből z értelemben kieső pontok vágására a

(32)

egyenlőtlenséget használjuk. Nem igényel további magyarázatot, hogy azokra az esetekre, amikor az egyenes szakasz nem mindkét végpontja kerül leképezésre a (23), (24), (25) kifejezések továbbra is használhatók, de lehetőségünk van arra is, hogy e kifejezéseket is átírjuk a w-vel történő osztás előtti, index nélküli koordináta rendszerbe.

Az elmondottak alapján meg tudjuk határozni, hogy azonos x_e,y_e képernyő koordinátájú pontok közül melyik látszik, az igazi probléma azonban az, hogy a síklapok miként takarják a többi geometriai elemet.

A megoldásnak különböző lehetőségei vannak. Ismertek geometriai megoldások, melyek a testet határoló síkidomok (sokszögek) kölcsönös helyzetét vizsgálják.

A vizsgálat első lépésében kiválasztják a hátsó határoló lapokat alkotó sokszögeket, (azokat, melyek ax_e+by_e+cz_e=0 egyenletében c>0), majd ezeket egyelőre figyelmen kívül hagyva kiválasztják azokat a sokszögeket, melyek a képernyő síkjában nem metszhetik egymást mivel az egyik legkisebb x vagy y koordinátája nagyobb mint a másik legnagyobb x vagy y koordinátája. Ha az analóg vizsgálatot elvégezzük a z koordinátákra is, úgy ki tudjuk választani azokat a sokszöglap párokat, melyek egymást az ernyőkoordináta rendszerben nem metszik, s melyek közül a nagyobb z-vel rendelkező az előtte lévőt nem takarhatja. További vizsgálatot igényelnek azok a sík sokszöglapok, melyek a képernyő koordináta rendszerben ténylegesen metszik egymást, mivel ezek a párok mindkét eleme takarhat valamit a másikból.

A geometriai elveken működő algoritmusok lényege tehát abból áll, hogy rendezéssel kiválasztják a problémamentes eseteket és a részletes vizsgálatot csak a bonyolultabb esetekre alkalmazzák. Tulajdonképpen ezek a módszerek nem mások mint a 10.3 pontban az egyenes szakaszok metszésével kapcsolatban bemutatott síkbeli algoritmusok térbeli kiterjesztései. Különösen előnyös a geometriai megközelítés konvex poliéderek esetén, ugyanis igazolható, hogy ha e testek valamelyik lapjának egyik része látszik, úgy az egész lap látszik. Természetesen a tétel fordítottja is igaz.

A számítógépek memória kapacitásának és műveleti sebességének rohamos növekedésével párhuzamosan nő a kevésbé kifinomult szisztematikus módszerek térhódítása. Ilyen módszernek nevezhető a korreláció nélküli mélységpuffer algoritmus.

Első lépésként rendeljünk minden sík sokszöglaphoz egy intenzitás vagy színértéket. A következő lépésben deklarálunk két mátrixot, melyek elemszáma megegyezik a képmátrix pixel számával: , ezek a mátrixok fogják tárolni a látható pontok z értékeit, illetve egy kérdéses z-hez tartozó síklap intenzitását vagy színét.
A feladatunk az lesz, hogy minden pixelre a neki megfelelő x,y értékek felhasználásával kiszámítsuk az összes olyan sík sokszöglap z koordinátáját, amelynek van ilyen x,y koordinátájú pontja, és -nek a kezdeti 1 érték után akkor adunk újabb z értékét, ha a következő poligon megfelelő pontjához kisebb z érték tartozik. Az aktuális Z_ij értéknek megfelelően átállítjuk értékét is a háttérnek megfelelő kezdeti értékéről és végeredményképpen egy olyan mátrixot kapunk, mely tartalmazza valamennyi képpont szürkeségi értékét vagy színét.
Talán az algoritmus rövid felvázolása alapján is belátható, hogy a módszer tárolási igénye jelentős (valamennyi sík sokszöglap egyenletét tárolni kell), de a műveleti igény sem jelentéktelen, hisz minden képpontban meg kell vizsgálni valamennyi sokszöglapot. A fenti hátrányok csökkentésére sokféle módszert dolgoztak ki, ezek tárgyalása azonban túlnő könyvünk keretein. Az érdeklődők a [8] és [9] monográfiákban találhatnak további részleteket.

Az elmondott eljárások közvetlenül jól használhatók a 3D-s rajzoló (CAD) szoftverekben, de továbbfejlesztésre szorulnak ahhoz, hogy eredményesen alkalmazhatók legyenek a szabálytalan felületek térbeli ábrázolásakor. A bevezetőben már láttunk arra példát, hogy a terepfelszín térbeli ábrázolásának egyik eszköze az lehet, ha a felszínre vízszíntes vetületben szabályos vonalhálózatot fektetünk, majd a vonalakat a DTM segítségével egyenes szakaszokból álló térbeli sokszögekké alakítjuk és képezzük ezek perspektív képét.