Alapműveletek vektoros és raszteres térbeli adatokkal I
Ebben a részben megismerkedünk:
- A raszter-vektor átalakítással, ezen belül
- a korrekt mintavételezés feltételeivel (kompatibilitási feltételekkel) ,
- az idomok határvonalának megkeresésével,
- vékony objektumok tengelyvonalainak meghatározásával (objektumvékonyítással),
- a bináris váz vektorizálásával, az iveket alkotó pontok ritkításával;
- a vektor-raszter konverzióval.
A térinformációs rendszerek szoftverjei a térbeli adatokkal különböző műveleteket hajtanak végre. A műveletek egy jelentős részénél az alfanumerikus illetve grafikus adatbázisokkal kapcsolatban már megismert lekérdezési mechanizmusok egyszerű vagy összetett alkalmazásairól van szó. Más feladatok ugyanakkor olyan geometriai illetve halmazműveletek végrehajtását igénylik, melyekről a téma kapcsán még nem szóltunk. Ezeket az alapfeladatokat a továbbiakban összhangban az angol és német terminologiával műveleti alapeszközöknek fogjuk hívni.
Mielőtt azonban az alapeszközök tárgyalására rátérnénk külön pontban foglalkoznunk kell a raszter - vektor, vektor - raszter átalakítás témakörével. A nyolcvanas évek végéig a témát elsősorban a szkannolással és digitális fotogrammetriával kapcsolatban tárgyalták (ezekre a kérdésekre a harmadik fejezetben térünk ki). Napjainkban azonban egyre jelentősebb szerepet játszik a hybrid adatmodellű GIS szoftver koncepció, mely korrekt, egyértelmű raszter - vektor, vektor - raszter konverziók nélkül nem képzelhető el. Ennek a koncepciónak az a lényege, hogy a térbeli mőveleteket mindíg olyan modellben kell végrehajtani amelyikben egyszerűbb. Példaképpen megemlíthetjük, hogy a fedvénymetszési műveletek (overlay) a raszteres adatmodellel igen egyszerűen végezhetők, mig a vektormodellben igen sok számítást és rendezést igényelnek, a távolság és kerületszámítások ugyanakkor, pontosan és egyszerűen csak a vektoros adatmodellben hajthatók végre.
A vektoros adatmodell minden esetben erősebb általánosítás (generalizálás) eredménye mint a raszteres modell. Következésképpen az semmilyen konverziótól sem várható el, hogy a vektor modellből helyreállítsa az eredeti raszteres állományt. Az azonban igen, hogy ha egy vektoros modellben tárolt poligont átalakítunk raszteres alakba, majd az így nyert raszterképet vissza konvertáljuk vektoros adatokká a kiindulóval azonos poligont nyerjünk. A fentiekből az is következik, hogy a vegyes adatmodellű GIS-ekben a képi (tehát nem térképi) eredetű raszteres adatokat célszerű eredeti formátumukban is tárolni.
Raszteres adatmodell átalakítása vektoros adatmodellé (raszter-vektor konverzió)
Raszteres adatok digitális kamarákkal történő fényképezés, mesterséges holdakról történő szkenneres felvételek, fényképek és térképek vagy rajzok szkennelése (letapogatása) útján jöhetnek létre. A digitális kamarák, a fényképek szkennelése és a fényképszerű szkennelés tónusos raszteres adatmodellt eredményez, ami számítástechnikailag azt jelenti, hogy minden egyes képelem (pixel) egyedi, adott határok közötti (egy vagy két byte-al leirható) attribútummal, úgy nevezett szürkeségi értékkel rendelkezik. A szkennelt térképek illetve rajzok rendszerint bináris képet szolgáltatnak, azaz a letapogatott rajzi tartalom feketének, a háttér fehérnek tekinthető és egy bit két értékével (0,1) jellemezhető. A tónusos képekkel végzendő egyes műveletekre valamint arra a technológiára, amely a szkennelés eredményeként létrejött zajos képekből szűrt bináris képeket állít elő a harmadik fejezetben még visszatérünk. A jelen pontban a jobb érthetőség kedvéért kizárólag bináris raszterképek vektorokká alakításával foglalkozunk.
A korrekt mintavételezés feltételei (kompatibilitási feltételek)
Az analóg képek pixelekre bontása (diszkretizálása) alapfeltétele a számítógépes grafika s ezen túl a számítógépes alakfelismerés alkalmazhatóságának. Ez utóbbi feladatok alapkérdéseivel foglakozik Pavlidis alapvető, 1982-ben megjelent monográfiája [7]. E könyv eredményeit felhasználva igyekszünk bizonyítások nélkül összefoglalni a diszkretizálással, ezen belül, a raszter-vektor, vektor-raszter átalakítással kapcsolatos alapkérdéseket.
Mindenek előtt a szomszédság fogalmának bevezetésével kell foglalkoznunk. Erre azért van szükségünk, mert valamilyen megfelelést kell találnunk az analóg képen plauzibilis szomszédsági fogalomnak a pixelek világában.
|
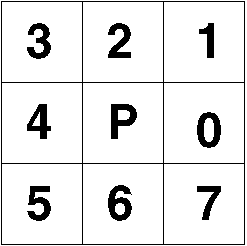
A 2.27 ábrán kilenc pixelt ábrázoltunk. A kérdéses (figyelembe vett) pixelt P-el jelöltük, míg a mátrix többi elemét 0-7-ig terjedő nyolc számjeggyel. Jelöljük e számjegyeket N-el, és nevezzük el a P-t körülvevő pixeleket a P-re vonatkozó N-szomszédoknak. E szomszédok között különbséget tehetünk a szerint, hogy N páros vagy páratlan. Páros N esetén a két pixel egy oldal mentén találkozik ezt a szomsédságot d(irekt)-szomszédságnak míg a páratlan N-el jelölt pixelek elhelyezkedését, melyek csak egy sarokponton találkoznak P-el i(ndirekt)-szomszédságnak nevezzük. |
A szomszédság fogalom felhasználásával a
pixelek bejárásához különböző típusú utakat határozhatunk meg. Ha nem kötjük
meg, hogy az egymást a bejárás során követő pixelek milyen típusú
szomszédságban legyenek csak azt, hogy szomszédok legyenek úgy i-útról
vagy egyszerűen csak útról beszélünk. Ha a bejárás egymás után következő
elemei d-szomszédok, úgy d-útról beszélünk. Egyszerű út
esetén a sorozat valamennyi pixele egyedi és nincs az úton belül kettőnél több d-szomszédja.
Zárt út esetén az első és utolsó pixel egybeesik.
Lényeges szerepet játszik az alakzatok leírásában az összekapcsoltság fogalma. Azt mondjuk, hogy egy S pixelhalmaz összekapcsolt ( vagy i-kapcsolt), ha minden C és D pixelpárjához tartozik egy olya i-út, melynek kezdő és vég eleme C és D és az összes többi eleme S része. Ha a kérdéses pontok d-úttal kapcsolhatók össze, úgy a pixelhalmazt d-kapcsoltnak nevezzük.
Ahhoz, hogy az analóg képet a diszkrét (pixeles) kép kielégítően ábrázolja szükséges hogy a két kép topológiailag egyenértékű legyen. A topológiai egyenértékűség, amint arról már szóltunk, népszerűen fogalmazva azt jelenti, hogy a két alakzat nyújtással és zsugorítással szakadás és vágás nélkül átvihető egymásba.
|
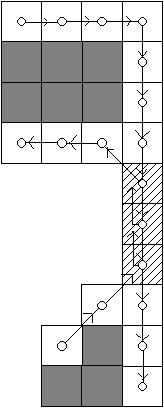
A 2.28-as ábrán bemutatunk egy eredeti képet, és az ábrán látható pixelmérettel történő letapogatással nyert diszkrét képét. Igazolható, hogy a két kép topológiailag ekvivalens, mégis egyszerű szemlélet alapján megállapíthatjuk, hogy a raszteres kép hasonlósága az eredeti képhez a legtöbb gyakorlati feladat szempontjából nem kielégítő. |
|
Ahhoz, hogy a topológia mellett az
eredeti kép alakját is megőrizzük jelentős mértékben csökkentenünk kell a
diszkrét kép pixel méretét, vagy ami ezzel egyenértékű, növelnünk kell a
letapogatás felbontását.
A fenti követelmények (topológia és
alak) akkor teljesíthetőek, ha a letapogató háló lukbősége h kompatibilis
az analóg képpel. A kompatibilitásnak az a feltétele, hogy létezzen egy olyan
távolság, mellyel alkotott C kör valamennyi R fekete tartomány
valamennyi határpontjához érintőként simul és teljes egészében benne van R-ben.
Ugyanez érvényes R kiegészítőjére is.
A fenti szigorú megfogalmazás gyakorlatilag azt jelenti, hogy minél nagyobb a fekete (illetve fehér) folt határának lokális görbülete, annál kisebb kell hogy legyen a raszter hálóbősége. Ne felejtsük el, hogy a kompatibilitás szempontjából mértékadónak valamennyi folt valamennyi határpontja közül a legnagyobb görbületű tekintendő.
Kétségtelen, hogy a kompatibilitási feltétel szigorú megkötéseket tartalmaz a foltok szélességére s határvonalaik görbületére. Térinformatikai szempontból különösen érzékeny megkötés, hogy nem engedi meg a sarkokat. A gyakorlatban ezen a nehézségen úgy tehetjük túl magunkat, hogy a sarkokat olyan kis ívekkel helyettesítjük, melyek az igényelt felbontásban nem érzékelhetőek. Sajnos ez a megoldás különösen kataszteri térképek szkannolásakor gazdaságosan nem érvényesíthető. Ezért találunk e térképek raszteres változatain következetesen íves telekhatár pontokat. Mivel a pixelméret túlzott csökkentése napjainkban még gazdasági szempontból nem engedhető meg a keletkezett hibát a vektorizálási folyamatban szakértői modulok alkalmazásával próbálják megszüntetni.
Figyelemre méltó a felbontóképesség meghatározása azokban a gyakorlati esetekben is amikor vektoros adatokat akarunk számszerűleg (billentyűzetről vagy kézi digitalizálással) raszteres rendszerekbe bevinni. Megfelelő eredményt csak akkor érhetünk el, ha a raszteres rendszer alapszoftverje lehetővé teszi h beállítását a kompatibilitási követelményeknek megfelelően.
Összefoglalva megállapítható, hogy a kompatibilitás megléte biztosítja az analóg kép topológiájánk megőrzését a diszkrét képben, s egyben biztosítja az alak megtartását is. Ez utóbbival kapcsolatban figyelemreméltó az a bizonyítható megállapítás, hogy ebben az esetben az analóg és a diszkrét kép két megfelelő pontjának távolsága nem lehet nagyobb mint d.
Az idomok határvonalának megkeresése
A szkennelt kép kisebb nagyobb kiterjedésű objektumokból áll. A vektoros adatmodell ugyanakkor elméleti vonalakból építi fel objektumait. A térképek különösen a kataszteri térképek látszólag szintén csak vonalakból állnak. Ha célunk a raszteres modellből vektoros modellt előállítani, úgy meg kell különböztetnünk a szkennelt kép kisebb nagyobb objektumai közül azokat, melyek valóban területet kívánnak modellezni azoktól, melyek tulajdonképpen vonalak és csak azért tűnnek területnek mivel az analóg térképen nem lehet elméleti vonalat rajzolni, illetve olyan vonalas létesítmények, melyeket a térképen szélességi kiterjedéssel is rendelkező egyezményes jelekkel ábrázolunk, információs rendszerünkben azonban geometriai adatként csak tengelyvonalukat kívánjuk tárolni, szélességüket egyéb tulajdonság jellemzőikkel együtt külön adatbázisban szerepeltetjük.
A kétféle adattípust a képfeldolgozási irodalom is megkülönbözteti: vastag régióknak és vékony vonalaknak nevezi őket. Bármelyik adattípust is kívánjuk azonban feldolgozni mindenek előtt meg kell határoznunk az objektum körvonalát (kontúrját).
Egy összetett objektum több belső szigetet is tartalmazhat. Mielőtt rátérnénk e szigetek kontúrjainak meghatározására foglalkozzunk az objektum egészét határoló körvonal meghatározásával. Az algoritmusnak, mint általában, csak az alapgondolatát közöljük a részletek iránt érdeklődőknek a [7] 7. fejezetét alánjuk figyelmébe.
Függőleges vagy vízszintes letapogatással keressük meg az első pixelt, melynek 4 irányú (a 2.27 ábra kódolása szerint) szomszédja nem tagja a halmaznak. Mivel bináris képekről van szó ez azt jelenti hogy keresünk egy olyan 1 értékű (tehát fekete) pixelt, melynek keleti (4 irányú) szomszédja 0 értékű (tehát fehér). A kiinduló pont megtalálása után megkeressük a következő pixelt olymódon, hogy az a körbejárás haladási értelmétől leginkább jobb kéz felé helyezkedjen el. Ezt az algoritmus úgy éri el, hogy az S iránykódot a kezdeti 4-es értékből kiindulva szisztematikusan úgy változtatja, hogy az első vizsgálandó pixel mindig a haladásnak megfelelő még elképzelhető legjobboldalibb pixel legyen.
A fentieknek megfelelően az iránykódok a következőképpen változnak: legyen S kiinduló értéke 6, az első keresést az S-1=5 irányba tehát a kiinduló pontból lehetséges első irányba végezzük mivel a 4-es irányban, feltételeink szerint, nem lehet fekete pixel. Ha a keresésünk eredményes volt (a kezdőponttól 5 irányban fekete pixelt találtunk) úgy ennek attribútum értékét eggyel megnöveljük, koordinátáit (rendszerint lánckódját) beírjuk a listába, és az alap keresési irány S értékét kettővel csökkentve (S:=S-2), az eljárást előröl folytatjuk. Ha az S-1 irányban nem volt fekete pixel úgy következőnek az S irányban keresünk, és ha eredményesen, úgy a pixel kódját kiírjuk de S alapértékét nem változtatjuk meg és az eljárást előröl folytatjuk. Ha nem jártunk eredménnyel, úgy az S+1 irányban folytatjuk a keresést. Eredményesség esetén a pixel lánckódját kiírjuk, de S alapértékét most sem változtatjuk meg és az eljárást előröl folytatjuk. Ha mind ezideig nem találtunk új fekete pixelt, mely része a körvonalnak, úgy S értékét 2-el megnöveljük (S:=S+2) és ezzel a kiinduló értékkel az egész folyamatot megismételjük. Ha a folyamat háromszori ismétléssel sem vezet eredményre (a kezdő pixelen kívül több fekete kontúr pixelt nem talált a program), úgy a futást leállítjuk, mivel ez az eset akkor áll elő, ha egy magányos pixel kontúrját keressük. Ellenkező esetben, ha tehát a listán folyamatosan gyűlnek a körvonalat alkotó pixelek, a futás mindaddig folytatódik, míg az utolsó megtalált pixel nem lesz azonos (koordinátái alapján) a kezdő pixellel.
A keresés eredményeképpen rendelkezésünkre állnak a kontúrpontok koordinátáiból és iránykódjaiból álló listák. Természetesen elég csak a kezdőpont koordinátáit tárolni a többi koordináta szükség esetén ezekből az értékekből meghatározható. Az eredeti pixelkép attribútum értékei is módosultak mégpedig úgy, hogy azok a fekete pixelek, melyek a kontúr részeivé váltak a fekete pixeleket jellemző 1 helyett 2 vagy annál nagyobb attribútumokat kaptak. Mivel a keresés során minden határpontként figyelembe vett pixel attribútumát a program a kiválasztás pillanatában eggyel megnöveli, 2-nél nagyobb attribútum értékekkel úgy találkozhatunk hogy egyes pixelek többször is kiválasztásra kerültek a határ részeiként.
|
Ilyen
pixeleket úgynevezett többszörös pixeleket látunk a 2.29 ábrán. Az ábra tanúsága szerint a többszörös pixelek olyan vékony részletek határleírására szolgálnak amelyek mindkét oldali határát ugyanazon pixelek alkotják. A többszörös pixelek, mint arra később rámutatunk, fontos szerepet játszanak a vékony vonalak tengelyeinek meghatározásában. |
A tartomány valamennyi belső objektumának kontúrját a már vázolt külső kontúr meghatározó programra és annak eredményeire támaszkodva határozhatjuk meg.
Kiválasztunk a kezdőpontot követő fölülről lefelé haladó határszakaszon egy pixelt (megelőző iránykódjai 4-7, követő iránykódjai 5-7), ahonnan x (vízszintes) irányban pásztázni kezdjük a pixeleket. A vizsgálatba mindig három egymás után lévő pixelt vonunk be. A belső luk kezdőpontját, alapesetben, ott találja meg a program ahol a vizsgált három pixel közül az első két pixel értéke 0 és 1. Ekkor az 1 értékű pixelt tekintve kiindulópontnak, a határvonal kereső program megkeresi a belső luk határát ás hozzácsatolja a pixelek koordinátáit a külső kontúr listájához. Ez lehetővé teszi, hogy a belső határpontokról is indulhassanak pásztázások, melyek a még fel nem tárt belső lukakon belüli szigetek határait is feltárják.
Bonyolultabb az eset akkor, ha a luk határa és a teljes objektum határa egybeesik (a fehér lukat csak egy vékony fekete vonal választja el a külső fehér háttértől). Ekkor már mind a három egymás utáni vizsgált pixel attribútum értékét figyelembe kell venni a helyes döntéshez. A két határ egybeesése akkor áll elő, ha az egymás utáni bitek 0,2,0 értékeket vesznek fel. Abban az esetben ha a kérdéses bitkombináció 1,2,0 a pásztázás a globális objektum határához ért és új kezdőpontból kiindulva kell folytatni a keresést. Ugyanez a feladat akkor is ha a következő bitkombinációval találkozik a program: 0,3,0. Ekkor ugyanis az alapobjektum egy a fehér háttérbe kinyúló vékony "félszigetét" érte el a pásztázás, amely előtti és mögötti fehér részek már a háttérhez tartoznak.
Vékony objektumok tengelyvonalainak meghatározása (objektumvékonyítás)
A raszteres ábrázolás során erősen torzulnak az euklideszi geometria olyan hagyományos fogalmai mint a távolság, egyenes, metszéspont, hisz két tetszőleges pixel közötti i-út nem azonos az analóg síkon két pixelnek megfelelő pontok között húzható legrövidebb távolsággal, ha pedig két különböző pixel pár közötti i-utak metszéspontját vizsgáljuk az általában nem esik egy pixelre. Ezek a problémák világossá teszik, hogy ilyen jellegű feladatokat célszerűbb az analóg teret geometriailag leképező vektor modellben végrehajtani. A vektor modellt viszont csak akkor tudjuk létrehozni, ha meghatározzuk, hogy mikor tekinthetünk egy pixel formációt vonalszerűnek. Az egyik meghatározás szerint raszteres vonalábrázolásnak olyan pixel halmaz tekinthető, melynek valamennyi pixele egyben a halmaz körvonalának is része.
A raszter képek létrehozásakor az analóg képen vonalként jelentkező objektumok azonban nem feltétlenül felelnek meg a fenti meghatározásnak azaz a pixeles képen az eredeti vonalak teli objektumként is jelentkezhetnek az eredeti vonal vastagság illetve a pixelméret függvényében. Ahhoz, hogy az eltorzult vonalak vonalszerűségét a pixeltérben is helyreállíthassuk célszerű volt bevezetnünk a többszörös pixelek fogalmát.
A 2.30 ábrán szemléltetjük azokat a feltételeket, melyek közül egy vagy több fennállása esetén a pixelt többszörösnek nevezzük.
|
Többszörös a pixel ha:
|
A többszörös pixelek a határvonal meghatározó algoritmus többszörös futtatásával szekvenciális futási módban egyszerűen meghatározhatók: az első futás után az első feltételnek megfelelő pixelek értéke 2-nél nagyobb, a második futtatás során kiválaszthatók a második és harmadik feltételt kielégítő pixelek (nincs 1 értékű szomszédja illetve 2 vagy nagyobb értékű d-szomszéd megléte, mely ugyanakkor nem szomszéd a határt leíró útban). Az irodalomban [7] több olyan párhuzamos feldolgozást biztosító kritérium rendszert is találunk, ahol annak eldöntése, hogy valamely pixel többszörös-e vagy sem a szomszédos 8 pixel által alkotott konfiguráció vizsgálatára korlátozódik.
A vékonyítási algoritmusok alapgondolata az, hogy a síkbeli objektumokat vázukkal (más szóval középtengelyükkel) helyettesítjük, és hogy ez a váz a pixeltérben lehetőleg egy pixel vastag legyen.
|
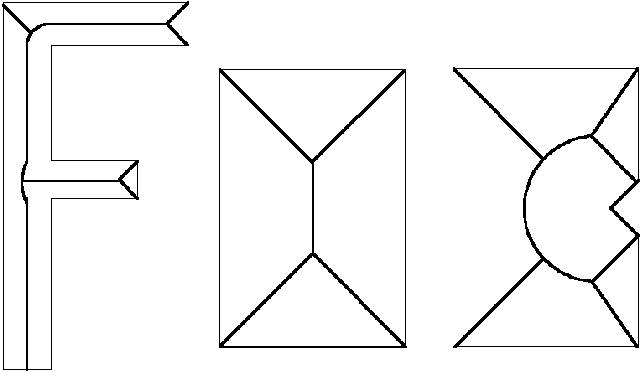
A folytonos síkon a vázat azon körök középpontjainak egymásutánja határozza meg, melyek teljes egészében benne vannak az objektumban, s melyeknél nagyobb, azonos középpontú köröket az objektum nem tartalmaz. Amennyiben az objektum határán lévő görbületi középpontban a görbület szélső értéket vesz fel úgy a váznak létezik egy olyan ága, mely a kérdéses pontban végződik. A 2.31 ábra tanúlsága szerint vékony objektumok esetén (az ábra F betűje) a váz jól tükrözi az objektumok alakját, ugyanez a vastag objektumokról nem mondható el. Ebből következik, hogy míg a vékony objektumok vektoros leírására vázukból indulunk ki, addig a vastag objektumok vektoros leírásához körvonalaikat használjuk fel. |
|
A vékonyító algoritmus szempontjából a tengelypontokat azonosnak vehetjük a többszörös pixelekkel, mivel ezek tulajdonképpen azok a pixelek, melyek a vonalas objektum két határát egy, legfeljebb két pixelen képezik le.
Az alap algoritmus szavakban a következőképpen fogalmazható
meg. Legyen R
az objektumot alkotó pixelek halmaza, B(R) a halmaz határa, M(R)
az R halmaz többszörös pixeleinek részhalmaza. Határozzuk meg a B(R)
halmazt olymódon, hogy minden olyan pixelt tartalmazzon, melynek d-szomszédja
van R-en kívül (azaz 0 értékű d-szomszédja van). Határozzuk meg
ezután M(R)-t, valamennyi határ pixelt mint lehetséges jelöltet
figyelembe véve, a párhuzamos feldolgozást lehetővé tevő 8 szomszédból álló
konfiguráció vizsgálata alapján.
Ha B(R) megegyezik M(R)-el, azaz valamennyi határpixel egyben többszörös pixel is, az alapfeladatot megoldottuk és a program leáll, ha nem R-et R-(B(R)-M(R))-el helyettesítve megismételjük az eljárást (azaz elhagyjuk azokat a határpont pixeleket, melyek nem többszörös pixelek és az így nyert redukált halmazon megismételjük a műveleteket). Az ismétléseket addig folytatjuk, míg a határ valamennyi pixele nem többszörös pixel.
Az így nyert alakzat általában 1, de helyenként 2 pixel vastagságú is lehet, ezért egy következő szerkesztési lépésben gondoskodni kell arról, hogy a váz két pixel vastag szakaszain az egyik (pld a 4 vagy 2 irányú, más szóval nyugati vagy északi) pixelt töröljük, ha ez nem megy a folytonosság rovására.
A bináris váz vektorizálása, az íveket alkotó pontok ritkítása
Az így nyert váz még nem vektor, hanem egy vékony vonalszerű bináris kép. Ahhoz hogy a vektorizálás megtörténjen még két lépés hátra van. Az első lépésben létre kell hoznunk a vékony bináris kép topológiáját. A topológia létrehozásánál abból indulunk ki, hogy a vektoros modellben azokat a pontokat nevezzük csomópontoknak, melyekben kettőtől eltérő számú vonal találkozik. Feladatunk most már az, hogy analógiát találva a vonaltalálkozásra a vékony bináris képen megkeressük a csomópontok pixeles megfelelőit és a közöttük elhelyezkedő íveket leképező pixeleket.
Az analógia megtalálására az ad egyszerű lehetőséget, hogy a bináris képünk egy pixel vastagságú, ami azzal egyenértékű, hogy azok a pixelek lesznek a csomópontok megfelelői, melyeknek kettőnél több vagy kevesebb szomszédjuk van .
|
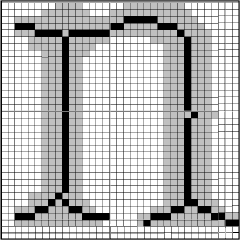
A 2.32 ábrán bemutatjuk egy "n" betü szkennelést követő vékonyítását (vázkialakítását), valamint a topológia létrehozását a vázon. A szkennelt pixeleket szürke, a váz pixeleket fekete kitöltéssel jelöltük (felső ábrarész), a három felé elágazó csomópontokat a kezdőpontokat jelölő (egy elágazással rendelkező) csomópontoktól az eltérő szürkeség árnyalat különbözteti meg (alsó ábrarész). A közbenső (kétfelé elágazó) pontok fekete kitöltést kaptak. |
Eljárásunk tehát az lehet, hogy valamilyen gráf bejáró algoritmussal elkezdjük bejárni a pixeleket. Tetszőleges helyen (pld. a bal felső pixelnél) kezdhetjük meg a vizsgálatot. Megnézzük, hogy hány szomszédja van, ha csak kettő úgy tároljuk egy pufferban a koordinátáit, a veremben az egyik szomszédja koordinátáit és hozzákezdünk a másik szomszéd vizsgálatához. A folyamatot mindaddig folytatjuk amíg olyan pixelhez nem jutunk, melynek kettőtől eltérő számú szomszédja van. Ha a szomszédok száma 1, úgy egy végcsomóponthoz jutottunk. A pufferben lévő koordinátákhoz hozzáfűzve a külön is tárolt végcsomópont koordinátáit egy rész ívet nyerünk.
Ezután előhívjuk a veremből a kezdő pont még nem vizsgált szomszédjának a címét és a vizsgálatot onnan folytatjuk (vázolt eljárásunknál gondoskodni kell arról, hogy a következő pontok koordinátái a pufferban az első vizsgált pont elé kerüljenek, ha ezt a problémát meg akarjuk kerülni, úgy kezdőpontként csomópontot kell választani).
Amint elérünk a következő kettőtől eltérő számú szomszéddal rendelkező csomóponthoz koordinátáit hozzákapcsoljuk a pufferből kivett koordináta sorozathoz és ezzel megkaptuk az első ívet a kezdő és vég csomóponttal. Ezen a csomóponton verembe helyezzük az egyik kutatható irányt a másik irányban pedig folytatjuk a bejárást az előbbiek szerint.
A bejárás eredményeképpen megkapjuk a vonalak kezdő, közbenső és végponti koordinátáit. Ez a struktúra elvileg már vektor struktúra gyakorlatilag azonban még szükség van az íveket alkotó pontok fogyasztására.
Bár az elmondott elvek alapján megszerkesztett programok már jó egy évtizede működnek figyelemre méltó, hogy a legújabb térinformatikai szakirodalom is egyre újabb és újabb programokról és program módosításokról számol be. Ez a tény több okkal magyarázható, közülük csak a négy legfontosabbra utalunk:
- a kezdeti algoritmusokat elsősorban nyomdatechnikai (betűszedési) célokból dolgozták ki;
- a topográfiai térképek tömeges szkennelése csak néhány éves múltra tekint vissza;
- a nagyméretarányú térképek tömeges szkennelése napjainkra vált reális igénnyé;
- a szkennelési eredmények feldolgozására egyre inkább szekvenciális működésű számítógépeket használnak.
|
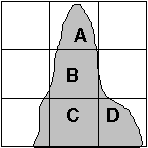
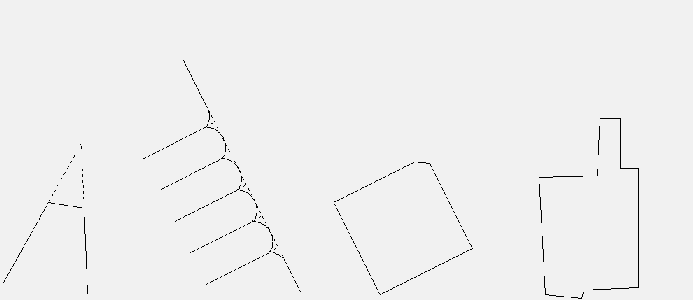
A 2.33-es ábrán azokat a tipikusan a nagyméretarányú térképek szkannolásánál fellépő hibákat mutatjuk be Aalders nyomán [8], melyek a nem kompatibilis felbontóképességből (nem megfelelő pixelméretből) adódnak. |
A 2.34 ábra esetében például az 1, 2 és 3 számmal jelölt pixelek megtartása lehetővé teszi az Y illetve T torzulás kiküszöbölését. |
A 2.34 ábrán a vékonyító algoritmus önkényes tájékozás választásának (az egy pixeles szélességet eredményező törlésnél) hatására létrejövő Y és T jellegű torzulásokat ábrázoltuk Drumond és szerzőtársai előadása alapján [9]. A hivatkozott szerzők előadásaikban arról számolnak be, hogy milyen algoritmusokat dolgoztak ki illetve szándékoznak kidolgozni a bemutatott hibák kiküszöbölésére. |
A fentiekből mindenesetre azt a következtetést mi is levonhatjuk, hogy a szkennelés eredményeinek vektorizálását csak akkor lehet többé kevésbé egyértelműen megvalósítani, ha szabványosítjuk az egyes térkép típusokhoz rendelhetően a szkennelési technikát (pixelméret), és a vékonyító és vektorizáló algoritmusokat (természetesen ugyanez vonatkozik a vektorizált pontok ritkitására is, amire a későbbiekben még kitérünk).
Mivel a szekvenciális számítógépek alkalmazásának a egyre nagyobb szerepe van a raszter-vektor átalakítás térinformatikai felhasználásában az alábbiakban röviden összefoglaljuk Moore 1992-es vektorizáló algoritmusát [10]. Megjegyezzük, hogy az algoritmus lényegében csak annyiban tér el a már felvázolt gráf követő algoritmustól, hogy szisztematikusan intézkedik az egész kép bejárásáról (a korábbi algoritmus csak egy objektum megtalálásáig keresett szisztematikusan), valamint hogy a végleges topológiát két lépcsőben alakítja ki.
|
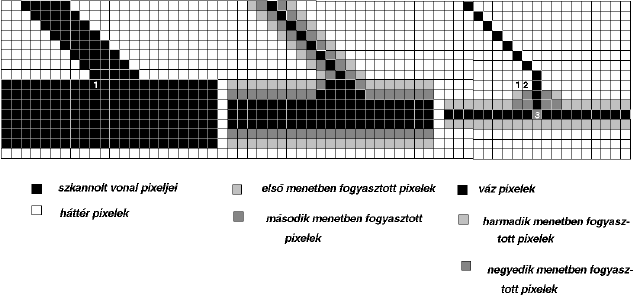
A módszer első lépcsőben soronként megvizsgálja a pixeleket és ha a pixel értéke 1 (fekete), úgy a 8 szomszédja milyenségét figyelembe véve kialakít egy kódot (2.35 ábra) mégpedig olymódon, hogy azoknak a szomszédoknak a kódját összeadja, melyek feketék tehát valamely vonaldarabhoz tartoznak. A kód kialakítása után egy szabálygyűjtemény megmondja, hogy az adott kódhoz a 16 szabály közül melyik tartozik. Figyelembe kell ezenkívül még venni, hogy a négy előzőleg feldolgozott pixel milyen vonalhoz tartozik. A szabályok megmondják hol kell csomópontot csinálni, melyik vonalat kell lezárni, meghosszabbítani stb. A végrehajtott szabályok illetve az "elődök" hovatartozása alapján csomópont-vonal, vonal-csomópont listák készülnek a másodlagos vektorizálás támogatására. A másodlagos vektorizálásra azért van szükség, mert a szabályok alapján "álcsomópontok" is kialakulnak (olyan pontok, melyeknek csak két elágazásuk van, tehát közönséges közbenső pontnak tekintendők). Maga a folyamat tulajdonképpen egy gráf bejárás, a program végig megy minden vonalon és megvizsgálja, hogy egy csomópont hány vonalban található meg. Ha a csomópont két vonalban jelentkezik, úgy törli a csomópontot és a két vonalat összekapcsolja. |
A vektorizált pixelpontok azonban igen sűrűn vannak, különösen, ha az eredetijükül szolgáló analóg vonalak egyenesek vagy szabályos ívek voltak. A ritkításra szabálytalan görbék (pld. szintvonalak) esetében is szükség van, azonban grafikus végtermék esetén, a sokszög vonalakat valamilyen approximációs eljárással, rendszerint spline-okkal, még simítani szokták.
A közbenső pontok ritkításánál három szempontot kell figyelembe vennünk: a kihagyandó pontok eltérése a helyettesítő egyenesüktől nem haladhat meg egy megadott értéket, az eltérések előjele váltakozó kell hogy legyen, az eredeti pontsor hossza a helyettesítő egyenes hosszánál nem lehet sokkal nagyobb (gyakorlati tapasztalatok alapján, ha ez a viszony 1,1 vagy kisebb a helyettesítés minden egyéb vizsgálat nélkül elvégezhető, ha a viszony 1,5 vagy nagyobb a helyettesítést el kell utasítani).
A poligon illesztő algoritmusok kis csoportokra bontják az illesztendő pontokat (számuk csoportonként rendszerint 5-10) majd megvizsgálják az előző bekezdés kritériumait (ha a vizsgált pont koordinátái xP, yP a vonalszakasz kezdőpontjának koordinátái X,Y a vonalszakasz tengellyel bezárt szöge µ, úgy az eltérés m=(yP-Y)cosµ-(xP-X)sinµ ). Amennyiben a szakasz megfelelt a kolinearitási feltételeknek úgy megkezdik a következő szakasz vizsgálatát, ha nem, úgy csökkentett pontszámmal megismétlik a vizsgálatot. Ha már két egymás utáni egyenes szakasz megfelelt a feltételeknek a program összehasonlítja irányszögeiket s amennyiben eltérésük egy megadott küszöböt nem halad meg a két egyenes szakaszt egybeolvasztja, azaz megszünteti az eredetileg az első szakasz végére tervezett töréspontot. A folyamat csomóponttól csomópontig tart, az eredmény pedig az ív megmaradt pontjainak koordináta jegyzéke.
A vektor-raszter konverzió
Bár a pillanatnyi gyakorlat elsőbbséget biztosít a raszter-vektor konverziónak a tudományos irodalomban mind több olyan tanulmánnyal találkozunk, mely a hibrid rendszerek nagymértékű elterjedését prognosztizálja a közeljövőben.
Ezek a rendszerek képesek mind a raszteres mind a vektoros adatok fogadására s a különböző műveleteket mindig abban a formában végzik amely a végrehajtás szempontjából előnyösebb. Az ilyen működési elv azonban feltételezi a rendszeres kétirányú konverziót, ami megnövelte az érdeklődést az egyszerűbbnek tűnő vektor-raszter átalakítás iránt is.
A téma első megjelenése annak köszönhető, hogy a számítástechnikában a korai vektoros grafikus képernyők helyét elfoglalták a raszteres grafikus eszközök. Az egyik megoldandó probléma tulajdonképpen az volt, hogy a különböző matematikai görbéket milyen sűrű paraméter értékekkel kell kiszámolni ahhoz, hogy a képernyőn a görbét reprezentáló pixelek, függetlenül a görbe szakaszától, egyenlő távolságokra jelenjenek meg, s ennek következtében a görbe rajzának egyenletes vonalvastagsága és tömöttsége legyen az egész ábrázolási tartományban. A másik probléma, a kerekítési hibákból adódó fogazottság, különösen a kis felbontású monitorokon rontotta az ábrázolás minőségét.
A térinformatika szempontjából a vektor-raszter átalakítás megoldandó kérdései kissé más aspektusból jelentkeznek. Bár igaz az, hogy mind munka közben, mind az eredmény elkészülte után grafikus eszközöket is alkalmazunk (képernyő, mátrixplotter) ezek vezérlése rendszerint a gyártók által szállított meghajtókkal történik és nem hat vissza a térinformatikai rendszer állományára. A rendszer állományában tárolt vektoros adatok rendszerint nyílt vagy zárt sokszögek, melyeket legfeljebb a megjelenítés szakaszában a rajzi fájlban simítanak valamilyen görbével. Számunkra tehát az a lényeges, hogy az egyenes darabok egyértelműen és lehetőleg visszaállíthatóan nyerjék el raszteres alakjukat.
Másik, speciálisan a térinformatikai rendszerek belső működését érintő probléma a raszteres alrendszer felbontása. Bizonyos globális vizsgálatokra a durva felbontás indokolt lehet, ugyanakkor nem akadályozhatja, hogy finomabb vektoros struktúrák bedigitalizálása esetén azok raszterizált formái a struktúrában megjelenhessenek (nem árt rámutatni, hogy hasonló problémákkal találkozunk a hagyományos topográfiai térképeken is, ezek megoldására találták ki a méreten felüli és az eltolt ábrázolást).
Térjünk vissza a vonaldarab raszterizálására. Állapodjunk meg mindenek előtt abban, hogy a koordináta rendszer kezdőpontja a raszter mező bal alsó sarokpontja. Ez a megállapodás nem fölösleges, mivel gyakran a bal alsó pixel közepén veszik fel az origót. Ezután az egyenes egyenlete alapján a független változó egész értékeire kiszámítjuk a függvény értékeket. Az iránytangens egynél nagyobb értékeire a függő és független változó értékeit felcseréljük.
A megkapott függvény értékek kerekítésénél úgy járunk el, hogy ha a vonal két szomszédos cellát is érint csak azt feketítjük be amelyiken a hosszabb utat teszi meg (ehhez meg kell vizsgálni a két egymás után következő y értéket és amennyiben a cellahatár kerek értékétől ellenkező értelemben térnek el, úgy az a cella változik feketévé, mely irányában a nagyobb eltérés jelentkezik). |
|
A raszteres rendszerek előnyei a területekkel végzett műveletekben fejeződnek ki a leginkább, ezért indokolt röviden kitérnünk a vektor poligonok raszteres átalakítására. Az átalakítás alapelve a topológiai modellel kapcsolatban már ismertetett paritás vizsgálat azaz a zárt idomoknak az a tulajdonsága hogy a belső pontjaikból húzott félegyenesek az idom határvonalával páratlan számú pontban metsződnek.
|
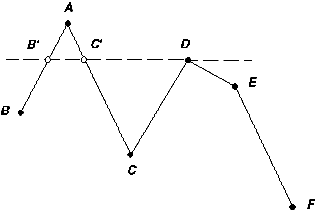
A számítástechnikai megvalósítás során a határoló egyenes darabokat maximális y és minimális x koordinátájú sarokpontjaikkal, valamint a másik végpontjukat meghatározó, Dx és Dy koordináta növekményeikkel írjuk le. Ezután rendezzük az oldalakat olymódon, hogy egymásutánjukat y értékük nagysága, iletve azonos y esetén, Dx-ük kicsisége határozza meg. A 2.37 ábrán az oldalak, ezek szerint, a következő sorrendben következnek: AB, AC, DC, DE, EF,... . |
|
A raszter átalakítás fentről lefelé irányuló soronkénti letapogatással történik. Tekintettel az y nagysága szerinti rendezettségre a letapogatást elég ymax csonkolt értékénél megkezdeni. A program meghatározza a vízszintes sor metszéspontjait a sorba állított aktív egyenes szakaszokkal. A kapott metszéspontoknak megfelelő oszlopkoordináták meghatározásához figyelembe kell venni a következő sorral alkotott metszéspontot is a célból, hogy a határvonalon csak olyan pixelt feketítsünk be melynek a vonal több mint ötven százalékát magába foglalja.
Az egy sorhoz tartozó raszterizált metszéspont koordinátákat listába foglaljuk és megnézzük, hogy a vizsgált pixeltől balra (kisebb x vagy oszlop koordinátával) hány metszéspont található. Ha ezek száma páratlan, úgy a pixelt befeketítjük, ha páros nem. Az eljárást mindaddig folytatjuk, míg a sor utolsó metszéspontjához nem érünk.
Ezután áttérünk a következő sor letapogatására. Az új sor y koordinátáját összehasonlítjuk a már vizsgált oldalak legkisebb y koordinátáival illetve a sorban következő oldal(ak) legnagyobb y koordinátá(i)val és az összehasonlítás eredményeképpen változatlanul hagyjuk illetve módosítjuk a metszéspontszámításnál figyelembe veendő oldalak listáját.
A vizsgálatot utoljára azzal a sorral futtatjuk le melynek y koordinátája megegyezik a legalsó sarokpont csonkolt y értékével.
· a következő részben a síkbeli transzformációkkal megkezdjük a kétdimenziós vektoros adatokkal végzett műveletek tárgyalását,
· visszatérhet az előző részhez is,
· vagy a tartalomjegyzékhez.
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc