GIS műveletek III

Ebben a részben folytatjuk a GIS elemző műveletek tárgyalását. Először a legfontosabb GIS művelettel

a fedvényezés (overlay) művelettel foglalkozunk, majd bevezetjük
a védőövezetek vagy buffer zónák fogalmát.

Fedvényezési (overlay) eljárások

A fedvények egymásra illesztését a regionális tervezési gyakorlat még a digitális módszerek bevezetése előtt a 60-as évek végén vezette be. Gyakorlatilag a dolgot úgy oldották meg, hogy a különböző tematikus térképeket átlátszó transzparensre rajzolták és a különböző tényezők együttes hatását átvilágító asztal felett regisztrálták. Nem nehéz elképzelni, hogy mennyire munkaigényes volt ez a feladat, s hogy mennyire szerények voltak a módszer nyújtotta lehetőségek a korszerű számítógépes módszerekhez hasonlítva.

Ha meg akarjuk fogalmazni a fedvényezési eljárás mibenlétét, úgy azt mondhatjuk, hogy alapértelmezésben ez az eljárás összekapcsolja az ugyanazon a földi ponthoz tartozó, az eljárásba vont különböző fedvényeken szereplő attribútumokat. Ha az attribútumok a különböző rétegeken azonos tulajdonságra vonatkoznak és azonos dimenziójúak, illetve egymással értelmesen műveletbe hozhatók úgy az összekapcsoláson kívül a fedvényezés keretében különböző aritmetikai és logikai műveleteket is el lehet rajtuk végezni. Ezekre a műveletekre azonban legtöbbször a levezetett értékek vonatkozásában kerülhet sor.

Azonos tulajdonság jellemző esetén az összeadásnak vagy kivonásnak akkor van csak értelme, ha a két fedvény különböző időpontban rögzítette az adott tulajdonságjellemzőt és a fedvényezésből a változásokra kívánunk következtetni. Például két ugyanarra területre vonatkozó különböző időben készült népsűrűségi térkép különbségéből megkapjuk a népsűrűség változási térképet egy adott időszakra.

Egymásra ható tulajdonság értékek műveletbe hozását rendszerint a földrajzi modellezésben alkalmazzuk. Ilyen feladat lehet például valamely vízgyűjtő terület elemi lefolyási tényezőinek meghatározása. Tételezzük fel, hogy az elemi lefolyási tényező () függ a vegetációtól, a lejtő kategóriától és a talaj porozitásától . A szemléletesség kedvért, mivel a legprimitivebb raszteres GIS lehetőségeit is be szeretnénk mutatni, alkalmazzuk az alábbi leegyszerűsített lineáris modellt:

ahol a k_i-k tapasztalati állandók, az átlagos lejtőszög fokban, p a porozitási osztály, v pedig a vegetációs osztály azonosítója (sorszám jellegű kódja).

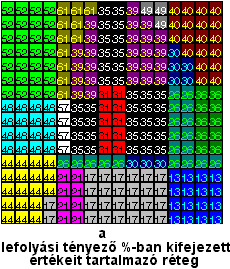
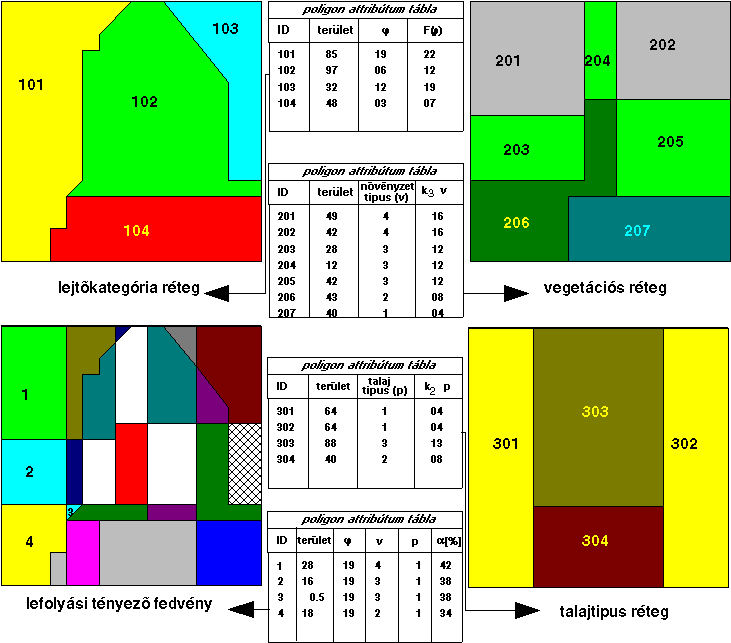
A 4.18 ábrán tüntessük fel a szintén leegyszerűsített lejtőkategória, talajtipus és növényzet tipus rétegeket. Ez utóbbi leegyszerűsítésre azért volt szükségünk, mivel ugyanazt a feladatot be szeretnénk mutatni mind raszteres mind vektoros kódolásban. Ez viszont azzal a következménnyel jár, hogy minden pixelbe be kell írnunk tulajdonság jellemzőjét ez pedig egyszerű rajztechnikai okokból azt vonja maga után, hogy a raszterünk nagyon durva lesz, illetve a vektoros rétegek objektumait túl szabályos vonalak határolják.

Legyen k₁=1.70, k₂=4.20, k₃=4.10, az alábbi osztályozási kódok figyelembevételével:

p	talajtípus	v	növényzet típus
1	igen áteresztő talaj	1	zárt erdő, laza hordalék
2	áteresztő talaj	2	feltört kultúrtalaj, erdő
3	közepesen áteresztő talaj	3	rét, legelő
4	igen vízzáró talaj	4	kopár szikla

4.18 ábra - egyszerűsített rétegek a lefolyási tényező modellezéséhez

A 4.19 ábrán feltüntettük az elemzés részeredményeit és végeredményét. Első lépésben átkódoltuk a lejtőkategória, talajtípus és növényzet típust ábrázoló rétegeket olymódon, hogy a megfelelő rétegen az egyes raszterpontok 'értékeit' sorra megszoroztuk k₁-el, k₂-vel és k₃-al. A második lépésben összeadtuk az átkódolt fedvények megfelelő pixeleinek 'értékeit' és az így nyert fedvény szolgáltatta a végeredményt.

4.19 ábra - a lefolyási tényező meghatározása

Ha általánosítani akarjuk a példa kapcsán megszerzett tapasztalatokat, úgy azt mondhatjuk, hogy még a legegyszerűbb raszteres rendszerek is alkalmasak az aritmetikai fedvényezésre, mely művelet során két vagy több fedvény megfelelő pixelértékein aritmetikai müveletet (összeadás, kivonás, szorzás, osztás) hajtunk végre, a művelet eredménye egyenlő az eredő fedvény megfelelő pixelének értékével. Ha a rendszer csak az alapműveletek végrehajtására alkalmas, úgy az aritmetikai fedvényezést rendszerint átkódolás előzi meg. Az átkódolás során a fedvények pixel értékeit globálisan vagy lokálisan megváltoztatjuk.

Lássunk egy teljesen más jellegű példát. Kényelmi okokból maradjunk a 4.18 ábra három fedvényénél, és próbáljunk meg a segítségükkel olyan területet találni, mely alkalmas lehet egy sportpálya céljaira. A feladatot továbbra is a legegyszerűbb raszteres rendszerrel kívánjuk megoldani.

Tételezzük fel hogy azt a területet tartjuk alkalmasnak a sportpálya céljaira, mely lejtőszöge nem nagyobb 6 foknál, talajtípusa igen áteresztő vagy áteresztő (1 vagy 2), növényzet típusa pedig rét vagy szántó (3 vagy 2).

Első lépésben, a 4.20 ábra szerint átkódoljuk a fedvényeket olymódon, hogy az alkalmas pixelek értékét 1-el tesszük egyenlővé, az alkalmatlanokét 0-val (az ábrán a zérusok kiírásától eltekintettünk).

4.20 ábra - sportpálya elhelyezési terve

Második lépésben kikeressük azokat a pixeleket, melyek valamennyi érintett átkódolt bemenő fedvényen 1-es értékkel rendelkeztek. Ezek a pixelek az eredmény fedvényen is 1-es értéket kapnak, míg a többi pixel értéke 0 lesz.

Az elvégzett műveletet logikai szorzásnak nevezik műveleti jele , illetve a programnyelvekben AND. Ha tehát az eredmény fedvény i,j-ik pixelét c_ij-vel a bemenő fedvények megfelelő pixeleit pedig sorra l_ij-vel, v_ij-vel és t_ij-vel jelöljük, úgy az elvégzett művelet a következő alakban írható fel

c_ij=l_ijv_ijt_ij,

mely értéke 1, ha a jobboldalon található valamennyi tényező értéke 1, illetve 0, ha a jobboldali tényezők közül egy vagy több értéke 0.

Mivel a művelet a fedvények valamennyi pixelén végrehajtandó, az egyszerűség kedvéért, indexek nélkül fedvényekre felírva szokott szerepelni a GIS utasításokban, azaz pld. alkalmas=mvegetacio AND mlejtokategoria AND mtalajtipus. Amint a példából is látszik a tényezők sorrendje felcserélhető.
Megjegyezzük, hogy más logikai műveletek is használhatók a fedvények között. A logikai szorzás után leggyakrabban a logikai összeadást használjuk, melynek értéke 1, ha a tényezők közül legalább egy értéke 1 és 0, ha minden tényező zérus. A logikai összeadás műveleti jele , melyet a programozási nyelvek OR betűkombinációval helyettesítenek. Egyes programozási nyelvekben szerepel a XOR jelű két tényezős művelet is, mely értéke 0, ha a tényezők értéke azonos (mind a kettő 0 vagy mind a kettő 1), és 1 ha a tényezők különbözőek.

Mielőtt rátérünk a vizsgált feladat vektoros megoldására foglaljuk össze az egyszerű, részletes attribútum tábla nélküli raszteres rendszerek fedvényezésével kapcsolatban szerzett tapasztalatainkat.

Aritmetikai fedvényezéssel olyan fedvények között operálhatunk, melyek pixel értékei számtani műveletekbe vonva értelmezhető eredményt produkálnak. Ezzel a művelettel megoldhatjuk a földrajzi modellezés néhány leegyszerűsített feladatát.

2. A logikai fedvényezés a kiválasztást teszi lehetővé több, a műveletbe vont fedvények számától függő, kétértékű kritérium alapján.

3. A logikai fedvényezés minden esetben, az aritmetikai fedvényezés pedig igen gyakran igényli, hogy a bevont fedvényeket a műveletek megkezdése előtt átkódoljuk.

Vizsgáljuk meg ezután, hogy miként is történik a fedvényezés a vektoros rendszerekben.

Tételezzük fel, hogy a lejtőszög hatását a lefolyási tényezőre bonyolultabb, négyzetes kifejezéssel írjuk le, míg a talaj illetve a növényzet hatását továbbra a már ismert egyszerű alakkal vesszük figyelembe. E megfontolások figyelembe vételével a lefolyási tényezőre az alábbi képletet alkalmazzuk:

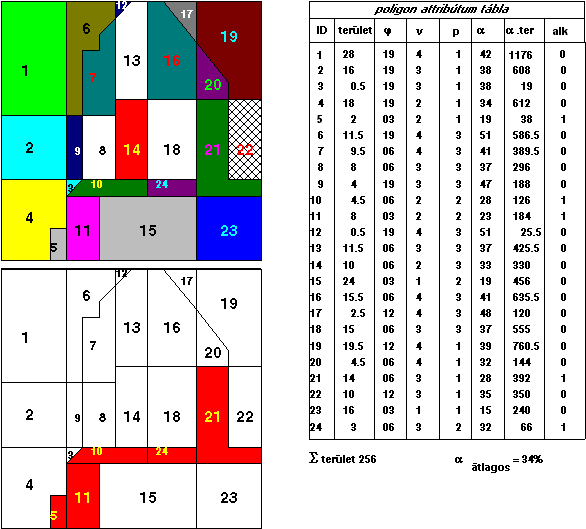
4.21 ábra - lefolyási tényező meghatározása vektoros GIS-ben

A 4.21 ábrán megkíséreltük fölvázolni a lefolyási tényező példa megoldását vektoros GIS esetében. Meg szeretnénk jegyezni, hogy az alkalmazott kifejezést nem tekinthetjük tudományos alapossággal levezetett formulának, kizárólag azért esett rá a választásunk, mivel jól szemlélteti a raszteres illetve vektoros GIS fedvényezési műveletek különbözőségét és hasonlóságát.

A legfontosabb különbség, mely az ábra kapcsán szemünkbe ötlik, hogy a vektoros GIS-ben ellentétben az egyszerű raszteres rendszerekkel minden fedvényhez tetszőleges részletességű attribútum táblázat tartozik, melynek minden sora egy-egy egyszerű objektumot jellemez. Ebben az attribútum táblázatban definiálhatunk olyan oszlopokat is, melyek értékét egy vagy több az adott táblázathoz tartozó oszlopon végrehajtott műveletek eredményeképpen nyerjük. Például a lejtőkategória fedvény utolsó oszlopát a kifejezésből számítja a rendszer (az, hogy milyen műveleteket használhatunk szoftverfüggő, nem minden rendszer teszi lehetővé például a trigonometriai függvények alkalmazását).

A fedvényezés eredményeképpen olyan objektumok jönnek létre, melyekre vonatkozóan a műveletben résztvevő fedvényeken lévő objektumoktól örökölt attribútumok állandóak. Azaz vektoros rendszerekben a fedvényezés eredményeképpen egyszerű objektumokból összetett objektumokat épít fel a rendszer. Az, hogy egy réteg mikor ábrázol összetett objektumokat és mikor egyszerű objektumokat tulajdonképpen relatív, ezért az oszlopok közötti műveletek az eredő rétegen is értelmezhetők (bizonyos rendszerek technikai okokból korlátozzák azokkal a levezetett rétegekkel végezhető műveleteket, melyeken különböző objektum típusok pld. vonalas és területi is szerepelnek).

A 4.21 ábrán helyhiány miatt nem töltöttük ki egészen az eredő réteg attribútum táblázatát, ezt a mulasztásunkat azonban a további műveleteket illusztráló 4.22-es ábrán pótolni fogjuk.

További feladataink közül először a vízgyűjtőre alkalmazható átlagos lefolyási tényezőt kell számolnunk. Nem nehéz rájönnünk, hogy ez nem más mint a szomszédsági műveletekkel kapcsolatban már ismertetett statisztikai programcsomagban a súlyozott átlag képzése: megszorozzuk valamennyi elemi lefolyási tényezőt az érintett terület elemmel, összegezzük a szorzatokat majd az összeget elosztjuk a vízgyűjtő terület összegével. Ha rendszerünk nem rendelkezik beépített statisztikai függvényekkel a kérdéses műveletet viszonylag egyszerűen magunk is megtervezhetjük illetve beprogramozhatjuk.

A következő lépésünk a sportpályának megfelelő területek kiválasztása lesz. Továbbra is a raszteres műveletekkel kapcsolatban már említett kritériumokkal dolgozunk, azaz feltételezzük, hogy az a terület jó sportpályának, mely lejtése , talajminősége 1 vagy 2, növényzet típusa 3 vagy 2.

A fedvényezés eredményeképpen létrejött kompozit (egyesített fedvény) attribútum tábláját kiegészítjük egy oszloppal, melyet pld. 'alkalmasságnak' nevezünk. Ezután felírhatjuk, hogy

if (AND (talajminőség = (1 OR 2)) AND (növényzet = (2 OR 3))) then alkalmasság = 1 else alkalmasság = 0 endif;

és a kifejezésből számíthatjuk az új oszlop értékeit.

4.22 ábra - kompozit fedvény és attribútum táblája vektoros GIS-ben

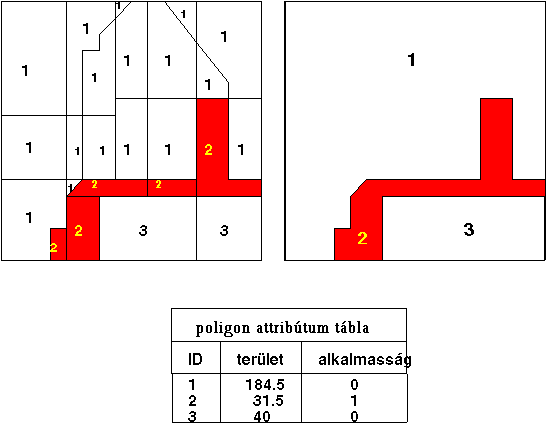
A következő lépésben megjeleníthetjük a kompozit fedvényt az új oszlop szerint színezve (pld. 1=piros, 0=fehér), ezután (két lépésben) az azonos színű szomszédos objektumokat egybeolvasztjuk majd eltöröljük a köztük lévő határokat (4.23 ábra).

4.23 ábra - sportpálya elhelyezési tervezés vektoros GIS-ben

Amint az ábrából feltűnik az új objektumoknak a területükön kívül csak egy attribútumuk van az alkalmasság. Ez az egyszerű objektum típusú koncepcionális modell alkalmazása esetén természetes, hisz az objektumnak ebben a modellben az a kritériuma, hogy önálló geometriai primitívet alkosson, valamint hogy az attribútumai konstansok legyenek. Mivel az egymásba olvasztott objektumoknak csak egy állandó attribútumuk van az alkalmasság, ezért az attribútum táblázatban ez fog szerepelni. Az ábra kapcsán az is egyértelmű, hogy a sportpályára alkalmatlan területeket azért kell két objektummá szervezni, mivel mind a két egység, a szelvény keretvonalait is figyelembe véve zárt sokszöget alkot.

A bemutatott helykiválasztási példa a fedvényezés alkalmazását kívánta csak illusztrálni, a valóságban az alkalmassági értékek rendszerint nem csak binárisak lehetnek, hanem egy megadott intervallumban, mondjuk 1 és 10 között változhatnak. Ha ennek a skálázásnak megfelelően alakítjuk ki az új objektumokat, úgy több objektumot kapunk és elképzelhető, hogy a végleges kiválasztásnál nem a legmagasabb alkalmassági osztályzattal rendelkező objektumot fogjuk sportpályának kiválasztani, mivel olyan tényezőket is figyelembe veszünk a helyszíni bejárás során melyek nem szerepelnek a GIS adatbázisban, vagy ha szerepelnek is alkalmazott számítási módszereink képtelenek a figyelembevételükre.

Vizsgáljuk meg ezek után a fedvényezés néhány technikai kérdését.

Először foglalkozzunk a raszteres rendszerekkel. Korábban már megismerkedtünk a quadtree struktúrában tárolt bináris raszteres képek halmazműveleteivel a metszettel és az unióval. Logikai fedvényezés esetén az elmondottak közvetlenül alkalmazhatók. Kissé módosulnak az eljárások, ha aritmetikai fedvényezést hajtunk végre. A módosulás lényege az, hogy az eredményfa azon csomópontjai, melyek valamelyik operandus levelével azonos helyen vannak tárolják a levél illetve a két fa közti művelet információit és átörökítik azokat az eredő levelekre.
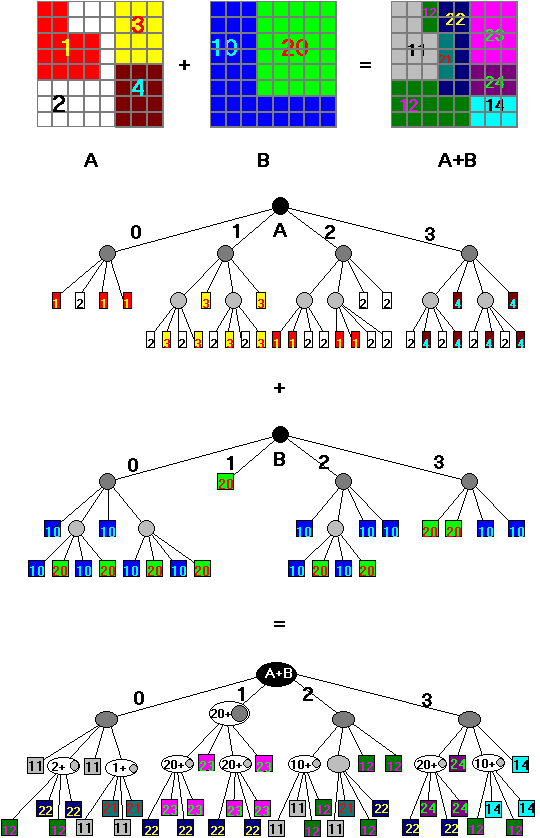
A módszer alapelvét egy egyszerű példával próbáljuk megvilágítani.

A 4.24 ábrán megrajzoltuk az A és B szelvényt, valamint összeadásuk eredményét azaz A+B-t.

Megrajzoltuk a megfelel quadtree-ket is. Az algoritmus úgy működik, hogy sorra veszi színtenként a csomópontokat, ahol mindkét gráfban csomópont van ott a megfelő csomópont az eredményben is egyszerű csomópont lesz, ahol az egyik gráfban csomópont van a másikban pedig levél ott az eredményben 'örökítő' csomópont keletkezik, mely tárolja a kérdéses levél tartalmát és a müveletet, ha a megfelelő csomópontok mindkét gráfon levelek, úgy az eredmény gráfban is levelet kapunk, mely értéke megegyezik a két levél közti művelet eredményével.

Az örökítő csomópont továbbadja tartalmát mind a négy leszármazottjának.
Példánk összeadást mutat be de ugyanezekkel a szabályokkal realizálhatjuk a többi aritmetikai műveletet is.

A quadtree negyedeit 0, 1, 2, 3 számokkal jelöljük valamennyi, zérustól eltérő hierarchia szinten (az ábrán helyhiány miatt csak az első hierarchia szintre mutató ágakat jelöltük). Az algoritmus megvizsgálja az egymásután következő hierarchia szinteken a megfelelő negyedeket és előállítja az eredmény quadtree megfelelő negyedét. Az A0 és B0 ágak mindkét fán szürke csomópontokra mutatnak, következésképpen az (A+B)0 csomópont is vegyes lesz, azaz csak a fiaira mutató pointereket fogja tárolni. Hasonló a helyzet az (A+B)2, (A+B)3 csomópontok esetében is. Az (A+B)1 csomópont azonban már értéket is kap, mivel B1 nem szürke csomópont, hanem levél, melynek értéke 20. A kérdéses értéket (A+B)1-ben tárolni kell, mivel szerepet fog játszani az összegfa következő szintjének létrehozásában.

A második hierarchia szinten A00=1 és B00=10, azaz mindkét megfelelő negyed levél, ezért az összegfa megfelelő negyede szintén levél lesz, mely értéke egyenlő lesz a két alkotó összegével: (A+B)00=11. Hasonló okokból (A+B)02=11. Más lesz a helyzet a 01 és 03 negyedekben, mivel A01=2 és A03=1 értékű levél, míg a megfelelő negyedek B-ben szürke csomópontok. Az elmondottak értelmében (A+B)01 és (A+B)03 örökítő csomópontok lesznek, melyek átadják fiaiknak a 2 illetve 1 értéket. Ha tehát például a 011 negyed értékét akarjuk meghatározni az összeg fán úgy B011=20 értékéhez az (A+B)01-ben örökített 2-t kell hozzáadni, hogy megkapjuk az összegfa megfelelő levelét: (A+B)011=22-t.

4.24 ábra - összeadás raszteres rendszerekben

A vektoros modellekben a fedvényezési művelet sokkal számításigényesebb, mivel nagyon sok vonalszakasz metszéspontot kell számítani, illetve fel kell építeni a metszések következtében létrejövő új objektumstruktúra topológiáját.

Bár a fedvényezés értelmezhető különböző objektumtípusokból összeállított fedvények között is, az esetek többségében mindkét műveletbe hozott fedvény poligon (terület) tipusu. Ez az eset egyben technikailag is a legbonyolultabb és a többi esetet (poligon tipusú pont tipusúval, vonal típusú poligon típusúval, vonal típusú vonal típusúval) úgy tekinthető mint ennek az általános esetnek egy-egy speciális, egyszerűsített változata.

A legtöbb egyszerűsítéssel a pont típusú fedvény és a poligon típusú fedvény egymásra fektetésénél élhetünk. Elvileg ezt a műveletet is konkatenálásnak (összekapcsolásnak) tekinthetjük, mivel a pontok attribútumához hozzákapcsoljuk annak a poligonnak az azonosítóját, amelyen belül található. Az elvi korlátozás abban van, hogy a közös fedvényben nem jön létre közös attribútum tábla (ennek ugyanis nem volna semmi értelme), hanem a pont attribútum tábla kiegészül a megfelelő poligon azonosítókkal, míg a poligon attribútum tábla a megfelelő pont azonosítókkal.
Ha például a pont típusú fedvény olajkutakat tartalmaz, a poligon típusú pedig a megyéket, úgy a kutak adatait tartalmazó táblázat sorai kiegészülnek annak a megyének a nevével, amelyben a kérdéses kút van, a megyék táblázatának sorai pedig a kutak azonosítóival (tekintettel arra hogy megyénként változó lehet a kutak száma, ez utóbbi táblázat kiegészítésre nem mindegyik rendszer alkalmas). Technikai oldalról a műveletet a pont a poligonban algoritmus pontonkinti futtatásával végzik a rendszerek.

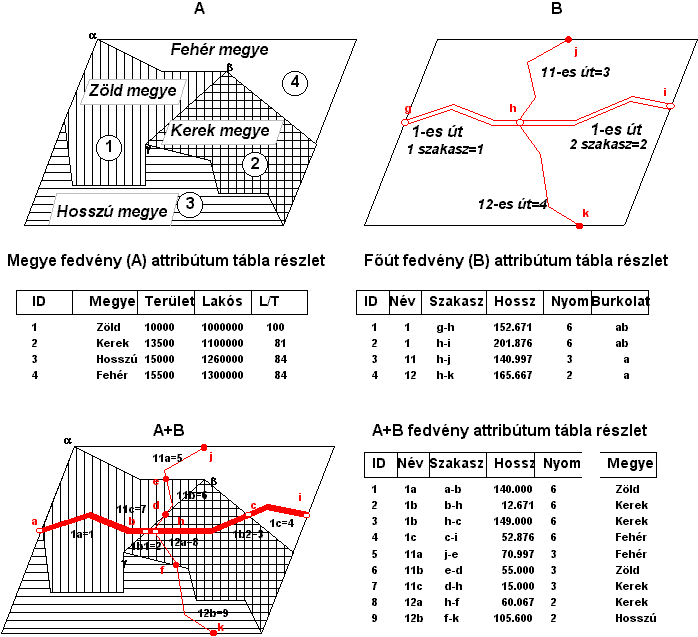
Vonalas tipusú és területi fedvények fedésbehozásakor a vonalas objektumok száma megnő. Példaként szolgáljon a 4.25 ábra, mely A fedvényén a megyehatárokat, B fedvényén pedig a főúthálózatot tüntettük fel. A két fedvény egymásra fektetése következtében megnő a vonalas objektumok száma, mivel az utak és megyehatárok metszéspontjai csomópontokat alkotnak, melyek részekre osztják az eredetileg homogén útszakaszokat. A fedvényezés eredményeképpen tehát módosulnak az objektumok illetve az attribútum táblázatok olyan értelemben, hogy megváltoznak az útszakaszok méretei és kiegészülnek annak a megyének a nevével, mely a kérdéses szakaszt tartalmazza.

Technikailag a poligon és a vonalas objektum metszéspontjait a korábban ismertetett módon számolják a rendszerek, az attribútum tábla kiegészítésére pedig a topológiai viszonyok logikai elemzése nyújt lehetőséget.

Vizsgáljuk meg például a 11-es út e-d csomópontok közötti szakaszát. A 11-es utat alkotó j-h ív az e pontban metszi a Zöld és Fehér megyét alkotó poligonok a-b ívét. Az A fedvény ív attribútum táblázatából (ezt az ábrán nem tüntettük fel) a program megállapítja, hogy a kérdéses ív baloldalán a 4-es, jobboldalán az 1-es objektum helyezkedik el. A következő metszéspontban a j-h ív a b-g ívet metszi, mely jobb oldalán az 1-es, baloldalán a 2-es objektum helyezkedik el. Mivel a két egymás utáni metszéspont A fedvényhez tartozó ívei az 1-es objektumban közösek, ez csak akkor lehetséges, ha a kérdéses szakaszt az 1-es objektum tartalmazza.

Ha a vizsgált szakasz végpontja már a B szelvényen is csomópont volt (például a h pont), úgy a pont a poligonban algoritmus meghatározza, hogy a kérdéses csomópont a fedvényezés után melyik poligonba kerül, a rá illeszkedő íveket értelem szerűen szintén ez a poligon tartalmazza, hisz az ív az eredő kompozit fedvényen csak addig tart, míg nem metsződik a poligon határvonalával. A fenti gondolatokat kiterjeszthetjük az eredetileg is a poligon határokon ábrázolt csomópontokra (a,j,i,k). Ha ezek a pontok szabatosan a poligon határán vannak, úgy az algoritmusok úgy kezelik őket mintha a poligonon belül lennének, ha pedig (ha kis mértékben is) kívül vannak a határon, úgy a rendszerek kiszámítják a tényleges metszéspontot s ezzel a megoldást visszavezetik az első esetre.

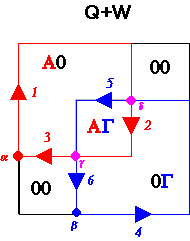
4.25 ábra - területi és vonalas fedvény egymásrafektetése

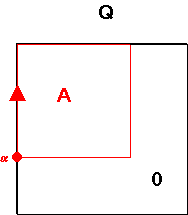
Térjünk rá ezután az általánosnak tekinthető poligon (terület) típusú objektumokat tartalmazó fedvények fedésbe hozására. A 4.26 ábrán két egyszerű poligont tartalmazó fedvényt tüntettünk fel. Feltételeztük, hogy az első poligon attribútumát A-al a másodikét G-val jelöljük, míg a háttér attribútuma mindkét fedvényen 0.

4.26 ábra - két területi fedvény egymásra fektetése

A fedvényezési művelet során a Q fedvényen lévő egy ívből álló poligon metszésbe kerül a W fedvény szintén egy ívből álló poligonjával, ami a és csomópontok létrehozását és koordinátáik kiszámítását eredményezi.

Az új csomópontok belépése következtében a kompozit szelvényen megváltozik az ívek száma és a zárt ívekből új poligonok azaz egyszerű objektumok jönnek létre. A továbbiakban az algoritmusok megkeresik az új ívektől jobbra illetve balra elhelyezkedő poligonok attribútumait és a közös attribútum illetve az összefüggő terület alapján létrehozzák az új objektumokat. Ez utóbbi lépés geometriailag az objektumokat határoló ívek sorozatainak összeállítását jelenti.

Nézzük meg a folyamatot a 4.26 ábra egyszerű példáján kissé részletesebben. Induljunk ki a Q fedvény álcsomópontjából. A csomópontból kiinduló 1 ív jobboldalán a Q fedvényen az attribútum érték A, bal oldalán 0; a csomópont koordinátáinak (0,1) megfelelő helyen a W szelvényen az objektum attribútuma 0. A fentiekből következik, hogy az eredő szelvényen az 1 ív jobboldali attribútuma A0, baloldali attribútuma pedig 00. A csomópontból (2,2) a 2 és 5 ívek ágaznak ki. A metszéspontot az A és attribútumú objektumokat alkotó ívek hozzék létre, ez tehát azt jelenti, hogy az 1 ív folytatásaként jelentkező 2 ív eredeti jobb illetve baloldali attribútumaihoz azaz A-hoz és 0-hoz hozzáadódik a metszett objektum attribútuma . A 2 ív jobboldali poligonjának attribútuma tehát A a baloldali poligonjáé pedig 0. A csomópontban (1,1) a Q fedvény objektumát alkotó ív elhagyja a W fedvény objektumát, azaz ugyanolyan poligonok fognak tőle jobbra és balra elhelyezkedni, mint az 1 ív esetében, név szerint A0 és 00. Folytassuk a vizsgálatot a álcsomópontból (1,0) kiinduló 4 ívvel. A Q szelvényen ez a koordináta a 0 attribútumú mezőbe esik, a W szelvényen pedig az ívtől jobbra 0, balra a poligon attribútuma. Következésképpen a 4 ív jobboldali poligonjának attribútuma 00, baloldali poligonjáé pedig 0. Mindez a pontig érvényes, mivel itt lép be a W objektumot alkotó ív a Q objektumba. Ez pedig azzal jár, hogy az eredeti jobb illetve baloldali objektum attribútumaihoz hozzáadódik A. Az 5 ív jobboldali objektumának attribútuma tehát A0, baloldali attribútumáé pedig A. A 6 ív jobb és baloldali objektumának attribútumai megegyeznek a 4 ív megfelelő értékeivel, azaz 00 és 0.
Ezután már a csatlakozó ívek alapján nem nehéz összeállítani az objektumokat határoló poligonokat: A0 - 1,5,3; A - 2,5; 0 - 4,2,6. A fennmaradó terület a 00 attribútumú háttér, melyre a továbbiakban nincs szükségünk.

A fedvényezés, amint azt a 'pogácsa szaggató' módszerrel kapcsolatban már említettük, több más GIS műveletben is szerepet kap, ilyen műveletek az említetten kívül az ablakolás és a védőövezet generálás.

Az ablakolás szinte minden korszerű rajzi szoftver szerves része, gyakran a nagyítással (zoomolás) együtt használják, de alkalmazzák objektumok kiválasztására is. Lényege, hogy a szoftver a pogácsa szaggatáshoz hasonlóan kivágja az objektumok azon részét, mely a felhasználó által a képernyőn kijelölt vagy billentyűzeten bevitt derékszögű négyszög (az ablak) belsejébe esik. Ebben az esetben tehát a műveletet logikai szorzásként definiálhatjuk, az első fedvényt (azt, amelyből ki akarjuk vágni az ablakot) a művelet objektumonként ideiglenesen 1 értékűre kódolja, míg a második fedvényen az 'ablak' belseje 1 értéket, míg a rajta kívül elhelyezkedő fedvény rész 0-t kap. A szorzás után csak az ablakon belüli részek maradnak meg a további műveletek céljaira.

Védőövezet (buffer zóna) generálás

Elemző, tervező feladatok megoldásakor a GIS talán leggyakrabban használt művelete a védőövezet vagy buffer zóna képzés. Bár ez a művelet is szoros kapcsolatban van a fedvényezéssel, tekintettel fontosságára külön pontban foglaljuk össze a vonatkozó legfontosabb ismereteket.

Szemantikailag a védőövezet generálás elsőrendű feladatát jól tükrözi magyar elnevezése: bizonyos objektumok köré, elsősorban az ivóvízellátás víztisztasági követelményeinek kielégítésére, olyan új objektumok létrehozásáról van szó, melyek pontjainak legrövidebb távolsága az eredeti objektumtól állandó.

Az eredeti vízvédelmi célok mellett sok egyéb feladat megoldására is alkalmazzák az övezet generálást, ezek legszámosabb csoportjával a szomszédságok (régiók) kijelölésével kapcsolatban már megismerkedtünk. Annak ellenére, hogy a hivatkozott pontban aláhúztuk az elvi különbséget a védőövezet és a szomszédság kijelölés között, a gyakorlatban sok szoftver egybe mossa magát a művelet-párt és a paraméterektől illetve a megelőző és követő műveletektől függ, hogy melyik osztályba sorolható a feladat.

Tulajdonképpeni védőövezettel találkozunk pld. a földalatti távvezetékek (gáz, olaj, víz, elektromosság, adatátvitel, stb.), föld feletti nagyfeszültségű vezetékek, vasutak, utak stb. környezetében. Ezek az övezetek gyakran fizikailag is jelölve vannak a földfelszínen és a létesítmény üzemeltetője szolgalmi jogot vagy kisajátítás útján tulajdonjogot szerez az övezetre. A védőövezet kijelölés célja ezekben az esetekben az, hogy a létesítmény illetve a környezet épsége valamint zavartalan funkcionálása érdekében megtilt bizonyos tevékenységeket ezen a területen. Ezekben az esetekben a védőövezet állandó objektum, mely része a digitális megvalósulási térképnek.

A szomszédsági vizsgálatoknál felhasználhatjuk például az övezeteket annak az előrejelzésére, hogy milyen hatással lesz egy út megépítése a környező természeti erőforrások biztonságára. Egyértelmű ugyanis, hogy ha az út közelében értékes erdőterületek találhatók, úgy az engedély nélküli fakitermelés növekedésével számolhatunk. Míg azonban az építési előírásokban rögzített védőövezetek esetén a konstans távolság megfelelő megoldást biztosít, addig a természeti jelenségek vizsgálatakor ez az egyszerűsítés nem mindig kielégítő.

Gondoljunk arra, hogy a felszíni vízfolyások vízvédelmi körzeteinek kijelölésekor a körzet természetes határa a vízgyűjtő terület, mely a domborzati viszonyok függvénye, és határai általában nincsenek állandó távolságra a vízfolyástól. Felszín alatti vizek esetén a helyzet még bonyolultabb, mivel a körzet határait a domborzaton kívül befolyásolják a felszín alatti rétegek helyzeti, szűrési és vízáteresztési paraméteri is.

Könnyű belátni azt is, hogy a példaként említett környezeti hatás vizsgálatnál, az értékes faállományt fenyegető veszély nem csak attól függ, hogy a kérdéses erdőterület milyen messze van az úttól hanem attól is, hogy milyenek a szállítási viszonyok az erdő és az út között, ezt pedig nagymértékben befolyásolják a domborzati, talajtani, vízelvezetési, stb. tényezők is.

A fenti meggondolások alapján megállapíthatjuk, hogy a földrajzi modellezésben a konstans távolságú védőzónák csak más tényezőkkel kombinálva több fedvény és művelet együttes felhasználásával nyújtanak kielégítő eredményt.

Technikailag a védőövezet generálását a 4.27 ábrán szemléltetjük. Amint az ábrából is látható a művelet inverze a raszter-vektor átalakításnál ismertetett váz kialakításnak.

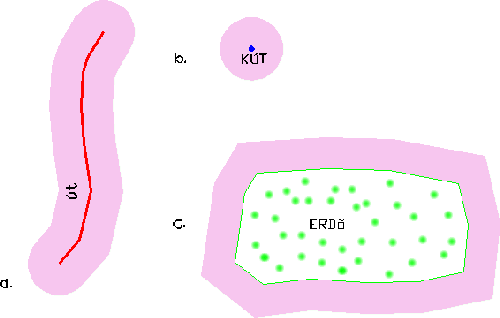
4.27 ábra - buffer zona generálás vektoros GIS-ben

Az a. ábrarész egy vonalas létesítmény (esetünkben út) védőövezetét mutatja be. A védőövezet geometriai meghatározása értelmében a védőövezet határpontjai azonos távolságra vannak a hozzájuk legközelebb fekvő objektumponttól. Ez a feltétel csak úgy teljesíthető, ha az övezet két végét félkörök alkotják. Pont szerű objektum esetén értelemszerűen kör alkotja a védőövezetet (b ábrarész), míg poligon esetén (c ábrarész) az objektumot alkotó poligon szögfelezőire illeszkednek a poligon oldalaival párhuzamos védőövezet oldalak.

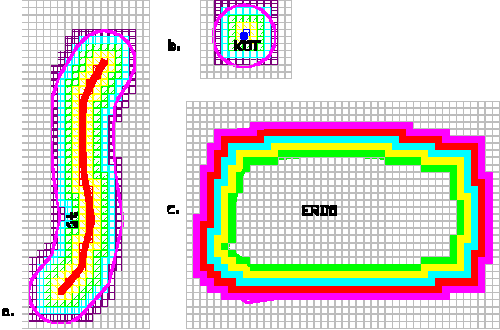
Nem nehéz elképzelni, hogy a fenti szerkesztések jelentős futásidőt igényelnek vektoros rendszerek esetén és a fedvényezéshez hasonlóan lassítják a feladatmegoldást PC-s környezetben. A fedvényezéshez való hasonlóság abban is kifejezésre jut, hogy raszteres rendszerekben a feladat a 4.28 ábra tanulsága szerint viszonylag egyszerűen oldható meg.

4.28 ábra - buffer zona generálás raszteres GIS-ben

Az a és b ábrák esetében a különböző övezet szakaszokat különböző sraffozási mintával ábrázolva próbáltuk szemléltetni az övezet képzést raszteres rendszerekben. Az eredeti vektoros ábrázolást itt nem takartuk el s így jól szemlélhető, hogy mennyire közelíti a raszter kép a vektoros vonalakat. A c ábra esetében az eredeti vonalakat letakartuk a kitöltött raszter cellákkal ezért csak néhány helyen látható a vektoros és raszteres ábrázolás eltérése. Talán nem szükséges említeni, hogy a raszteres ábrázolás szemmel látható torzítása annak a következménye, hogy a szemléletesség kedvéért durva felbontású, azaz nagyméretű raszter cellákat alkalmaztunk.