tulajdonképpen nem más, mint a 2l illetve 2k periódusú függvény helyettesítése

és

frekvenciájú
Ebben a részben tulajdonképpen folytatjuk a képfeldolgozással kapcsolatos ismereteink bővítéset és megismerkedünk néhány matematikai fogalommal, éspedig
Lehet, hogy az alcím kissé furcsának tűnik az olvasónak, ezért megpróbálom néhány szóban megmagyarázni. Képfeldolgozási kérdésekkel nem most találkozunk először. Viszonylag részletesen foglalkoztunk a bináris képekkel végrehajtható legfontosabb képfeldolgozási műveletekkel: a raszter-vektor, vektor-raszter átalakítással. A normálsztereogramm és ortofotó készítéssel kapcsolatban pedig azt is megnéztük, hogy hogyan lehet a tónusos képelemeket eltolva a képeket átalakítani (tulajdonképpen geometriailag torzítani), sőt e művelettel kapcsolatban a szürkeségi értékek interpolációja bizonyos értelemben, a geometriai torzításon túlmenően, a szürkeségi értékeket is bizonyos kismértékű változtatásnak, torzításnak vetette alá. A jelen pontban tárgyalandó témáink olyan módszerek lesznek, melyek valamilyen rendszer szerint megváltoztatják a képek szürkeségi értékeit.
Tulajdonképpen ilyen módszerekkel már az analóg fotográfia is dolgozott, csak sokkal szűkebb tartományra korlátozódó vezérlési lehetőségekkel. Minden amatőr fényképész előtt ismeretes, hogy az expozíciós idő illetve a fotóanyag, valamint a hívási folyamat paramétereinek változtatásával ugyanolyan kamara és megvilágítási viszonyok esetén is különböző keménységű fényképeket lehet készíteni.
A digitális képfeldolgozás alkalmazása esetén azonban a kontrasztosságot szisztematikusan és finoman lehet változtatni. A kontraszt fokozása azt jelenti, hogy növeljük a pixelek szürkeségi értékeinek differenciáit, míg a kontraszt csökkentése csökkenti az eredeti különbségeket.
E módszereknek nagyon sok alkalmazási területe lehet, csak példaképpen említünk néhányat. Ha a kiértékelendő képpár a fényképezés pillanataiban fenálló megvilágítási különbségek következtében kölönböző keménységű, úgy mind interaktív, mind automatikus kiértékelés esetén kedvezőbb, ha először kiegyenlítjük a kontrasztjukat. Gyakran előfordul, hogy különböző véletlen hibák következtében kis kiterjedésű, az objektumtér leképzendő formáival nem magyarázható hirtelen szürkeségi érték változások lépnek fel a képen, melyek kiküszöbölése indokolt. A képkorrelációs eljárások eredményességét segíti a vonalas objektumok képeinek kiemelése az úgynevezett élkiemelés. Ez utóbbi technika alkalmazandó akkor is ha a mesterséges objektumok kiértékelését félautomatikusan vagy automatikusan akarjuk végrehajtani.
Tekintsük a pixelpontok szürkeségi értékeit megadó kifejezést diszkrét függvénynek a 2 dimmenziós térben és jelüljük sz(x,y)-al. A matematikából ismeretes (lsd. például [8] vagy [9], illetve a konkrét képfeldolgozási alkalmazásokról lsd még [10]), hogy minden periodikus függvény Fourier - sorba fejthető, ami
|
tulajdonképpen nem más, mint a 2l illetve 2k periódusú függvény helyettesítése |
|
és |
|
frekvenciájú |
harmonikus rezgések összegével. Ha a térben (vagy időben) kifejezett független változókkal rendelkező függvény nem periódikus, úgy a sorbafejtés analógiájára a Fourier transzformáltak segítségével alakítható át olyan függvénnyé, mely az eredeti függvény által leírt jelenséget a folytonos (frekvencia) spektrum segítségével fejezi ki a kétdimmenziós hullámszám (rezgészám) vektor függvényében (a hullámszám dimmenziója: 1/hosszegység, a rezgésszám dimmenziója: 1/időegység).
Ha a képfeldolgozási műveleteket közvetlenül az sz(x,y) függvény felhasználásával végezzük, úgy azt mondjuk, hogy a művelet a tér-tartományban megy végbe, ha azonban a szürkeségi függvény Fourier transzformáltjával dolgozunk, a feladat megoldását átvittük a frekvencia - tartományba. Mivel azonban végeredményként mindíg a szürkeségi függvény megváltozott értékeire van szükségünk, a frekvencia tartományból vissza kell térnünk a tér - tartományba. Ezt a feladatot az inverz Fourier transzformáció segítségével oldhatjuk meg.
A következő táblázatban megadjuk a Furier transzformáltak és inverz transzformációk képleteit folyamatos és diszkrét esetre:
|
Fourier transzformált |
inverz transzformáció |
|
|---|---|---|
|
folyamatos |
|
|
|
diszkrét |
|
|
A diszkrét esetben feltételeztük, hogy a kép n sort és ugyancsak n oszlopot tartalmaz, valamint, hogy mind a pixel koordináták (x,y), mind a hullámszámok (u,v) 0-tól (n-1)-ig egyesével változó tehát, egész értékeket vehetnek fel. Sz(u,v)-el a szürkeségi függvény Fourier transzformáltját jelöltük.
A képfeldolgozásban a Fourier transzformáltakat gyakran a konvolúció műveletének egyszerűbb végrehajtására használják fel.
A g(x,y) és f(x,y) folyamatos függvényeknek az (a,b; c,d) intervallum feletti konvolúcióját az alábbi kifejezés definiálja kétdimmenziós esetben:
|
|
, |
ahol a * a konvolúció műveleti jele. Diszkrét, kétdimmenziós esetben a sz(x,y) szürkeségi érték függvény valamint valamely másik r(x,y) képfüggvény konvolúciója  az alábbi alakot veszi fel:
az alábbi alakot veszi fel:
|
|
. |
Mivel esetünkben tulajdonképpen diszkrét sorozatok között kell a műveletet végrehajtani, célszerűbb a független változókat az elemek indexében szerepeltetni. Jelöljük az egyik képfüggvényt leíró sorozat elemeket az alábbi indexes alakkal  , a másik képfüggvény jelölése legyen hasonlóan:
, a másik képfüggvény jelölése legyen hasonlóan:  , a konvolució eredményét pedig jelölje a
, a konvolució eredményét pedig jelölje a  sorozat. E jelölésekkel a diszkrét konvolúció kifejezése a következő alakra hozható
sorozat. E jelölésekkel a diszkrét konvolúció kifejezése a következő alakra hozható
|
|
. |
Ha azonban feltételezzük, hogy a képfüggvény a kép határain túl is folytatódik, úgy az összegzési határokat, a folyamatos függvények analógiájára, a bennünket érdeklő egész tartományra ki kell terjesztenünk, azaz ebben az esetben
|
|
. |
A gyakorlatban a konvolúciót a képmátrix szűrésére is szokták használni. Ebben az esetben az r szűrő mátrix egy viszonylag kis (maximum 5x5 -ös mátrix). Ezzel a kis mátrix-szal azonban el kell végezni a konvolúciót minden képpixelre (tulajdonképpen arról van szó, hogy n x n darab tartalmában azonos, a szürkeségi érték mátrixhoz viszonyított indexeiben különböző képfüggvényünk van, s ezekkel és a szürkeségi értékek függvényével kell elvégezni a konvolúciót mégpedig olymódon, hogy minden i,j sorszámú eredeti szürkeségi érték függvény pixelhez hozzárendelünk egy megfelelő elhelyezkedésű szűrő mátrixot). Legyen a szűrő mátrix dimmenziója 2.N+1, akkor a  szűrt szürkeségi érték pixel a
szűrt szürkeségi érték pixel a
kifejezésből számítható. A Furier transzformáltak segítségével a konvolúció végrehajtása egyszerűbb, ugyanis bizonyítható, hogy
|
|
, |
azaz a konvolúció műveletét a frekvencia tartományban a megfelelő Furier transzformáltak összeszorzásával végezhetjük.
A Fourier transzformáltak konvolúcióval kapcsolatos alkalmazása mellett szólnunk kell röviden a transzformáltak fizikai tartalmáról. A transzformáltakat leíró kifejezés (lásd a táblázatban) tanulsága szerint a transzformáltak komplex számok, valós és képzetes részből állnak. A valós és képzetes részek négyzetösszegének gyökét Furier vagy frekvencia spektrumnak nevezik. Ez a mennyiség arányos a kérdéses transzformált argumentumában szereplő frekvencia amplitúdójával. A spektrum elemeinek manipulálásával lehetséges a képet alkotó frekvencia összetevők megváltoztatása, s az inverz transzformáció alkalmazásával a megváltoztatott spektrumra, optimális esetben, a kép minőségének kivánt irányú megváltoztatása. Azokra a gyakorlati módszerekre, melyekkel e javítások elérhetők a következő részben térünk ki.
E rövid matematikai összefoglalóban szólnunk kell még néhány szót a Laplace-Gauss rövidítve LoG operátorról.
A Laplace - féle operátor Descartes-féle koordináta rendszerben a következőképpen jelölhető és értelmezhető:
|
|
, |
| ahol |
 | a nabla operátor, mely valamely térbeli skalár függvénnyel megszorozva a (három) változós skalárfüggvény pontbeli |
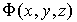 skalár függvényre alkalmazzuk a Laplace-operátort, úgy az eredmény
skalár függvényre alkalmazzuk a Laplace-operátort, úgy az eredmény
egy skalár, mely azt mutatja, hogy a  függvény változása a vizsgált pont környezetében növekszik-e vagy csökken. Ahol a függvény növekedésből csökkenésbe vagy csökkenésből növekedésbe megy át, ott a fenti kifejezés előjelet vált. Ezeket a helyeket a müszaki gyakorlat 'nullátmeneteknek' hívja. A Laplace-operátor kétdimmenziós alakját széleskörűen alkalmazzák mind a képfeldolgozásban, mind pedig a Digitális Magasságmodellel végrehajtott felület elemzésben.A szürkeségi értékek változási tendenciájának hirtelen megváltozását (növekedésből csökkenésre, csökkenésből növekedésre váltást) azonban nem csak a földi objektumok különböző fényvisszaverési tulajdonságai, hanem véletlen jellegű hatások, összefoglaló névvel a zajok is kiválthatják. Ha feltételezzük, hogy a zajok a kordinátatenglyektől függetlenek és normális eloszlásúak (lsd. pld. [3], [5], [8] vagy [9]), úgy sűrűség függvényük a következő alakban írható fel:
függvény változása a vizsgált pont környezetében növekszik-e vagy csökken. Ahol a függvény növekedésből csökkenésbe vagy csökkenésből növekedésbe megy át, ott a fenti kifejezés előjelet vált. Ezeket a helyeket a müszaki gyakorlat 'nullátmeneteknek' hívja. A Laplace-operátor kétdimmenziós alakját széleskörűen alkalmazzák mind a képfeldolgozásban, mind pedig a Digitális Magasságmodellel végrehajtott felület elemzésben.A szürkeségi értékek változási tendenciájának hirtelen megváltozását (növekedésből csökkenésre, csökkenésből növekedésre váltást) azonban nem csak a földi objektumok különböző fényvisszaverési tulajdonságai, hanem véletlen jellegű hatások, összefoglaló névvel a zajok is kiválthatják. Ha feltételezzük, hogy a zajok a kordinátatenglyektől függetlenek és normális eloszlásúak (lsd. pld. [3], [5], [8] vagy [9]), úgy sűrűség függvényük a következő alakban írható fel:
|
|
. |
A sűrűség függvényben szereplő 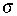 szórás esetünkben azt szabályozza, hogy egymástól milyen távol lehetnek a földi objektumok által is indokolt hirtelen szürkeségi érték változások: kis
szórás esetünkben azt szabályozza, hogy egymástól milyen távol lehetnek a földi objektumok által is indokolt hirtelen szürkeségi érték változások: kis 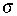 esetén közel lehetnek egymáshoz, nagy
esetén közel lehetnek egymáshoz, nagy 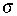 esetén csak a távoli változásokat tekintjük indokoltnak, s a szűrés csak a kép durva szerkezetét hagyja meg.
esetén csak a távoli változásokat tekintjük indokoltnak, s a szűrés csak a kép durva szerkezetét hagyja meg.
Amint már említettük, a Gauss-féle szűrővel eltávolíthatjuk a véletlen jellegű (esetleg számunkra érdektelen, egymáshoz túl közel eső) hirtelen szürkeségi érték változásokat, majd a Laplace operátorral kiválaszthatjuk a szűrt képből azokat a pixeleket, melyek környezetében a szűrés ellenére a szürkeségi értékek változásának előjelváltása továbbra is fenáll.
Nagyon sok számítási munkát megspórolhatunk azonban, ha a két műveletet egyszerre hajtjuk végre olymódon, hogy előbb képezzük a Gauss szűrő Laplace operátorát, majd ezzel a módosított szűrővel végezzük el a konvolúciót. A szakirodalom ezt módosított szűrőt nevezi LoG operátornak a Laplacian of Gaussian angol kifejezés rövidítéseként, ami magyarul úgy fordítható, hogy a Gauss-i (szűrő) Laplace-i operátora.
Az x és y szerinti második deriváltak pedig a következő alakot veszik fel:
A Laplace operátort a két második derivált összegeként kapjuk azaz
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc
|