GIS műveletek I

Ebben a részben megkezdjük a GIS műveletek tárgyalását. Először

Amint arra már többször utaltunk a Földrajzi Információs Rendszerek hátterében térbeli adatbázisok állnak. E rendszerek azonban, ahogy ezt a nevük is egyértelműen jelzi nem 'csak' adatbázisok, hanem olyan rendszerek, melyek képesek a tárolt adatokból a felhasználók igényei szerinti információt előállítani és azt szemléletes formában a rendelkezésükre bocsájtani.
Az információ létrehozásához arra van szükség, hogy az adatbázis tartalmán azaz a térbeli és leíró adatokon különböző műveleteket hajtson végre a rendszer. A közvetlenül vezérelhető műveletek összetettsége rendszerenként és utasításonként is változik, ezért célszerűbb ha a főbb műveleti csoportokat egyesek szerint GIS függvényeket tesszük vizsgálatunk tárgyává. A GIS függvény vagy művelet csoport bizonyos fokig önkényes kategória, mégis jó szolgálatot tehet a GIS-szel megoldható és megoldandó feladatok megfogalmazásában. A művelet csoportok vizsgálatánál támaszkodni fogunk azokra az ismeretekre, melyekre a korábbi részekben már kitértünk, és csak azokat a műveleteket illetve algoritmusokat fogjuk részletezni, melyekről a korábbiakban még nem volt szó. Lesznek olyan műveletek is (például formátum transzformációk), melyek alapjáról csak az egyik következő részben szólunk. Ilyen esetekben csak olyan mélységig tárgyaljuk a témát, mely nem igényli az előttünk álló részek ismeretét.

Ahogy az első fejezetben láttuk a GIS szoftverek nem egész harminc éves fejlődési szakaszt tudhatnak maguk mögött.
Különösen az első időkben minden fejlesztés speciális alkalmazások érdekében készült. Az előzőekben már kidolgozott művelet csoportokat meghagyták a következő verziókban is, de kiegészítették az újabb alkalmazások számára kidolgozott algoritmusokkal. A későbbiekben a bővítést nem csak a saját fejlesztésekkel végezték, hanem ellátták a szoftvert a mások által megoldott alkalmazások jobb vagy rosszabb implementációjával is. Ez a folyamat végül oda vezetett, hogy a vezető GIS szoftverek óriási programrendszerekké nőttek és deklarált funkcionalitásukban nagyon hasonlóakká váltak.
Ezért állítottam 1989-ben, az MTA által szervezett térinformatikai előadó napon, hogy a GIS fejlődés trendje a feladattól független, általános funkcionalitású GIS szoftver kialakulása felé mutat [4]. Bár a trend egyelőre igaznak bizonyult, ma már, hat év multán, egyre világosabb a GIS társadalom valamennyi rétegében, hogy ez az út tovább már nem járható.

A GIS ugyanis akkor tudja csak biztosítani, hogy a térbeli adatok elfoglalják az információs társadalomban az őket megillető helyet, ha beleolvad annak az intézménynek az információs rendszerébe, ahol felállításra került. Ez pedig csak akkor lehet, ha a GIS funkcionalitás csak olyan alapvető feladatokra szorítkozik mint az adat bevitel, szerkesztés, karbantartás, megjelenítés. Ebben a felfogásban a GIS a felhasználói programok inputjáról és outputjáról gondoskodik. Talán ez a jövőkép magyarázza, hogy a már ismételten tárgyalt adatmodell mellett, a szerkesztés, geopozicionálás (referencia rendszerbe kapcsolás) valamint a megjelenítés kérdéseinek szánunk különös figyelmet a következő részben.

Több GIS szoftver tartalmaz úgy nevezett 'hálózati' rutinokat forgalmi, elosztási, stb. problémák optimalizálására. Mivel nem lehet feladatunk, az operáció kutatás hálózati variánsainak algoritmikus mélységű ismertetése (ezek a matematikára esetleg a szaktudományra tartoznak) ezért ezekről a rutinokról viszonylag röviden fogunk szólni, elsősorban a bemenő és kimenő adatok kontextusában. Hasonló matematikai alapokon nyugszanak a több variánst szolgáltató 'folyosó' kijelölési eljárások, melyeket rendszerint vonalas létesítmények előtervezési stádiumában alkalmaznak. Mivel ezek az eljárások általában nem részei a szoftvernek, hanem külön felhasználói fejlesztések, részletesebb ismertetésükre a felhasználásokkal kapcsolatban térünk vissza egy későbbi fejezetben.

A jövő GIS szoftver csonkolt funkcionalitása ugyanakkor gyakran ki fog egészülni egy szakértői rendszerrel, mely tudásbázisát a kérdéses szakterület adataival kell feltölteni, míg következtető gépe általános formában kerülhet kialakításra. Ez a prognózis indokolja, hogy a jelen fejezetben röviden összefoglaljuk a szakértői rendszerekre vonatkozó legfontosabb ismereteket is.

Az alábbi csoportosításban fogunk megismerkedni a legfontosabb GIS függvényekkel:

Az adatbevitelhez kapcsolódó műveletek

Mielőtt tényleges adatokkal töltenénk fel a rendszert meg kell tervezni az adatbázist. Az adatbázis megtervezéséhez a következő szempontokat kell figyelembe venni:

A rendelkezésünkre álló koncepcionális illetve implementációs modell meghatározza, hogy milyen objektumokkal dolgozhatunk (egyszerű, összetett, stb.) illetve hogy milyen formában kell az objektumokat szervezni (alkalmazunk-e rétegeket, ha igen csak mint kisegítő eszközt vagy a síkba feszítést is feltételezi a rendszer).
Ennél a pontnál már figyelemmel kell lennünk a tervezet feladat céljaira is. Arról van ugyanis szó, hogy bizonyos fajta objektum együttest létrehozhatunk a fedvényezési eljárás (overlay) ismételt alkalmazásával is, ha az implementáció réteg jellegű és használja a síkbafeszítést. Ha tehát szükségünk lesz összetett objektumokra, úgy azokat vagy az adatbázis létrehozása előtt definiáljuk objektum orientált implementáció esetén, vagy implicit módon a rétegek kialakításával vesszük figyelembe, ha az implementáció síkba feszítés orientált.

Akármelyik implementációs modellt is alkalmazzuk figyelemmel kell lennünk a létrehozott állományok méretére. Amint azt a vektoros adatok tárolásával kapcsolatban már láttuk a grafikus adatok elérési gyorsaságát a lap szerkezet támogatja. A különböző szoftverek azonban más és más feltételeket szabnak az egyben kezelhető állományok méretére.
A kevésbé fejlett szoftverek megkívánják, hogy a betöltéskor részekre szabdaljuk az állományokat. Réteg szerkezetű implementáció esetén ezt a műveletet részekre bontásnak (tilling) nevezik. A részek nagyságára a kérdéses szoftver ad útmutatást. Logikailag a részek az engedélyezett méreteken belül vagy műveleti területenként vagy szabványos térképszelvényenként alakíthatók ki. A betöltéskor kialakított részlegek csak nehezen módosíthatók ezért ha a várható műveleteket még nem ismerjük kellő biztonsággal célszerűbb a szabványos térképbeosztás alkalmazása.
A fejlettebb szoftverek folyamatos átjárást biztosítanak az egyes rétegekben. A részekre bontást ezek a szoftverek automatikusan végzik, s így a felhasználónak nem kell gondoskodnia a partíciók kialakításáról.

A projektorientált rendszerek függetlenül az implementációs adatmodelltől igénylik a feladat megkezdése előtt a projekt területének a kijelölését. Rétegorientált rendszer esetén szükséges a figyelembe veendő rétegek megadása is.

A tulajdonképpeni térbeli adatbevitel vagy közvetlenül a GIS segítségével valósítható meg direkt módon, vagy más rendszerekből visszük át az adatokat, ezt nevezzük indirekt adatbetöltésnek.

A GIS kialakulásakor a térbeli adatnyerés szinte egyetlen módja a kézi digitalizálás volt. Ezzel magyarázható, hogy szinte valamennyi GIS szoftver rendelkezik digitalizáló modullal. Rendelkeznek ezen kívül u.n. COGO modullal, mely arra alkalmas, hogy a földi módszerekkel mért és manuálisan jegyzőkönyvezett mérési eredményeket bebillentyűzés után koordinátás állományokká alakítsa. Az újabb rendszerek rendelkeznek raszteres képek fogadási képességével is, de ez már átvezet az indirekt adatbetöltés területére.

Egy későbbi részben meg fogunk ismerkedni az archív adatbázisokkal. Az indirekt betöltés elsősorban ezeknek az előre gyártott adatoknak a betöltését jelenti. Nem hallgathatunk azonban arról sem, hogy általában nem célszerű még akkor sem a közvetlen adatbetöltést alkalmazni, ha a használt GIS rendelkezik megfelelő (digitalizáló, stb.) modullal. Amint erről már részletesen beszéltünk az automatizált földi felmérést olyan fejlett programrendszerek támogatják, melyek a mérési adatok automatizált beolvasásától a koordináta számításon keresztül az idomok megszerkesztéséig végrehajtják az automatizált digitális térképezést. Kétségtelen, hogy az automatizált térképezést szolgáló programcsomagok grafikus adatmodellje nem mindig kompatibilis a térinformatikai rendszerével, ezért még abban az esetben is, ha a kérdéses programcsomag rendelkezik a GIS által elfogadott szabványos kimenettel, célszerűbb a szerkesztést magában a GIS-ben végrehajtani.

Transzformációk, javítások, szerkesztések

Formátum transzformációk

Az archív adatok, a raszteres térképek és fényképek, a digitalizáló vagy geodéziai szoftver által szolgáltatott output formátumai általában nem egyeznek meg a felhasznált GIS szoftver saját formátumaival. Ahhoz tehát, hogy a GIS tárolni tudja az importált adatokat transzformálni kell a bevitt adatok formátumát. A formátum transzformáció képessége döntő lehet a kérdéses GIS használhatósága szempontjából.
A különböző formátumok mögött azonban adatmodell áll. Az egyszerűség kedvéért gondoljunk a raszteres adatmodellra. Egy kép formátuma általában azt jelenti, hogy egy fejezetben (header) a formátum előírásai szerint, megadjuk a kép sor és oszlop méretét, a pixel attribútumok (szürkeségi értékek) számát, esetleg a kép sarokpontjainak síkkoordinátáit, maga a formátum ezen túl úgy értelmezhető mint a pixelindexeknek megfelelő szürkeségi értékek valamely rend szerint egymásutánja, illetve a szürkeségi érték kódok milyenségének meghatározása. Ha a GIS transzformációs program ismeri ezeket a szabályokat úgy első látásra nincs akadálya a formátum transzformációnak. A valóságban azonban a megoldás csak akkor egyszerű, ha a GIS adatmodellje is képes annyi szürkeségi értéket figyelembe venni, mint amennyit a kép tartalmazott. Ellenkező esetben még a szürkeségi értékeket is át kell skálázni a GIS formátumban alkalmazott értékre.

Még bonyolultabb lehet a formátum transzformáció vektoros állományok esetén. A vektoros állományok leggyakrabban spaghetti illetve topológiai modellben kerülnek tárolásra. A spaghetti állományt gyakran alkalmazzák az automatikus térképező szoftverek, míg a GIS rendszerint topológiai modellt használ. A térképezésre gyakran használt általános rajzoló szoftver az AUTOCAD pedig a létrehozó utasítástól függően mindkét modellban létrehozhatja az alakzatokat. Ezek után világos, hogy a transzformáció csak akkor lesz eredményes ha a fogadó szoftver felismeri az importált formátum adatmodelljét és azt átalakítja a saját adatmodelljére. Ez a feladat egyértelműen megoldható, ha mind az exportáló mind az importáló rendszer egységes adatmodellel rendelkezik. Nem ilyen egyszerű azonban a helyzet az AUTOCAD esetében, gyakorlati tapasztalatok bizonyítják például, hogy nem transzformálhatók eredményesen az IDRISI-be azok az AUTOCAD DXF formátumú poligonok, melyek 'line' utasítással készültek, vagy gyakorlatilag használhatatlanok az AUTOCAD-ban azok a DXF fájlok, melyeket az ITR nevű automatikus térképező programból visznek át. Ez utóbbi program ugyanis spaghetti modellű és az átvitt sokszögek az AUTOCAD-ban is mint önálló vonalak együttesei fognak megjelenni.
Általánosítva az elmondottakat: az átviteli formátumoknak alkalmasaknak kell lenniük különböző logikai színtű adatmodellekben tárolt adatok átvitelére; az átviteli formátum fejezetében rögzített adatmodellnek megfelelően az importáló GIS-nek át kell tudni alakítania az állományt a saját grafikus modelljébe.
Ezek a kérdések megnyugtatóan csak a teljes körű szabványosítást követően oldhatók meg.

Geometriai transzformációk

Egészen más jellegű kérdések merülnek fel a geodéziai-geometriai transzformációkkal kapcsolatban. A korábbiakban megismerkedtünk a globális és a lokális referencia rendszerek fogalmával. A térbeli adatokat rendszerint valamely sík vetületi koordináta rendszer felhasználásával tároljuk. Igen célszerű, ha valamennyi adatfájl koordinátái ugyanarra a vetületi rendszerre vonatkoznak. Az esetek többségében, különösen hazánkban, azonban más a helyzet, ezért különféle transzformációk alkalmazására kerül sor az adatbázis feltöltési folyamatban.

Abban a hagyományos esetben, amikor az adatbevitelt meglévő térképek digitalizálásával végezzük, a térkép a digitalizáló tábla koordinátáiban kerül rögzítésre, mégpedig a táblára felerősített térkép tényleges tájékozásának megfelelően. Ebből először is az következik, hogy mindaddig amíg az egész térképet le nem digitalizáltuk nem volna szabad megváltoztatni a térkép tájékozását, mivel ez gyakorlatilag nehezen oldható meg a szoftver rendszerint lehetővé teszi hogy négy vagy több jól látható térképi pontot kiválasszunk s ezeket a kapcsoló pontokat minden digitalizálási munka megkezdése előtt ismételten ledigitalizáljuk. Ezeknek a pontoknak tehát kizárólag az a szerepe, hogy a térkép és a tábla kölcsönös helyzete valamennyi digitalizálási műszak során meghatározott maradjon.
Mivel a digitalizálás az adatokat a tábla koordináta rendszerében szolgáltatta, nekünk pedig sík koordinátákra van szükségünk a térkép vetületi rendszerében, újabb transzformációt kell végrehajtanunk. Ezt a transzformációt úgy tudjuk végrehajtani, hogy ismert koordinátájú pontokat digitalizálunk és egyidejűleg bebillentyűzzük ismert koordinátáikat az utasítás által kiváltott promptba. A transzformáció ebben az esetben a Helmert módszerrel történhet. A hazai kataszteri térképeken illesztőpontonként legcélszerűbb az őrkereszteket kiválasztani, a hazai topográfiai térképeken pedig a kilométerhálózati vonalak metszéspontjait. Érdemes megjegyezni, hogy az amerikai program felhasználási útmutatókban gyakran a a földrajzi koordináták (szélesség, hosszúság) metszéspontjait használják az illesztésre. Ezt azért tehetik meg, mivel a kisméretarányú földrajzi térképeken valamint egyes topográfiai térképsorozatokban a kilométerhálózat helyett a fokhálózat van feltüntetve. Gyakran előfordul (különösen hazánkban), hogy az egyes rétegek más vetületi rendszerben lettek térképezve és saját vetületi rendszerükben kerültek tárolásra digitalizálás illetve archív adatbázisból történő exportálás után. Ahhoz hogy a különböző vetületi rendszerű rétegeket közösen fel tudjuk dolgozni arra van szükségünk, hogy közös, rendszerint a hivatalos koordináta rendszerbe legyenek transzformálva.
Két különböző vetületi rendszerben térképezett fedvényt csak akkor tudunk pontos képletekkel közös rendszerbe (rendszerint a kettő közül valamelyikbe) transzformálni, ha a kérdéses vetületi rendszerek ugyanarra a dátumra vonatkoznak. Hazánkban sajnos nem ez a helyzet, és ezért a geodéziai gyakorlat koordináta tartományokra (ablakokra) érvényes közelítő képletekkel végzi a transzformációt. Bár a GIS szoftverek is tartalmaznak (hazánkra rendszerint nem érvényes) transzformációs eljárásokat egyszerűbb és indokoltabb a feladatot közös pontok felhasználásával a gumilepedő transzformációval megoldani. Erre azonban csak akkor kerülhet sor, ha a két fedvényen valóban találunk megfelelő számú közös pontot. Közös pontként azonban nem használhatók a koordináta hálózati metszéspontjai. A fokhálózati vonalak metszéspontjai is csak akkor használhatók ha a két vetület globális referencia rendszere (dátuma) azonos. Gyakran előfordul, hogy magukon a fedvényeken találunk geodéziai alappontokat, melyek koordinátái szerencsés esetben több vetületi rendszerben is nyilván vannak tartva. Abban az esetben azonban ha ezek a feltételek nem állnak fenn a transzformációt a fentebb már említett közelítő képletekkel kell végrehajtani. Ezért szükséges, hogy a szoftver szállítói ezekkel a hazai specialitásokkal bővített rendszert implementáljanak.

Javítások

Míg a szerkesztések akkor nyernek különös szerepet, ha a koordinátákat az összekötések nélkül exportáljuk, vagy a mérési eredményeket bebillentyűzve a koordinátákat a COGO modullal számítjuk magában a GIS-ben, addig a javítások mind azokban az esetekben szükségesek, amikor digitalizálással nyerjük az adatokat, vagy spaghetti modellű rendszerből topológiai modellű rendszerbe exportálunk.

 

Foglakozzunk először a javításokkal. A javításokra azért van szükség, hogy a rendszer konzisztens topológiai modellt tudjon létrehozni. A topológiai modell számára a metszéspontok és a vonalvégpontok kitüntetett objektumok, ezért azok a hibák, melyek bizonytalanná teszik a csomópont létét feltétlenül javítandók.

 
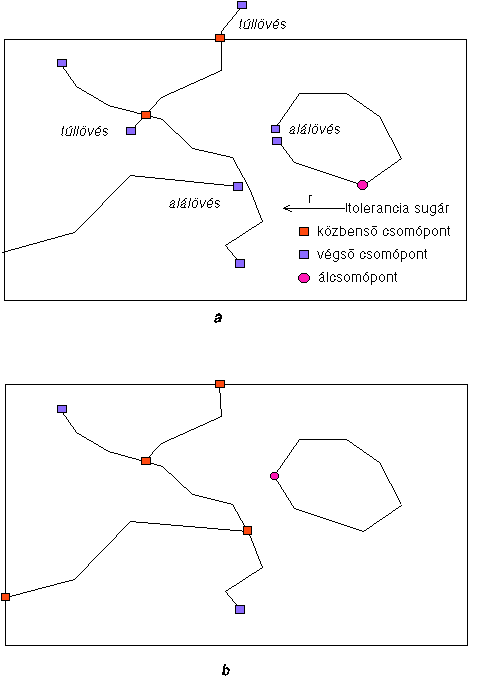
4.8 ábra - digitalizálási hibák (a) és javításuk (b)

A 4.8 ábra néhány jellegzetes digitalizálási hibát és azok javítását illusztrálja. A helytakarékosság okán eltekintettünk a síkba feszítés figyelembevételétől és ugyanazon az ábrán szerepeltettük a vonalas és területi objektumokat.

Amint látjuk, ha a metszéspontok nem pontosan a kérdéses vonalra esnek úgy két lehetőség van: vagy egyáltalán nem kereszteződik a két vonal, azaz nem jön létre közbenső csomópont, vagy túlnyúlik s ilyenkor a közbenső csomópont mellett egy végső csomópont is létrejön.

Még két másik hibát is bemutattunk: az egyik az objektum térkép szélen történő túlnyúlása, a másik pedig egy felesleges állcsomópont bedigitalizálása.

A rendszerek különféle digitalizálási stratégiát alkalmazhatnak a topológia felépítésének támogatására. A bemutatott példa azt az esetet vázolja amikor a digitalizáló személy külön billentyűvel jelzi a rendszernek a csomópontokat. A hibás billentyűzés következménye jelen esetben a zárt poligonon létrejött álcsomópont.

Ha a digitalizálás során nem kap támogatást a rendszer, vagy ami ezzel egyenértékű, spaghetti modellt importál, úgy a topológia felépítése kissé hosszabb ideig tart, de az alá és túllövések ekkor is detektálhatók.
A javítás során a szoftver a megadott tolerancia tartományon belüli hibákat automatikusan kiküszöböli. A tolerancia beállításával nagyon gondosan kell eljárnunk, mivel a hibák 'kiküszöbölése' helytelen tolerancia érték beállítása esetén az eredeti hibáknál jóval nagyobbakat eredményezhet. Ha a hibák nagyobbak a digitalizálási technikából következő értékeknél, úgy a kérdéses szakaszok digitalizálását meg kell ismételni.

Külön figyelmet érdemel a raszteres képek digitalizálásának ellenőrzése illetve javítása. A korszerű GIS szoftverek gyakran nyerik a vektoros adatokat raszteres térképek vagy ortofotó térképek képernyőn történő digitalizálásával illetve a raszteres állomány automatikus raszter-vektor átalakításával. Ebben az adatnyerési folyamatban döntő jelentősége van a vektoros ábra és az eredeti raszteres ábra egymásra vetíthetőségének. Vetített helyzetben elvégezhetjük a digitalizált sokszögvonal töréspontjainak helyesbítését (eltolás, pótlás, kihagyás, stb.), mely korrekciók általában nem igénylik a topológia megváltoztatását.
Automatikus raszter-vektor átalakítás esetén pedig szükség lehet a töréspontok interaktív ritkítására is, mely az eredeti raszter háttér megléte esetén igen hatékonyan és megbízhatóan végezhető. 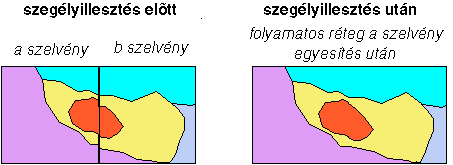Részben a digitalizálási eljárásokhoz kapcsolódik, részben a papírtérképek egyenlőtlen méretváltozásai, ritkábban a térképkészítés hiányosságai következtében áll elő az a helyzet amikor a szomszédos szelvényeken futó vonalak nem illeszkednek egymáshoz a szelvények illesztése után. Ennek a hibának a kiküszöbölésére szolgál a 'szegélyillesztés (edge - matching)' függvény (4.9 ábra).

4.9 ábra - két szomszédos szelvény szegélyillesztés előtt és után

Érdemes megjegyezni, hogy bár az utasítás hatására az eredetileg eltérő szegélymetszéspontok azonossá válnak mindkét szelvényen s igy a több szelvényből álló folyamatos állomány topológiailag korrekt lesz, helyzetileg az eltolás nem biztos, hogy javítást eredményez, hiszen nem lehet tudni hogy melyik szelvénymetszéspont milyen mértékben hibás, de azt se, hogy a szoftver milyen logika szerint tolja egymásba a pontokat.

Lényegében szintén javítási eljárás az 'egymásra illesztés (confloatation)'.
Bizonyos jellemző terepalakulatok például folyók, erdőszélek, főbb utak, stb. több fedvényen (térképen) is megtalálhatók. Mivel a térképek különböző időben, különböző technológiával s következésképpen különböző pontossági előírásokkal készülnek előfordulhat, hogy ha több térképről digitalizálunk egy réteget, vagy a későbbiekben ismertetett fedvényezési eljárást hajtjuk végre két réteg között, úgy annak következtében, hogy az azonos objektumok rétegenkínt eltérhetnek egymástól a közös rétegen az objektum többször metszheti önmagát, s a metszések következtében a valóságban nem létező poligonok jönnek létre. Ezeket a poligonokat álpoligonoknak vagy forgácsoknak (sliver) nevezik.

4.10 ábra - forgácsok keletkezése és megszüntetése

Bizonyos szoftverek biztosítják a lehetőséget az ilyen értelmű kézi vezérlésre, más szoftverek viszont az illesztést automatikusan végzik a forgácsok jellemzői (két csomóponttal meghatározott hosszukás poligonok) illetve a megadott tolerancia távolság alapján. Ebben az esetben azonban általában egyik eredeti objektum sem marad változatlan.

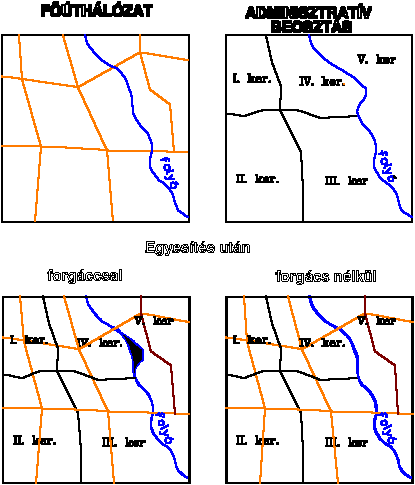
A 4.10 ábrán azt a gyakorlati esetet vázoltuk fel, amikor a folyó nem csak technikailag de tartalmilag is része mind az úthálózatot mind az adminisztratív felosztást tartalmazó rétegnek. Példánk esetében valószínű, hogy az úthálózati réteg ábrázolja a folyó aktuális képét (mivel az adminisztratív felosztás általában egy régebbi állapotot tükröz) ezért ebben az esetben indokolt az egymásra illesztést úgy elvégezni, hogy az úthálózati fedvényen ábrázolt folyó változatlan maradjon.

 

Szerkesztések - generalizálás

Más szerepet játszanak a különböző szerkesztési eljárások. Ha a geometriai adatokat a mérési eredmények bebillentyűzésével visszük be, akkor a szoftvernek lehetőséget kell biztosítania a részletpont koordináták számítására. Ha a részletpontok koordinátáit ismerjük, úgy a képernyőn a megfelelő pontok összekötésével létre kell hozni az objektumokat.
Ha a rendszerünket automatikus térképezésre használjuk, úgy további szerkesztési függvényeket alkalmazhatunk az épületek derékszögesítésére, az út egyik szélének ismeretében a másik szél párhuzamos megrajzoltatására, azonos méretű objektumok másolására, eltolására és elforgatására. Nem szabad azonban elfelejtenünk, hogy az eredeti pontok képezik a mérési eredmények által reprezentált valóságot, azaz ezeket a pontokat csak akkor szabad elmozgatni, ha valamilyen mérési vagy számítási hiba ezt indokolja.

A nagyobb térinformatikai rendszerekben általában megkülönböztetik a tárolási modellt a megjelenítési modelltől. A megjelenítési modell végső soron egy képernyő vagy papír térképet eredményez, míg a tárolási modell alkalmas a térbeli lekérdezések, elemzések végrehajtására. A két modell kapcsolata akkor válik bonyolulttá, ha arra törekszünk, hogy létrehozott adatállományból különböző méretarányú szabványos termékeket tudjunk előállítani. Természetesen nem szabad elfelejtenünk, hogy minden méretarányhoz szabványos felmérési technológia tartozik, mely meghatározza a felmérés részletességét és pontosságát. Nagyobb méretarány nagyobb részletességet és pontosságot igényel mint a kisebb méretarány s ebből egyértelműen következik, hogy míg nagyobb méretarány szolgáló felmérésből legalább is elvileg lehet kisebb méretarányú térképet előállítani, addig a fordított út még elvileg sem járható.

Ebből az alapelvből kiindulva már a digitális térképezés kezdetén azt remélték a szakemberek, hogy ha létrehozzák a nagyméretarányú digitális térképet, úgy abból tetszőleges méretarányú térképek lesznek levezethetők. Ez az elvárás a digitális térképekkel szemben különösen Európában volt nagy, ezzel magyarázható, hogy itt az USA-val szemben, először a nagyméretarányú digitális térképek létrehozásához fogtak hozzá.

Ahhoz hogy a nagyméretarányú térképből kisebb méretarányú térképet hozhassunk létre a meglévő állományokat olymódon kell ritkítani, hogy a lényeg megmaradjon, ugyanakkor fölösleges vonalak, a kérdéses méretarányban ábrázolhatatlan részletek ne terheljék a térkép áttekinthetőségét s ne növeljék az előállításához szükséges adatállományt. Ezt a bonyolult művelet sort a kartográfusok generalizálásnak nevezik.
A generalizálást több hierarchia szinten kell megvalósítani.
Az első színt azoknak az objektumoknak a megválasztása, amelyeknek a kérdéses térképen egyáltalán szerepelnie kell. Gondoljunk arra, hogy míg egy turista térképen feltüntetjük az összes földutat, turista utat, turista házat, tűzrakóhelyet, stb. a sokkal kisebb méretarányú autótérképen ezek közül csak a fontosabbak kerülnek ábrázolásra.
A második szinten az objektumok összevonása történik összefoglaló objektumokká pld. a különálló házakból tömböket alakítunk ki vagy a méretarány további csökkentése esetén a tömbökből csak a határvonalukkal ábrázolt településeket.
A következő hierarchia szinten a megmaradt egyszerű vagy összetett objektumokat vizsgáljuk meg abból a szempontból, hogy valós méreteik meghaladják-e a méretarányhoz rendelt minimumot, ha igen úgy a következő lépésben egyszerűsítünk a (kör)vonalaikon, ha nem adott méretű egyezményes jellel helyettesítjük.
A következő lépésben egyszerűsítjük a nem egyezményes jellel ábrázolt, megmaradt objektumok határvonalait, ezt nevezzük vonalgeneralizálásnak.
Mivel az egyezményes jelek általában nagyobbak mint a tényleges tárgyak méretarányban kifejezett képei ezért két közeli egyezményes jel gyakran fedheti egymást. Ezt elkerülendő, a kevésbé fontos objektum szimbólumát a generalizálás során el kell tolni.

A fenti folyamatban különös szerepe van a vonalas objektumoknak, folyók, utak, vasutak, stb. Ezek az objektumok ugyanis első lépésben egy vonallá olvadnak össze, hasonlóan ahogy ezt az egymásra illesztéssel kapcsolatban láttuk, kialakítva ily módon a tengelyvonalat, ezután kerülhet sor a vonal generalizálásra majd a generalizált vonalra illesztik az objektum egyezményes jelét.

Bár az automatikus generalizálás igénye egyidős a digitális térképkoncepció megszületésével, valóban hatékony félautomatikus programrendszerek csak az utóbbi néhány évben jelentek meg. A generalizálás teljes automatizálása vagy ahogy más elnevezéssel illetik a több méretarányú adatbázisok redundancia mentes kialakítása, egyelőre még várat magára, s a jövőben a kartográfiai szakértői rendszerek létrehozásával és a GIS szoftverekbe való beépítésével válhat valósággá.
Az ideális helyzetet azonban elég jól megközelíti a PHOCUS nevű fotogrammetriai-kartográfiai program rendszerbe integrált CHANGE nevű generalizáló program [5]. A program a következő feladatok megoldására képes:
4.11 ábra - a PHOCUS program blokkvázlata

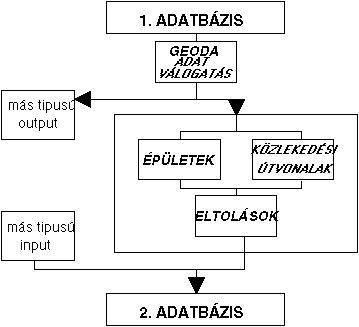
Amint azt a 4.11 ábra szemlélteti, a generalizálás megkezdése előtt ki kell jelölni a GEODA adatválasztó interfésszel az input és output adatbázisokat, és meg kell adni a generalizálás specifikációját. Látható ugyanakkor, hogy a program nincs GIS-be integrálva, s ezért használatánál nem élvezhetjük az egységes rendszer előnyeit. A GIS elemző feladatok adatelőkészítésére egyelőre azért sem alkalmas a program, mivel az attribútumok generalizálása még nem teljesen megoldott.

A hagyományos adatmodellt alkalmazó GIS-ek (vagy automatizált térképező programcsomagok) általában csak a vonal generalizálás funkcióival rendelkeznek. A funkciók megalapozását többféle algoritmus szolgálhatja. Korábban már vázoltunk egy algoritmust a raszter vektor átalakítás során keletkező töréspontok ritkítására. A jó generalizálást biztosító algoritmusokat az jellemzi, hogy a vizsgált vonal lehetőleg minél nagyobb részét igyekeznek figyelembe venni a generalizálási döntés során.

Az alábbiakban két a kartográfiában használatos vonal generalizáló algoritmust ismertetünk a [6] alapján.

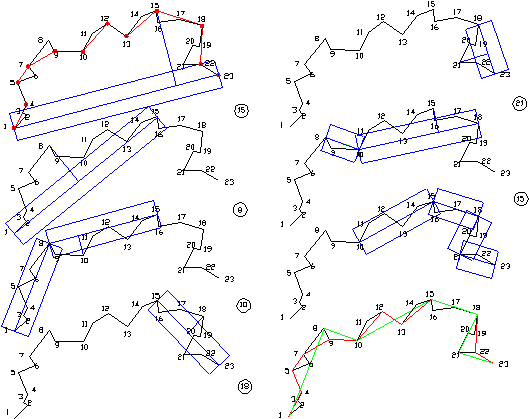
Opheim egyszerűsítési algoritmusa abból indul ki több más algoritmussal egyetemben, hogy azokat a pontokat lehet elhagyni, melyek egy-egy vonaldarabra illesztett párhuzamos egyenesek által létrehozott folyosón belül helyezkednek el. Ezen kívül még olyan kikötést is tesz, hogy a pontok nem lehetnek egy távolságnál közelebb illetve egy távolságnál ritkábban. A módszer működését a 4.12 ábra segítségével illusztráljuk.
4.12 ábra - Opheim lokális vonalgeneralizáló algoritmusa

A fölvázolt példa jól illusztrálja az algoritmus működését. Az 1 pontra az 1-2 iránnyal párhuzamosan elhelyezett folyosó a 4-5 vonalat metszi azaz a 4 pont megmarad és innen indítjuk a következő folyosót a 4-5 irányba. Ez a folyosó az 5-6 irányt metszi ezért meghagyjuk az 5 pontot - ez lesz az 5-6 irányba fektetett folyosó kezdőpontja. Ezt a folyosót a 7-8 irány metszi tehát a 7 megmarad mint a 7-8 folyosó kiindulása. A folyamat így folytatódik a vonal végéig s az egyetlen említésre való dolog a 15 ponton lép fel. Ezen a ponton ugyanis a 15-16 folyosó létrehozása után kiderül, hogy a 16 pont belül van a minimális távolságot reprezentáló körön, melyen belül elhelyezkedő túl közeli pontokat mindenképpen törölni kell. Ez arra vezetett, hogy a 16 pontot nem lévőnek tekintjük és a 15 pontra helyezett folyosót a következő 17 pont irányába fordítva folytatjuk az eljárást. Talán mondanunk sem kell, hogy a grafikus szerkesztést csak szemléltetésként mutattuk be az algoritmus valójában numerikus.

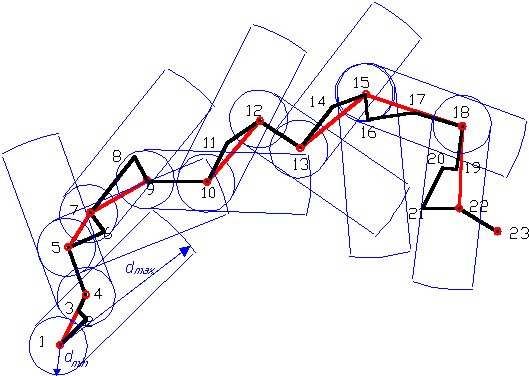
Míg a vázolt eljárás szekvenciálisan működött azaz a vonal egyik végéből kiindulva fokozatosan hajtotta végre az egyszerűsítést, az alább ismertetendő Douglas féle egyszerűsítési algoritmus globális eljárás, tehát a vonalat teljes terjedelmében vizsgálja. A 4.13 ábrán felvázoljuk az algoritmus működését.
4.13 ábra - Dougles globális vonalgeneralizáló algoritmusa

Első lépésként az előző módszerhez hasonlóan válasszunk egy tűrési sávot vagy folyosót (az ábrán kék vonalakkal határolt téglalap) - ez a folyosó úgy határozható meg, mint az első és utolsó koordináta párral definiált pontokat (példánkban 1 és 23) összekötő egyenes két oldalán fekvő t1 szélességű sáv.
Meghatározzuk, hogy melyik poligon pont derékszögű távolsága a legnagyobb a folyosó tengelyétől esetünkben ez a 15-ös, ezt a koordinátapárt egy verem első helyén őrizzük meg.
A következő lépésben új folyosót hozunk létre az 1. és 15. pont között, ekkor a 8. a legtávolabbi pont - itt a 15. pont a mozgópont. Ez az eljárás folytatódik mindaddig, amíg az összes pont a folyosón belülre nem kerül. Miután az eljárás visszajuttat a 8. ponthoz, új rögzített és mozgó pontot jelölünk ki: a 8. és a 15. (azaz az utolsó elvermelt) pontot.
E képen a Douglas-algoritmus feldolgozza a teljes vonalat, visszalépegetve addig, amíg az összes közbülső pont a folyosón belülre nem kerül és akkor kiválasztja a veremből a következő elmentett koordinátapárt.

Röviden szólnunk kell az attributív adatok szerkesztéséről is. Az attributív adatok az esetek túlnyomó többségében relációs adatbázisokban helyezkednek el. Az adatbázisok megtervezése és föltöltése általában a rendszer létrehozásának stádiumában megy végbe. Gyakran előfordul azonban, hogy a táblák oszlopait illetve sorait bővíteni kell egy egy új tulajdonsággal vagy objektummal. Hasonlóképpen gyakori eset, hogy egy egy mezőtartalmat kell megváltoztatnunk. Ezekre az esetekre a korszerű rendszerek az SQL-el kapcsolatban ismertetett eljárásokat alkalmazzák. Ugyancsak e pontban ismertettük a join műveletet is, mely segítségével azonos oszlopok alapján két táblázat összekapcsolható.
Gyakran előfordul azonban, hogy nem egész táblázatokat, hanem csak különböző táblázatokban található rekordokat kapcsolunk össze közös mező tartalom alapján. Ezt az eljárást alkalmazhatjuk például akkor is amikor a házszámokat tartalmazó utca térképhez hozzákapcsoljuk a népesség nyilvántartásból az adott utca házaiban lakók személyi adatait s ily módon a népesség nyilvántartást térbelivé alakítjuk. Sok rendszer lehetővé teszi ezt a szerkesztési műveletet, melyet a térinformatikában címillesztésnek (address matching) hívunk.
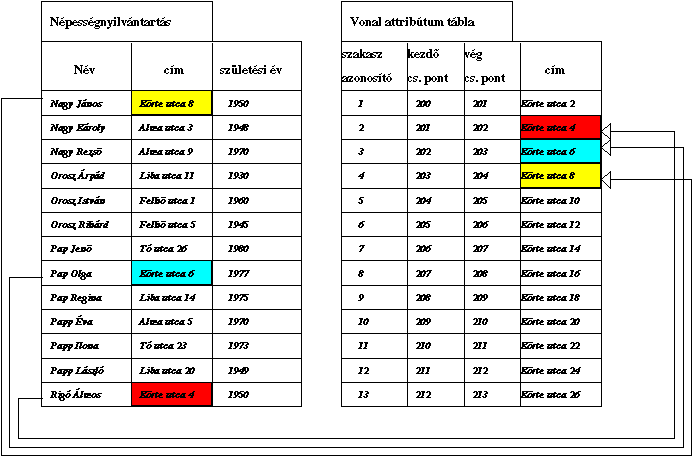
A 4.14 ábrán egy kis, leegyszerűsített részletet mutattunk be a település népesség nyilvántartását tartalmazó táblázatból valamint az utcahálózatot leíró térbeli objektumok attribútum táblázatából. Feltételeztük, hogy az úttengelyeket leíró vonalakat házszámonként (ál)csomópontokkal szakaszoljuk. Azt is feltételeztük, hogy a Körte utca elválasztott pályájú út, melyet két tengelyvonallal ábrázolunk. A címillesztés eredményeképpen az utcahálózat attribútum táblája kiegészül a címeken lakók adataival.

4.14 ábra - az utcahálózat attribútum táblázatának kibővítése

Több rendszer lehetővé teszi a címillesztés interpolálását abban az esetben is, ha az utca vonalat csak a keresztezésekben szakítják meg a csomópontok. Mivel a csomópontok attribútumként tárolják a szakaszra eső címek szélső értékeit illetve a csomópontok egymástól mért távolságát a program beinterpolálja a közbenső címek elhelyezkedését a vonalon és illeszti az interpolált címekhez a kívánt rekordokat az egyéb táblázatokból vagy kiegészíti a kérdéses táblázatokat az interpolált címek koordinátáival, azaz ellátja azokat georeferenciával. Természetesen az interpoláló rendszerek csak akkor nyújtanak térbelileg kielégítő pontosságot, ha az egy házszámhoz tartozó utcafront hosszúság azonos. Ilyen a számozási rendszer az USA-ban.

ˇ         a következő részben folytatjuk a GIS műveletek tárgyalását

ˇ         esetleg visszatérhet az előző részhez

ˇ         illetve a tartalomjegyzékhez

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc