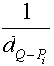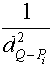Delaunay háromszögelés (tetraéderekre bontás) - Voronoi sokszögek (poliéderek)

Ebben a részben megismerkedünk

a Delaunay háromszögelés és a Voronoi sokszögek meghatározásával, az n-dimenziós algoritmussal a tesszelláció létrehozására,
a Delaunay háromszögelés és Voronoi cellák felhasználásával.

A Voronoi sokszögek, más elnevezéssel Dirichlet cellák eredetüket a matematikai krisztallográfiának köszönhetik, s ebből következik, hogy a 3 dimenziós tér 2 dimenziós redukálásával jöttek létre az évszázad elején. Napjainkban ellenkező tendencia figyelhető meg, egyre gyakrabban találkozunk az elméleti és gyakorlati irodalomban a módszer n dimenziós általánosításával.

A Delaunay háromszögelés és a Voronoi sokszögek meghatározása, n-dimenziós algoritmus a tesszelláció létrehozására

Legyenek a síkon (térben) szabálytalan elrendezésű pontjaink. Minden pont köré szerkeszthető egy olyan sokszög (poliéder), melynek belső pontjai (összes pontja a határát alkotó pontok kivételével) közelebb vannak a kérdéses ponthoz, mint az összes többi ponthoz. Az ilyen tulajdonsággal rendelkező sokszögek (poliéderek) konvexek és folytonosan töltik ki a síkot (teret). A meghatározásból következik, hogy a sokszög oldalai (a poliéder oldallapjai) merőlegesek a körülvett pontot a többi ponttal összekötő egyenesekre és felezik azokat. Természetesen nem minden sugár felező merőleges egyenes (síklap) lesz a sokszög (poliéder) része hanem csak azok, melyek metsződéseiből a zárt konvex sokszög (poliéder) létrejön. A sokszög (poliéder) oldalak egyben meghatározzák az egy-egy pontból figyelembe veendő szomszédos pontokat is, hiszen csak azok a pontok befolyásolják a sokszög kialakulását, amelyekre menő sugarak felező merőlegesei részei a sokszögnek. Ha minden pontot összekötünk a róla a fentiek szerint figyelembe veendő szomszédos pontokkal, úgy síkbeli esetben, egyértelmű és bizonyos szempontból optimális háromszögfelbontást kapunk. Ezt a felbontást nevezik Delaunay háromszögelésnek. Térbeli esetben a szomszédosként meghatározott pontok összekötése egyértelmű, optimális tetraéder felbontást eredményez.

A Voronoi sokszögek sarokpontjai, 2D-s esetben, a Delaunay háromszög csúcspontjaihoz tartozó három terület találkozási helyein találhatóak, meghatározás szerint egyenlő távolságra e három ponttól, azaz a sarokpontok a háromszögekre szerkeszthető körök középpontjai, a térben ez a tulajdonság úgy módosul, hogy a poliéderek sarokpontjai a megfelelő tetraéderekre szerkeszthető gömbök középpontjai.

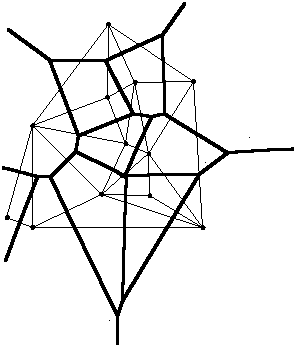
2.55 ábra - ponthalmazra szerkesztett Voronoi sokszögek és Delaunay háromszögek

Az elmondottak illusztrálására a 2.55 ábrán megszerkesztettük 12 szórt pont Delaunay háromszögelését és Voronoi sokszögeit.
Az ábrán a vastag vonalak a Voronoi sokszögeket, a vékony vonalak pedig az eredményként létrejött Delaunai háromszögelést jelölik.

Az optimális háromszögelés végrehajtására két dimenzióban igen sok algoritmus ismert. Az ismertetendő n dimenziós algoritmust A. Bowyer publikálta 1981-ben [18].

Mielőtt a számitási lépések egymásutánját meghatároznánk célszerű eldönteni a tárolás kérdését. Mivel a Voronoi cellák csúcspontjai mindíg három adatponttra rajzolható kör középpontját jelölik, célszerű e csúcspontokat e háromszög pontokhoz hozzákapcsolni. E mellett minden csúcspontnak három szomszédos csúcspontja is van, kézenfekvő, hogy ezeket a pontokat is hozzákapcsoljuk a csúcspontokhoz.

Ezek szerint minden csúcsponthoz két három elemű lista tartozik: az egyik tartalmazza a kérdéses Delaunay háromszög adatpontjait, a másik a szomszédos csúcspontokat. n - dimenzió esetén minden csúcspontnak n+1 alkotó adatpontja és n+1 szomszédos csúcspontja van.

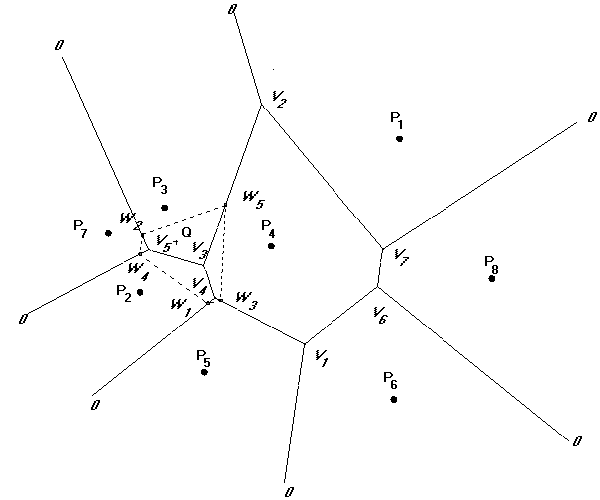
2.56 ábra - csúcspontok és háromszögek kapcsolatrendszere

Az elmondottakat 2 dimenziós esetre a 2.56 ábra segítségével illusztráljuk.

A vázolt listákat az alábbi táblázatban foglaltuk össze:

A Delaunay háromszögelést leíró listák
csúcspontok	háromszög alkotó pontok	szomszédos csúcspontok
	első második harmadik	első második harmadik
V₁	P₆ P₄ P₅	V₄ 0 V₆
V₂	P₁ P₄ P₃	V₃ 0 V₇
V₃	P₂ P₃ P₄	V₂ V₄ V₅
V₄	P₂ P₃ P₄	V₁ V₃ 0
V₅	P₇ P₃ P₂	V₃ 0 0
V₆	P₆ P₈ P₄	V₇ V₁ 0
V₇	P₁ P₈ P₄	V₆ V₂ 0

2.1 táblázat

Az ismertetendő algoritmusban nem játszik szerepet az adatpontoknak a csomópontok körüli ciklikus rendje ezért a táblázatban az egy csúcsponthoz tartozó adatpontok sorrendje tetszőleges.

Az algoritmus abból indul ki, hogy felveszi az adott dimenziószámhoz tartozó legegyszerűbb n+1 adatpont alakzatot, az úgy nevezett szimplexet, (kétdimenziós esetben egy háromszöget, 3 dimenziós esetben egy tetraédert) és a hozzátartozó Voronoi cella csúcspontot, melynek valamennyi szomszédja a végtelenben van (a végtelenben lévő csúcspontokat a 2.56 ábrán és a 2.1 táblázatban 0-al jelöltük).

Az első n+1 adatponttal szemben csak az a megkötés, hogy az n dimenziós térben nem helyezkedhet el egy hipersíkon (2 dimenziós esetben a pontok nem lehetnek egy egyenesen, háromdimenziós esetben pedig egy síkon).

Mivel kezdetben csak a legegyszerűbb alakzathoz tartozó adatpontokat vettük fel, az algoritmus feladata az lesz, hogy sorra illessze be a meglévő pontokat a felvett pontok által meghatározott konvex idomba.

A 2.56 ábrán Q-al jelöltük a beillesztendő pontot, a hozzátartozó meghatározandó területet pedig pontozott vonallal határoltuk.

Első lépésként megkeresünk egy olyan csúcspontot, mely az új adatpont megjelenésével törlődik. Ez a csúcspont bármelyik lehet azok közül, melyek közelebb vannak az új adatponthoz, mint az őket létrehozó adatpontokhoz. Egy ilyen pont mindenképpen lesz, mégpedig az ahhoz az adatpont szimplexhez tartozó csúcspont, melyen belül az új adatpont található. Példánk esetében legyen ez a csúcspont V₄. Ezután, ebből a csúcspontból kiindulva végigmegyünk a listáinkon és megkeressük a többi törlendő csúcspontot is. Először megkeressük V₄ végesben lévő szomszédját V₆-t és megnézzük, hogy alkotó adatpontjainál (P₆, P₈, P₄) Q közelebb van-e hozzája vagy sem, ezután megnézzük V₆ végesben lévő szomszédját V₂-t és a keresést analóg módon folytatjuk.

Az eljárás végén megkapjuk a törlendő csúcspontok listáját, esetünkben V₄, V₃, V₅. A törölt csúcspontok alkotó adatpontjai (P₂, P₅, P₄, P₃, P₇) közvetlenül kapcsolódnak az új ponthoz Q-hoz (azaz kétdimenziós esetben a Delaunay háromszögek, háromdimenziós esetben a tetraéderek oldalai lesznek). Azok a korábbi összeköttetések, megszűnnek, melyekhez tartozó valamennyi csúcspont törlésre került. Példánk esetében ilyen a P₂-P₄ mivel mindkét csúcspontja, melynek alkotója volt (V₄ és V₃ is) törlésre került.

Az új pont Q beillesztése öt új csúcspontot eredményezett: W₁, W₂, W₃, W₄, W₅, melyek szomszédos csúcspontjait és alkotó adatpontjait kell a továbbiakban kiszámítanunk. Minden csúcspontnál alkotó adatpontként Q-n kívül még n olyan adatpontot kell figyelembe venni, melyek Q-val össze vannak kötve. A tesszelláció minden vonalát n adatpont veszi körül pld. a V₃-V₂ vonalat P₃-P₄ alkotja. Az új csúcspontok alkotó adatpontjait és szomszédos csúcspontjait a törölt csúcspontlista nem törölt elemei segítségével határozhatjuk meg, megkeresve a körülöttük lévő adatpontok gyűrűjét. Pld. W₅ kifelé mutat Q-tól V₂ felé és P₃, P₄ és Q alkotják.

A vázolt algoritmus előnye, hogy mindig csak helyi változtatásokat végez s így egy-egy pont beillesztésének időszükséglete független a már beillesztett pontok számától. Mivel az algoritmus csak konvex idomokba való beillesztésre készült, célszerű kezdő alakzatként a ponthalmaz befoglaló alakzatát felvenni.

A Delaunay háromszögelés és Voronoi cellák felhasználása

A digitális magasságmodellek kialakulásakor, az egyszerűbb kezelhetőség kedvéért elsősorban szabályos négyzet raszterben tárolták a magassági információt. Az esetek túlnyomó többségében azonban a mérések által meghatározott magasságok nem estek egybe a rácspontokkal, ezért a rácspontok magasságát interpolációval kellett meghatározni. Közismert, hogy a közvetlen méréshez képest a legjobb interpoláció is információ veszteséggel jár, ezért már viszonylag hamar felmerült a kérdés, nem lehetne- e a modellben magukat a mért magasságú pontokat tárolni?

A válasz az volt, hogy ez lehetséges, ha megoldható, hogy az adatpontokra egyértelmű háromszöghálózatot lehessen szerkeszteni. A Delauanay háromszögelés a 80-as évek elején bevonult a magasságmodellezésbe és azóta a gyakorlatban használt programok javarésze (az un TIN programok) ezen az elven alapulnak. A háromszögfelbontás nem csak a mérési eredmények konzerválása szempontjából előnyös, hanem a különböző elemző funkciók végrehajtását is segíti. A háromszögfelbontás ugyanis a terepfelmérést végző topográfushoz hasonlóan síkháromszög lapokból álló poliéderekkel modellezi a bonyolultabb terepidomokat, s ez lehetővé teszi az esésviszonyok, benapolás, kitettség valósághű elemzését.

Az automatizált térképkészítésnél a háromszögoldalakat, a hagyományos módszerhez hasonlóan, szintvonal interpolálásra lehet felhasználni. A háromszögekre bontás nem gátolja a köbtartalom és terület számításokat sem, bár a különböző metszési feladatok végrehajtása háromszögmodellben sokkal bonyolultabb mint a négyzet raszterben. Azt sem szabad elfelejtenünk, hogy a TIN modell tárolása lényegesen nagyobb tároló hely igényű, mint a négyzet raszteré.

Míg a Delaunay háromszögelés a magasságmodellezés alapeszközévé vált, a duális Voronoi cellák e téren való alkalmazásáról csak ritkán olvashatunk. E ritka források közül Gold [19] kutatásai alapján a Voronoi cellák egy érdekes alkalmazását szeretnénk felvázolni.

2.57 ábra - a "lopott területek" módszere

Ezeket a területrészeket lopott területeknek, magát az interpoláló módszert pedig a lopott területek módszerének nevezzük.

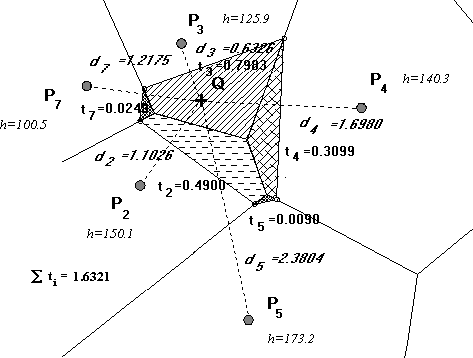
A 2.57 ábrán megismételtük a 2.56 ábra egy kis részletét.
Tételezzük fel, hogy a P_i pontok magasságát megmértük és ezek felhasználásával szeretnénk a Q pont magasságát meghatározni. Az egyik legegyszerűbb interpolálási eljárás a súlyozott számtani közép.

A szokásos modszerek súlyként az

vagy

reciprok távolságokat

illetve távolság négyzeteket használják. Sokkal kézenfekvőbb azonban ha azokkal a területrészekkel súlyozunk, melyeket a Q Voronoi cellája kimetsz a P_i pontokhoz tartozó Voronoi cellákból.

Hogy a súlyozás nem közömbös az eredmény szempontjából, azt jól mutatja a 2.57 ábra egyszerű példája. Ha a h-val jelölt pontmagasságokat a megfelelő pontnak Q-tól mért távolsága négyzetének reciprokával súlyozzuk, úgy h_Q=129.5; ha azonban súlyokként a "lopott területeket" használjuk úgy a keresett magasság h_Q=134.9. Nem szorul magyarázatra, hogy a különböző súlyozás következtében az eredmények jelentősen különböznek. Ha a terepmérés során ott választottuk a magassági pontokat, ahol jól reprezentálják a környező terepet, akkor a lopott területekkel való súlyozás nyújtja a megbízhatóbb eredményeket.

A Voronoi cellákat gyakran alkalmazzák a 2 D-s térinformatikai rendszerekben pontbeli adatforrások attribútum értékeinek síkbeli kiterjesztésére. A meteorológiai állomások hálózatára szerkesztett Voronoi cellákkal gyakran modellezik pld. a csapadék eloszlást. Az, hogy mennyivel indokoltabb ez a módszer egyéb interpoláló eljárásoknál, mindig csak a konkrét jelenség és kapcsolatrendszere együttes vizsgálata alapján dönthető el.

Napjaink geoinformációs modellezésében, kutatási szinten, egyre több figyelmet fordítanak az n dimenziós Voronoi hyperpoliéderekre. Ezek a hipertestek ugyanis alkalmasak n-3 tulajdonságérték (pld. tengeri modellek esetén sűrűség, hőmérséklet, sókoncentráció stb.) kvázi-geometriai modellezésére, s ezzel az attributiv adatok tárolásának és manipulálásának ismert geometriai alapokra való visszavezetésére. Az, hogy milyen körülmények között gazdaságos a geometriai attribútum kezelés még további elmélyült vizsgálatokat igényel.

A téma kapcsán nem árt utalni egy olyan teljesen új koncepcióra, mely a jövőben még forradalmasíthatja a 3 dimenziós térinformatikát. Ha fizikai hasonlattal élünk, a Voronoi cellákat úgy tekinthetjük, mint olyan szappanbuborékokat, melyeket a tér szórt pontjaiban egyenlő túlnyomással generálunk. A túlnyomás hatására a buborékok mindaddig növekednek, míg el nem érik egymást, és egymáshoz feszülve, folyamatosan kitöltik a pontok konvex héjával körülhatárolt térrészt. Az új koncepció buborék analógiájában a szórt pontokon különböző túlnyomással generáljuk a buborékokat s ily módon lehetővé tesszük a pontok esetlegesen különböző megbízhatósági mérőszámainak, illetve érvényességi tartományainak figyelembe vételét. Az így generált buborékok is hézag nélkül töltik ki a konvex héjat, de az eredeti Voronoi celláktól eltérő geometriával. Ennek az új geometriának a kutatását elkövetkező feladataink között tartjuk számon.