Vektoros adatmodellek tárolása
Ebben a részben megismerkedünk:
- A hierarchikus tárfelosztással,
- a címjegyzék (directory) orientált módszerekkel,
- az interpoláló hashing módszerrel,
- vonalas és területi vektor struktúrák tárolásával.
Vektoros adatmodellek tárolása
A vektoros adatmodellek nélkülözhetetlen alapelemei a pont koordináták. A pont koordináták a térbeliség legegyszerűbb vektoros kifejezői (gondoljunk pld. a geokódra), ugyanakkor a pontszerű objektumok viszonylagos egyszerűsége szemléletesebbé teheti a tárgyalásunkat. Foglalkozzunk tehát előbb a pontszerű objektumok tárolásával s ezek után próbáljuk meg eredményeinket vonalas és területi objektumokra általánosítani.
Ha a hagyományos adatszervezés eszközeivel a térbeliségtől eltekintve kísérelnénk meg a pontok tárolását, úgy a szekvenciális tárolás elveit figyelembe véve, növekvő pontszámok esetleg növekvő x vagy y koordináták szerint rendezhetnénk az adatokat. Nem igényel különösebb magyarázatot, hogy az ilyen rendezés a térbeli visszakereséseket kevéssé támogatná, a térinformatikában pedig erre van szükségünk, ezért más utat kell járnunk.
A legegyszerűbb megoldás az lehet, ha a számítógép memória területét képzeletben egy koordináta hálózattal borítjuk be és a pontkoordinátákat a nekik megfelelő tároló helyekre képezzük le (például az indirekt címzés felhasználásával).
|
|
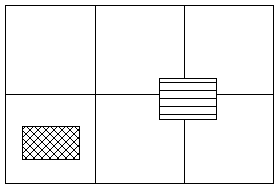
A koordináta intervallumokat realizáló négyzetháló különösen akkor előnyös, ha fizikailag is egy olyan lemez-blokkal azonosítható, melyet az olvasófej egy hozzáféréssel kiolvas. Az ilyen lemezterületeket a számítástudományban lapnak (page) nevezik. A fentiekben definiált kereső négyzetháló nagymértékben megkönnyíti hogy a szomszédos objektumok gyorsan elérhetők legyenek és módosításaik is csak helyi változásokat okozzanak a tárban. Az ábra tanúsága szerint a légelőnytelenebb esetben is csak négy hozzáférés szükséges egy négy szomszédos lapra kiterjedő pont együttes aktivizálásához. |
2.21 ábra - koordináta intervallumokat realizáló négyzetháló |
|
Vázolt koncepciónkban hallgatólagosan feltételeztük, hogy a keresőháló alapnégyzetének megfelelő tárrész (lap) konstans mennyiségű adat tárolására alkalmas. A geodéziai gyakorlat azonban arról tanúskodik, hogy a bizonyos tematikát leíró pontok sűrűsége általában nem állandó. Gondoljunk csak a földmérési alaptérképek külterületi és belterületi szelvényei közötti lényeges pontsűrűség különbségre. Ha tehát egyenlőtlen pontsűrűség esetén egyenletes keresőhálót alkalmazunk, úgy vagy a lapok egyrésze még lényegében üres amikorra más lapok már lényegében beteltek, vagy ha nem akarunk üres lapokkal dolgozni, úgy a nagyobb pontsűrűségű helyeken, a hamar betelt lapokra eső fennmaradó adatokat csak a túlcsordulási területen tudjuk tárolni, ami lényegében megnehezíti a hely szerinti visszakeresést.
A vázolt problémákat dinamikus társzervezéssel küzdhetjük le.
A dinamikus társzervezés abból indul ki, hogy egy tárrész (lap) konstans adatmennyiséget kell, hogy tároljon. Ez a követelmény viszont azzal a következménnyel jár, hogy a tárrészek különböző méretű területre eső pontokat tartalmaznak, azaz a keresőháló egyenletes beosztásából származó előnyöket elveszítjük.
Amint az egy lapra eső pontmennyiség elérte a határértéket, úgy a lap által reprezentált terület valamilyen szabály szerint felosztódik. Az osztódást fa alakú gráfokkal ábrázolhatjuk. A leggyakrabban alkalmazott negyedelést a négyágú fával quadtree-vel képezzük le.
Másik lehetőség a lapok felezéséből áll. Az úgy nevezett KD-fákkal leírható módszer alkalmazása esetén a kezdetben négyzet alakú területet váltakozva hossz illetve kereszt irányban osztjuk fel.
Mivel a raszteres adatmodellben a fa struktúrák széleskörű alkalmazásra kerülnek az ott kidolgozott algoritmusok az adott területre eső pontokat tartalmazó lapok keresésére is jól használhatók. A fa struktúrákban való keresés során egyszerűen találhatók meg a szomszédos területeket leképező lapok is, amire a 2.21 ábra tanulsága szerint gyakran szükségünk lehet.
A lapok illetve a bennük tárolt pontkoordináták a lemezegységen helyezkednek el. A lapok keresését lehetővé tevő fák leírása (pointeres vagy lineáris reprezentációja) azonban kis adatmennyiség esetén célszerűen a központi tárba kerül s ezzel a keresés jelentősen meggyorsítható. Más a helyzet, ha olyan nagy adatmennyiséget kell tárolnunk, hogy a lapokat leíró fa nem fér el a központi tárban. Ebben az esetben a lemezhozzáférések minimalizálását két alapmódszer különböző variánsainak alkalmazásával érhetjük el. Ezek a címjegyzék orientált módszerek illetve a címjegyzék nélküli hashing eljárások
.
A cimjegyzék (directory) orientált módszerek
Képzeljük el, hogy a pontokat ábrázoló területet egy olyan mátrixba képezzük le mely sorainak száma megegyezik a terület keresztirányú felbontásából származó legkisebb sávok számával, oszlopainak száma pedig a terület hosszirányú osztásából keletkező osztásközök számával. A mátrix elemei legyenek a kérdéses lapok címei. Helyezzük el ezt a mátrix alakú címjegyzéket a központi tárban. A koordináták alapján történő keresést ezután úgy végezhetjük, hogy kiszámítjuk a kérdéses mátrix elem indexét a keresett pont koordinátáiból, majd kiolvassuk a lemezegységről annak a lapnak a tartalmát, melynek címe a kérdéses mátrix elem. A lapon belüli keresés a lap szervezésétől függő keresési módszerrel hajthatjuk végre.
A fenti elvek alapján működő EXCELL módszer jobb megértéséhez tekintsük a 2.22 ábrát.
|
|
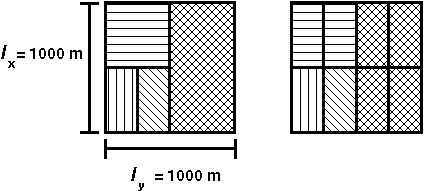
Az ábra baloldali része azt ábrázolja, hogy a figyelembe vett területre (esetünkben lx = 1000 m. és ly = 1000 m.) eső pontok tárolása melyik lapon valósul meg, azaz a baloldali ábráról leolvasható, hogy milyen koordináták tartoznak tárolás szempontjából egy laphoz. A jobboldali ábra az előbbi lapokkal felosztott terület címjegyzékbe (helyesebben címmátrixba) történő leképezése. Minden tárolt pont hozzákapcsolható a címmátrix valamely eleméhez, mely megmondja, hogy a kérdéses pont milyen cím alatt tárolt lapon található meg. A kapcsolatot a tárolt pont és a mátrix elem között ez utóbbi indexei teremtik meg, melyek a pont koordinátáiból számíthatók a baloldali képletek szerint. |
A tárolási lapokra osztott területet az EXCELL módszertől kissé eltérően képezi le a címjegyzékbe a GRID FILE módszer.
Amíg az előbbi a terület legkisebb osztásának megfelelő beosztással végig osztotta a címjegyzéket, addig a GRID FILE módszer esetén a leképezésre a következő szabályok fogalmazhatók meg:
- átmásoljuk a területi beosztást a directoryba;
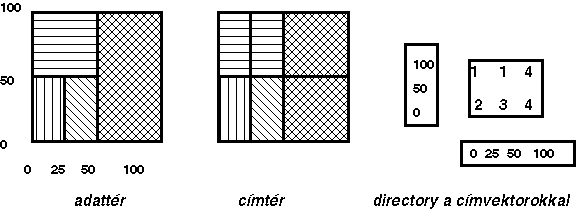
- kihosszabbítjuk a már megkezdett, de a területen végig nem húzott osztásvonalakat a címjegyzék széléig (2.23 ábra).
Ezek birtokában az indexek
kiszámítása már egyszerű feladat, csak azt kell meghatározni, hogy a kérdéses
pont x illetve y koordinátája hányadik intervallumba kerül. Az intervallumok sorszáma
szolgáltatja a címmátrix elem sor illetve oszlopindexét. Megjegyezzük, hogy a szemléletesség kedvéért a címmátrix sorindexeit a matematikában megszokott jelölésmódtól eltérően alulról felfelé növekvő rendben ábrázoltuk, szükség esetén a sorrend megváltoztatása minden nehézség nélkül elvégezhető. |
A vázolt leképezési mód azt eredményezi, hogy a címmátrix elemek indexei nem számolhatók közvetlenül a koordinátákból. Az indexek meghatározásához még két intervallum vektort is tárolni kell. |
A fenti címtár orientált dynamikus módszerek lényegében az úgy nevezett hashing módszer (hash=aprít) továbbfejlesztésének egyféle variánsai. A hashing módszer egy olyan szabványos keresési-tárolási eljárás, mely előre definiált keresési argumentum(ok) alapján történő tárolást és keresést szolgál, s egyben direkt tárelérést biztosit. A hagyományos hashing azonban statikus címjegyzékkel dolgozott, ami megkövetelte, hogy az egy hozzáféréssel kiolvasható adatok mennyiségét előre megbecsüljék, a rossz becslés vagy az esetleges törlések az egész tárelrendezés átszervezését vonták maguk után.
A dynamikus tárfelosztás igényei maguk után vonták a hashing technikák továbbfejlődését is. Ezek között találunk címjegyzéket használó és címjegyzék nélküli módszereket. Az előbbiek közé tartozik a virtuális hashing , a dynamikus hashing és a kiterjeszthető hashing . Az utóbbiak közül a lineáris hashingra és az interpoláción alapuló indexkezelésre röviden kitérünk.
A címjegyzéket használó dynamikus hashing módszerek nagyon sok hasonlóságot mutatnak az EXCELL és GRID FILE módszerekkel. E módszerekben két koordináta képezte a keresési argumentumot. Általánosan az ilyen módszereket kétdimenziós hashingnak nevezhetjük. Lehetőségünk van azonban a keresési-tárolási attribútumok dimenziójának emelésére is s így eljuthatunk a háromdimenziós hashinghoz (ennél magasabb dimenziót csak ritkán alkalmaznak).
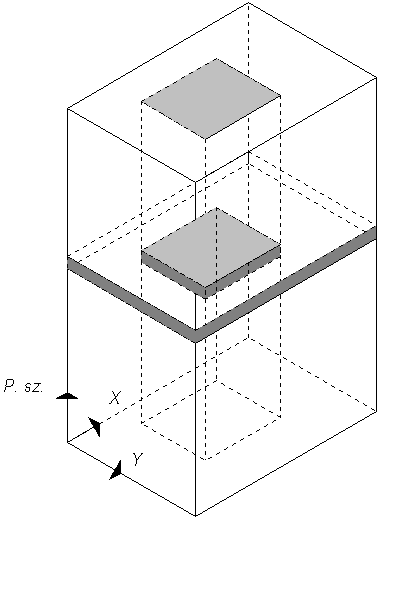
Ezek után nem nehéz kikövetkeztetni, hogy az adott pontszámú és adott koordináta mezőbe eső pontokat tartalmazó lapok címeit a lemez és a hasáb közös kockametszete szolgáltatja. |
A 2.24 ábrán a címjegyzéket egy
kockával szimbolizáltuk, mely bal alsó sarkából kiinduló derékszögű
koordinátarendszer vízszintes tengelyei az x és y koordináták szerinti, míg
függőleges tengelye a pontszámok szerinti keresési argumentumot reprezentálja
[6]. Ha
egy adott sarokponti koordinátákkal jellemzett ablakba eső pontok
koordinátáit és pontszámait keressük, úgy azokat a lapokat kell kiolvasni a
lemezről, melyek címeit az ablakra állított hasáb által a kockából kimetszett
mátrix elemek tartalmaznak. Ha egy szűk
pontszámtartományba eső pontok koordinátáira vagyunk kíváncsiak, úgy az
ezekre illeszkedő lemezzel metszve a kockát nyerjük azokat a mátrix elemeket,
melyek megadják a kiolvasandó lapok számait. |
Az interpoláló hashing módszer
Az interpoláló hashing módszer a lineáris hashing egy többdimenziós változata.
Maga a lineáris hashing azért figyelemre méltó módszer, mivel kifejezett címtár nélkül is jó teljesítményt biztosít. A módszer főbb előnyeit úgy foglalhatjuk össze, hogy
- a file növekedés és csökkenés feltételeit elegánsan biztosítja;
- nincs szüksége címjegyzék tárolására;
- a kijelölt tároló hely hasznosítása szabályozott.
Az előző pontokban a dinamikus lapkezelés tárgyalásakor abból a kézenfekvőnek tekinthető elgondolásból indultunk ki, hogy állományunk új pontrekordokkal történő bővítésekor (melyek kulcsai a koordinátákból vezethetők le) abban az esetben, ha az új rekordok beszúrása túlcsordulást idézne elő azt a lapot vágjuk ketté, melyre eső címlánc bővitése a túlcsordulást kiváltja. Ez a természetes módszer azonban csak akkor alkalmazható, ha címjegyzéket is vezetünk és tárolunk hisz a szétbontandó lapok véletlenszerűen fordulnak elő.
A címjegyzék vezetését akkor kerülhetjük el, ha a lapok felbontását szabályosan végezzük.
A lineáris hashing ezt az elvet követi mégpedig a következőképpen. Ha N számú lapunk van úgy először az 1-es lapot bontja fel 1 és N+1 lapokra majd a 2-es lapot 2 és N+2-re stb. amíg az N.-ik lapot fel nem bontja N-re és 2N-re. Ezután újra az 1-es lap kerül felbontásra 1-re és 2N+1-re s a felbontás így folytatódik mindaddig, míg ezt az új adatok fellépése szükségessé teszi.
Azt az ellentmondást, hogy az új lapok nem feltétlenül ott (azoknál a címláncoknál) keletkeznek, ahol éppen szükség volna rájuk úgy oldja fel a módszer, hogy a telítődött de még fel nem osztott lapokról túlcsorduló címekhez tartozó információt ideiglenes túlcsordulási területen tárolja mindaddig míg a szabályos osztódási mechanizmus az információ címeihez kijelölt lapot létre nem hozza. Ez azt jelenti, hogy az ellentmondás mentes állapot bizonyos késleltetéssel jön létre.
A módszerrel eredményesen oldhatók meg a rekordok beszúrásai és törlései. Beszúrás esetén a kereső algoritmus először megkeresi hogy a rekord címe melyik lap címláncába esik. Ha ilyen cím nincs még a láncban úgy megtörténik a beszúrás és a feltöltési mérőszám aktualizálása. Ha e mérőszám meghaladja a fölső határát megtörténik a lánc szétvágása. A törlés hasonlóan történik. A különbség csak abból áll, hogy itt a feltöltési mérőszám alsó határ alá csökkenése vált ki reakciót, mégpedig a két szomszédos címlánc összevonását.
Míg a lineáris hashing egydimenziós keresési-tárolási eljárás, addig az interpoláló hashing továbbfejleszti ezt a módszert k dimenziós keresésre-tárolásra azaz azokra a feladatokra, melyekkel címjegyzék orientált módszerekkel kapcsolatban már megismerkedtünk.
Az interpoláló hashing az EXCELL módszerhez hasonlóan minden lap címláncához egy keresési hálószemet (cellát) kapcsol. Ezt a módszer úgy realizálja, hogy módosítja a lineáris hashing lapbontási feltételeit. Ennek az a lényege, hogy a lap felbontásakor kettéosztja a lapra eső címláncot (azaz nem csak a túlcsorduló címek mennek át az új lapra), az eredeti lapon a kisebb címekből álló lánc marad, míg a nagyobb címekből álló lánc az új lapra kerül.
A másik sajátosság a kulcsok kialakításában van. Mivel a kulcsoknak k dimenziós keresési kritériumokat kell kielégítenie, a módszer veszi az objektum k tengely szerinti koordinátáit és egymásba tolja azokat, más szóval veszi a k darab koordináta bináris alakját és helyértékenként egymásután irja őket. A módosított lapmegosztás illetve a keresési kulcs ismertetett kialakítása azt eredményezi, hogy az interpoláló hashing az objektum tér ugyanolyan felosztását eredményezi mint az EXCELL módszer. A kölönbség mindössze annyi, hogy a keresési háló és a címláncok közötti kapcsolatot nem címjegyzék, hanem képlet szolgáltatja. További különbség, hogy a címláncok és a keresési háló között 1:1 viszony áll fent míg az EXCELL módszer esetén ez a viszony 1:sok (a címjegyzékben azonos mátrix elemek szerepelnek), továbbá az interpoláló hashing esetén a keresőháló legalább két különböző méretű elemből áll, s végül az EXCELL módszerben a kereső hálóelemek száma mindig duplázódik, míg az interpoláló hashing esetén csak eggyel nő.
Vonalas és területi vektor struktúrák tárolása
Több lehetőség is rendelkezésünkre áll amikor az eddig tárgyalt pontszerű objektumok helyett vonalas vagy területi objektumok tárolásának megoldására térünk át.
Ha a tárolás térbeliségét továbbra is szigorúan meg kívánjuk őrizni úgy az egyes objektumokat általában különböző lapokon kell tárolni (2.25 ábra).
|
|
2.25 ábra - szigorú lapstruktúra, objektumok szétdarabolása |
Ebben az esetben a különböző lapokra eső csatlakozó pontokat külön jelölni kell. A módszer akkor előnyös, ha az adatbázis többé kevésbé statikus és nem igényli a kapcsolópontok módosítását. Szigetekkel tűzdelt területi objektumoknál a módszer alkalmazása esetén problémák léphetnek fel.
Az objektum orientált programozás igényeit jobban kielégíti az a tárolási mód, amikor a geometrizált lapfelosztást csak az objektumok súlypontjaira érvényesítjük, más szóval, ha az objektumokat azon a lapon tároljuk ahová súlypontjuk esik.
Ebben az esetben a súlypontok vonatkozásában mindaz érvényes amit a pontok tárolásával kapcsolatban elmondtunk. Nem szabad azonban elfelejtenünk, hogy az objektum részletpontjait nem feltétlenül azon a lapon találjuk, amely a koordinátáikból levezethető keresési kulcsból adódik, ezért a részletpontokhoz csak az objektumon keresztül juthatunk el.
Szintén a lapokra történő direkt geometriai leképezést torzítja az átfedő lapok alkalmazása. A legnagyobb tárolandó objektum mérete ismeretében megállapítható az az átfedés, mely valamennyi objektum egy egy lapon történő szakadás mentes tárolását biztosíthatja. Az átfedés azonban azt jelenti, hogy ugyanannak a geometriai tartalomnak (koordináta párnak) több , maximum négy lap is helyet adhat, következésképpen a részletpontok tárolásakor és visszakeresésekor a koordináták mellett az objektumhoz tartozást is figyelembe kell venni a kulcsok kialakításakor.
Igen érdekes, és bizonyos szempontból előremutató a lapfelosztás fa struktúrája közbenső csomópontjainak figyelembevétele az objektumok tárolására. Amint arról már szóltunk, a fa struktúra úgy alakul ki, hogy a figyelembe veendő területet a tárolandó pontok mennyisége függvényében váltakozva hosszában illetve keresztben felosztjuk és az így kapott területrészekhez egy egy lapot rendelünk.
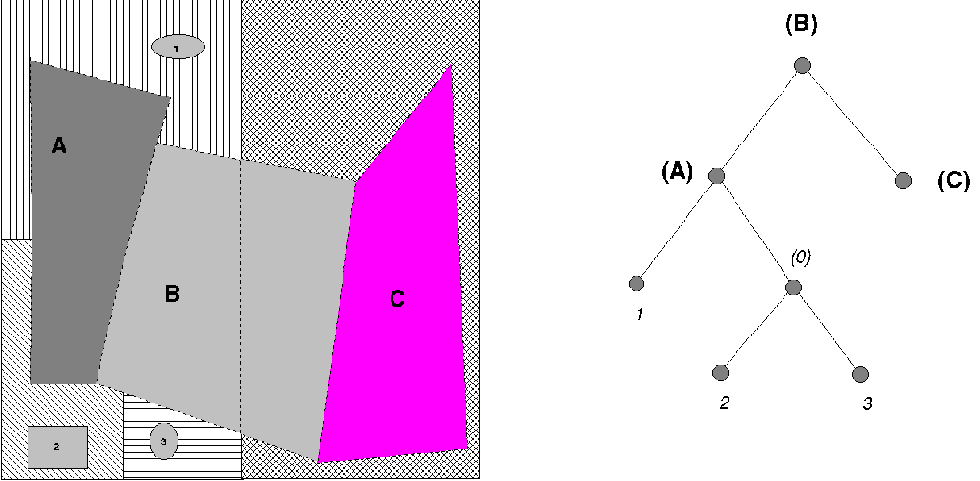
Ebben a rendszerben csak a fa levelei (azon csomópontok, melyek tovább nem ágaznak) képviselnek egy egy lapot, a közbenső csomópontok csak azt mutatják meg, hogy a levelek az eredeti terület mely részének hányszoros felosztásához tartoznak. Ha azonban a közbenső csomópontokat is tárolási funkcióval látjuk el úgy hozzájuk is kell rendelni egy egy lapot, ami a gyakorlatban azt jelenti, hogy ugyanaz a terület több lapra is le van képezve. A 2.26 ábra példáján a (B)-el jelölt gyökér csomóponthoz rendelünk egy lapot (erre tulajdonképpen az egész ábrázolt terület van leképezve), az (A)-al jelölt csomóponthoz, mely a terület bal felét képezi le szintén rendelünk egy lapot, hasonlóképpen a terület jobb felét reprezentáló (C)-el jelölt levélhez. Ezen kívül az 1, 2, 3 jelű levelekhez is tartozik egy egy lap. Az (0)-al jelölt csomópont csak elágazási funkciót végez, tehát nem tartozik hozzá lap.
|
|
2.26 ábra - közbenső csomópontok felhasználása az objektumok tárolására |
A kérdés most már az, hogy az azonos területeket leképező lapokon hogyan osztjuk el a területre eső objektumok tárolását. Mivel a fa minden hierarchia szintje egy területnagyságot reprezentál (a gyökér színt az egész területet, a következő színt a terület felét stb.) kézenfekvő, hogy a közbenső csomópontokat az objektumok területnagyság szerinti tárolására használjuk fel. A 2.26 ábra példája esetében a B objektum, mely nagyobb a terület felénél, csak az egész területet leképező lapon azaz a gyökérben kerülhet tárolásra, míg a terület negyedét meghaladó A és C objektumok a fél területeket leképező következő szinten. Hasonló módon objektum méret szerint rendelhetünk területeket az alacsonyabb csomóponti illetve levél szintekhez.
E tárolási módszer különösen előnyös a többméretarányú (multiscale) térbeli adatbázisok létrehozásában, mivel egyszerű módszereket biztosít a méretarány csökkenésével felmerülő generalizálási feladatok részbeni megoldásához. Ha ugyanis egy bizonyos méretnél kisebb objektumokat nem kívánunk ábrázolni, úgy a visszakeresésnél csak az alacsonyabb hierarchia szintekig járjuk be a fát. Természetesen a nagyobb méretű objektumok is rendelkezhetnek olyan részletekkel, melyeket az adott méretarányú ábrázolás már nem képes kifejezni. E részletek kiküszöbölésére az utóbbi időben jól működő automatizált generalizáló algoritmusokat dolgoztak ki.
ˇ a következő részben a raszter-vektor átalakítással megkezdjük a térbeli adatokkal végzett műveletek tárgyalását,
ˇ visszatérhet az előző részhez is,
ˇ vagy a tartalomjegyzékhez.
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc