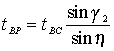Földi eljárások a pontok helyzetének meghatározására.
Ebben a részben megismerkedünk
- a térbeli helymeghatározó elemekkel, és a meghatározásukra szolgáló műszerekkel és módszerekkel,
- a magassági alapponthálózat sűrítésével,
- a vízszintes alappontsűrítési technológiákkal,
- a részletmérési módszerekkel, ezen belül
A térbeli helymeghatározó elemek, és a meghatározásukra szolgáló műszerek és módszerek
A földi vízszintes helymeghatározás két helymeghatározó elem a vízszintesre redukált szög és a vízszintesre, tengerszintre és vetületi síkra redukált távolság felhasználásával számítja ki a pont relatív vízszintes koordinátáit. Háromdimenziós földi meghatározás esetén harmadik helymeghatározó elemként a magassági vagy zenit szöget használjuk.
A helymeghatározó elemeket meg kell mérni, majd el kell látni őket a szükséges redukciókkal.
A szögek vízszintes vetületeinek a megmérésére a teodolitok szolgálnak. Ugyancsak a teodolitok segítségével mérjük az irányok magassági vagy zenit szögeit.
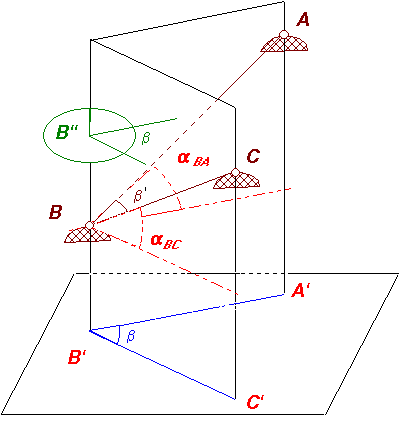
A 3.7 ábrán szemléltetjük sematikusan a teodolit működési elvét. A B terepi pontról szemlélve az A és C terepi pontok ß' szöget zárnak be egymással. Számításainkhoz azonban nem a térbeli szögre, hanem a vízszíntes síkba vetített ß szögre van szükségünk. A teodolitot úgy konstruálták, hogy ezt a szöget mérje.
Ezt úgy valósítja meg, hogy a műszer álló tengelye körül, mely helyesen felállított műszer esetén a B ponton átmenő függőleges meghosszabbításában helyezkedik el, egy forgórész az u.n. alhidádé forgatható. Az alhidádéra erősített fekvő tengely körül pedig a távcső forog a függőleges síkban.
|
Az álló tengelyre merőlegesen egy osztott
kört helyeznek el ezt nevezik limbusznak, mely az alhidádé forgása
közben mozdulatlan helyzetet foglal el. Az alhidádéra mereven szerelt index
az alhidádéval együtt forog az osztott kör fölött. Ha a távcsőben elhelyezett
szálkereszttel beirányozzuk a C pontot , úgy az index
felhasználásával leolvasást tehetünk a vízszintes körön, nevezzük ezt a
leolvasást lC-nek. Hasonlóképpen az A pont beirányzása után
leolvashatjuk lA-t. Nem szorul különösebb
magyarázatra, hogy a vízszintes körön tett két leolvasás különbsége a
térbeli szög vízszintes síkba vetített értéket szolgáltatja, azaz |
|
Mint már említettük a teodolitok alkalmasak a magassági és zenit szögek meghatározására is. Ezt az teszi lehetővé, hogy a fekvőtengelyre egy magassági kört ékelnek, melyen egy vízszintes helyzetű indexen lehet leolvasást tenni. A magassági és zenit szög közötti összefüggést a 3.8 ábra szemlélteti, e
|
Nagyon lényeges megjegyeznünk, hogy a magassági szög és a vízszintes szög között nem csak az a különbség, hogy az első a függőleges a második pedig a vízszintes síkban helyezkedik el, hanem az is, hogy a magassági szög abszolút érték abban az értelemben, hogy egyik szárát mindig a vízszintes alkotja, míg a vízszintes szög relatív érték hisz két szára tetszőleges irány vízszintes vetülete lehet. |
|
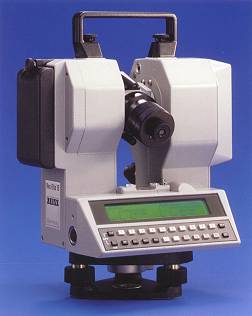
A teodolitok igen bonyolult, szabatos,
optikai, finom-mechanikai műszerek, a legkorszerűbb un. elektronikus
teodolitok e mellett még mikroprocesszorokkal és mágneses adattárolókkal is
el vannak látva. |
|
|
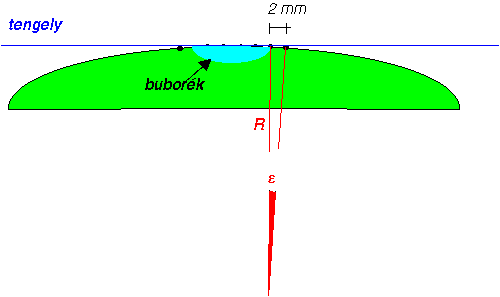
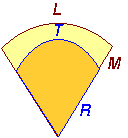
A libella palástja hosszmetszetben kör,
melyen 2 mm. hosszú osztások találhatók. Ha egy osztás két végpontjából
meghúzzuk a hosszmetszetként jelentkező kör sugarait azok metszéspontja
kijelöli a kör középpontját illetve a szabványosan 2 mm hosszű osztáshoz
tartozó középponti szöget. Ezt a szöget nevezik a libella állandójának
és általában |
A vízszíntes illetve függőleges helyzetek létrehozására a teodolitokban libellákat és ingás kompenzátorokat alkalmaznak. A libella elvileg azonos a minden háztartásban és különböző iparágakban (építőipar, asztalosipar stb.) sokszor használt "vízmértékkel". A különbség csak az, hogy a műszerekben használt libellák szabatos kivitelűek és sokkal érzékenyebbek a háztartásokban használtaknál. A libellák érzékenysége a szabatos kivitel mellett állandójuktól függ. |
Az utóbbi évtizedek legjelentősebb műszerfejlesztései a másik helymeghatározó elem a távolságok megmérésének tökéletesítésére irányultak. A fizikai vagy más elnevezéssel elektronikus távmérés csak a 60-as évek második felétől kezdte meg diadalútját a gyakorlati geodéziában. Napjainkban már nem képzelhető el semmilyen terepi munka elektronikus távmérő berendezés nélkül. Meg kell azonban jegyeznünk, hogy önálló távmérő berendezést napjainkban már alig használnak: a távmérőt vagy ráhelyezik a hagyományos teodolitra, vagy ma már gyakrabban, az elektronikus teodolittal egybeépítve mint a mérőállomás egyik funkcióját használják.
A távmérés elve nagyon egyszerű. Felállítják a távmérőt a távolság egyik végpontján majd a műszer távcsövén keresztül modulált infravörös fényt bocsátanak ki a távolság másik végpontján található visszaverő prizma felé. A fényt a visszaverődés után a távcső a vevő fotodiódára fókuszálja. A fotodióda elektromos jellé alakítja a vett optikai jelet és fázisát összehasonlítja az éppen kibocsátásra kerülő jel fázisával. A fáziskülönbség a moduláló frekvencia nagyságától függően távolság értékké transzformálható. Ha a mérő frekvencia annyira alacsony, hogy a mérő hullám hossza nagyobb mint a távmérő hatótávolsága úgy a transzformált fáziskülönbség egyben a távolság nyers értéke is. Ha azonban a nagyobb felbontás, tehát nagyobb pontosság érdekében rövidebb mérőfrekvenciát alkalmaznak akkor a távolság meghatározásához több, különböző mérőfrekvencián végrehajtott fáziskülönbség mérésre van szükség. (A gyakorlatban két megfelelően választott mérőfrekvencián mérik a fáziskülönbséget, ezen kívül megmérik hogy hányszor fordul elő nulla fáziskülönbség a közben amikor az egyik mérőfrekvenciáról folyamatosan a másik mérőfrekvenciára hangolnak).
A vázolt nyers eredmény azonban még további finomításokra szorul. A jelenleg használatos műszerek mind az alapmérést mind annak bizonyos korrekcióit automatikusan végzik, bizonyos korrekciókat viszont csak akkor képesek figyelembe venni a számításban ha megkapják hozzá az operátortól a szükséges inputot. Vannak műszer típusoktól függően különböző olyan korrekciók is melyeket az operátornak kell a műszertől függetlenül kiszámolnia.
Minden korszerű műszer automatikusan figyelembe veszi az u.n belső út méréséből adódó korrekciót valamint a mechanikai konstrukcióból adódó esetleges külpontosságot. Az operátorra vár azonban valamilyen mértékben a prizma-állandó figyelembe vétele. A fejlettebb, menü vezérelt rendszerek (ilyenek általában az u.n. teljes mérőállomások) megkérdezik az operátortól a prizma állandó értékét, a régebbi mikroprocesszoros rendszereknél nehezen hozzáférhető mikrokapcsolókkal lehetett beállítani az állandó értékét, az egyszerű távmérőknél az operátornak önállóan kell elvégezni a korrekciót.
Az elektromágneses hullámok, így az infravörös fény terjedési sebessége is függ a levegő törésmutatójától. Mivel a fáziskülönbség hosszá alakítása szintén az aktuális terjedési sebesség függvénye, így a mért távolság is természetesen függ a törésmutatótól. A törésmutató figyelembe vételéhez meg kell mérnünk az irányvonalra átlagosan jellemző hőmérsékletet és légnyomást. A gyakorlatban általában elég, ha az álláspont környékén kiválasztunk egy árnyékos és szellős helyet és ott végezzük a mérést. A mért hőmérséklet és légnyomás értékeket menüvezérelt rendszereknél csak be kell billentyűzni a műszerbe, a hatás figyelembe vétele automatikusan történik. Mind a korábbi mikroprocesszoros műszereknél mind a közönséges távmérőknél a mért hőmérséklet és légnyomás értékekből egy nomogramm tárcsa felhasználásával az operátornak kell meghatározni a beállítási értékeket, melyeket vagy mikrokapcsolókon vagy forgatható gomb körskáláján kell beállítani a mérés megkezdése előtt.
A távmérő műszerek a d ferde távolságot mérik, míg számításainkban mindig a vízszintes távolság, t szerepel. A redukció egyszerűen számítható mivel
![]() .
.
A teljes mérőállomások általában rendelkeznek olyan funkció-gombbal, mely
lenyomás esetén a vízszintes távolságot szolgáltatja. Mégis az automatizált
feldolgozás során rendszerint a ferde távolságot és a zenitszöget rögzítjük és
a redukciót a feldolgozó programmal végeztetjük. A tulajdonképpeni távmérők
(néhány külön kompenzátorral ellátott típus kivételével) nem képesek elvégezni
a vízszintesre történő redukálást ezért ezt vagy az operátor vagy a feldolgozó
program kell, hogy végezze. Ehhez azonban meg kell mérnünk teodolittal az
irányzott prizmára menő irány zenitszögét. Ezért kényelmetlen a mérés, ha a
távmérő független a teodolittól.
Bármilyen műszerrel is dolgozzunk a tengerszintre való redukciót magunknak illetve a feldolgozó programnak kell elvégeznie. A 3.12 ábra alapján felírhatjuk,
|
hogy |
|
illetve azonos átalakítások után |
|
|
, és mivel M értéke R-hez képest elhanyagolhatóan kicsiny |
|
(R=6370 km.) a tengerszintre történő redukció az alábbi kifejezésből számítható:
|
||
3.12 ábra - a
tengerszintre redukálás elemei
|
Általában nem hagyhatjuk figyelmen kívül vetületi korrekciót sem, mellyel minden esetben a feldolgozási fázisban kell a mérési eredményeket korrigálnunk. A redukció képlete a lokális referencia rendszertől függ, ha az EOV rendszerben dolgozunk, úgy az előző részben közölt képlet alapján végezhetjük a számítást.
Konstrukció szempontjából a távmérők három nagy csoportra oszthatók. Az önálló távmérők villás foglalattal helyezhetők a hüvelyes műszertalpba (ugyanabba a műszertalpba, melybe a teodolit is helyezhető), az irányzást dioptra és távcső szolgálja. A legtöbb távmérőt a teodolitokkal kombináltan használják. A rátét távmérőket megkülönböztetjük a szerint, hogy a teodolit oszlopaira vagy a távcsövére vannak-e szerelve. Az első esetben a konstrukció masszívabb, kevésbé károsítja a teodolitot, hátrányos viszont, hogy mind a teodolittal, mind a távmérővel külön kell irányozni. A távcsőre szerelt műszerekkel elvileg egyszerűbb a mérés, hátrányuk ugyanakkor, hogy rongálják a fekvőtengely csapágyait valamint, hogy igen gyakran elállítódik a távcső és a távmérő párhuzamossága, ami azzal jár, hogy a műszerrel egyáltalán nem lehet távolságot mérni. A legkorszerűbb konstrukciók közös neve a teljes mérőállomás (total station) a típus másik kevésbé reklámízű elnevezése: elektronikus regisztráló tahiméter.
|
|
A műszer tulajdonképpen egy elektronikus teodolit, egy távmérő, egy mikroprocesszor, egy adatrögzítő és egy programrendszer kombinációja. |
Vannak típusok, amelyekben a távmérőt beépítik a teodolit műszerházába (pld. a 3.13 ábrán látható RegElta esetében), más típusoknál a távmérő ráépül a távcsőre (nem felette van mint a rátét távmérő, hanem körbeveszi). Hasonlóképpen az adatrögzítő is lehet beépített vagy különálló, a műszerhez kábellel kapcsolódó egység. A gyakorlati munka szempontjából a beépített adatrögzítő sokkal előnyösebb (újabban már nem is gyártanak mást).
A geometriai adatgyűjtéshöz kapcsolódó feladatok szempontjából még két fontos távmérő paraméterről kell szólnunk: a hatótávolságról és a pontosságról. Célszerű olyan távmérővel dolgoznunk, mely 2-2.5 km.-ig mér. Azok a távmérők, melyek csak 1 km.-ig illetve 1.5 km.-ig mérnek sok feladat megoldását megnehezíthetik. Pontossági szempontból nem kell ilyen igényesnek lennünk mivel a korszerű távmérők lényegében két pontossági osztályba tartoznak. A pontos távmérők rövid távolságon 0.2 mm. pontosságúak, korszerű 'közönséges' távmérőknél ez az érték 2.0 mm. Céljainkat teljesen kielégíti az utóbbiak pontossága, sőt pontossági szempontból megfelelnek azok a régebbi távmérők is melyek hibája 5 mm körüli érték volt.
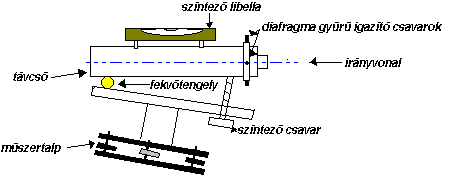
Ha figyelemmel vagyunk az alappontok térbeli elhelyezkedésére, úgy két pont magasságkülönbségét is helymeghatározó elemnek tekinthetjük. A magasságkülönbségek szabatos meghatározására szolgáló műszert szintező műszernek nevezzük. A szintező műszer elvi vázlatát a 3.15 ábra tartalmazza.
Ha ugyanis a szintező libella tengelye párhuzamos az irányvonallal (a szálkereszt metszéspontján és az objektív optikai középpontján átmenő egyenessel), úgy a szintező csavar segítségével a beosztás közepére hozva a szintező libella buborékát az irányvonal vízszintes lesz azaz érinti a szintfelületet. |
A szintező műszer olyan optikai finommechanikai műszer, mely lehetővé teszi valamely pontban a szintfelület érintősíkjának kitűzését. |
|
A műszerrel magasságkülönbséget úgy határozhatunk
meg, ha a 3.16 ábrán látható elrendezés szerint két függőleges helyzetű
osztott lécet helyezünk el a műszertől egyenlő távolságokra lévő pontokon és
a léceken tett leolvasásokat kivonjuk egymásból.
|
és a Q pont magassága a P pont felett a
kifejezésből számítható. |
Az egy álláspontból irányozható pontok azonban nem lehetnek egymástól messze mivel a d műszer-léc távolságok nem haladhatják meg mérnöki szintezés esetén a 100 métert, szabatos szintezés esetén pedig a 40 métert. Mivel a meghatározandó alappontok ennél mindig messzebb vannak egymástól ezért a bemutatott képlettel meghatározható magasságkülönbség csak olyan helymeghatározó elemnek tekinthető melyet a különböző színtezési technológiák a magassági alappont sűrítésre felhasználnak.
A szintező műszerek osztályozását két szempontból végezhetjük, ezek a pontosság és a működési elv.
Az első osztályozási szempont alapján megkülönböztetünk mérnöki szintezőket és szabatos szintezőket.
A második szempont szerint a műszerek három alapvető típusát említhetjük, ezek a libellás szintezők, kompenzátoros szintezők, és az automata elektronikus szintező.
A libellás színtezőkben az irányvonalat a színtező libella felhasználásával tesszük vízszíntessé. A különbözô konstrukciók abban a módban különböznek ahogy a libella középhelyzetét az észlelő szemlélheti ( tükörből, az okuláris melletti mikroszkópból, a látómezőbe bevetített ablakból). Napjainkban libellás színtezőket már nem gyártanak, de mivel általában tartós konstrukciók még jó néhány évig előfordulhatnak a gyakorlatban.
|
|
A kompenzátoros szintezők irányvonalát valamely ingás optikai-mechanikai szerkezet automatikusan vízszintes helyzetbe hozza (illetve az észlelő számára indifferensen, azonos leolvasást eredményező módon vetíti a vízszintes fősugarat a vízszintes szálra), ha a műszer állótengelyét az észlelő közel függőleges helyzetbe hozza. |
A csoport előnye abból ered, hogy sokkal gyorsabban lehet létrehozni a közelítő függőleges helyzetet, mint az érzékeny szintező libellát középre hozni.
Az első Na 2000 típus jelű automata elektronikus szintezőt 1990-ben bocsátotta ki a svajci Wild gyár, a korszerűsített műszer típus jele Leica Na 2002. A műszer azzal könnyíti meg az észlelő munkáját, hogy a lécleolvasást automatikusan végzi. Az észlelő a három talpcsavar segítségével közel függőleges helyzetbe hozza az állótengelyt majd beirányozza a vonalkóddal ellátott szintező lécet és megnyom egy gombot. A lécleolvasás 4 másodperc múlva megjelenik a műszer kijelzőjén és a lécleolvasás és műszer-léc távolság jegyzőkönyvezhető, illetve adatrögzítőben tárolható. Bár a műszer jelentős lépés a szintezési technológia automatizáltsági szintjének közelítésében a vízszintes mérési technológiákhoz, szélesebb elterjedését több körülmény is gátolja.
Elsőnek említhetjük a technológia kiforratlanságát ami abban nyilvánul meg, hogy nem elég magát a kérdéses leolvasást szabadon irányozni, hanem mivel a leolvasás automatikus kialakítása az irányvonal alatt és fölött 1-1 fokos látószögnek megfelelő léctartomány kiértékelésével történik, legalább is elvileg, e tartományban sem lehet takarás. A svéd geodéták vizsgálatai szerint elég, ha a kérdéses lécfelület 70 százaléka takarás mentes. Nagyobb takarás esetén azonban 1 mm.-es hiba is lehet a leolvasásban anélkül, hogy a műszer ezt jelezné. Valószínű, hogy a gyártó e tapasztalatok figyelembe vételével úgy fogja továbbfejleszteni a műszert, hogy az a túlzott takarás esetén hibaüzenetet adjon.
A kombinált vízszintes és magassági részletmérés gazdaságosabban végezhető elektronikus tahiméterekkel mint elektronikus szintezőkkel, ezért a szintezési technológiák alkalmazása jelentős mértékben visszaszorult a magassági alappont meghatározás és alappont sűrítés területére. Ezek a feladatok különösen a magassági alappont hálózat létrehozása illetve karbantartása viszont igen kényesek a pontosságra. Ezért az automata elektronikus szintező felhasználási területe eléggé leszűkült és nem áll arányban a műszer viszonylag magas árával.
A másik osztályozási szempontot vizsgálva, a szabatos szintezőknek azokat a szintezőket nevezzük, melyek libellája (kompenzátora) nagy érzékenységű (beállási középhibája 0.05"-0.1"), távcső nagyítása 30-50 szeres, speciális leolvasó-berendezése segítségével 0.01 mm élességű leolvasásra alkalmas különleges invár-betétes lécek alkalmazása esetén. Az általunk vizsgált feladatok általában nem igénylik szabatos szintezők igénybevételét.
Színtezési feladatainkhoz a magassági alappont sűrítés területén mérnöki színtezőket célszerű használnunk. E műszertípust az alacsonyabb libella (kompenzátor) beállási pontosság (0.3"-0.5"), a kisebb távcső nagyítás (28 -32) és a közvetlen lécleolvasás jellemzi. Ez utóbbi azt jelenti, hogy a lécen a centimétereket fekete-fehér kockákkal jelölik és az észlelőnek meg kell becsülnie, hogy a vízszíntes szál a kockát hanyadrészben metszi.
A magassági alappont hálózat sűrítése
A lokális magassági referencia rendszer pontjai bár a lokális vízszintes referencia rendszer pontjaival azonos sűrűséggel kerülnek meghatározásra egyelőre fizikailag nem esnek egybe az utóbbiakkal. Ugyanakkor a térinformatikai rendszerek feltöltésekor az esetek többségében szükségünk van a felmért részletpontok magasságára is. Mivel a felmérésekhez rendszerint a vízszintes alappont hálózatot is sűríteni kell és a sűrítést mindig a meglévő alappontokra támaszkodva kell végrehajtani kézenfekvő, hogy a magassági alappont hálózat sűrítését azoknak a vízszintes alappontoknak a szintezésével kezdjük, melyeket a felméréshez, illetve az azt megelőző vízszintes alappont sűrítéshez felhasználunk. Az esetek többségében a további magassági sűrítést, a felméréshez hasonlóan, az elektronikus tachiméterek segítségével a trigonometriai magasságmérés módszerével végezzük.
Az alappont színtezés olyan magassági alappont sűrítési technológiák összefoglaló elnevezése melyek valamelyikének kiválasztásával adott hibahatárokon belül meg tudjuk határozni két egymástól egy műszerállásnál nagyobb távolságra fekvő pont magasságkülönbségét.
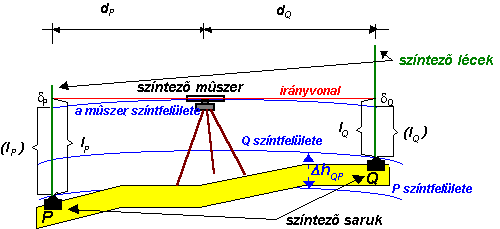
Az első problémánk tehát a 3.16 ábrán vázolt elrendezés kiterjesztése arra az esetre amikor a meghatározandó magasságkülönbség végpontjai egy műszerállásból már nem szintezhetők. Ez a helyzet vagy azért áll elő mert a két kérdéses pont távolsága (az összelátási viszonyok figyelembe vételével) nagyobb mint 200 m. mérnöki szintezés illetve 80 m szabatos szintezés esetén, vagy azért mert a két pont között olyan nagy a magasságkülönbség, hogy a pontoktól egyenlő távolságra felállított műszer vízszintes irányvonala az egyik léc alá és/vagy a másik léc fölé "lő". A megoldást a 3.19 ábra szemlélteti.
|
Az ábrán t1 -el jelölt
pont az úgy nevezett kötő pont, melyre csak a magasságkülönbség
továbbadása szempontjából van szükségünk, ezért maradandóan nem
állandósítjuk. |
Mérnöki szintezéskor a kötőpontokra gömbölyű fejű öntöttvas idomtestet u.n. szintező sarut helyezünk, melyet a léchordó segédmunkás a lécre történt második (hátra) észlelés után felemel és magával visz. Szabatos szintezésnél az egész szintezési szakaszt kicövekelik, a műszerálláspontokat egyszerű cövekek, a lécpontokat gömbölyű fejű szöggel ellátott cövekek jelölik. |
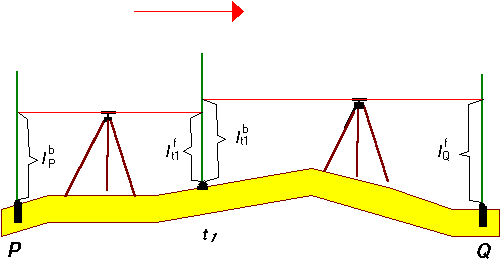
A mérést a P ismert ponton kezdik, melyre elhelyezik az első szintezőlécet. Kiválasztják az első műszerálláspontot olymódon, hogy róla a léc irányozható legyen és ne legyen messzebb P-től mint az adott pontossági osztályra jellemző műszer-léc távolság (100 m mérnöki szintezés, 40 m. szabatos szintezés esetén), e mellett arra is figyelemmel kell lenni hogy a műszer léc távolsággal megegyező távolságra a szintező saruval jelölt t1 kötőpont a lécleolvasás szempontjából megfelelő magasságban kitűzhető legyen. Az első műszerállásban elvégzik a szintezés haladási értelmében "hátra" leolvasást a P ponton felállított lécre, majd az "előre" leolvasást a t1 kötőpontra. Ezután a műszer és a hátsó léc tovább megy. A műszer az új álláspontra a léc pedig a Q pontra. Az észlelő elvégzi a "hátra" leolvasást a t1 kötőpontra és az "előre" leolvasást a Q pontra. Ha a vonal tovább folytatódna a t1 pontról segédmunkás továbbvinné a sarut és lécet a következő kötőpontra és ez mindaddig így folytatódna amíg az állandósított végpontot el nem érik. A Q végpont P kezdőpontra vonatkozó magasságkülönbsége ezek után az alábbi kifejezésből számítható:
![]() ,
,
ahol P és Q a szintezés kezdő és végpontját, n a műszerálláspontok számát, lji pedig a lécleolvasásokat jelöli.
A szintezést a különböző hibahatások csökkentése érdekében
általában mind oda mind vissza értelemben végrehajtják. Mivel az oda-vissza
értelemben szintezett vonal zárt vonalnak tekinthető (kezdő és végpontja
azonos) az oda és vissza szintezett magasságkülönbségek összege nullát
kellene hogy adjon. A mérési hibák következtében azonban az összeg
rendszerint nem egyenlő nullával. A nullától való eltérést az oda-vissza
szintezés záróhibájának nevezzük. Mérnöki szintezés esetén a
záróhiba megengedett értéke ![]() mm. Szabatos szintezés
esetén a megfelelő hibahatárt a
mm. Szabatos szintezés
esetén a megfelelő hibahatárt a ![]() mm. kifejezés szolgáltatja. K
a zárt vonal hossza kilométerben.
mm. kifejezés szolgáltatja. K
a zárt vonal hossza kilométerben.
A térinformatikai rendszerek feltöltésénél a legpontosabb magassági adatokat a nagyméretarányú mérnöki felmérések digitális variánsai igénylik. E feladatok előkészítése során általában mérnöki szintezéssel határozzák meg a vízszintes sűrítéssel létrehozott új alappontok magasságait. Kisebb pontossági igényű esetekben a magassági alappontról kiinduló szintezéssel csak néhány új alappont magasságát határozzák meg, a többi új alappont magasságának meghatározásához a trigonometriai magasságmérés módszerét veszik igénybe. Ez azzal az előnyel jár, hogy a mérést ugyanazzal a műszerrel - elektronikus regisztráló tahiméterrel végezhetik mint magát a felmérést. E mellett még megemlíthetjük, hogy ez a módszer sokkal gyorsabb és kényelmesebb mint a szintezés. A módszer hátránya a kisebb pontoság, bár megfelelő technológia esetén 1 - 2 km.-es távolságig elérhető, hogy a hiba ne haladja meg jelentősen a mérnöki szintezés hibáját.
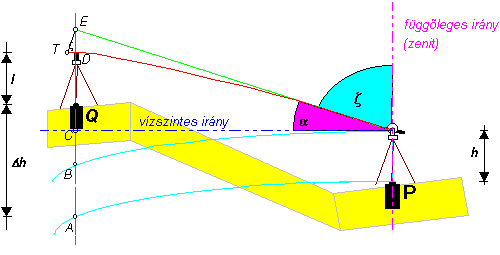
az ED távolság maradt, mely az általában ismeretlen földközeli fénytörés (refrakció) hatására jön létre. Ha feltételezzük, hogy a
a Föld görbületi sugara, R' pedig a refrakció görbe sugara, úgy a magasságkülönbségre a következő képletet kapjuk:
|
A módszer lényegét a 3.20 ábrán szemléltetjük. A Q pont P ponthoz viszonyított magasságkülönbségét megkapjuk ha az AE távolságból levonjuk az EQ távolságot. Mivel a h=AB műszermagasság valamint az l=DQ
ferde távolságot valamint a
|
Ha méréseink megkezdése előtt és azok befejezése után ismert magasságú pontról ismert magasságú pontra irányzunk, úgy a magasságkülönbség képletéből kiszámíthatjuk a mérési időszakra jellemző k értéket és megjavíthatjuk a mérési sorozatot. Ez a módszer azonban eléggé kényelmetlen, mivel a javításra csak az irodai feldolgozás folyamatában kerülhet sor, ezért kisebb pontossági igények esetén gyakran alkalmazzák azt a módszert, hogy a mérés elején meghatározott k értékét beállítják az elektronikus tachiméteren, mely ezzel az értékkel számolja a magasságokat mindaddig, míg újabb meghatározás után új k-t nem állítanak be. Az hogy milyen sűrűn történik az új értékek beállítása nagyrészt az időjárás függvénye, de még kedvező (borult) időben sem célszerű 2 óránál tovább ugyanazzal az értékkel dolgozni.
A vízszintes alappont sűrítési technológiák
A földi felmérés módszerei ismert koordinátájú alappontokhoz képest határozzák meg a részletpontok koordinátáit. A meghatározáshoz arra van szükség, hogy a részletpontok az alappontokról közvetlenül irányozhatók legyenek. Az állami alappont hálózat pontjai korlátozott sűrűségük miatt elvileg sem elégíthetik ki ezt az igényt, ezért van szükség vízszintes alappont sűrítésre. A sűrített pontokat tehát úgy kell megválasztani, hogy róluk minden részletpont irányozható legyen. Erre a feladatra a legmegfelelőbb módszer a sokszögelés.
A sokszögelés alapelve igen egyszerű,
lényegében az előző részben ismertetett direkt
művelet (első geodéziai főfeladat) többszöri ismétlésével határozza meg az
új alappontok koordinátáit.
|
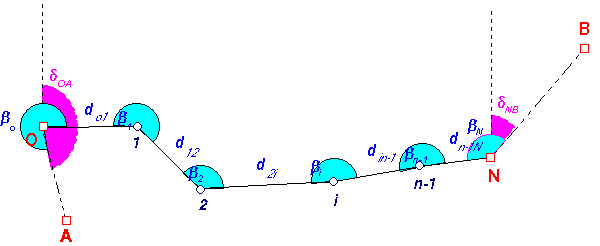
A 3.21 ábra egy sokszögvonal elvi vázlatát
ábrázolja. A, O, N, B, az állami alappont hálózat ismert koordinátájú
pontjait jelöli, 1, 2, i, N-1 pedig a sűrítés során meghatározandó új
pontokat. Mérjük meg az új pontok közötti d01, d12, d2i,
diN-1, dN-1N távolságokat és a ![]() törésszögeket a
vonal ismert kezdő és végpontján valamint a meghatározandó közbenső pontokon.
törésszögeket a
vonal ismert kezdő és végpontján valamint a meghatározandó közbenső pontokon.
Az O és B pontok ismert koordinátáiból kiszámíthatjuk a
|
|
irányszöget. Könnyű belátni, hogy az |
O1 oldal
irányszöge ![]() . Ha figyelembe vesszük,
hogy
. Ha figyelembe vesszük,
hogy ![]() , vagy általánosítva
, vagy általánosítva ![]() , úgy egymás után kiszámíthatjuk a
sokszögoldalak irányszögeit
, úgy egymás után kiszámíthatjuk a
sokszögoldalak irányszögeit
.
Ez után az irányszögek és távolságok felhasználásával a kezdőpont
koordinátáiból kiindulva sorra számíthatjuk
a sokszögpontok koordinátáit. A számítás végén azt találjuk, hogy az xN, yN koordinátákra
valamint a ![]() irányszögre két-két értékünk is van
az egyik érték a mérés feldolgozásából származik a másik pedig az eredeti
ismert koordinátákból. Ha a
megfelelő értékek különbsége (a koordináta-, illetve szögzáróhiba) nem haladja
meg az adott pontosságú sokszögelésre előírt értéket, úgy a mérésünk jó volt a
záróhibákat pedig felhasználhatjuk a koordináták kiegyenlítéssel történő
kiszámításához.
irányszögre két-két értékünk is van
az egyik érték a mérés feldolgozásából származik a másik pedig az eredeti
ismert koordinátákból. Ha a
megfelelő értékek különbsége (a koordináta-, illetve szögzáróhiba) nem haladja
meg az adott pontosságú sokszögelésre előírt értéket, úgy a mérésünk jó volt a
záróhibákat pedig felhasználhatjuk a koordináták kiegyenlítéssel történő
kiszámításához.
A sokszögelés első, talán legnagyobb szakértelmet igénylő munkafázisa a szemlélés. E munkafázisban felkeressük a meglévő alappontokat és kitűzzük az új pontok helyét. Az ismert alappontok felkeresése azért fontos, mivel igen gyakran a pontok fizikai sértetlensége nem egyezik az adattári nyilvántartással. Esetenként 30-50 %-os pontpusztulással is találkozunk. Ebből következik, hogy sokkal több alappont adatait kell kigyűjtenünk az adattárban mint ahányat a valóságban föl fogunk használni.
Ha az állami alappontok sűrűsége nagyon alacsony (2 km.-nél nagyobb távolságra vannak egymástól), rendszerint két fokozatban végezzük a sokszögelést. Az első fokozatban a sokszögpontok átlagos távolsága 600 m. a második fokozatban 150 m. Az első fokozat pontjait rendszerint kővel állandósítjuk, míg a második fokozat pontjait cövekek vagy hilti szögek jelölik.
A tulajdonképpeni mérést végző felmérő brigád
két műszakiból és két - három segédmunkásból áll. A brigád hatékony működéséhez négykerék meghajtású
terepjáró furgonra van szükség. A mérőfelszerelés
vagy rátét távmérővel ellátott teodolitból, vagy napjainkban egyre inkább,
teljes mérőállomásból áll. Az első lépésben a segédmunkások a gépkocsival
felállítanak 4-5 kényszerközpontosító műszertalppal felszerelt statívot, melyek
központosító hüvelyébe tárcsát (A pont, 1 pont) illetve műszert (O
pont) helyeznek (a 2 és 3 pontokon egyelőre nem tesznek semmit a
hüvelybe). A mérnök az O ponton megméri ![]() szöget,
és hagyományos műszer esetén a leolvasásokat bediktálja a jegyzőkönyv-vezető
segédmunkásnak, regisztráló műszer esetén pedig a műszerben tárolja. Közben a
másik műszaki vázlatot készít az álláspontról (új álláspont esetén
szalaggal beméri a különböző tereptárgyakhoz), különböző vonaltipussal
megrajzolja az észleléseket (irány, távolság, irány és távolság). Az álláspont
lemérése után az O ponton lévő hüvelybe prizmás tárcsát helyeznek majd a
gépkocsivezető segédmunkás a gépkocsival átviszi az észlelőt az 1 pontra
utána tovább hajt és prizmás tárcsát helyez a 2 ponton lévő hüvelybe. Az
észlelő megméri a d10, d12 távolságokat a
szöget,
és hagyományos műszer esetén a leolvasásokat bediktálja a jegyzőkönyv-vezető
segédmunkásnak, regisztráló műszer esetén pedig a műszerben tárolja. Közben a
másik műszaki vázlatot készít az álláspontról (új álláspont esetén
szalaggal beméri a különböző tereptárgyakhoz), különböző vonaltipussal
megrajzolja az észleléseket (irány, távolság, irány és távolság). Az álláspont
lemérése után az O ponton lévő hüvelybe prizmás tárcsát helyeznek majd a
gépkocsivezető segédmunkás a gépkocsival átviszi az észlelőt az 1 pontra
utána tovább hajt és prizmás tárcsát helyez a 2 ponton lévő hüvelybe. Az
észlelő megméri a d10, d12 távolságokat a ![]() zenitszögeket (a hosszak
redukálásához) és a
zenitszögeket (a hosszak
redukálásához) és a ![]() szöget. A jegyzőkönyvezés és
vázlatkészítés az ismertetett módon történik. A vázolt műveletsort mindaddig
ismétlik míg az N pontot is le nem észlelték.
szöget. A jegyzőkönyvezés és
vázlatkészítés az ismertetett módon történik. A vázolt műveletsort mindaddig
ismétlik míg az N pontot is le nem észlelték.
A számítást önálló sokszögvonal esetén közelítő kiegyenlítést alkalmazva zsebszámítógép segítségével már a terepen is elvégezhetjük. Ha azonban regisztrálást alkalmazunk egyszerűbb a számítást a feldolgozó programmal (pld. GEOPROFI, GEMINI) végeztetni. Sokszöghálózat esetén a számítást mindenképpen programmal végezzük.
Gyakran előfordul, hogy csak egy-két új pont
meghatározására van szükségünk (pld. a sokszögvonal kezdő,- és végpontját
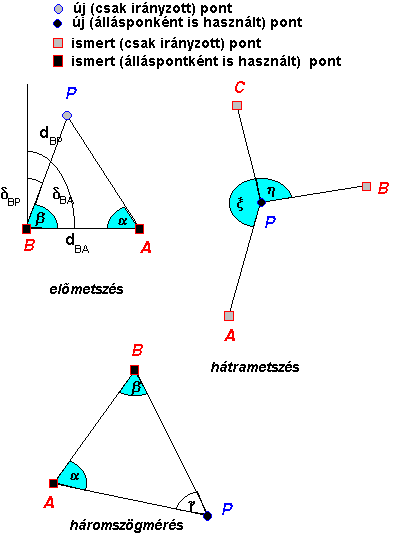
akarjuk meghatározni első lépésben), ilyenkor eredményesen alkalmazhatjuk az előmetszés,
hátrametszés vagy a háromszögmérés módszerét (3.22
ábra).
|
Az előmetszés során két ismert
koordinátájú ponton állítjuk fel a szögmérő műszert. Az A állásponton
megmérjük az AP és AB irányokat és különbségükként kiszámoljuk
az
Figyelembe véve, hogy A háromszögmérés mindössze annyiban
különbözik az előmetszéstől, hogy az új ponton is felállunk és a háromszög
mindhárom szögét megmérjük. Az elkerülhetetlen mérési hibák következtében a
három szög összege általában eltér 180 foktól, ezt az eltérést ez esetben is
záróhibának nevezzük. A záróhiba harmadával megjavítjuk az .
|
A hátrametszés során az
ismeretlen pontot használjuk álláspontnak és három ismert pontra (ezek
általában magas pontok: templomtornyok, gyárkémények stb.) irányzunk. A
mérési eredményként kapott |
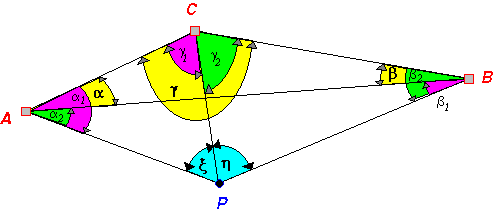
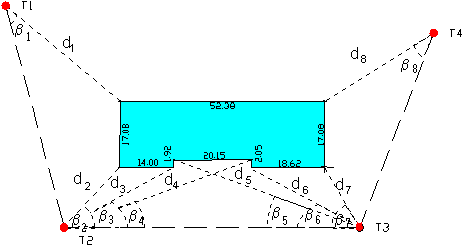
Ezért ajánlatos a hátrametszés számítását geodéziai feldolgozó program segítségével elvégezni. Arra az esetre, ha ilyen program nem áll rendelkezésre a 3.23 ábra jelöléseinek felhasználásával bemutatunk egy viszonylag egyszerű, zsebszámológép felhasználásával megoldható számítást
|
A
feladat megoldásához az A, B, C pontok ismert koordinátáiból kiszámoljuk a |
Az irányszögek ismeretében kiszámítjuk az
ismert pontokat összekötő irányok által bezárt szögeket: ![]() .
Ezek után vezessük be a következő jelöléseket:
.
Ezek után vezessük be a következő jelöléseket:
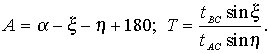
A megoldáshoz szükséges ![]() szöget ezután az
alábbi kifejezésből nyerjük:
szöget ezután az
alábbi kifejezésből nyerjük:
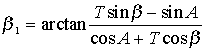 .
.
|
Most már csak arra van szükségünk, hogy kiszámítsuk a |
|
irányszöget és a |
|
távolságot. |
|
A |
|
Figyeljük |
meg, hogy ha a ![]() szög
kisebb mint 180 fok (a P pont az AB egyenes "alatt" van),
szög
kisebb mint 180 fok (a P pont az AB egyenes "alatt" van), ![]() értéke negatív.
értéke negatív.
A végeredményt, a P pont keresett
koordinátáit a direkt feladat
képleteibe való behelyettesítés után az alábbi kifejezésekből számítjuk:
![]()
![]()
Részletmérési módszerek
A tömeges helyzeti adatgyűjtést a különböző részletmérési módszerek realizálják. E módszereket többféle szempontból is csoportosíthatjuk. Ha az osztályozás alapja a fölmérés végterméke, úgy kataszteri felmérésről, mérnöki felmérésről és topográfiai felmérésről beszélünk.
A tiszta kataszteri felmérés az ingatlanok jogi határait hivatott rögzíteni. Alapkoncepciója abból indul ki, hogy a telkek folyamatosan borítják a föld felszínét. Ebben a felfogásban a felmérés tárgyai egymással határos zárt poligonok. Az elemi területekből nagyobb összefoglaló objektumok (tömbök, belterület, külterület, község, megye stb.) képezhetők. A tiszta kataszteri felmérés digitális reprezentációja nem igényel bonyolult rétegbeosztást sem, a legfőbb rétegképző elvet a telkek földhasznosítási jellege szolgáltatja. Feltehetőleg abból a gyakorlati tapasztalatból kiindulva, hogy a kizárólag jogi határokat tartalmazó térképek szinte semmire sem használhatók a legtöbb országban még ha fel is tüntetik a jogi határokat a kataszteri térképek tartalmát valós objektumokkal is bővítik. Nagy Britanniában és részben a kiterjedt volt angol gyarmatbirodalomban tilos a jogi elméleti határok rögzítése és a térkép csak az általános határokat tartalmazza (lsd. 1.3.2 ), amennyiben azok tereptárgyak (kerítések, sövények), vagy csak olyan valódi tereptárgyakat tartalmaz, melyektől számított méretek a földnyilvántartási vázlaton a telek határait meghatározzák. Magyarországon a tereptárgyak és jogi határok együttes ábrázolását az Egységes Országos Térképrendszer földmérési alaptérkép alrendszere hivatott megvalósítani.
A kataszteri térképek méretaránya függ a telkek átlagos nagyságától, és a kérdéses ország hagyományaitól. Hazánkban városokban 1:1000 (kivételesen 1:500), falvakban 1:2000, külterületen 1:4000. A kataszteri térképek általában nem tartalmaznak magasságokat. Ez alól a szabály alól kivételt képeznek a hazai 1:4000-es földmérési alaptérképek, melyekre átmásolják az 1:10 000-es topográfiai térképek domborzatát.
A mérnöki felmérések a tervezés céljaira készülnek. Az a feladatuk, hogy felhasználásukkal a műtárgyak a legjobban illeszkedjenek a terephez. Ebből következik, hogy a mérnöki felmérés során nem fordítanak figyelmet az elméleti vonalakra, hanem csak azt mérik föl ami ténylegesen a terepen található. A magassági viszonyok rögzítése különösen fontos a tervezés szempontjából. A mérnöki felmérések méretaránya a műtárgy méreteitől és jellegétől függően 1:500 és 1:2000 között változik. A térinformatika szempontjából különösen nagy jelentősége van a megvalósulási felméréseknek. Törvényi előírás, hogy amikor egy földfeletti műtárgy elkészül körvonalairól 1 m.-es talajszínt feletti magasságban, az objektum jellegének megfelelő méretarányban, felmérést kell készíteni. Fontos szabály, hogy a földalatti objektumok mindenek előtt a különböző közmű vezetékek felmérését pedig még betemetésük előtt el kell végezni. A fentiekből következik, hogy a megvalósulási felmérések tárgya mind pont-, mind vonal-, mind terület-típusú objektum lehet.
A topográfiai felmérések eredményei a méretaránytól függően vagy geodéziai térképek (1:500 - 1:1000) vagy topográfiai térképek (1:5000 - 1:100 000). Mindkét térkép típus a földfelszín mesterséges és természetes objektumait ábrázolja azzal a különbséggel, hogy míg a geodéziai térképeken minden síkrajzi objektum a térkép méretarányában kerül ábrázolásra, addig a topográfiai térképek bizonyos kis alapterületű objektumokat méretarányukon felüli egyezményes jelekkel ábrázolnak, és az áttekinthetőség érdekében ha két jel valódi helye olyan közel van egymáshoz, hogy takarnák egymást a kevésbé fontos jelet eltoltan ábrázolják.
A magasságokat a hagyományos analóg térképek általában szintvonalak segítségével ábrázolják a digitális állományok a magassági információt Digitális Magasságmodell formájában tárolják.
Míg a geodéziai térkép jellegű topográfiai felmérések lényegében azonosak a nagyméretarányú mérnöki felmérésekkel és tervezési felhasználásra készülnek addig a topográfiai térképek felhasználása sokkal változatosabb: kiterjed a honvédelem, technika, igazgatás, tudomány és kultúra számtalan területére. Egész Európára kész a legalább 1:25000 méretarányú rendszeresen felújított térképmű, hazánkban közel állunk az 1:10000-es korszerű térképmű elkészüléséhez.
A térinformatika számára a térképi méretarányok átlényegülnek felbontássá illetve helyzeti pontossággá. Ha pld. tudjuk, hogy a felmérés felbontása 1 m., akkor térinformatikai műveleteink megjelenítését nem célszerű 1:10000 -nél nagyobb méretarányban végrehajtani. Másfelől, ha a digitális állományt az 1:10000 -es topográfiai térkép szkenneléséből állítottuk elő, úgy térinformatikai műveleteink eredményeit indokolatlan 1:25000 -nél nagyobb méretarányban megjelenítenünk.
Míg a kataszteri, geodéziai térképeket, mérnöki nagyméretarányú felméréseket általában földi módszerekkel készítjük, addig a topográfiai térképeket méretaránytól függően a légi fotogrammetria vagy az ürtávérzékelés szolgáltatja. A topográfiai térképek részleges felújítására eredményesen használhatók az ürhelymeghatározó (GPS) technikák.
Visszatérve a földi módszerekre ezek osztályozását további szempontok szerint is elvégezhetjük. A térinformatika szempontjából talán a legfontosabb szempont, hogy miként történik a mérési eredmények rögzítése: kézi úton jegyzőkönyvben vagy automatikusan adattárolóban. Másik osztályozási szempont az lehet hogy milyen helymeghatározó elemeket szolgáltat a mérés. Végül fontos lehet gyakorlati szempontból, ha a módszereket az igényelt felszerelés szempontjából osztályozzuk. Az alábbiakban ismertetendő módszereknél igyekszünk figyelemmel lenni valamennyi szempontra, ezért esetenként a figyelmetlen olvasónak úgy tűnhet hogy ugyanarról a módszerről kétszer is szólunk.
Tárgyalásunk célja a térinformatikai rendszerek adatfeltöltésének vizsgálata ezért csak azokra a módszerekre leszünk figyelemmel melyek alkalmasak tömeges adatnyerésre.
Derékszögű
koordinátamérés
Ezt a módszert használták az esetek döntő többségében a múlt század második felében megindult kataszteri felmérésekben. A módszer előnye, hogy rendkívül egyszerű és olcsó felszerelést igényel, hátránya a nagy élőmunka szükséglet valamint az hogy a mérési eredmények regisztrálása hatékonyan nem automatizálható. Azt sem szabad figyelmen kívül hagynunk, hogy a módszer csak kifejezetten sík terepen használható, mivel ferde terepen a szögprizmában nem látható egyszerre a vonal két végét jelző kitűzőrúd s így a talppontkeresés nem oldható meg.
A mérőbrigád optimális összetétele: két műszaki és hat
segédmunkás. A felszerelés egy 50 m.-es mezei szalagból, két kézi szalagból
(20-50 méteres), hat kitűzőrúdból egy készlet jelzőszögből és egy kettős
szögprizmából áll.
A módszer lényegét a 3.24 ábra segítségével tekinthetjük át:
|
Első lépésként a műszakiak bejárják a terepet, kijelölik az objektumok bemérendő pontjait, erre elsősorban telekfelmérésnél van nagy szükség, amikor a telek határok töréspontjait gyakran bonyolult eljárás keretében kell a helyszínen azonosítani, felkeresik az alappontokat és megvizsgálják, hogy nincs e szükség további alappontsűrítésre a felméréshez. |
|
Szükség esetén elvégzik az alappont sűrítést, majd elkészítik a mérési jegyzet alapjául szolgáló rajzot, mely tartalmazza az alappontokat valamint a felmérendő objektumokat. Mivel az objektumokat mindig töréspontjaikkal mérjük fel lényeges, hogy minden töréspont rajta legyen a rajzon és hogy az alappontokat összekötő egyenesekről a majdani mérési vonalakról minden részletpontra a mérési vonalra merőlegesen rálátás legyen. A rajzot olyan méretarányban kell készíteni, hogy a mérési eredmények (távolságok) beírására kellő hely maradjon.
A mérés azzal kezdődik, hogy a segédmunkások kifeszítik a mezei szalagot az első alapponttól kezdődően az első és második alappont által meghatározott mérési vonalba. A szalag végeit jelzőszögekkel rögzítik, a mérési vonal végpontjaira pedig kitűzőrudakat helyeznek el. Egy - egy segédmunkás a vonal jobb illetve bal oldalán felkeresi a bemérendő pontokat. Az egyik műszaki a szögprizmával sorra megkeresi a felmérendő részletpontok talppontjait a mérési vonalon és leolvassa az abszcissza értékeket a mezei szalagon. Minden abszcisszához tartozik egy ordináta érték, melyet két-két segédmunkás mér kézi szalaggal az alapvonal jobb és bal oldalán. A jegyzetvezető technikus koordinálja a segédmunkásokat és beírja a leolvasott abszcissza és ordináta értékeket a mérési jegyzetbe. A jegyzet készítés formai szabályai megfigyelhetők a 3.24 ábrán. A töréspontok bemérése után - ellenőrzésként - bizonyos részletpontokat (pld. az épület oldalait) össze is mérnek.
A hagyományos feldolgozás során még a terepi irodában mérethelyesen felrakják az alappontokra támaszkodva a derékszögű méretek segítségével az objektumokat, ezt a munkarészt hívják mérési vázlatnak. Számítógépes feldolgozás esetén a GIS szoftverek COGO moduljai segítségével valósítják meg a pontok bevitelét és koordinátaszámítását. Az objektumok létrehozását a mérési jegyzetre támaszkodva az EDIT modulokban végzik. A mérési jegyzetre azért van szükség a szerkesztésnél is mivel ez tartalmazza az összekötési információt. Gyakran végzik a térképezést a közismert rajzi szoftverben az AUTOCAD-ban ilyenkor célszerű a bevitelt és szerkesztést külön e célra készült AUTOLISP program segítségével vezérelni.
Poláris
koordinátamérés
A módszert a következő pontban szereplő
tachimetriától csak a hagyományokon alapuló kataszteri szemlélet különbözteti
meg. Arról van ugyanis szó, hogy amint azt a 3.25 ábrán is szemléltetjük, lehetőségünk
van az objektumot határoló töréspontokat poláris rendezőikkel is meghatározni.
Elvileg tehát ha felállunk az alappontokon egy teodolittal és megmérjük a
pontokra menő irányok szögét az alapvonallal úgy megkapjuk a pontok helyzetét a
relatív rendszerben meghatározó szögeket, ha pedig egy szalaggal megmérjük a
pontok alapponttól mért távolságait is, úgy mindkét poláris rendező
rendelkezésünkre áll.
|
|||
|
A valóságban azonban ezt a módszert ebben a
formájában tömegesen szinte sohasem használták, mivel a teodolit a
szögprizmához képest mindig igen drága eszköz volt, ugyanakkor a szalaggal
történő távolságmérés gazdaságosan csak rövid távolságra végezhető. Így nem lehet kihasználni a teodolitoknak
azt az előnyét hogy ellentétben a szögprizmákkal nagy távolságra is pontos
szögértékeket szolgáltatnak (pontosabban, a szögprizmák a talppontkeresésnél
csak jelentős hibával tűzik ki a merőlegest s ez nagyobb távolságon már
jelentős lineáris eltérést ad, míg a teodolitok szögmérési hibája olyan
alacsony, hogy jelentős távolságon sem eredményez jelentős lineáris
eltérést). |
|||
A módszer azonban nagyon hatékony lehet ha a távolságokat elektronikus távmérőkkel mérjük, vagy még jobb ha műszerként teljes mérőállomást (total station-t) használunk. Igen ám, de ha így mérünk, úgy a magassági szögeket is mérnünk kell a távolságok vízszintes redukciójához. Ez pedig azt jelenti, hogy a magasságkülönbségek meghatározását is elvégezhetjük gyakorlatilag ugyanazokkal a mérési eredményekkel amelyekre a vízszintes értelmű meghatározáshoz szükségünk volt, mindössze az álláspont műszermagasságát és az irányzott pont jelmagasságát kell még pótlólagosan feljegyeznünk. Ezért ezt a módszert a tisztán vízszintes meghatározást biztosító poláris méréstől megkülönböztetendő tachimetriának hívják.
Mi nem tartjuk indokoltnak ugyanazon módszer különféle névvel illetését attól függően, hogy mérési eredményei közül mit hasznosít a feldolgozásban ezért a továbbiakban az általános módszer, a korszerű tachimetria, kissé részletesebb ismertetésére térünk át.
Elektronikus
regisztráló tahimetria
A feladatot napjainkban már szinte kizárólag teljes mérőállomás segítségével oldjuk meg. A korszerű mérőállomások 500-2500 méteres körön belül alkalmasak a felmérésre. A műszerek mind a mérési eredményeket mind a mért pontok jellegkódjait belső memória kártyán, ritkábban külső adatgyűjtőben tárolják.
A mérés előkészítése során első feladatunk a mérendő objektumok jellegkódjainak kidolgozása. A jellegkódnak alkalmasnak kell lennie arra, hogy besorolja az objektumot valamely fedvénybe, leírja az objektum típusát, megadja a típuson belüli helyét és utaljon az objektum osztályára. Például egy ásott kút esetében alkalmazhatjuk a következő kódot: vkut1oe, ahol v a fedvény (vízrajz) mutatója, kut az objektumtípus neve, 1 pld. azt jelöli, hogy a szóbanforgó kút ásott és 15-20 m. mély, oe pedig arra utal, hogy a kút önálló pontobjektum. A további feldolgozás szempontjából külön figyelmet érdemelnek azok a pontok, melyeket mind síkrajzi mind magassági értelemben figyelembe kell venni. Ezeknél a pontoknál kettős objektumkódot kell alkalmaznunk, mely lehetővé teszi, hogy a feldolgozó program most már a megfelelő kóddal mind a síkrajzi, mind a magassági állományba bemásolja e pontokat. A kialakított kódtáblázatot célszerű olyan formátumban kinyomtatni, hogy a terepen kényelmesen lehessen használni. Az előkészítés folyamán a kódokat bevisszük a műszer "verem" memóriájába ahonnan az észlelések rögzítésekor elő lehet hívni (és nem kell a terepen hosszadalmasan bebillentyűzni).
Az előkészítés másik terméke a terep bejárása során készített mérési jegyzet - alap és ha magassági felmérést is végzünk az idomváz. E rajzi termékeket célszerű régi térképek vagy légifényképek megfelelő méretarányra hozott (nagyított vagy kicsinyített) másolatain elkészíteni. A mérési jegyzet - alapon feltüntetjük az objektumok felmérendő töréspontjait és az objektum kódokat olyan méretarányban, hogy a pontok mellé sorszámaik kényelmesen elférjenek. Ha régi térképeket vagy fényképeket használunk különös figyelmet kell fordítanunk a megszűnt objektumok törlésére és az új objektumok pótlására. Az idomvázon a domborzat törésvonalait tüntetjük fel a gerincvonalakat, völgyvonalakat, lejtőátmeneti vonalakat, ezen kívül a jellemző helyeken feltüntetjük a terepen haladó vízszinteseket és a rájuk merőleges esésvonal irányokat.
Az előkészületek során megvizsgáljuk az alappont ellátottságot és szükség esetén az ismert módszerekkel új alappontokat hozunk létre. Bár elvileg meg van a lehetőség a felmérés és alappont sűrítés időbeli összekapcsolására, a gyakorlati tapasztalatok azt látszanak alátámasztani, hogy megnyugtatóbb a két mérési fázist időben különválasztani és csak akkor elkezdeni a részletes felmérést amikor az alappontok koordinátái már ismertek.
A mérőbrigád két műszakiból és két három segédmunkásból áll. A segédmunkások botra szerelt prizmákkal, rádió adó-vevőkkel és kisebb méretarányú felmérés esetén (1:4000 és kisebb) járművel (bicikli, motorbicikli, terepjáró) vannak felszerelve. Az egyik technikus kezeli a műszert, a másik vezeti a rajzokat és irányítja a segédmunkásokat.
A műszer kezelője a pontra állás után megméri a műszermagasságot, a hőmérsékletet és légnyomást, inicializálja a vízszintes és magassági köröket és elvégzi az alapbeállítást. Ezután regisztrálja az álláspont adatait és megkezdi a mérést. Mivel feltételezésünk szerint az alappontok koordinátái a felmérés megkezdése előtt már ismertek célszerű azokat még az előkészítés stádiumában bevinni az adattárolóba. Az első mérés a vízszintes kör tájékozását eredményezi. Ha a koordináták be vannak táplálva a kezelő a megfelelő billentyűk lenyomásával és a pontszámok bebillentyűzésével behívja az álláspont koordinátáját majd a tájékozó alappont koordinátáját (BS), beirányozza a tájékozó ponton elhelyezett jelet és a tájékozási függvény gombjának a lenyomásával tájékozza a vízszintes kört. Mivel a tájékozási művelet végrehajtása független a rögzítéstől célszerű a tájékozó pontot ismét megirányozni és a leolvasást rögzíteni.
Ezután kerül sor a részletes felmérésre. A vázlatvezető rádión elküldi a prizmásokat a soron következő pontokra, ahonnan megérkezésük után jelentkeznek, bemondják, hogy hol vannak és bediktálják a prizma magasságot. A műszerkezelő beirányozza a prizmát megkérdezi a vázlatvezetőtől a jelmagasságot és pontkódot, egyezteti a pont sorszámát és elvégzi a regisztrálást. Célszerű azt a regisztrálási maszkot választani mely az eredeti mérési eredményeket regisztrálja. A vázlatvezető beírja a mérési jegyzetbe vagy az idomvázba a műszerkezelővel egyeztetett pontszámot (ha a síkrajz szegényes lehetséges egyesített mérési jegyzet és idomvázlat vezetése is). A vázolt feladatokat valamennyi álláspontnak kijelölt alapponton megismétlik. Különös figyelmet kell fordítani arra, hogy ne felejtsük el minden állásponton regisztrálni az állásponti adatokat.
Az irodai feldolgozás során első lépésként a regisztrált adatokat kell bevinnünk a számítógépbe. Memória kártyára történő belső rögzítésnél ez kétféle képen is történhet: kártyaolvasó segítségével vagy a műszerbe csatlakozó kábelen keresztül. A külső adatrögzítőt ugyancsak a kábellel csatlakoztatjuk a számítógép soros portjára.
Magát az átvitelt vagy valamelyik geodéziai feldolgozó program megfelelő modulja kezdeményezi (pld. GEOPROFI) vagy a műszer szállítójától kapott programot kell előbb installálnunk a számítógépünkön és annak futtatásával érjük el az átvitelt. A geodéziai programok jelentősége abban van, hogy segítségükkel ki tudjuk számolni a pontok koordinátáit.
Ahhoz, hogy a felmérés eredményeiből digitális síkrajzi térképet állítsunk elő valamely rajzoló szoftvert kell igénybe vennünk. Számtalan ilyen szoftverrel találkozunk a piacon, de nemzetközi szempontból nézve a legelterjedtebb általános rajzoló szoftver az AUTOCAD illetve a digitális térképezéshez készített speciális rajzoló szoftver a MicroStation. A két szoftver között a térképkészítés szempontjából az a leglényegesebb különbség, hogy a térképi vonalak, szimbólumok, felirat és keretkialakítás az AUTOCAD-ben bonyolultabb programozási munkát igényel mint a MicroStation-ban. Az AUTOCAD programozási nyelve az Autolisp, míg a MicroStation az úgynevezett UCML (User CoMmand Language)(Felhasználói PaRancs Nyelv)-ben programozható. Hazánkban különösen kataszteri térképezésre előszeretettel használják az ITR térképszerkesztő programot is.
A geodéziai feldolgozó program segítségével kiszámítottuk a pontok koordinátáit és a kódok felhasználásával különválasztottuk a tisztán magassági pontokat a síkrajzi pontoktól. Ha egy részletpont mind magassági mind síkrajzi értelemben felhasználásra kerül, úgy azt mind a két pontlistába be kell másolni, de a síkrajzi listából magasságra utaló kódját, a magassági listából pedig síkrajzi kódját el kell hagyni.
A magassági adatokból némelyik geodéziai feldolgozó program (pld. a GEMINY) digitális magasságmodellt illetve szintvonalas térképet generál. Szerényebb képességű geodéziai program esetén a magassági pontfájlt valamely DEM vagy TIN modullal rendelkező GIS szoftverrel (pld. ArcInfo) esetleg a földtudományok terén igen elterjedt SURFER nevű szintvonal rajzoló programmal dolgoztatjuk fel.
A síkrajzi adatokat rendszerint a rajzoló programokban editáljuk. Ehhez mindenek előtt arra van szükség, hogy az ASCII fájlokat bevigyük a rendszerbe mégpedig olymódon, hogy a kódoknak megfelelően a pontok különböző rétegekre kerüljenek, a pontszámok (külön rétegen) a pontok mellé kerüljenek, a pontokat pedig jellegüknek megfelelő szimbólumok jelöljék. Ha a végterméken a pont jellege nem igényel külön szimbólumot akkor a szerkesztést segítendő olyan körökkel jelöljük, melyek egy külön rétegen helyezkednek el s így a szerkesztés befejezése után törölhetők.
A szerkesztést a mérési jegyzet segítségével hajtjuk végre, a lehetőség szerint maximálisan kihasználva az adott rajzi rendszerben rejlő topológiát. Azaz ha például az objektumunk zárt sokszög úgy az AUTOCAD szoftver használata esetén a 'pline' paranccsal végezzük az összekötést mivel így a későbbi formátum transzformációt sok buktatótól kímélhetjük meg.
Az elkészült térképet rajzológépen rajzoljuk ki. Ha nem célunk a papír térkép előállítása, hanem kizárólag a GIS rendszer adatfeltöltése, úgy végleges szimbólumokat, feliratokat a rajzoló rendszerben nem alkalmazunk, hanem csak az összekötéseket végezzük el és az állományt DXF formátumba transzformálva bevisszük a GIS-be.
Színtezést
alkalmazó módszerek
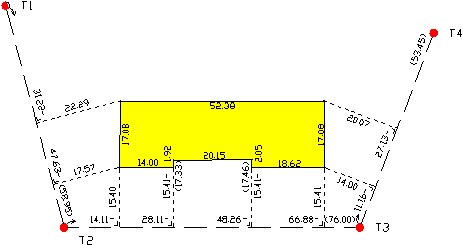
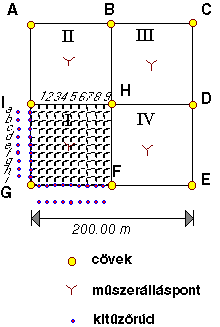
Az egyetlen többé-kevésbé teljes, főként szintező műszerrel végrehajtott részletfelmérési eljárás a négyzethálós terület szintezés. A módszer lényegét a 3.26 ábra segítségével mutatjuk be.
|
A felmérendő területet 200x200 m.-es nagy
négyzetekre osztjuk távmérő és teodolit segítségével. A nagy négyzetek
sarokpontjait 50-60 cm.-es keményfa cövekekkel jelöljük. Valamely alappont sűrítési
eljárással meghatározzuk két sarokpont koordinátáit, majd alappont szintezéssel
beszintezzük az egyik alappontot. |
|
Ezután a lécesek előre mennek a kis négyzetek következő oldaláig és a folyamat mindaddig ismétlődik míg valamennyi nagy négyzet összes kis négyzete sorra nem kerül.
Hagyományos feldolgozás esetén a lécleolvasásokat a négyzetháló rajzán rögzítik, automatikus feldolgozás esetén terepi adatrögzítő használata a célravezető. Ebben az esetben a lécleolvasás mellett rögzíteni kell a nagy négyzet sorszámát és a kis négyzetek sor és oszlop indexét is. A módszert nagy magassági pontossága miatt elsősorban öntözési-lecsapolási feladatok tervezési térképeinek előállításához használják. A módszer szélesebb elterjedését nagymértékben akadályozza, hogy gazdaságtalanabb a tahimetriánál, kevéssé alkalmas az automatizált adatrögzítésre és feldolgozásra és nem alkalmas a síkrajz szabatos rögzítésére.
A hagyományos mérnöki tervezésben általánosan használt hossz-keresztszelvény
szintezésnek nincs jelentősége a térinformatikai rendszerek helyzeti
adatokkal való feltöltésében.
- a következő részben megkezdjük a fotogrammetriai adatnyerés tárgyalását
- esetleg visszatérhet az előző részhez
- illetve a tartalomjegyzékhez
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc
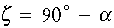


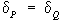 ,
,
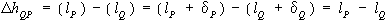


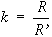
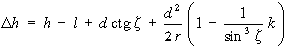 .
.
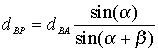
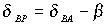 , a keresett koordináták a következő kifejezésekből nyerhetők:
, a keresett koordináták a következő kifejezésekből nyerhetők: 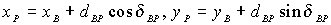 .
.