GIS műveletek II
Ebben a részben folytatjuk a GIS műveletek tárgyalását. Először
- a lekérdezések térbelivé alakításával foglalkozunk, majd rátérünk
- a szomszédság elemzés kérdésére, ezután
- a méret-meghatározó függvényeket tárgyaljuk, végül
- az összevonás, átkódolás, egybeolvasztás műveleteivel zárjuk a lapot.
A lekérdezések térbelivé alakítása
Ha szigorúan vizsgáljuk a GIS feldolgozási - elemző
műveleteit úgy arra a következtetésre juthatunk, hogy tulajdonképpen valamennyi művelet valamilyen
formában lekérdező művelet, esetleg olyan segéd művelet, mely valamely
lekérdezés végrehajtását hivatott elősegíteni.
Az, hogy az eredményeinket gyakran csak nagy számú műveletsor eredményeképpen
nyerjük az elvi és implementációs adatmodell túlzott egyszerűségével
magyarázhatjuk. Amint arról már szóltunk, ha összetett adatmodellt alkalmazunk
objektum orientált implementációban, úgy a rendszer felépítését az adatbázis
létrehozásakor kell elvégeznünk, ha az adatmodell egyszerű akkor a bonyolult struktúrák létrehozását a
GIS műveletek segítségével végezzük. A fentiekből
következik, hogy bonyolult adatmodell egyszerű lekérdezést, egyszerű adatmodell
bonyolult lekérdezést eredményez. Mivel a gyakorlatban működő rendszerek
többsége egyszerű adatmodellel dolgozik nem kerülhetjük meg, hogy a bonyolult
lekérdezés eszközeit is megismerjük.
Már itt el kell azonban mondanunk, hogy a szoftver által rendelkezésre bocsátott
eszközök többféle csoportosításban és sorrendben is aktivizálhatók
ugyanazon cél elérése érdekében. Nincs általános szabály, hogy egy
konkrét feladatot milyen utasítások milyen sorrendjével lehet optimálisan
megoldani. Ezért jelent minden újabb gyakorlati feladat komoly kihívást a
feladatot algoritmizáló GIS szakembereknek. Azt elkerülendő, hogy a tipus
feladatokat minden alkalommal újból és újból meg keljen oldani a rendszerek
jelentős része rendelkezik olyan makro nyelvvel, mely segítségével az utasítások
egymásutánjából komplex megoldó programokat lehet létrehozni. A makro nyelvek használatára egy későbbi fejezetben adunk példát.
Az egyszerű lekérdezések alapvető eszköze a korábban megismert SELECT utasítás, illetve annak különböző módosulásai. A SELECT utasítás segítségével megadva a kérdéses táblát és a keresett oszlopnevet lekérdezhetjük azokat a mezőtartalmakat, melyek kielégítik a megadott logikai feltételeket. Ezzel az utasítással lekérdezhetjük például,
- a Biztosító Társaság adatbázisából azok adatait akiknek a kérdéses biztosító területi igazgatóságán árvízbiztosítása van. Ez a lekérdezés azonban csak annyiban térbeli, amennyiben a területi igazgatóság meghatározott közigazgatási - területi egység határokon belül végzi a biztosítási tevékenységet.
Az
adott lekérdezés akkor válik térbelivé, ha a rendszer azt is le tudja
válogatni,
- hogy a biztosítottak közül kik laknak pl. árvíz veszélyes területen.
Szintén
térbelivé válik a lekérdezés, ha pld. arra vagyunk kíváncsiak, hogy
- kik azok a lakók, akik egy építendő benzinkúttól 500 m. távolságon belül laknak.
ˇ Demográfiai kutatókat érdekelheti, egy átlagosnak tekinthető tájegységben az 1 km2-re eső lakósok száma.
ˇ Hasonlóképpen térbeli a lekérdezés, ha arra vagyunk kíváncsiak, hogy milyen szerelvények találhatók egy megadott koordinátájú aknában.
A fenti kérdésekre a közönséges SQL csak akkor tudna válaszolni, ha a kérdezett jellemzők megtalálhatók volnának a táblázat valamelyik oszlopában. Bár ez például az akna koordináta vagy az ingatlan ártéri helyzete vonatkozásában elképzelhető, a másik két példában szereplő térbeli jellemzők semmiképpen sem tárolhatók attribútumként. Általános megoldásként az SQL térbeli kiterjesztése szolgál.
A térbeli kiterjesztés azt
jelenti, hogy kiegészítjük a kérdést az érdeklődésre számot tartó hely
leírásával. Míg maga az SQL többé-kevésbé szabványos a térbeli kiterjesztése
erősen szoftverfüggő. Ezért az ismertetést egy lehetséges fiktív megoldás
segítségével végezzük.
A térbeliséget a WITHIN (belül) kulcsszóval érhetjük el, melynek paraméterében megadjuk hogy a
keresést milyen idomon belül végezzük (pld. p=zárt sokszög, c=kör, w=téglalp,
t=pont b=védőövezet, n=hálózat, stb). Ezután meg kell adnunk a paraméterek
input formáját (s=képernyő, k=billentyűzet), majd az adott keresési idomhoz
tartozó paramétereket.
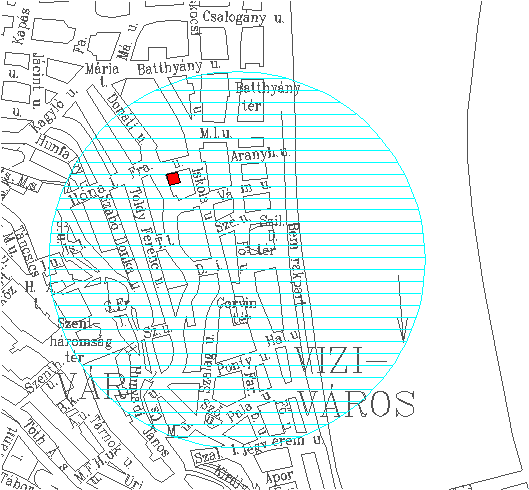
Például, ha az önkormányzat rendelkezik egy olyan táblázattal, mely tartalmazza többek közt a lakók nevét, címét, biztosítójuk nevét, biztosításuk fajtáját és arra kíváncsi, hogy a gázrobbanás 300 m.-es körzetében található lakók rendelkeznek e biztosítással pld a PROVIDENCIA biztosítónál, úgy a lekérdezést a következőképpen hajthatja végre:
SELECT NÉV, CÍM, BIZTOSÍTÁS, BIZTOSÍTÓ, JÖVEDELEMFROM NYILVÁNTARTÁS_TAB, I_KER_COVWHERE BIZTOSÍTÓ='PROVIDENCIA' AND BIZTOSÍTÁS=LAKÁSWITHIN C, CP=S, R=300;
Képzeljük el, hogy fiktív szoftverünk két képernyős üzemmódban fut, az alfanumerikus képernyőn megjelennek a bebillentyűzött utasítások míg a grafikus képernyőn az I_KER_COV azaz az első kerületet ábrázoló réteg. Ezután az alfanumerikus képernyőn megjelenő prompt azt kéri, hogy jelöljük ki a kurzorral a kör középpontját. Miután ez megtörtént a grafikus képernyőn megjelenik a keresési kör, valamint a megtalált objektumok színezett (esetleg villogó) képe (4.15 ábra), az alfanumerikus képernyőn pedig a megkívánt lista. Ha példánk esetében csak egy személy felel meg a lekérdezés kritériumainak, úgy pld. a következő listát kaphatjuk:
SOVÁNY ELEONÓRA, FRANKLIN_3, TO3, PROVIDENCIA, 32000;
ahol T03 a kérdéses lakásbiztosítás kódja.
|
|
4.15 ábra - térbeli keresés a grafikus képernyőn |
Szomszédság (régió) elemző függvények
Bár elvileg a lekérdező nyelv térbeli kiterjesztése a relációs algebra illetve a logikai műveletek segítségével tetszőleges lekérdezéseket tesz lehetővé, a gyakorlati rendszerek csak fokozatosan jutnak el az általánosításnak erre a szintjére. Ezzel magyarázható, hogy a térinformatikai tankönyvekben gyakran külön függvény csoportként emlegetik a az u.n szomszédsági (neighbourhood) függvényeket.
A szomszédsági vizsgálatoknak tulajdonképpen két összetevője van:
- a figyelembe veendő környezet határvonalainak kijelölése;
- a kijelölt környezeten belüli műveletek.
Ami magának a környezetnek a kijelölését illeti a gyakorlati
rendszerek több vagy kevesebb opciót engednek meg az előzőekben felsorolt
lehetőségek (ablak, poligon stb.) közül.
Tartalmi oldalról viszont annak van különös jelentősége, hogy milyen
alapon határozzuk meg a régiót.
- Ha valamely ponttól való távolság alapján végezzük a vizsgálatokat (mint a fenti példánkban), úgy egy kör metszi ki a kérdéses rétegből a megvizsgálandó objektumokat.
- Ha vonalas tereptárgyaktól konstans távolságon belül fekvő objektumokat keresünk, úgy a figyelembe veendő terület határait a tereptárggyal párhuzamos vonalak illetve körívek fogják határolni.
- Hasonló a helyzet ha a keresett objektumok valamely terület határaitól adott távolságon belül helyezkednek el.
Ezek a keresési tartományok mindhárom esetben nagyon hasonlítanak a védőövezetnek (buffer zone) nevezett, program által konstruált, későbbiekben még ismertetendő objektumokra azzal az elvi különbséggel, hogy a keresési tartományok ideiglenes képződmények míg a védőövezetek végleges objektumok.
Ha a szoftver nem teszi lehetővé ideiglenes keresési tartományok alkalmazását, úgy a feladatot, kissé körülményesebben, védőövezet generálással oldhatjuk meg.
Gyakori az az eset, amikor a szomszédságot valamely
adminisztratív egység (választókörzet, kerület, megye, stb.) határa definiálja.
Ebben az esetben a rétegekkel dolgozó implementációs modellek a síkba feszítés
élvének megfelelően külön rétegen tárolják az adminisztratív határokat és külön
rétegeken a telkeket, épületeket, földhasználatot, stb. Kézenfekvő, hogy ebben
az esetben nem volna gazdaságos a határok ismételt bevitele az ideiglenes
keresési zónák létrehozása érdekében, ezért a rendszerek többsége ilyenkor a
fedvényezési (overlay) eljárás valamely módozatát alkalmazza a vizsgálandó
terület létrehozására. Mivel a
fedvényezés a GIS főművelete erről a továbbiakban még
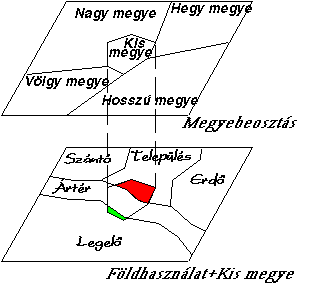
részletesen szólunk, jelen témánkhoz a 4.16 ábra segítségével csak egy speciális válfaját a pogácsa
szaggató (cookie-cutter) módszert mutatjuk be.
|
Két fedvényt használunk a művelet bemutatására. Az első fedvényen a megyék beosztása a másodikon a földhasználat került ábrázolásra.
|
|
A művelet eredményeképpen az új rétegen (kényelmi szempontból a változatlanul maradt eredeti földhasználati réteget nem tüntettük fel) megkaptuk azokat az új objektumokat, melyek Kis megyéhez tartoznak és legelő, ártér illetve település földhasználati osztályba tartoznak.
Az ezekhez az új objektumokhoz tarozó területek értékei a művelet hatására automatikusan kiszámítódnak az attribútum táblázatban és kívánságra listázhatók. A vázolt művelet annyiban tér el a szabványos fedvényezési eljárástól, hogy nem teljes fedvények között hajtódik végre, hanem az egyik fedvényen csak egy kiválasztott objektumot vonunk be a műveletbe.
Tartalmi oldalról az volna az optimális, ha a szoftver a felhasználó által megfogalmazott képletbe foglalva tetszőleges műveletek végrehajtását lehetővé tenné a szomszédság határain belül lévő attribútumokkal. Bár több újabb rendszer már alkalmas általános felhasználói képletek fogadására a hagyományos szoftverek általában a következő beépített, szomszédsági statisztikai függvényekkel rendelkeztek:
- átlag képzés - a kiválasztott attribútum érték számtani közepét számolja a szomszédságba eső objektumokból;
ˇ különbözőségi mérték képzése - kiszámolja a kérdéses attribútum érték szórásnégyzetét (varianciáját) a kérdéses területre;
ˇ gyakoriság számítása - a 3.50 ábrán bemutatott egydimenziós hisztogram számítása, a legnagyobb ordinátához tartozó attribútum érték listázása;
ˇ szélső értékek megkeresése - a legnagyobb vagy legkisebb attribútum érték kiválasztása és listázása;
ˇ összeg képzés - az attribútum összegének számítása, gyakran az összeget elosztják a szomszédság területével, pld. ha a kérdéses attribútum a lakásonkénti lakók száma, úgy e függvénnyel meghatározható az összlakosság illetve a népsűrűség.
Méret-meghatározó függvények
A 2. fejezetben már viszonylag részletesen foglalkoztunk a metrikus jellemzők meghatározásaival és számítási algoritmusaival vektoros és raszteres adatmodell esetén. Jelen pontban csak a teljesség kedvéért foglaljuk össze a metrikára vonatkozó ismereteinket.
Talán a legfontosabb méret a távolság. Amint
láttuk a GIS nem csak az euklidesi távolságot használja, hanem a Manhattan
távolságot is. Ez utóbbi használata különösen hálózati feladatok
megoldásában indokolt. A távolság a mellett, hogy önállóan is lekérdezhető,
több más összetett GIS függvénynek is alkotó eleme.
Példaként említhetjük az előző pontban tárgyalt vizsgálati terület kijelölést,
a védőövezet generálást vagy a hálózatokkal kapcsolatban ismertetendő optimális
útvonal tervezést, elosztást és hozzárendelést, stb.
A vonalas objektumok hosszát,
a területi objektumok területét és kerületét a vektoros rendszerek a topológia
létrehozásakor automatikusan számolják és elhelyezik az objektum attribútum
táblájában. Ezeknek a mennyiségeknek a listázása
illetve a felhasználása különböző műveletekben még az előtt eszközölhető
mielőtt a geometriát összekapcsoljuk a tulajdonságjellemző adatokkal.
A raszteres rendszerek esetén az attribútumok
kezelése s így a metrika alkalmazási feltételei is erősen függnek a szoftver
korszerűségétől. A korai vagy inkább primitív raszteres rendszerek ugyanis
általában nem kezelnek attributív adatbázist. Az egyes rétegeken található
objektumok pixelenként osztályba sorolásuknak megfelelő kóddal vannak ellátva,
melyek rendszerint egész számok. A kódként alkalmazható számtartomány nagyságát
az határozza meg, hogy a kérdéses adatmodell hány bitet tartalékol a kód
számára. A tulajdonságjellemző kódok értelmezését (jelmagyarázatát) rendszerint
a raszteres kép fejezetében helyezik el. Ilyen rendszerekben csak többszöri átkódolás és
munka-fedvények sorozata segítségével végezhetők el a különböző műveletek, így
a metrikus műveletek is.
A korszerű raszteres rendszerek esetében ilyen problémák nem lépnek fel, mivel ezek a rendszerek pixel
azonosítóként objektum azonosítót alkalmaznak, mely kapcsolatot teremt a pixel
csoport és az attribútum tábla között. Ugyanakkor a
raszteres modell lényegéből fakadó előnyök és hátrányok változatlanul maradnak,
ami esetünkben azt jelenti, hogy a területek és távolságok számítása egyszerű, míg a kerület
számítás viszonylag bonyolult és kevésbé pontos.
Tulajdonság összevonás, átkódolás, egybeolvasztás
Az előző pontban említettük, hogy az egyszerű raszteres
rendszerek gyakran egy-egy számmal jellemzik az egyes pixelek tulajdonságait.
Gyakran előfordul, hogy olyan vektoros állományoknál, melyek gazdag attribútum
táblával rendelkeznek mesterségesen hozunk létre olyan helyzetet, hogy az objektumokat
csak egy-egy szimbolikus leíró adat jellemezze. Ezek az 'új' adatállományok általában
ideiglenes képződmények és csak addig léteznek, amíg az elemzés eredményét nem
publikáljuk. Az eredeti adatállományok a műveletek során nem sérülnek (az
átalakított adatállományokat új névvel láttuk el) és más feladatokban más
jellemzőjük alapján végezhetjük a módosítást.
|
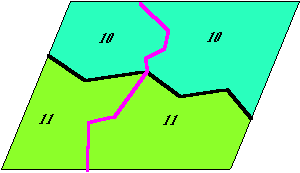
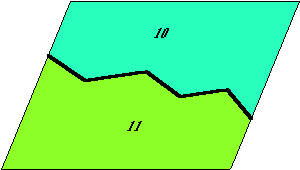
A 4.17 ábra
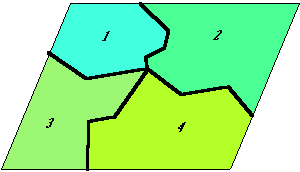
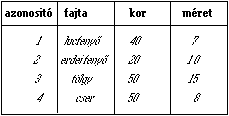
csoporton egy nagyon egyszerű példán illusztráljuk a tulajdonság összevonást,
átkódolást és egybeolvasztást. Az erdészeti rétegen négy különböző
tulajdonság jellemzőkkel rendelkező objektum szerepel. Feladatunk, hogy
meghatározzuk a tűlevelű erdők területét. Mivel feladatunk szempontjából nem
érdekes, hogy melyik tűlevelű fajta, milyen egyéb jellemzőkkel leírt egyedei
alkotják a tűlevelű erdőt, összevonjuk az 1 és 2 objektumot egy 10 sorszámú
objektummá, hasonlóképpen a 3 és 4 nem tűlevelű objektumokat egy 11
objektummá. Az összeolvasztás első
lépésében kialakul az új attribútum tábla egyelőre még a korábbi elválasztó vonal
megtartásával, majd a következő lépésben az azonos attribútumú objektumok
közötti határ megszűnik és a leíró tábla kiegészül (ezt az ábrán helyhiány
miatt nem tüntettük fel) az új objektumok területével és kerületével. Ha még további feladatokat
is meg akarunk oldani az összevont objektumokkal úgy sor kerülhet az
átkódolás műveletére. A legegyszerűbb esetben annak vagy azoknak az
objektumoknak, melyek a további vizsgálatból még nem estek ki 1-es
tulajdonság kódot adunk, míg a már kiesetteknek 0-ást. Az átkódolási eljárás természetesen nem csak 'bináris' kódokat alkalmazhat, lehetőségünk van a feladat szempontjából alkalmassági sorrendet felállítani a vizsgált objektumok között és tulajdonság kódként az alkalmassággal arányos egész számokat alkalmazni (egész súlyokat általában csak a raszteres rendszerek igényelnek). |
Ha például a 4.17 ábrán látható fedvényt a fakitermelés megtervezésére kívánjuk
felhasználni és a kitermelésre való alkalmasság egyik kritériumaként a fák
magasságát tekintjük (pld 10 m. alatt kitermelésre alkalmatlan, fölötte pedig
az alkalmasság arányos a magassággal), úgy olyan ideiglenes réteget hozhatunk
létre, mely három objektumból áll: a régi 3. objektum alkalmassági kódja 3, a
régi 2. objektum alkalmassági kódja 2, és a régi 1. és 4 objektumból összevont
új objektum 0 alkalmassági kóddal.
ˇ a következő részben folytatjuk a GIS elemző műveletek tárgyalását
ˇ esetleg visszatérhet az előző részhez
ˇ illetve a tartalomjegyzékhez
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc