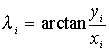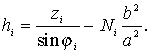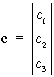TÉRBELI ADATOK GYŰJTÉSE

A térinformatikai rendszerek talán legfeltűnőbb sajátossága az adatgyűjtésben van. Mivel e rendszerekben minden tulajdonságjellemző adat helyhez kötött, a kérdéses tulajdonság-értéken kívül az adat helyét is meg kell határozni.

Azok a módszerek, melyekkel a gyakorlatilag végtelen sok fajta tulajdonságjellemzőről információt szerzünk maguk is számtalanok s ezért nem vállalkozhatunk egy fejezet keretein belül e módszerek bármennyire is rövidre fogott rendszeres ismertetésére. Megelégszünk azzal, hogy esetenként utalunk a módszereket tárgyaló tudományágra illetve példaként azokra a digitális adatállományokra, melyek egy-egy tulajdonságjellemző vonatkozásában a felhasználó rendelkezésére állnak.

Bizonyos fokig másként kezeljük a távérzékelés minőségérték meghatározó eljárásait, bár a kényszerű rövidség miatt itt sem vállalhatjuk a rendszerezett tárgyalást, helyette az osztályozási eljárások viszonylag bővebb tárgyalásával kivánjuk csak felvillantani az e módszerben rejlő lehetőségeket.

A térinformatikai adatbázisok alapvetően térbeliségükben különböznek a hagyományos alfanumerikus adatbázisoktól. Ezért az adatgyűjtés tárgyalásakor is a térbeli helyzet meghatározására fordítjuk a fő hangsúlyt. Tárgyalásunkat a referencia rendszerek megismerésével kezdjük, majd röviden összefoglaljuk az alappontmeghatározások témakörét ismertetve a hagyományos módszerek a légi- és az ürtechnikák legfontosabb vonásait. Mivel azonban a különböző technikák elvi alapjai függetlenek a felhasználás céljától, a fölösleges ismétlések elkerülése érdekében az alappontsűrítési felhasználást is a módszer általános ismertetéséhez kapcsoljuk. A tulajdonképpeni tömeges adatnyerést a részletfelmérések szolgálják legyenek azok hagyományos földi vagy fotogrammetriai eljárások, távérzékelő műholdas módszerek vagy műholdas helymeghatározó technikák.

A térinformatika megjelenésekor a felmérési tudományok már olyan fejlettségi fokon voltak, mely lehetővé tette jelentős területek kölönböző méretarányokban és különböző tartalommal történő térképezését ezért érthető, hogy e meglévő analóg térbeli adatbázisok digitalizálása még ma is jelentős forrása a térbeli adatnyerésnek. Ugyanakkor a sorrendiséggel is ki szeretnénk fejezni, hogy ellentétben a laikusok körében makacsul élő tévhittel a térképek digitalizálása nem hogy nem kizárólagos de még csak nem is elsőrendű forrása a digitális térbeli adatoknak.

A fejezetet az attributiv adatállomány létrehozásával kapcsolatos lehetőségek és problémák felvázolásával fejezzük be.

E rövid bevezető után rátérhetünk első témánkra.

Referencia rendszerek

E témakörön belül megismerkedünk a

1. globális referencia rendszerekkel, ezen belül
1. néhány geodéziai dátummal,
2. a dátumok közti transzformáció matematikai modellével és
3. magyarországi alkalmazásával,
2. a lokális referenciarendszerek fogalmával és hazai realizálásukkal, végül
3. a vetületi síkon végezhető műveletekkel .

Globális referencia rendszerek

A pont helyzetének meghatározása azt jelenti, hogy megadjuk koordinátáit valamely alapul választott vonatkozási (koordináta) rendszerben. Földi pontok esetén célszerű a vonatkozási rendszert úgy hozzákapcsolni a Földhöz, hogy helyzetét a Föld fizikai tulajdonságai meghatározzák.

3.1 ábra - Földhöz kapcsolt derékszögű koordináta rendszer

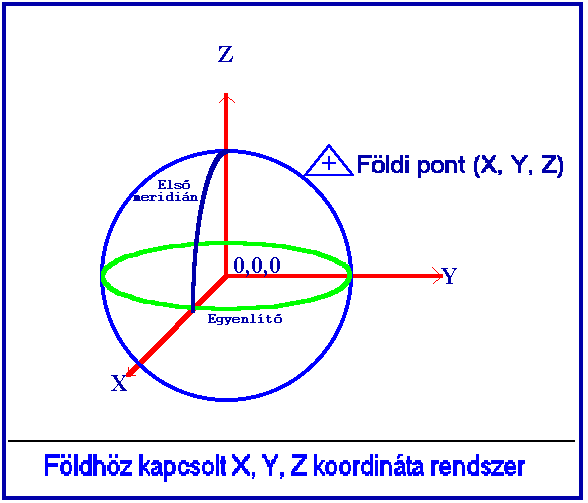
Legegyszerűbbnek az a megoldás tűnik, hogy felveszünk egy olyan X Y Z derékszögű koordináta rendszert, melynek O kezdőpontja egybeesik a Föld tömegközéppontjával, Z tengelye a Föld közepes forgástengelyével, az XZ tengelyek által alkotott sík pedig átmegy egy rögzített földi ponton (rendszerint a greenwich-i csillagvizsgáló rögzített pontján) (3.1 ábra).

Bár napjainkban a derékszögű koordináták használata a mesterséges holdak segítségével működő helymeghatározó rendszerekkel kapcsolatban egyre nagyobb jelentőségre tesz szert, a korábbi időkben a derékszögű koordináta rendszer nem volt igazán népszerű többek között azért, mert nem tudta a gyakorlati szemléletnek megfelelően szolgáltatni a magasságokat. A derékszögű rendszerben ugyanis az azonos magasságú pontok Z koordinátái különbözőek. Hogy a magasságokkal kapcsolatos igény is legalább közelítőleg kielégítésre kerüljön, a geocentrikus derékszögű koordinátarendszerre egy forgási ellipszoidot illesztettek olymódon, hogy meridián ellipszisének középpontja essen egybe az O ponttal, forgástengelye pedig a Z tengellyel. Az a és b féltengelyeket úgy választották meg, hogy a forgási ellipszoid a lehető legjobban közelítse a Föld generalizált felszínét.

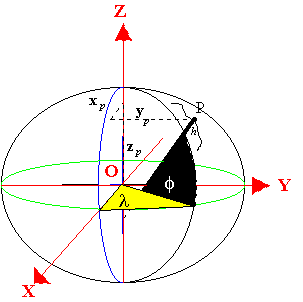
Az ellipszoidi rendszerben bármely földi pont helyzetét a következő három koordináta határozza meg: , és h. A szög a földi pont földrajzi szélessége, a szög pedig a pont földrajzi hosszúsága, míg a h távolság a pont ellipszoid feletti magassága. A 3.2 ábra tanulsága szerint a szélesség az ellipszoid pontbeli normálisának szöge az egyenlítő síkjával, a hosszúság pedig az XZ sík lapszöge a pont meridián síkjával. A geocentrikus elhelyezkedésű forgási ellipszoid féltengelyeinek (a, b) ismeretében a pont derékszögű koordinátai és földrajzi koordinátái egymásba kölcsönösen átszámíthatók.

3.2 ábra - földi ellipszoidi és derékszögű koordináta rendszerek

Jelölje Ni a Pi terepi pontból az ellipszoidra bocsátott normális döféspontjának harántgörbületi sugarát, legyen

a numerikus excentricitás.

Geometriai összefüggésekből levezethető, hogy

, és a Pi pont derékszögű koordinátái a földrajzi koordináták ismeretében az

alábbi kifejezésekből nyerhetők:

A derékszögű koordináták ismeretében _i az alábbi negyedfokú egyenletből számítható:

ahol . A hosszúságot a bemutatott kifejezések segítségével az alábbiak szerint fejezhetjuk ki:

. Végül az ellipszoid feletti

magasságot is kifejezve

A gyakorlatban használatosabb megoldást _i -re és h_i-re iterációval számítják a következő képletekből:

3.3 ábra - a geoid és ellipszoid helyzete egy P pont környezetében	3.4 ábra - a geoid és ellipszoid eltérések globális térképe

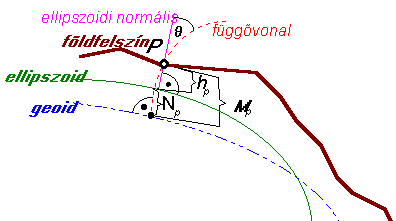
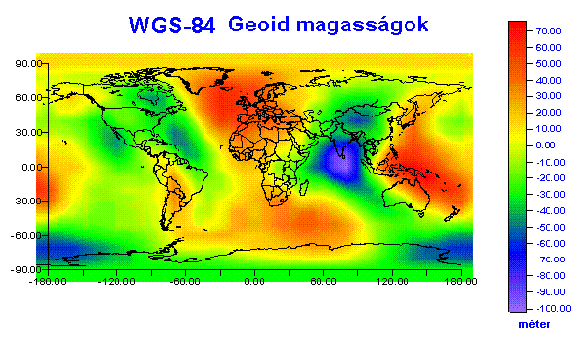
Ha abból a gyakorlati igényből indulunk ki, hogy azonos magasságú pontok között a homogén folyadék ne áramoljon, akkor magassági referencia felületként nem választhatjuk az ellipszoidot, mivel felülete, ha kis mértékben is, eltér az equipotenciális felülettől. Az equipotenciális felület olyan felület, mely minden pontjában merőleges a nehézségi erő irányára, következésképpen a rajta mozgó tömeg nem végez munkát a nehézségi erővel szemben.

Ha a nyugalomban lévő, homogén, kiterjedésében nem gátolt tengervíz szintjét képzeletben meghosszabbítjuk a kontinensek alatt úgy a nyert felületet geoidnak nevezzük. A geoid equipotenciális felület és alkalmas arra, hogy a magasságmérések referencia felületeként szolgáljon.

Amint már említettük az ellipszoid felszíne általában eltér a geoidtól. A 3.3 ábra felvázolja a geoid és az ellipszoid kölcsönös helyzetét a P pont környezetében, a 3.4 ábra pedig az ellipszoid és a geoid globális eltéréseit mutatja be színfokozatos ábrázolással.

Az ábra tanulsága szerint a P terepi pont magasságát megkapjuk, ha kivonjuk az ellipszoid fölötti magasságból (h_P) és az ellipszoid és a geoid távolságát az úgy nevezett geoidundulációt (N_P) (megjegyezzük, hogy N előjeles mennyiség, akkor pozitív, ha az ellipszoid a geoid alatt van, a 3.3 ábrán rajzolt érték tehát negatív), azaz:

M_P = h_P - N_P

.

Bár h_P az ellipszoidra bocsátott normálison tehát egy egyenesen helyezkedik el, a magasság pedig a térgörbe alakú függővonalon, a pont és az ellipszoid távolsága a normálison illetve a függővonalon mérve gyakorlatilag megegyezik s ezért a magasság kifejezésében az utóbbít joggal helyettesíthetjük h_P értékével. Érdemes megjegyezni, hogy az ellipszoid és a geoid közelségét nem csak a geoidunduláció, hanem az ábrán -val jelölt függővonal elhajlás értéke is befolyásolja. Ez utóbbi nem más mint a P pont ellipszoidi normálisának a szöge a ponton átmenő függővonal pontbeli érintőjével.

Az adott országban (vagy mérő rendszerben lsd. GPS) használt koordináta rendszert geodéziai dátumnak nevezik. Ilyen dátumok például Északamerikában a NAD27, NAD83, a GPS rendszer által használt az USA Katonai Térképészeti Ügynöksége által kifejlesztett WGS-84, az Európában kialakítás alatt álló EUREF, de tulajdonképpen dátum alapja van a hazai Egységes Országos Vetületi Rendszernek is az úgy nevezett HD-72. Általában több száz helyi dátum létezik.

A dátum állandósított földi pontok koordinátáinak meghatározásával rögzíti a koordináta rendszert a Föld testében. Elvileg a pontok derékszögű koordinátái egyértelműen meghatározzák a dátumot, ezekre a koordinátákra bármelyik forgási ellipszoid illeszthető. A WGS-84 rendszer ilyen korszerűen értelmezett dátum. Mégis, hasonlóan a korábbi dátumokhoz, valószínűleg a katonai térképezés egységes rendszere érdekében, e dátumhoz is rendeltek egy WGS-84 nevű ellipszoidot, melynek nagy féltengelye a=6 378 137 m., kis féltengelye pedig b=6 356 752.314m. A két féltengelyből számítható a lapultság is: f=1/298.2572221.

A korábbi dátumok több itt nem részletezendő okból kifolyólag (lsd. [1], [2]) csak a vízszintes helymeghatározások igényeihez alkalmazkodva egybemosták a derékszögű koordináta rendszert a rá illesztett ellipszoidot illetve (pld. az EOV esetében) az alkalmazott síkvetületet a tulajdonképpeni lokális referencia rendszert. Ez a helyzet mind addig nem okoz problémát míg különválasztva kezeljük a vízszintes és magassági pontmeghatározást, illetve nem akarunk különböző dátumokra alapozott térbeli adatokat együttesen kezelni, vagy térbeli adataink meghatározásánál nem akarjuk igénybe venni a GPS korszerű módszereit. Hogy egyszerűbben elképzelhessük a dátum fogalmát lássuk milyen adatokkal adható meg egy hagyományos, ellipszoidon nyugvó dátum, a hazai HD-72.

1. Kiválasztanak egy forgási ellipszoidot, ez esetünkben az IUGG GRS 1967, melynek tengelyei:
• a= 6378160 m és
• b=6356774.516 m.
2. Meghatároznak egy kezdőpontot, és megadják a kezdőpont ellipszoidi koordinátáit valamint ellipszoidi azimútját egy másik ismert pontra. Esetünkben ezek az értékek a következők:
• név: Szőlőhegy;

koordináták:

;

azimut az Erdőhegy nevű pontra:

.

3. Megadják a függővonalelhajlás komponenseit, vagy ezek helyett a pont csillagászati (geoidi) koordinátáit és azimutját az ismert pontra és a geoidundulációt:

csillagászati koordináták:

;

csillagászati azimut Erdőhegyre:

.

4. A fent megadott képletek segítségével kiszámíthatjuk a kezdőpont derékszögű koordinátáit és tengerszínt feletti magasságát és kiegészítő információként hozzáfűzhetjük a dátum leírásához:
• a kezdőpont derékszögű koordinátái: X=4082838.04 m, Y=1454055.97 m, Z=4664062.68 m;

a geoid feletti magasság és tengerszínt feletti magasság:

MSzőlőhegy = h – N = 235.80 – 6.56 = 229.24 m

Különválasztott vízszintes és magassági referencia rendszer esetén azonban szükségünk van magassági dátumra is. A magassági dátum nem más mint a kérdéses régióhoz közeli közép tengerszintet rögzítő stabilan állandósított magassági pont.

Ha szükségünk van a különböző vízszintes illetve három dimenziós dátumokban meghatározott pontok együttes kezelésére, illetve a GPS segítségével kívánunk meghatározni más dátumhoz kötött koordinátákat, ugy térbeli hasonlósági koordináta transzformációt kell végrehajtanunk. A geodéziai gyakorlatban gyakran alkalmazzuk a síkbeli transzformációkat, köztük a Helmert féle hasonlósági transzformáció 2 D-s válfaját is. Sajnos a transzformáció háromdimenziós variánsa egy kissé bonyolultabb, ugyanakkor széleskörűen használt a térbeli adatnyerésben, mind a globális referencia rendszerek közötti átszámításokban elsősorban a GPS módszerek használata esetén, mind a később ismertetendő fotogrammetriai adatnyerésben illetve Mobil Térképező Rendszerekben. Mivel a tényleges transzformáció számítását mindig előregyártott számítógépi programok segítségével végezzük helyszűke miatt nem megyünk bele a megoldás részleteibe, csak annak alapelvét ismertetjük.

3.5 ábra - transzformáció két térbeli (3D-s) derékszögű koordináta rendszer között A forgatási mátrixok elemeit megkapjuk ha skalárisan összeszorozzuk az eredeti tengely egységvektorát az elforgatott tengelyével ami nem más mint a két kérdéses tengely egymással bezárt szögének koszinusza. Ha ei az i sorszámú eredeti tengely egységvektora,e'k pedig a k sorszámú elforgatott tengelyé, úgy

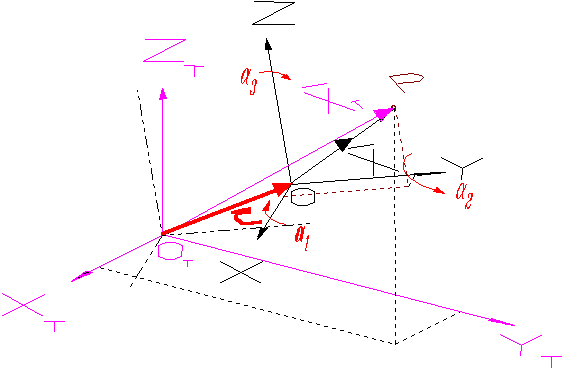
Tekintsük az X és XT vektorokat alkotó két derékszögű koordináta hármast a 3.3 ábrán (az egyértelműség kedvéért a rajzon a vektorokat felülvonással jelöltük). A két rendszer hasonlósági transzformációját az alábbi kifejezéssel határozzuk meg: , ahol µ méretarány tényező, c az eltolás vektor, azaz az R forgatási mátrix pedig a három egymást követő forgatás mátrixaiból épül fel az alábbiak szerint: .

Ha elvégezzük a tengelyenkénti forgatási mátrixok összeszorzását, úgy a forgatási mátrix a 3.3 ábra jelölései szerint a következő alakot nyeri:

.

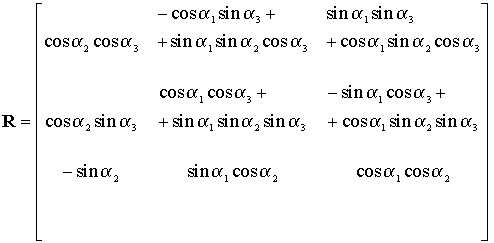A forgatási mátrix ortogonális tulajdonságokkal rendelkezik (lsd. pld [5]), ami többek közt azt jelenti, hogy három eleme ismeretében a többi hat kiszámítható.

A transzformációs feladat kétféleképpen jelentkezhet: az egyszerűbb és ritkább esetben ismerjük a transzformációs paramétereket, az általánosabb esetben viszont ez utóbbiakat is meg kell határozni.

Az első esetben, ha tehát ismeretesek a pontok index nélküli koordinátái valamint a transzformációs paraméterek, úgy a transzformációs vektor egyenlet felhasználásával ugyanezen pontok indexes koordinátái egyszerűen kiszámíthatóak. Bonyolultabb a helyzet, ha a transzformációs paraméterek ismeretlenek. Ez utóbbiak 7 ismeretlent jelentenek tehát legalább 7 közös koordinátával kell rendelkeznünk a megoldáshoz. A gyakorlatban több közös adatot alkalmaznak (legalább 3 közös pontot ami 9 közös adatnak felel meg) és a feladatot kiegyenlítéssel oldják meg (lsd. részletesebben [3]).

A megoldás fő problémája az, hogy az ismeretlenek a forgatási mátrixban nem lineáris formában szerepelnek ezért a megoldáshoz linearizálni kell az egyenletrendszert. A linearizálás ugyanakkor feltételezi az ismeretlenek közelítő ismeretét. Ha ezeket az értékeket rosszul választjuk meg úgy szerencsés esetben is csak több iteráció után kapunk megbízható megoldást. Nem térünk ki részletesen a közelítő értékek meghatározására (az érdeklődők [5]-ből megfelelő eligazítást nyerhetnek) csak utalunk rá, hogy gyakran kielégítő ha a méretarány tényező kezdő közelítő értékét egynek, az eltolási és forgatási paraméterekét pedig zérusnak választjuk.

Jelöljük az ismeretlenek közelítő értékeit (c), (µ), (R) - vel ugy a kiegyenlített értékeket a c=(c)+dc, µ=(µ)[1+dµ], R=dR(R) kifejezések szolgáltatják. A linearizált rendszerben tehát az ismeretlenek a dµ méretarány javítás, az eltolás vektor három növekménye dc^T=[dc₁ dc₂ dc₃] és a dR differenciális forgatási mátrixban elhelyezkedő forgatási szögnövekmények az alábbiak szerint:

.

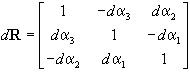A differenciális forgatási mátrixot annak a feltételezésével vezettük le az eredeti forgatási mátrixból, hogy közelítéseink igen jók és ezért

és

.

Egyetlen pont transzformált koordinátáinak linearizált modellje ezek után a következő alakban írható fel:

X_Ti=(X_T)_i+A_idp,

(13) ahol az (X_T)_i=( µ)(R)X_i+(c) kifejezés a közelítő transzformációs paraméterekből és az adott X_i eredeti koordinátákból számolható. Az A_i alakmátrix és a dp paraméter vektor a következő alakban írható fel

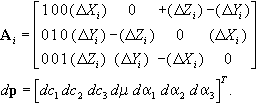
A

,

és

jelölések a transzformált közelítő koordináták és eltolás vektor komponensek különbségeiként számíthatók az alábbiak szerint:

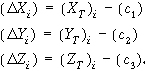
Tetszőleges n számú közös pont esetén az alakmátrix a következő alakú lesz: A^T=[A₁ A₂ ... A_n]. Abban a gyakorlati esetben amikor 3 közös pont felhasználásával kívánjuk elvégezni a transzformációt az alakmátrix a következő alakot veszi fel:

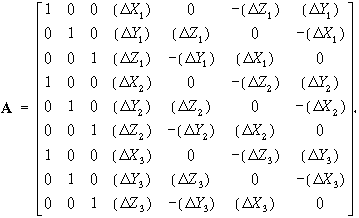
A kapott rendszer enyhén túlhatározott (két fölös adattal rendelkezünk), megoldását a legkisebb négyzetek módszere segítségével számítjuk. A részletek elhagyásával, feltételezve, hogy a mindkét rendszerben ismert koordináták pontossága azonos, az ismeretlen paraméterek növekmény vektorát az alábbi kifejezésből nyerjük:

,

ahol az l tisztatag vektor az előzetes értékekből számolható és a tényleges transzformált koordináták különbsége, azaz:

Az ismeretlen paraméterek meghatározása után felhasználásukkal tetszés szerinti mennyiségű pont koordinátáit számíthatjuk át az egyik rendszerből (pld. a WGS-84-böl) a másik rendszerbe (pld. az EOV rendszer alapját képező derékszögű térbeli koordináta rendszerbe). Meg kell azonban jegyeznünk, hogy ha a közös pontok a globális méretekhez képest túl közel vannak egymáshoz ( ez a helyzet gyakori a hazánkhoz hasonló kis országok esetében), úgy a megoldás pontossága alacsony lesz és érvényessége viszonylag szűk régióra korlátozódik. Még kellemetlenebb következménye a viszonylag közeli pontoknak, hogy kevés fölös adat esetén az egyenletrendszer együttható mátrixának rossz a kondicionáltsága, ami nem megfelelő invertáló rutin használata esetén gyakran eredményezi a rendszer megoldhatatlanságát (a kerekítési hibák következtében a rendszer "elszáll").

Ha tömören meg akarjuk fogalmazni a globális referencia rendszer szerepét a térbeli adatok kezelésében, úgy azt mondhatjuk, hogy az infrastruktúra egy meghatározott szintjét meghaladva, hagyományos, egy országon belüli adatnyerés esetén elvileg a globális referencia rendszerrel nem sok dolgunk van, ha azonban GPS-t használunk a koordináták meghatározására, úgy az ismertetett transzformációk alkalmazása nélkül nem tehetünk szert gyakorlatilag hasznosítható adatokra.

A fenti megállapítás első fele azonban sajnálatos módon nem érvényes hazánkra.

Magyarországon ugyanis hivatalosan is két korszerű globális referencia rendszer képezi a lokális referenciát biztosító sík vagy síkba fejthető vetületek alapját, s akkor még nem is szóltunk arról a két korszerűtlen dátumról, melyeken alapuló kataszteri térképek még az ország jelentős részén használatban vannak. Már itt indokolt elmondanunk, hogy szigorú átszámítás két különböző dátumon alapuló sík koordináta rendszer között is csak úgy lehetséges, ha a dátumaikat is áttranszformáljuk. Míg a hagyományos grafikus (térképi) adattárolás esetén ez gyakorlatilag nem volt lehetséges addig a digitális állományokkal ez minden probléma nélkül megoldható. Ezért ma már semmi sem indokolhatja ilyen esetekben a közelítő sík transzformációk alkalmazása következtében fellépő pontosság veszteséget.

Részben a GPS alkalmazásának megkönnyítésére, részben tudományos céllal a FÖMI kutatói 5 db. HD-72 rendszerben ismert alapponton végzett GPS észlelések kiegyenlítéséből meghatározták a HD-72-ből WGS-84-be történő transzformációhoz a dc vektor három komponensét, a dµ méretarány tényezőt

és az

szögeket.

Az eredményeket a következő táblázatban foglatuk össze:

dc1 [m]	dc2 [m]	dc3 [m]	dµ ppm	^arcsec	^arcsec	^arcsec
56.15±5.53	-75.70±5.26	-16.25±5.74	1.01±0.61	-0.37±0.17	-0.20±0.22	-0.21±0.14

3.1 táblázat

A táblázatból jól látható, hogy a kapott elfordulás értékek középhibája közel megegyezik a kapott elfordulás értékekkel, ami amint már utaltunk rá, az ország relatíve kis méreteivel magyarázható.

Mivel a paraméterek kis értékek a differenciális forgatási mátrixszal dolgozhatunk, a méretarány tényező pedig µ=1+dµ, ezek figyelembe vételével, behelyettesítve az 1. táblázat értékeit a transzformációs egyenletbe a következő kifejezést kapjuk:

.

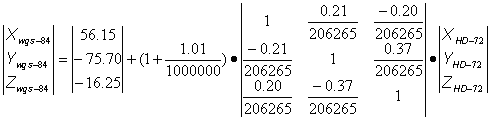Ha fordított transzformációra van szükségünk, úgy meg kell változtatnunk a dc komponensek valamint dµ előjelét, a forgatási mátrixot pedig transzponálnuk kell, ami egyenértékű azzal, hogy az átlón kívüli elemek előjelét megváltoztatjuk azaz:

.

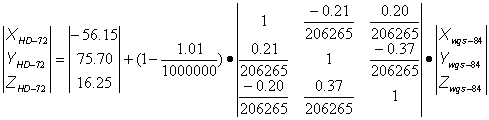Megjegyzés: Újabban több, mindkét rendszerben ismert alappont vizsgálata alapján Takács Bence 2000-ben készült diplomatervében a következő átszámítási paramétereket határozta meg:

dc1 [m]	dc2 [m]	dc3 [m]	dµ ppm	^arcsec	^arcsec	^arcsec
61.301±0.007	-68.604±0.007	-4.462±0.007	2.0404±0.05	-0.1359±0.016	-0.1855±0.021	-0.5024±0.012

Lokális referencia rendszerek

Mivel a térbeli objektumok hagyományos analóg tárolója a térkép egy sík papírlap vagy műanyag fólia, s mivel a különböző számítások a síkon sokkal egyszerűbbek mint az ellipszoidon a gyakorlatban az esetek többségében a térbeli alakzatok síkba vetített képeivel dolgozunk.

A vetítést úgy célszerű elvégezni, hogy az objektumok alakja, méretei és kölcsönös helyzete lehetőleg minél kevésbé torzuljon. A jól megválasztott vetületi rendszer többek közt azzal az előnnyel is rendelkezik, hogy a földi geodéziai szögméréseket (melyeket tulajdonképpen az ellipszoidon végeztünk) közvetlenül felhasználhatjuk a síkkoordináták számítására ( távolságok esetében ez az állítás csak azzal a korrekcióval igaz hogy néhány száz métert meghaladó távolságok esetén redukálni kell azokat a tengerszintre és a mért értékeket vetületi javítással is el kell látni).

A síkvetületeket úgy is elképzelhetjük, hogy egy a koordináta tengelyekkel párhuzamos hálóval fedjük le a területet. A koordináta rendszer kezdőpontja és pozitív X tengelyének iránya meghatározó a vetület számára.

A síkvetületet vetületi egyenletekkel határozzuk meg. Ezek az egyenletek kapcsolatot teremtenek a derékszögű koordináták és a földrajzi koordináták között, ezen kívül megadják a vetületi meridián konvergencia és a mért hosszakhoz tartozó redukció értékeit is. A geodéziában használatos vetületek 10 km alatti irányok esetében nem igényelnek redukciót a mért irányokba.

Illusztrációként közöljük a hazánkban polgári használatra hivatalos Egységes Országos Vetületi Rendszer néhány jellemzőjét. A téma iránt érdeklődőknek magyar nyelven az [5]-ben található rövid összefoglalást illetve a [6] monográfiát ajánljuk.

Meghatározás szerint az EOV a gömb süllyesztett ferde tengelyű hengervetülete. Ez a meghatározás mindenek előtt azt jelenti, hogy nem közvetlenül a hengerre vetítik a helyileg tájékozott ellipszoidot, hanem először egy olyan gömbre, mely egy parallelkörben érinti.

Mielőtt tovább megyünk néhány szóval meg kell magyaráznunk a helyi tájékozás fogalmát. Arról van szó hogy úgy helyezték el az UGGI/67 nevű forgási ellipszoidot (a=6378160 m., b=6356774,504) a Föld forgástengelyével közel párhuzamosan a Föld tömegközéppontjához képest, hogy Magyarország területén minél jobban közelítse a geoidot. A dátum eltolási és elfordulási adatai valamely globális rendszerhez pld a WGS-84-hez képest ismert ellipszoidi pontokon végzett GPS észlelések segítségével az előző alpontban ismertetett térbeli transzformációval határozhatók meg.

Az ellipszoidot a gömb az ellipszoid

szélességű parallelkörében érinti. A megfelelő gömbi parallelkör szélessége:

.

A gömb sugara az ellipszoidból levezethetően R = 6379743,001.

Mivel az EOV rendszer kezdőmeridiánját a Gellérthegyen lévő alapponton keresztül vették fel, melynek ellipszoidi szélessége L_kezdo=19^o 02’ 54.8584’’ a wgs84 ellipszoidról az UGGI 67 ellipszoidra átszámított hosszúságokból ki kell vonni L_kezdo értékét, azaz L=L_atszamitott - L_kezdo.

Amint már említettük a kettős vetítés során először az ellipszoidi szélességet és hosszúságot vetítjük a gömbre az alábbi egyenletekkel:

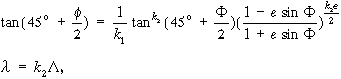
ahol k₁ = 0,9968996335, k₂ =1,000719704, e² =0,006694605.

A következő lépésben egy úgynevezett segédegyenlítőt vezetünk be, mely síkja szöget zár be az egyenlítő síkjával.

Az eredeti gömbi szélességek és hosszúságok és segédegyenlítői megfelelőik között a következő összefüggések írhatók fel:

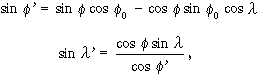
illetve:

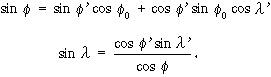
Végül áttérhetünk a vetület derékszögű síkkoordinátáinak számítására:

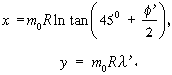
Az m₀=0,99993 érték a vetület süllyesztését szabályozza.

3.6 ábra - geodéziai síkvetület koordinátarendszer

Jelöljék X, Y a koordináták 100 km.-es egységben kifejezett értékét (azaz X = x10^-5 ), a vetületi meridiánkonvergenciát azaz a P pontbeli meridián képe pontbeli érintőjének szögét az X tengellyel (lsd. 3.6 ábra) a következő kifejezés szolgáltatja: µ"=3479.496Y + 58.6959XY - 0.47255Y^3 + 1.4176X^2Y - 0.0263XY^3 + 0.0263X^3Y - 0.0010X^2Y^3 + 0.0005X^4Y + 0.0001Y^5

A másik, vetület specifikus egyenlet a felszínen mért és a vízszintesre és tengerszintre redukált távolságokat (s) alakítja át vetületi távolsággá (d) az alábbiak szerint:

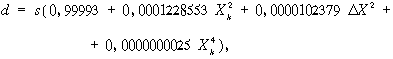
ahol az indexek a 3.6 ábrának megfelelően a távolság kezdő és végpontját jelölik.

A gyakorlatilag használt EOV koordináták azonban nem azonosak a közölt x, y derékszögű sikkoordináta értékekkel, ugyanis teljesen praktikus okokból (hogy az x és y ne legyen negatív és hogy ne is lehessen azokat felcserélni) a képletből számított x-hez 200 km-t, az y-hoz pedig 650 km-t hozzáadtak. Azaz:

X_EOV = x + 200000.000 m,
Y_EOV = y + 650000.000 m.

A lokális magassági referencia rendszer elvileg nem különbözik a globális magassági referencia rendszert képviselő geoidtól. A gyakorlatban azonban a geoidnak számtalan megjelenési formája van annak következtében, hogy az adott rendszerben melyik tenger, mely pontjának, milyen idő intervallumra vonatkoztatott közép tengerszintjét tekintik a kérdéses geoid egy rögzített pontjának. A gyakorlatban, mérési hibák következtében még az is előfordul, hogy a kiválasztott pont még elvileg sem azonos valamely tengerszinttel.

Problémát csak az jelenthet, ha két különböző referencia rendszerre vonatkoztatott magasságokat akarunk együttesen kezelni és nem ismerjük a két rendszer kiinduló pontjainak magasságkülönbségét. A probléma megoldásához elvileg csak egy olyan pont ismerete szükséges, melynek magassága mindkét rendszerben ismert. Gyakorlatilag néhány közös pont birtokában a két rendszer magasságkülönbségét a pontonkénti eltérések számtani közepéből nyerhetjük.

Magyarországon 1952-ig, az Adriai tenger 1875-ben Triesztnél kijelölt középtengerszintjére alapozott magassági referencia rendszer volt használatban, Az érdekesség kedvéért megemlítjük, a dátum a színtezési hibák következtében eltért a választott kezdőpont szintjétől és magasságát fizikailag a nadapi szintezési főalappont rögzítette ( az alapszintfelület 173,8385 méterre a jel alatt helyezkedik el a pont függővonalán). Az 1952-től bevezetett Balti magasság alap-színtfelületét a kronstadti híd lábában elhelyezett vízmérce nulla vonása jelöli ki. A két magassági referencia rendszer között az alábbi képlettel végezhetjük az átszámítást:

H_Balti = H_Adriai - 0.675 m.

Alapműveletek a vízszintes lokális referencia rendszerben

A lokális referencia rendszerben a földi pontok helyzetét derékszögű síkkoordinátákkal jellemezhetjük.

Hagyományos mérőeszközökkel végrehajtott méréseink során azonban poláris rendezőket szögeket és távolságokat mérünk. A poláris és derékszögű koordináták közötti átszámításra ezért gyakran van szükségünk a koordináta meghatározások során.

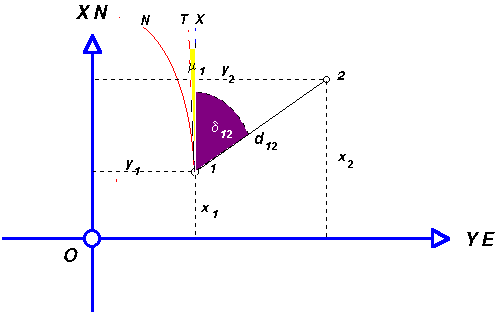
A direkt művelet (vagy hagyományos nevén elsô geodéziai főfeladat a síkon) alkalmazása esetén ismerjük az 1 pont x₁, y₁ derékszögű koordinátáit, megmértük a d₁₂ távolságot és meghatároztuk a irányszöget (azt a szöget melyet a koordináta rendszer pozitív X tengelye az óramutató járásával megegyezően leír ha az 12 egyenessel párhuzamos helyzetbe forgatjuk).

Az irányszöget közvetlenül nem tudjuk mérni hanem rendszerint ismert kezdő és végponti koordinátákkal rendelkező irányhoz csatlakozó mért szögből vezetjük le. Az irányszög meghatározásának másik ritkábban használt módja ha egy giroteodolitnak nevezett különleges műszerrel (lsd. [5]) megmérjük az irány valódi északkal bezárt szögét az úgy nevezett azimutot és ebből levonjuk a pontbeli vetületi meridián konvergenciát µ-t (lsd. 3.6 ábra).

A 2 pont keresett koordinátáit az alábbi kifejezésekből nyerjük:

.

A fordított feladat (hagyományos nevén második geodéziai főfeladat a síkon) azt a célt szolgálja, hogy egy irány két végponti koordinátáinak x₁, y₁-nak és x₂, y₂-nek az ismeretében kiszámítsuk a pontok távolságát d₁₂-t és az általuk alkotott irány irányszögét -t. A megoldást az alábbi képletek segítségével kapjuk meg :

,

.

Napjainkban a lokális vízszintes és magassági referencia rendszer alappontjait még külön állandósítják.

A legtöbb országban mind a lokális vízszintes referencia rendszer ismert koordinátájú alappontjait mind a magassági alapponthálózatot az állami geodéziai szolgálat hozza létre, határozza meg és tartja karban.

A vízszintes alappontok földalatti jellel ellátott beton tömbök, melyekbe furatos rézcsapot betonoznak. A tulajdonképpeni pontot a furatos rézcsap jelöli. A rendszerint 15x15 cm keresztmetszetű 60 cm magas tömböket úgy ássák el a földbe, hogy alattuk a biztonság kedvéért, még egy szintén furatos betonlap is jelölje a pontot. A két furatnak természetesen egy függőlegesben kell elhelyezkednie. Sziklás talajon a csapot a sziklába betonozzák, városokban gyakran alkalmaznak tetőpilléreket, szegélykőbe betonozott csapokat stb. Magyarországon az alapponthálózat gerincét alkotó pontokra vasbeton mérőtornyokat is építettek.

A magassági alappontokat gyakran helyezik el műtárgyakba (hídpillérek), épületek lábazataiba. Ha a szintezési vonal közelében nincsenek építmények úgy a talajba lesüllyesztve monolit vasbeton pillért építenek és abba helyeznek el 2-3 magassági alappontot. Sziklás talaj esetén az alappontokat közvetlenül a sziklába betonozzák. Maguk az alappontok szférikus fejű fém betételemek (pld. gömbölyű fejű szögecsek), melyek legfelső pontja képviseli a kérdéses magasságot.

A vízszintes és magassági alappontok sűrűsége átlagosan azonos, de függ az országtól és a földhasználati övezettől. Mezőgazdasági hasznosítású külterületen Európában a pontok sűrűsége 7 és 1.5 km között változik. Ipari és lakott körzetekben a pontok sűrűsége jelentősen megnő és a helyi körülmények függvényében 1.5 km és néhány száz méter között ingadozik.

Az alappontok pontos helyét rögzítő helyszínrajzi leírásokat a pontok koordinátáival illetve magasságaival együtt Magyarországon a területileg illetékes földhivatalban lehet beszerezni.

· a következő részben a földi felmérés módszereit tekintjük át

· esetleg visszatérhet az előző részhez

· illetve a tartalomjegyzékhez

---

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc

---