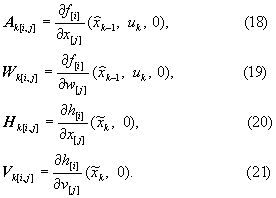GIS alkalmazások II (1)
Intelligens gépjármű navigációs rendszerek
A fejezet bevezetésében először röviden bemutatjuk a témához kapcsolódó fogalmakat, a rendszerek és koncepciók fejlődését, az amerikai Nemzeti Intelligens Közlekedési Rendszer (ITS) Infrastruktúra fölvázolásával zárva a témát.
A részletes tárgyalás során ismertetjük a rendszerek főbb alkotóelemeit: a digitális térképeket ezen belül is a GDF adatszabványt, az AVL (Automatic Vehicle Location = Automatikus Jármű Helymeghatározás) technikák alapját jelentő GPS-DR szenzor integrációt és ehhez kapcsolódóan a száloptikás interferométeres giroszkópot, valamint a mikrogépészeti vibrációs giroszkópot, a szenzor integrációt matematikailag támogató Kálmán szűrőt, a térkép illesztés (map matching) szerepét a navigáció finomításában, illetve a rendszerek továbbfejlesztési lehetőségeit a mobil telefon rendszerek felhasználásával, a távközlési technikákat, melyekre a különböző AVL alkalmazásoknak más és más szempontból van szüksége.
Tárgyalásunkat néhány fontos fejlődési irány összefoglalásával zárjuk.
Bevezetés
A közúti közlekedés rohamos fejlődésének hatására a 70-es évek végén Japán elindította a CACS (Comprehensive Automobile Control System = Átfogó Autóirányító Rendszer) nevű kutatási projektet, melynek az volt a célja, hogy egy központosított számítógépes rendszer az út mellett felszerelt adó-vevők segítségével vegye a gépkocsikból érkező úti cél kérelmeket és a kérés központosított feldolgozása után továbbítsa az eredményt - az úticél eléréséhez szükséges útirányokat - a vezetők felé.
A következő kutatási téma Japánban a 80-as években indult. Az ebben a RACS (Road Automobile Communication System = Úti Auto Kommunikációs Rendszer) nevű projektben kidolgozták azt a Japánban máig érvényben lévő navigációs alapelvet, hogy a gépkocsi navigációt az út melletti távközlési szerelvények (beacons = bóják) felhasználásával egy rendszer központ segítségével valósítják meg a gépkocsik. Ugyanakkor ez a rendszer már feltételezte, hogy a gépkocsi pillanatnyi helyzetét a beépített szenzorok határozzák meg.
Míg Japánban a témát központi, államilag finanszírozott kutatási témák indították be, addig Európában a kezdeményező a gépkocsi gyártó ipar volt. Az első tapogatózó fejlesztési kísérleteket a BOSCH kezdeményezte a korai 80-as években. Szerencsére Európában nem csak a gépkocsiba építendő hardver fejlesztését kezdték meg, hanem már az első időkben rájöttek arra, hogy digitális térképek nélkül a gépkocsi navigáció nem sokat ér. 1983-tól kezdődően számos nyugat európai egyetemi tanszék (közöttük a vezető szerep kétségtelenül a Hannoveri Egyetem Kartográfiai Intézetéé volt) látott hozzá a digitális közlekedési térképek elméleti alapjainak kidolgozásához.
1986 és 1989 között a Közös Piac EUREKA programjának DEMETER nevű projektjében a BOSH és a PHILIPS részvételével kidolgozták a GDF (Geographic Data File) nevű digitális úttérkép szabvány és formátum első verzióját. 1989-1992 között a DRIVE I projekt keretében, a GDF felhasználásával megkezdték kísérleti szakaszokon az európai digitális úttérkép elkészítését. A gyakorlati térképkészítés tapasztalatait felhasználva elkészítették a GDF második verzióját. A munkát a DRIVE II projekt keretében folytatták 1992-1994 között.
A továbbiakban, a tervezett DRIVE III projekt nem valósult ugyan meg, de az európai digitális úttérkép készítését - kereskedelmi alapon - tovább folytatták. A digitális térképezésben érdekelt cégek mint az ERTICO nevű európai non-profit its szervezet partnerei továbbfejlesztették a GDF-et is (3. verzió - 1996) azzal a céllal, hogy nemzetközi szabványként elfogadtatva azt növelhessék piaci részesedésüket. Sajnos az EU 4. illetve 5. kutatási keretprogramja keretében futó közlekedést érintő "telematikai" kutatásokról nem tudok beszámolni, mivel a témákat tartalmazó WEB oldal üres.
Az EU intelligens közlekedési rendszereket illető politikájával kapcsolatban utalnunk kell az ERTICO honlapján található oldalra, mely arról számol be, hogy 1997 június 17.-én a miniszterek tanácsa elfogadta a Bizottság előterjesztését a közúti közlekedési telematika létrehozására vonatkozó stratégiáról és cselekvési keretekről. A kérdéses dokumentumban felsorolt öt elsőbbséget élvező téma közül az ötödik így szól "Rendszer Architektúra: az a cél, hogy meghatározásra kerüljön az európai nyílt rendszerű architektúra". Mivel ez a határozat 1997-es, az európai its szervezet - az ERTICO honlapján pedig semmi újabb sincs az európai its architektúrára vonatkozóan sajnos úgy néz ki, hogy ilyen nincs. Ezzel magyarázható, hogy az its infrastruktúra, illetve az annak részét képező architektúra rövid felvázolását az Egyesült Államok példáján tudjuk csak megtenni.
Míg Európában a digitális térképezés és ezen belül a digitális úttérképek készítése gyakorlatilag a gépkocsi navigációs igények stimulálására indult be, addig az Egyesült Államokban a topográfiai térképek biztosításáért felelős állami ügynökség a USGS és a Census Bureau (Népszámlálási Hivatal) a 80-as évek elejétől megkezdték a digitális topográfiai, népszámlálási és ez utóbbin belül városi térképek (úgy nevezett DIME fájlok) előállítását. Ugyanakkor ezek a térképek nem direkt út-térképek voltak ezért a különböző területi illetőségű útügyi, városi, egészségügyi, szállítmányozási, stb. szervezetek igyekeztek a geometriához kapcsolódó leíró adataikat a saját elképzelésük szerint kialakítani. A használhatóságot is akadályozó heterogenitás kiküszöbölése érdekében a korai amerikai its kutatási projektek mint például a Pathfinder vagy a Trav Tek egységes területi Közlekedési Műveleti Központok kialakítását koncepcionálták.
A jelenleg is aktív, 1986-ban megkezdett Kaliforniai PATH projekt azt a célt tűzte ki, hogy elméletileg megalapozza azoknak fejlett technológiáknak a széleskörű alkalmazását, melyekkel gyökeresen megjavítható Kalifornia szárazföldi közlekedése. Ezen belül a kutatás három fő területre vonatkozik: az ATMIS-re (fejlett közlekedés üzemelési és információs rendszerre), az AVCS-re (fejlett jármű vezérlő rendszerre), illetve a rendszer kutatásra, mely a két alrendszer területén elért eredményeket integrálja.
Ami az első alkalmazásokat illeti, Európával és Japánnal ellentétben, ahol a személyautó navigációra helyezték a főhangsúlyt, az Egyesült Államokban a nagy gépkocsi parkkal rendelkező szolgáltatók és szállítási vállalatok (mentők, rendőrség, tömegközlekedés, teherfuvarozók, stb.) útvonal szervezési feladatainak automatizálása, az úgy nevezett "flotta menedzsment" feladat megoldása kapott prioritást. Ezzel is magyarázható. hogy a korai amerikai publikációkban az adatbázisok kérdései valamint a távközlési megoldások döntő szerepet kaptak.
Az ITS (Intelligent Transportation System = Intelligens Közlekedési Rendszer) számtalan komponensből tevődik össze. A legtöbb része témánkon kívül esik. Ide tartozik például a forgalom számlálás, a forgalomirányító lámpák optimális ütemezése, a balesetek automatikus jelentése, a követési távolság automatikus betartása, a flotta menedzsment, az automatikus díjfizetés, a turisztikai információk szolgáltatása, a torlódás mentes útvonalak kijelölése, stb., stb.
Világos, hogy a többé-kevésbé izolált műszaki kutatások egy bizonyos szintje után az alrendszerek optimális megvalósítása csak egységes rendszerben lehetséges. Ezt szolgálja a címben szereplő nemzeti its infrastruktúra, mely nem más mint egy rendszer terv, kidolgozói a Lockhid Martin nevű fegyvergyár és az America ITS nevű társadalmi szakmai szervezet. A munka költségeit az Egyesült Államok Közlekedési Minisztériuma és a Szövetségi Út Adminisztráció biztosították.
Az architektúra tartalmazza
- az its funkciókat (pld. forgalmi adat gyűjtést vagy útvonal kijelölési kérelmet);
- azokat a fizikai eszközöket vagy alrendszereket, melyek a funkciókat tartalmazzák (pld. gépkocsi vagy út menti szerelvények);
- az információ folyamokat, melyek ezeket az elemeket rendszerré integrálják.
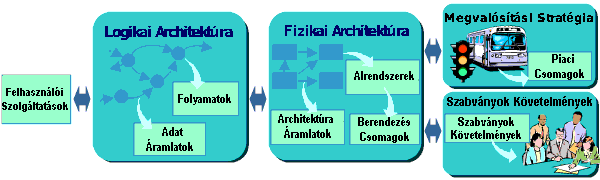
Rövid összefoglalónkban felvázoljuk a rendszerterv legfontosabb összetevőit (6.53 ábra), felsoroljuk a rendszer szolgáltatásait a felhasználók számára, és végül bemutatjuk a rendszer fizikai alkotóinak (alrendszereinek) blokkvázlatát (6.54 ábra), mely segítségével megítélhetjük, hogy az általunk tárgyalt navigációs feladat milyen szerepet játszik az egész rendszerben.
|
6.53 ábra - az its architektúra legfontosabb csomópontjai
|
A felhasználói szolgáltatásokat hét nagy csomagba foglalja a terv:
- Utazás és Forgalom Szervezés
- Az Indulás Előtti Utazási Információk segítik az utazókat, hogy még az utazás megkezdése előtt kiválaszthassák az utazás módját, megbecsülhessék a szükséges utazási időt és dönthessenek a legalkalmasabb útvonalról. A csomag négy fő funkciója
- Információ a Rendelkezésre álló Szolgáltatásokról;
- Információ az Aktuális Helyzetről;
- Útvonal Tervező Szolgálat és
- Hozzáférés biztosítása a szolgáltatásokhoz.
- Az Menet-közben Nyújtott Információk a Vezetőnek lehetővé teszik az útvonal alternatívák közüli választást. Fő funkciói:
- A Vezetői Tanácsadás és
- A Gépkocsin Belüli Forgalomirányító Kijelzés.
- Az Útvonal Irányítás megadja az útvonalat a választott útcélokhoz. Főbb funkciói:
- Az útvonal megadás;
- A Statikus Üzemmód;
- A Jelenidejű Üzemmód és
- A Felhasználói Interfész.
- Az Úticél Illesztés és Helyfoglalás három fő függvénye:
- Az Utazó Kérése;
- Az Utazást Biztosító Szolgáltatása és
- Az Információ Feldolgozása.
- Az Utazási Szolgáltatások Információja lényegében "Arany Oldalak" jellegű információt biztosít az utazóknak
- az Információ Átvétel és
- az Információ Elérés
függvények keretében.
- A Forgalom Irányítás feladata az utak és utcák forgalmának hatékony kezelése. Feladatát négy funkció segítségével oldja meg, ezek
- a forgalom áramlás optimalizálása;
- a forgalom felügyelet;
- a vezérlési funkció és
- az információ szolgáltatás.
- A Közlekedési események kezelése a következő hat funkció keretében realizálódik:
- a tervezett események;
- az események azonosítása;
- válasz akciók megfogalmazása;
- a válasz akciók koordinált megvalósításának támogatása;
- az akciókra adandó válaszok kezdeményezésének támogatása;
- a vészhelyzetek előrejelzése.
- A Közlekedési igények kezelése a
- közlekedési rendszer hatékonyságának javítása és
- a mobilitási lehetőségek széles skálájának biztosítása
funkciók segítségével valósul meg.
- Emisszió tesztelés és csökkentés egyetlen azonos nevű funkcióval rendelkezik.
- Az út-vasút keresztezési szolgáltatás azonos nevű függvénye külön kezeli az alacsony és nagysebességű vasutakkal való találkozást.
- Tömegközlekedés Szervezés
- Tömegközlekedés Szervezés
- Menet közbeni menetrendi és foglaltsági információ a csatlakozásokról
- Személyre szabott tömegközlekedés
- Tömegközlekedés Biztonsága
- Elektronikus Fizetés
- Elektronikus Fizetési Szolgáltatások
- Kereskedelmi Gépjármű Műveletek
- Kereskedelmi Gépjármű Elektronikus Kezelése
- Automatizált Útmelletti Biztonsági Felügyelet
- Fedélzeti Biztonsági Monitorozás
- Kereskedelmi Gépjármű Adminisztratív Eljárásai
- Válasz a Veszélyes Anyaggal Történt Eseményre
- Kereskedelmi Flotta Menedzsment
- Baleset Kezelés
- Baleset Közlés és Személyes Biztonság
- Mentőautó Menedzsment
- Fejlett Gépkocsi Biztonsági Rendszerek
- Hossz-irányú Ütközés Elkerülés
- Oldal-irányú Ütközés Elkerülés
- Kereszteződési Ütközés Elkerülés
- Látás Javítás az Összeütközés Elkerülésére
- Biztonságra Készültség
- Összeütközést Megelőző Automatikus Fékezés
- Automatizált Gépjármű Műveletek
- Információ Menedzsment
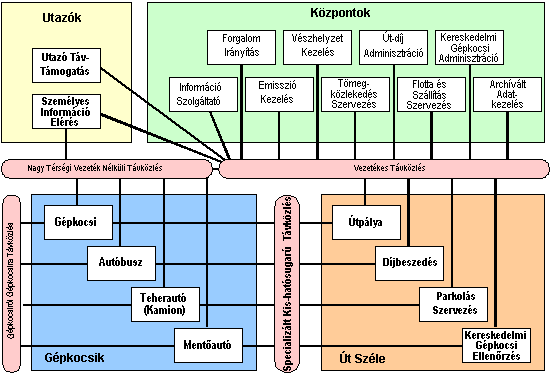
Bár az első szolgáltatási csomag kivételével nem vázoltuk fel az egyes szolgáltatások funkcióit, reméljük hogy a szolgáltatások nevei is utalnak azokra a területekre, ahol a gépkocsi helymeghatározásra döntő szerep hárul. A következő ábrán bemutatjuk a fizikai alrendszereket és a közöttük fellépő távközlési kapcsolatokat.
|
6.54 ábra - az its architektúra fizikai alrendszerei
|
Az ábrával kapcsolatban kiegészítésképpen megjegyezzük, hogy "mentőautó" alatt minden vészhelyzetben eljáró gépkocsit, tehát rendőr, tűzoltó, autómentő, stb. gépkocsit kell érteni.
A továbbiakban tehát arra kívánunk választ adni, hogy miként tudja a gépkocsivezető a gépkocsiban menetközben azonosítani a pillanatnyi helyzetét, e helyzet valamint a rendeltetési hely ismeretében, miként tudja meghatározni a követendő útvonalat, hogyan értesül a teherautó flotta diszpécsere a teherautók pillanatnyi helyzetéről és hogyan tud intézkedni a helyzet dinamikus megváltoztatása érdekében. Még számtalan egyéb funkciót is felsorolhatnánk (pld. hogyan biztosíthat az úton lévő magának megfelelő szállást és hogyan talál oda), a technika a legtöbb esetben hasonló, a különbség csak az elérendő adatbázisokban van.
Digitális Úttérképek
A gépkocsi navigáció céljait szolgáló úttérképek a tárolási kapacitással való takarékosság érdekében újabban a vektoros adatmodellt, azon belül is a topológiai adatmodellt használják. Ezt az adatmodellt csomópontok és az azokat összekötő ívek határozzák meg. A rendszer geometriáját az ívek töréspontjainak valamint a csomópontoknak a koordinátái határozzák meg, míg a modell logikája a ívek csomópontokat összekapcsoló összeköttetési információin nyugszik. A harmadik információ elemet az ív-szakaszok, ívek, csomópontok tulajdonságait leíró táblázatok alkotják. Ez utóbbiak igen nagyszámúak is lehetnek, ezért a következő ábráinkon nem törekedhetünk a teljességre, csak illusztrációként mutatunk be néhány attribútum típust.
Ahogy az adatmodellek kapcsán már kifejtettük a legutolsó időkig leggyakrabban alkalmazott georelációs adatmodellben a geometriát (tehát a koordinátákat) és a leíró adatokat külön adatbázisokban tárolták. A korszerű objektum-orientált rendszerekben az összes adat, tehát a geometria, konnektivitás és tulajdonság jellemzők is egy adatbázisban kerülnek tárolásra.
|
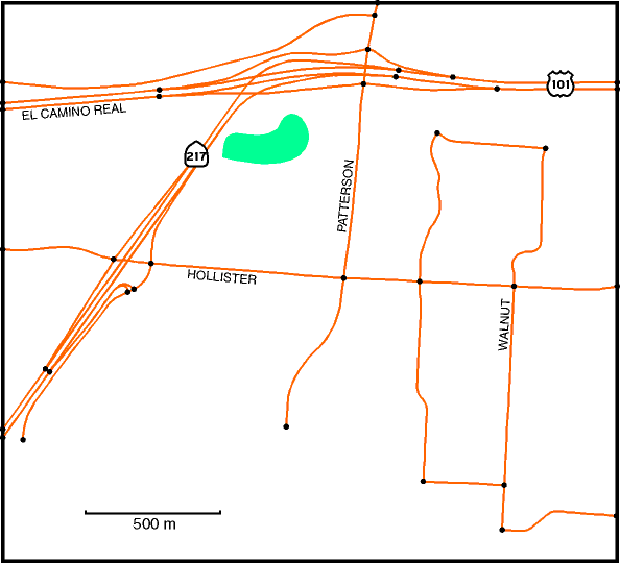
6.55 ábra - amerikai úttérkép részlet
|
|
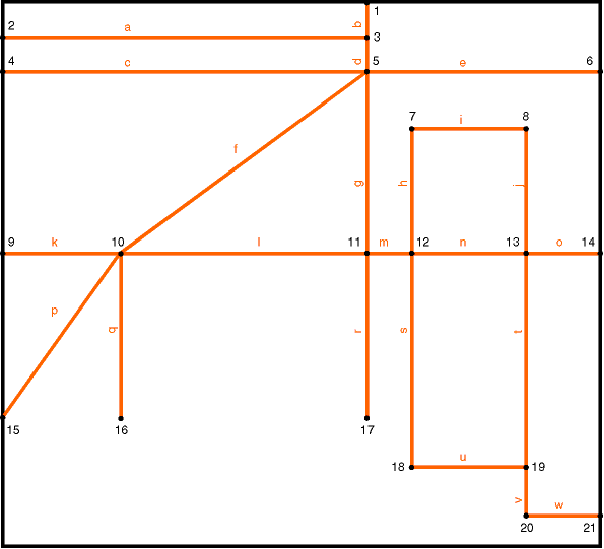
6.56 ábra - a 6.55 ábra úttérkép részletéből készített gráf
|
A 6.55 ábrán bemutatunk egy amerikai úttérkép részletet, melyen az útpályák geometriai megjelenése szerepel. A 6.56 ábrán ugyanennek az útnak a gráfját látjuk. Amint az ábrából kitűnik a gráfban csak azokat a csomópontokat tüntettük fel, melyek az élek (ívek) csatlakozása szempontjából jelentőséggel bírnak. A gráffal reprezentált logikai váz nem csak az adatmodell szervezése szempontjából lényeges hanem azért is, mivel a navigációhoz is szükséges legrövidebb út algoritmusok (mint például a már megismert Dijsktra algoritmus is) ezt használják.
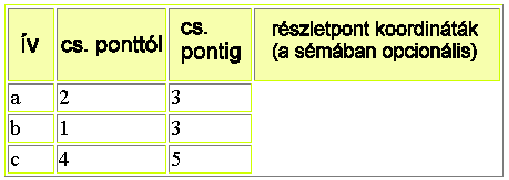
A gráfot a csomópontok és ívek attribútum táblái segítségével adhatjuk meg. A 6.57 ábrán néhány csomópont attribútumát tüntettük fel. A baloldali ábrarészben szerepelnek a csomópontok koordinátái, a jobboldaliban az összekötési információk. Amint látjuk a hálózat felépítése szempontjából a csomópontok koordinátáira nincs szükségünk.
|
|
6.57 ábra - a csomópontok attribútum táblái |
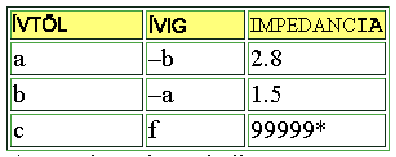
Az ívek attribútum táblázatai közül a 6.58 ábra bal oldalán található részben redundáns (a gráf szempontjából) részben opcionális, mivel a geometriát a logikai leírástól függetlenül is tároljuk. Az ábra jobboldalán található táblázat érdekessége, hogy összetett kulcsokkal rendelkezik, s egyben tartalmazza a legrövidebb út kereséshez általában használt egyetlen minőségi attribútumot az impedanciát. A táblázatokból kitűnik, hogy az ívek irányítottak, azaz kezdő és végpontjuk nem cserélhető fel. Ha az íven a végponttól a kezdőpont felé haladunk, úgy az ívet negatív előjellel kell figyelembe venni.
|
|
6.58 ábra - az ívek első attribútum táblái
|
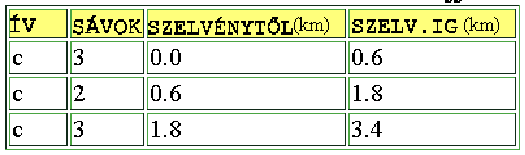
Az íveknek természetesen számtalan egyéb attribútumuk is van. Ezek közül egyesek (pld. a címek) nem az egész ívre vonatkoznak, hanem csak az ív valamely pontjára vagy szakaszára. Az ilyen attribútumok tárolását az úgy nevezett dinamikus szegmentálással végezhetjük, amikor is a kérdéses pontok helyén vagy szakaszok esetében a kezdő és végponton ideiglenes csomópontot iktathat be a GIS szoftver. Azt hogy hova kell ezt a csomópontot helyezni az ívek olyan további attribútum táblázataiból olvassa ki a program, melyek megadják a kérdéses pontok távolságát az ív kezdő csomópontjától. A korai amerikai digitális várostérképek egyszerűbben oldották meg a címek földrajzi - térképi kijelölését. A csomópontok közötti bal- és jobboldali címállományt egyenletesen interpolálták be a két csomópont közötti koordináta különbség által meghatározott távolságra. Ez a módszer természetesen csak akkor szolgáltat helyes eredményt, ha az utcák egyenesek, a címek folyamatosak és minden címhez azonos hosszúságú utcafront tartozik.

|
|
6.59 ábra - az ívek további attribútum táblái
|
Természetesen számtalan más megoldás is lehetséges. Például, gyakran a csomópontokhoz kapcsolják a kereszteződések forgalmi adatait. Számunkra egyelőre azt szükséges rögzíteni, hogy az úttérképek hálózat-típusúak, a közlekedéssel kapcsolatos leíró adatok pedig a hálózat elemeihez: az ívekhez és csomópontokhoz kapcsolhatók.
A jelenleg elterjedt digitális úthálózati térképek kétdimenziósak. Ez a tény problémát jelenthet az aluljárók-felüljárók esetén melyekről közvetlenül nem lehet rákanyarodni a szintben keresztezett útra. Ilyen esetekben viszonylag egyszerű megoldás, ha a kérdéses lekanyarodásnak igen nagy impedancia értéket adunk (6.58 ábra, jobboldali ábrarész *-al jelölt impedancia). Másik lehetőség, ha a szintbeli kereszteződésre a csomópont attribútumai között utalunk. A háromdimenziós ábrázolás hiánya különösen akkor jelentkezik, ha olyan utakon utazunk melyek egymás fölött haladnak párhuzamosan, de a felső útról mások a lehajtási lehetőségek mint az alsó útról. Ilyen esetben a kocsiban lévő navigációs berendezés nem tudja eldönteni, hogy melyik párhuzamos íven haladunk és ebből következően nem tud megfelelő vezetési instrukciókat adni. Ez a probléma csak háromdimenziós adatmodellel és háromdimenziós navigációval oldható meg. Míg az utóbbi elvileg megoldható a mobil térképezéssel kapcsolatban megismert rendszerekkel, háromdimenziós úttérképekről egyelőre nincs tudomásom.
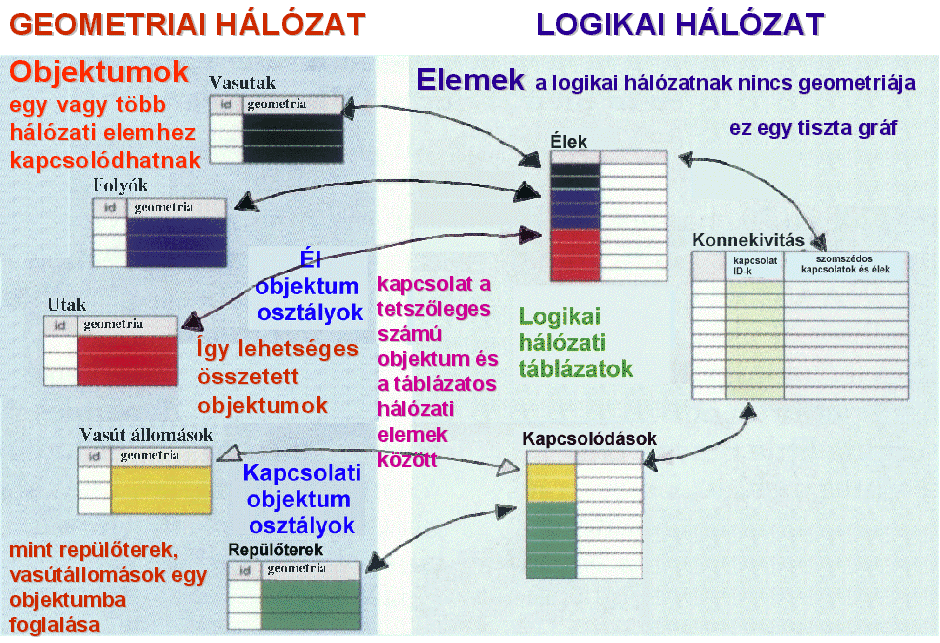
Már most utalnunk kell azonban két körülményre: a gépkocsi navigációs rendszerben installált szoftver, ellentétben sok GIS szoftverrel, rendszerint csak bizonyos előre definiált adat modell és adatformátum megjelenítésére alkalmas. Az Egyesült Államokban 1996-ban a Közlekedési Minisztérium John A. Volpe Kutatási Központja elkészítette az általunk már jól ismert SDTS rövidítésű térbeli adatátviteli szabvány Közlekedési Profiljának tervezetét [13]. Mivel azonban a digitális úttérkép szabvány tervezet kidolgozásában Európának sincs oka szégyenkezni ezért rövid ismertetésünkben a GDF adatszabványt fogjuk bemutatni. Mielőtt azonban a GDF tárgyalásába belekezdenénk két ábrán felvázoljuk a hálózatok objektum-orientált adatmodelljét is M. Zeiler, az ESRI munkatársa rövid népszerűsítő cikke alapján [14] (6.60 és 6.61 ábra).
|
6.60 ábra - az objektum orientált hálózati modell főbb összetevői
|
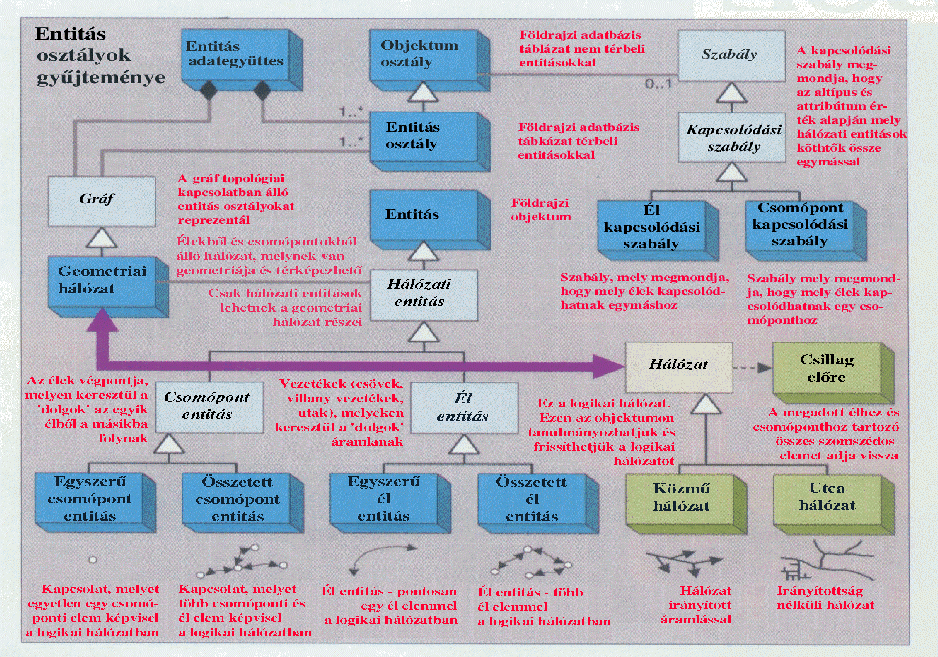
|
6.61 ábra - az objektum orientált hálózati model UML osztálydiagrammja
|
A 6.61 ábra több jelölését (generalizálás, kompozíció, aggregáció) már megismertük az Univerzális Modellező Nyelv bemutatásakor.
A GDF szabvány tervezet 3.0 verziója 1995 októberében készült el [15]. A szabvány 12 fejezetből és két mellékletből áll. A bevezetés szerepét játszó 1, 2 és 3 fejezet (hatókör, normatív hivatkozások, definíciók) után a 4. fejezet mutatja be a koncepcionális adatmodellt. Az ötödik fejezet tartalmazza a GDF-ben meghatározott objektum osztályok katalógusát. A hatodik fejezetben leírt attribútum osztály katalógus részletesen meghatározza az objektum osztályok tulajdonság jellemzőit, egyes attribútumokat konkrét objektum osztályokhoz kapcsol, más attribútumokat ennél általánosabban, több osztályhoz rendelhetően határoz meg. Megkülönböztet - ezen túl - egyszerű és összetett attribútumokat is. A hetedik fejezet olyan szemantikus kapcsolatokat definiál, melyek lehetővé teszik az információ valószerűbb közvetítését. Ilyen kapcsolat lehet például az Út Elemek és az Épületek objektum osztályok között, mely kifejezi, hogy az épület valamely út elem "mentén" helyezkedik el. Talán a legérdekesebb a nyolcadik fejezet, mely az objektumok három színtű reprezentálását határozza meg. A kilencedik fejezet útmutatást ad a GDF adatok minőségi vizsgálatára és hitelesítésére. A tizedik fejezetben található globális adat katalógus instrukciókat ad a meta adatok köztük a referencia rendszer, forrás anyagok modellezésére ez a fejezet tartalmazza az adatszótár specifikációkat is, melyek felhasználásával a GDF szükség szerint bővíthető. A tizenegyedik fejezet a modell logikai leírását tartalmazza, hasonlóan ahhoz, ahogy az EXPRESS nyelv segítségével meghatároztuk a Magyar Térbeli Adatátviteli Szabványt. A különbség elsősorban abban áll, hogy a szabvány elemeire vonatkozó típus deklarációkra az ESN (Extended Style Notation) nevű adatleíró nyelvet alkalmazták, mely a gráfelmélet eszközeivel egyszerűen modellezi a bonyolult hierarchikus típusokat. A tizenkettedik fejezet azt a rekord struktúrát írja le, melyet az adathordozón történő átvitelnél alkalmazni kell. Az A mellékletben találjuk meg az alkalmazandó kódokat, a B melléklet pedig példákat mutat be a térképek tartalmára és minőségi ellenőrzésére.
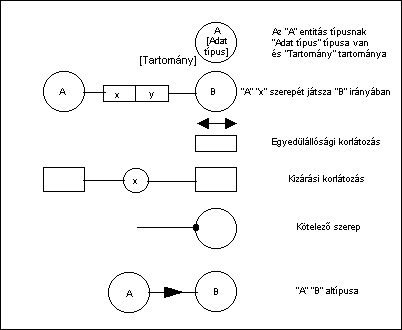
A koncepcionális adatmodellt (a szabvány általános adatmodellnek hívja) az úgy nevezett NIAM (Nijsen's Information Analyzis Method) diagrammok segítségével mutatja be a szabvány. Ezek a diagrammok tulajdonkeppen sajátos jelölés rendszerrel rendelkező Entity-Relationship (ER) diagramok. A 6.62 ábra tartalmazza azokat a legfontosabb rajzi elemeket, melyeket a szabvány felhasznál.
|
6.62 ábra - a NIAM diagramok legfontosabb jelölései
|
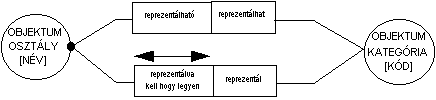
A jelölések közül talán a legnehezebb magyar szavakkal leírni az objektumok kölcsönös szerepjátszásait. A 6.63 ábrán számtalan ilyen szerep meghatározást látunk, tekintsük például az attribútum és az objektum egymással kapcsolatban játszott szerepét. Ha az attribútum oldaláról indulunk ki akkor a kijelentés úgy olvasandó, hogy "attribútuma az objektumnak". Angolul ez jobban hangzik, mert akkor a -nak a helyén of van és az "attribute of object" szórendileg is helyes birtokviszony, míg magyarban helyesen előbb a birtokosnak utána a birtoknak kellene szerepelni. Nyelvtani különbözőségből adódó nehezebb áttekinthetőséget találunk a 6.65 ábran is, az "is" és "of" szerep párral kapcsolatban. Az eredeti kifejezés azt mondja: "Feature Class is Partner" illetve a fordított állítás: "Partner of Feature Class", ami rossz magyarsággal azt jelenti, hogy " az Objektum Osztály (van) Partner" illetve, hogy "Partnere az Ojbektum Osztálynak".
Lássuk ezután az általános adatmodellt a 6.63 ábrán.
|
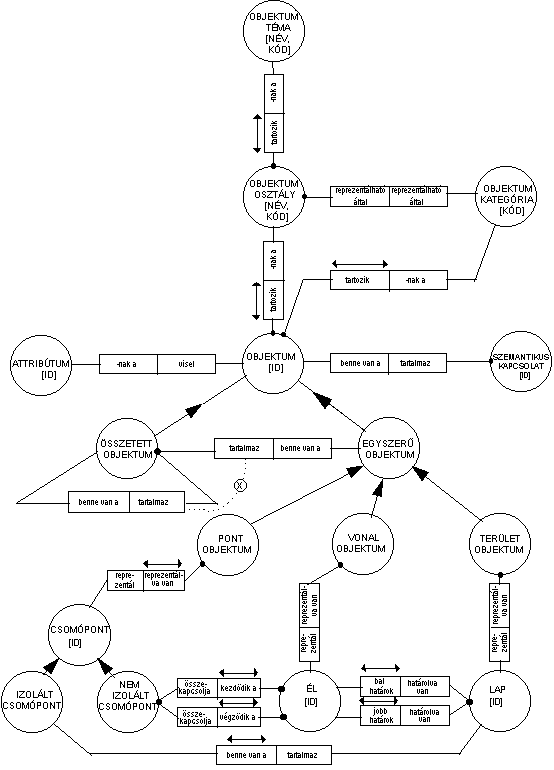
6.63 ábra - a GDS általános adatmodellje
|
A modell középpontjában az objektum található, mely olyan földrajzi entitás, melynek térbeli helyzete van, mint például egy út vagy egy ház. A diagramban található objektum tehát konkrét. Minden objektum tartozik egy bizonyos objektum osztályhoz. Ami azt jelenti, hogy egy objektum nem tartozhat több osztályhoz, illetve, hogy osztályhoz nem tartozó objektum nincs megengedve. Ezt a korlátozást az a fekete pont reprezentálja, mely az objektum körére illeszkedik a "tartozik" szerep állításnál. Ugyan e "tartozik" fölött lévő nyilakban végződő egyenes pedig az egyedülállósági korlátozást reprezentálja, azaz, hogy az objektum csak egy osztályhoz tartozhat.
A diagramból a továbbiakban az is kiderül, hogy minden objektumnak lehet zérus, egy vagy több attribútuma, és szemantikus kapcsolatban állhat egy vagy több objektummal.
Minden objektum pontosan egy objektum kategóriához tartozhat, melyek a következők: Pont, Vonal, Terület, Összetett. Annak a konzekvenciái, hogy az objektum valamely kategóriához tartozik a rajz alján láthatók. Itt láthatók az egyoldali nyíllal ábrázolt altípus korlátozások: a Pont objektum altípusa az Egyszerű objektumnak, ez utóbbi altípusa az Objektumnak. Látható továbbá, hogy a Pont objektumot mindég egy Csomópont képviseli, a Vonal objektumot egy vagy több Él, a Terület objektumot pedig egy vagy több Lap. Az Él és csomópont kölcsönös kapcsolatban állnak.
Az Objektum Katalógus az objektum osztályokat definiálja, de az egyszerűség kedvéért objektum osztályok helyett objektumokról beszél. Ahogy már említettük, a rajzból látható, hogy minden objektum egy objektum osztályhoz és egy objektum témához tartozik, melyeknek egyedi neveik és kódjaik vannak. A rajzból az is kiderül, hogy bizonyos objektumok egy vagy több másik objektumból kerülnek kialakításra. Ezeket az objektumokat nevezik Összetett Objektumoknak. Például az Út Út Elemeket tartalmazhat.
|
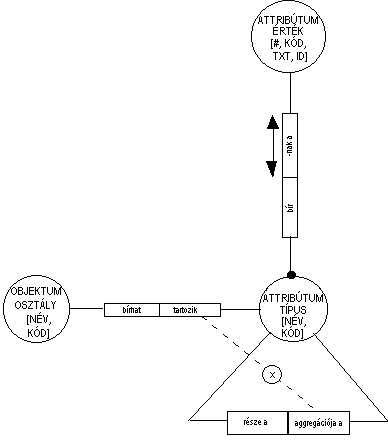
6.64 ábra - az attribútumok adatmodellje
|
Az Attribútum Katalógus attribútum típusokat neveiket és kódjaikat határozza meg (6.64 ábra). Megadja azokat az objektum osztályokat, melyekhez egy bizonyos attribútum típus hozzákapcsolható. Az ábra bemutatja, hogy egy attribútum más attribútumok gyűjteményéből is állhat. Az ilyen attribútumot Összetett Attribútumnak nevezik. Bizonyos attribútum típusok, melyeket az Összetett Attribútumok képzésére használnak közvetlenül nem kapcsolhatók objektumokhoz. Ezt mutatja az ábrán a kizárási korlátozás (x).
|
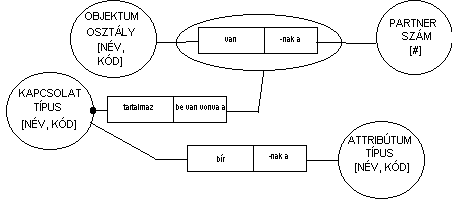
6.65 ábra - az objektumok közötti kapcsolatok adatmodellje
|
A Kapcsolat Katalógus olyan jelentős kapcsolatokat tartalmaz, melyek kettő vagy több objektum között realizálódnak. A kapcsolatban résztvevő objektumok nem feltétlenül tartoznak különböző osztályokhoz. Azokat a kapcsolatokat, melyekben mind A mind B egyedenként azonos osztályhoz tartozik és közös jelentésük van kapcsolat típusokba sorolják. Egy konkrét kapcsolat típust egyértelműen meghatároz a neve vagy a kódja (6.65 ábra). A kapcsolatok rendszerint két objektum között jönnek létre, de vannak esetek amikor több objektum is részt vesz a kapcsolatban. Ilyenkor az egyes objektum típusok sorrendje is lényeges. Ezért szerepel az ábrán a PARTNER SZÁM [#], mely meghatározza a kapcsolatban résztvevő típusok sorrendjét.
|
6.66 ábra - az objektumok reprezentációjának adatmodellje
|
Az Objektum Reprezentációs Séma konkretizálja az entitás osztályok leképezését a GIS rendszerek által kezelt objektumokra. Négy térbeli objektumot ismer a szabvány, melyek a következők: pont, vonal, terület és összetett.
A megfeleltetés során egy-egy entitás osztály vagy minden példányával azonos objektumra képződik le, vagy az osztály egyes példányai az egyik, más példányai a másik objektum felhasználásával reprezentálódnak (6.66 ábra). Ez utóbbi esetben a Séma leírja, hogy milyen esetekben milyen reprezentációra van szükség.
Globálisan a GDF két reprezentációs szintet deklarál. Az Első Reprezentációs Szint
pontokat, vonalakat és területeket használ a megfeleltetéshez, a Második Reprezentációs Szinten
összetett objektumok képviselik az entitásokat. A szabvány ezek mellett beszél még a Nulladik Reprezentációs Szintről
is, mely tulajdonképpen az egyszerű entitások geometriáját és topológiáját írja le, ez utóbbit síkbeli gráfokkal.
A gdf fájl az utak statikus jellemzőit írja le, több mint száz attribútummal. Sok alkalmazás azonban dinamikus információt is igényel. Az utóbbi évek fejlesztései ezekben az alkalmazásokban egyedi, egymással nem kompatibilis megoldásokkal valósították meg a dinamikus adatbázist. Továbbra is megmaradt azonban az igény a gdf olyan irányú továbbfejlesztésére, hogy a statikus adatbázis mellett a gdf fájl hozzon létre egy szabványos keretet a dinamikus adatbázisok számára is. Ezek az adatbázis keretek, ha feltöltésre kerülnek kiegészíthetik vagy kiválthatják a statikus attribútumokat.
Napjainkra már egész Nyugat Európáról elkészültek a digitális úttérképek. Ezek egyik legnagyobb előállítója a Tele Atlas nevű német cég. Érdekes megjegyezni, hogy a cég Etak nevű leányvállalata az USA egyik legnagyobb úttérkép előállítója.
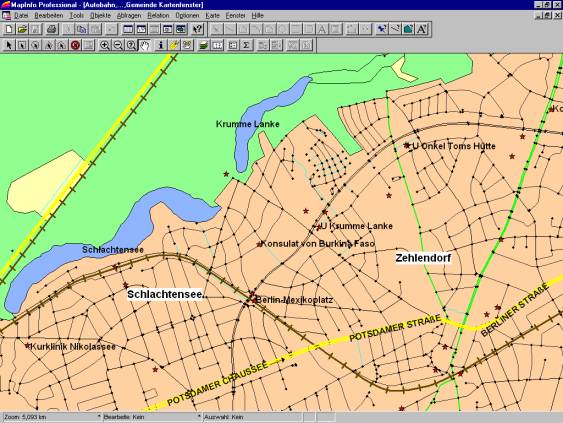
A 6.67 ábrán mutatunk egy németországi gdf úttérkép részletet, a 6.68 ábra pedig a cég két CD alaptípusának külső megjelenését mutatja be. A baloldali CD kizárólag navigációs, illetve az autózáshoz közvetlenül szükséges információkat (pld. szerviz állomások) tartalmazza, míg a jobboldali ezeken kívül még a részletes turista könyv szerepét is képes eljátszani. Megismételjük, hogy akár melyik CD-t is választjuk ezek annak ellenére, hogy a gyártó szerint rendszeresen felújításra kerülnek csak statikus információt tartalmaznak.
|
6.67 ábra - gdf térképrészlet a Mapinfo szoftverben megjelenítve
|
A 6.67 ábrával kapcsolatban érdemes megjegyeznünk, hogy a Mapinfo nem automatikusan fogadja a gdf fájlokat, hanem a megjelenítés előtt azokat konvertálni kell a CITRA gdf olvasóval gdf-ből Mapinfo Tab formátumba.
|
|
6.68 ábra - a Tele Atlas kétféle CD változata
|
Az ITS egyik korai hajtása az AVL-nek rövidített gépjármű helymeghatározás volt. A feladat - a gépjármű helymeghatározása - kétféleképpen is alkalmazható: vagy csak a gépjárműben kerül kijelzésre, vagy valamely diszpécser központban jelennek meg a központhoz tartozó gépjárművek pillanatnyi pozíciói. A feladat legegyszerűbb formában azt jelenti, hogy a vezető előtt lévő képernyőn, illetve a diszpécser képernyőjén, valós időben megjelenik vagy megjelennek a gépjármű(vek) pillanatnyi helyzetét ábrázoló szimbólum(ok), mely(ek) a képernyőre vetített digitális térképen halad(nak).
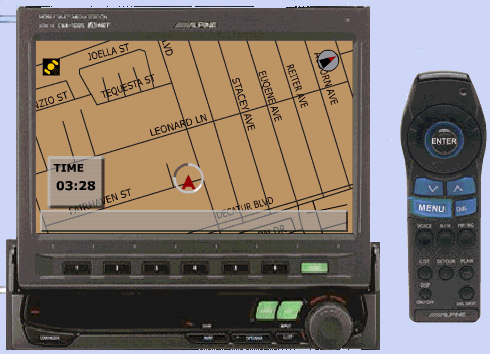
A 6.69 ábrán az ALPINE cég terméke segítségével képzelhetjük el a gépkocsin belüli alkalmazást.
|
6.69 ábra - navigációs képernyő a gépkocsiban
|
Függetlenül attól, hogy magában a gépkocsiban vagy a diszpécser központban akarjuk figyelemmel kísérni a gépkocsi pillanatnyi helyzetét a helymeghatározáshoz ugyanazokat az eszközöket és módszereket használhatjuk. A legfontosabb különbség a két alkalmazás között, hogy az utóbbiban távközlési kapcsolatra is szükség van a gépkocsi és a diszpécser központ között.
Az adatgyűjtéssel kapcsolatban viszonylag részletesen foglalkoztunk a GPS technika általános kérdéseivel, gyakorlati GPS mérési módszerekkel, a földi mobil térképező rendszerekkel, melyek a GPS mérések és az inerciális rendszerek összekapcsolásával képesek a menetközben készített fényképek külső tájékozási adatainak meghatározására. Ez utóbbi alkalmazás azonban utófeldolgozásban határozza meg a szabatos navigációs adatokat ezért változtatás nélkül elvileg sem használható az AVL alkalmazásokban.
Ezen kívül még a következőket is figyelembe kell venni a jelen idejű gépkocsi helymeghatározás egyes részleteiben ismétlésnek tűnő tárgyalásakor:
- az intelligens közlekedési rendszerekben érdekelt szakemberek általában nem érdeklődnek a mobil térképezés részletei iránt;
- a gépkocsi navigációban a pontossági igények alacsonyabbak és más jellegűek, mint a mobil térképező rendszerek esetében;
- a GPS fejezet megírása óta eltelt néhány év jelentős változásokat eredményezett ennek a technikának a fejlődésében;
- ellentétben a mobil térképező rendszerekkel, ahol egy-egy típusból a legjobb esetben is csak néhány darabot gyártanak, a gépkocsi navigációs rendszerek, több tízezres nagyságrendben kerülnek legyártásra.
A jelenidejűségen túl, talán legfontosabb az említett szempontok közül, hogy ellentétben a mobil térképező rendszerekkel a gépkocsi navigáció direkt módon nem igényli a dőlés szögek meghatározását (indirekt módon is csak az azimut vagy irányszög meghatározására lehet szükség), a helyzeti pontosságot pedig csak a használt digitális térképhez kapcsolva lehet úgy meghatározni, hogy keresztirányban a gépkocsit ábrázoló szimbólum legyen rajta az úton, hossz irányban pedig egyértelműen azonosítható legyen, hogy melyik ház (postai cím) előtt halad. Ha figyelembe vesszük, hogy a térkép és a helymeghatározás együttes hibája miatt a jó minőségű rendszerek mindig alkalmazzák a térkép illesztést (map matching), úgy a helymeghatározó eszközök pontosságát elég 10-15 méterben megszabni.
A GPS technika fejlődésében az volt a legfontosabb esemény, hogy Clinton elnök 2000 május 1-ével eltörölte az SA-t (a GPS jelek mesterséges torzítását), ami azt eredményezte, hogy nyugalomban lévő magányos GPS vevőkkel kódfázis méréssel a megadott 10 méternél jóval pontosabb vízszintes meghatározásokat lehet elérni [16]. Mozgó járművön az SA eltávolítása után a GPS pontossága az idő 95%-ában 12 méternél jobb [17]. E technikai hatású politikai döntés mellett a műszaki fejlődés elsősorban abban mutatkozott meg, hogy a GPS vevők mérete és ára jelentősen lecsökkent, pontosságuk pedig megnőtt. A fentiek alapján tehát nyugodtan állíthatjuk, hogy ha a mikrohullámú GPS vételt nem blokkolnák az épületek, fák, stb., illetve, ha a tereptárgyakról történő visszaverődés nem torzítaná a vett jelet, úgy a gépkocsi navigációs célú helymeghatározásához elég volna csak GPS vevővel ellátni a gépkocsikat. Különösen városi környezetben azonban, ahol pedig a navigálásnak sokkal nagyobb a jelentősége mint az autópályán, a GPS jel az útszakasz jelentős részén hiányozhat.
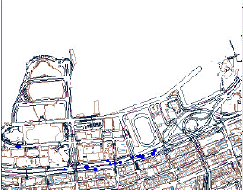
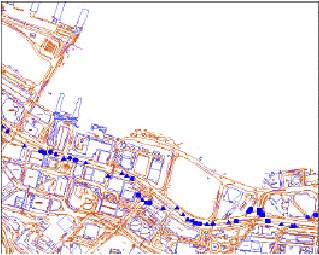
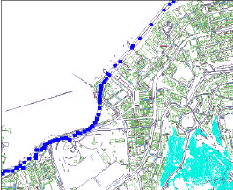
A 6.70 ábrán Hong Kong sűrűn beépített negyedeiben végzett kísérleti eredményeket mutatunk be [18] alapján.
|
|
6.70 ábra GPS jel kimaradások Hong Kong Wan Chai, Központi és Északi negyedeiben (a kék pontokban volt jel, közöttük nem)
|
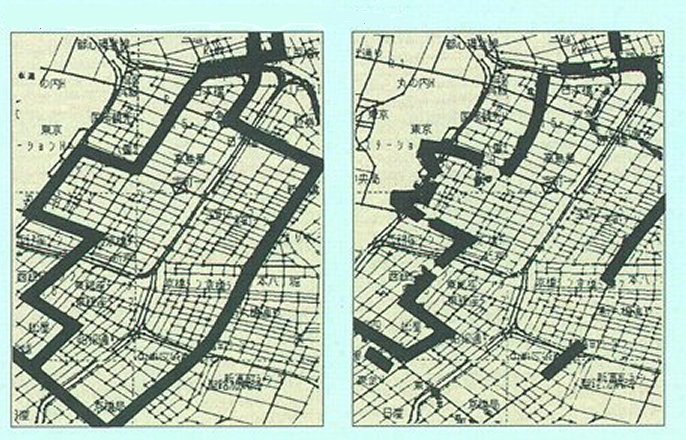
Hasonló eredményeket mutatnak egy japán vizsgálat eredményei, melyeket a 6.71 ábrán láthatunk.
|
6.71 ábra - a baloldali képen a navigáláshoz GPS mellett sebesség szenzort és térkép illesztést is alkalmaztak, míg a jobboldali képen csak GPS-t
|
A két kép egybevetéséből nem csak az tűnik ki, hogy milyen sok helyen szűnik meg teljesen a GPS vétel, de az is hogy milyen nagyok lehettek a torzítások.
Ahhoz tehát, hogy a gépkocsi helyzetét és a hozzá kapcsolódó funkciókat tetszőleges felszínborítás esetén biztosítani lehessen a navigációs rendszerbe kiegészítő szenzorokat és módszereket is integrálni kell. Mivel azonban a GPS modulok ára rohamosan csökken (napjainkban a figyelembe veendő pontossági tartományba eső eszközök 100 dollár értékűek, mely érték 2005-re 50 dollárra fog csökkeni [19]), a kiegészítő szenzorokat sem célszerű a 100000 dolláros tartományban választani. Sajnos az inerciális rendszerek (közös vázra szerelt két vagy három tengelyű gyorsulásmérők és giroszkopok) egyelőre a 100000 dolláros tartományban vannak, bár az úgy nevezett MEMS (Micro-Electro-Mechanical Systems = Mikro Elektromechanikus Rendszerek) technológiával készülő gyorsulásmérő és giroszkóp együttesek a közel jövőben olcsó és megbízható eszközöknek ígérkeznek.
Napjainkban azonban egyelőre a kerék fordulatmérők eredményeinek feldolgozása alapján juthatunk a legolcsóbb megoldásra. A kerék fordulatmérők (odométerek) számtalan fizikai elv alapján készülhetnek. Leggyakrabban optikai vagy mágneses alapon működnek. Zárt rendszerek esetén előnyős az optikai fordulatszám mérők alkalmazása. Ezek úgy működnek, hogy egy osztott kört erősítenek a forgó tengelyre melyre egy az állórészhez kapcsolt fényforrás fényt sugároz. Az osztott kör másik oldalán az álló részhez erősítve egy fotodetektor foglal helyet. Mivel az osztott körön az osztások nem eresztik át a fényt minden alkalommal amikor a fényforrás elé osztás kerül a fotodetektor árama megszakad és a rendszer elektronikája impulzust generál. Az impulzusokat egy számláló számlálja és a felbontási időtől függő idő intervallumokra összegezi. Az ilyen típusú fordulatszámlálókat rendszerint a blokkolásgátló fékrendszerekkel (ABS) összekapcsoltan alakítják ki.
Azokban a gépkocsikban ahol ABS rendszert nem alkalmaznak gyakran külső szerelésű fordulatmérőket alkalmaznak. Ebben az esetben, mivel a szennyeződések zavarják az optikai rendszerek működését rendszerint mágneses megoldáshoz folyamodnak. A kerékre koncentrikusan apró mágneseket szerelnek melyek a kerék elfordulásakor egy mozdulatlanul rögzített tekercs előtt haladnak el. Egy-egy mágnes fluxusa a tekercsben áramot indukál, mely impulzust vált ki az áramkörben.
Ha gépkocsi helyzetét differenciális odometriával akarjuk meghatározni legegyszerűbb, az optikai vagy mágneses fordulatszámlálókat a két hátsó kerékre helyezzük el. Ha ugyanis az első kormányzott kerekekkel akarjuk végezni a pozicionálást, úgy a két fordulatszámlálón kívül még kormány elfordulás mérő szögadóra is szükség van.
Bármelyik műszaki megoldást is alkalmazzuk a hátsó kerekek fordulatmérésére mérési eredményként NJ és NB
jobboldali és baloldali impulzus növekményt nyerünk I időintervallum alatt. Feltételezve hogy az impulzusokat lineáris kerék elmozdulásokká konvertáló tényező
cm = pDn / nCe, ahol
Dn - a nominális kerékátmérő milliméterben,
Ce - az egy körülfordulásra eső impulzusok száma,
n - az áttételi arány a motor és a kerék között (ha a fordulatszám mérő a motorhoz van kapcsolva)
kiszámíthatjuk a baloldali kerék D UB,i illetve a jobboldali kerék D UJ,i útnövekményét:
D UB/J,i = cmNB/J, valamint a hátsó tengely középpontjának elmozdulását D Ui-t az I intervallumban:
D Ui = (D UB,i + D UJ,i) / 2.
Számítsuk ki ez után az I intervallumra eső irányszög változást:
Dqi = (D UJ,i - D UB,i) / b, ahol b a két kerék talaj-érintési pontjának távolsága.
A jármű új relatív( kiinduló irányhoz képesti) irányszöge ezután:
qi = qi-1 + Dqi.
Végül kiszámítjuk a kezdőhelyzethez viszonyított koordináta különbségeket is az alábbi jól ismert képletekkel:
xi = xi-1 + D Uicosqi
yi = yi-1 + D Uisinqi.
A fentiekből világos, hogy elvileg a különbségi kerék-fordulatszám mérésből minden egyéb szenzor nélkül meg tudjuk állapítani a gépkocsi pillanatnyi helyzetét. A módszer eredendő pontossága attól függ, hogy milyen nagy az egy körülfordulásra eső impulzusok száma, és hogy milyen kicsi az idő intervallum. Az eredendő pontosság azonban számtalan hiba következtében erősen lecsökken. A fő hibaforrás a kerekek méretváltozásából és esetenkénti csúszásából adódik. A legnagyobb probléma az, hogy a hibák a haladás során rohamos növekedésnek indulnak mivel a kezdeti szöghibák, hasonlóan a sokszögeléshez a távolsággal arányos koordináta hibákat eredményeznek. E hibák csökkentése érdekében a relatív helymeghatározásban a fordulatszám mérést gyakran csak a távolság mérésére használják az irányszög változásokat pedig száloptikás giroszkóppal mérik.
Az említett elrendezésben a gépkocsi által megtett utat közvetlenül a gépkocsi fordulatszám mérőjéből vezetik ki, mely az átlagolt elfordulás értékekből számított utat adja, az újabb típusú gépkocsikban digitális formában.
Az interferométeres száloptikás giroszkópok
A mobil térképező rendszerekkel kapcsolatban már megismerkedtünk a lézergiroszkópokkal, melyeket széleskörűen használnak az inerciális navigációs rendszerekben. Ezek a berendezések azonban szabatos tükröket, vákuumot és magas feszültséget igényelnek, ami megdrágítja előállításukat és működtetésüket. Természetes, hogy a több száz millió dolláros repülőgépek költségvetése elbírja a néhány százezer dolláros inerciális navigációs rendszereket, az 5000-40000 dolláros autóké azonban már nem. Ezért alkalmaznak az autókban GPS-t, fordulatszámlálót és viszonylag olcsó Interferométeres Száloptikás Gírót (Interferometric Fiber Optic Gyro = IFOG).
A IFOG műszereknek két válfaja van a nyílt hurkú és a zárt hurkú.
A zárt hurkú száloptikás gíró olyan fázis vagy frekvencia visszacsatolással van ellátva, mely kiküszöböli a forgás közben a SAGNAC hatásból eredő fáziseltolást. Mivel azonban ez a rendszer digitális jelfeldolgozást igényel gyártása sokkal költségesebb mint az analóg jelfeldolgozással operáló nyílt hurkú gíróké és ezért nem sorolható be az olcsó kategóriába. Meg kell ugyanakkor jegyeznünk, hogy a mobil térképező rendszerek inerciális rendszereiben egyre elterjedtebben használják, mivel igen kicsiny az idővel arányos torzítása.
A gépkocsi navigáció szempontjából szóba kerülő nyílt hurkú száloptikás gírók ára 1500 $ és 2500 $ között változik napjainkban (2001 április) és mérsékelten csökkenő tendenciát mutat.
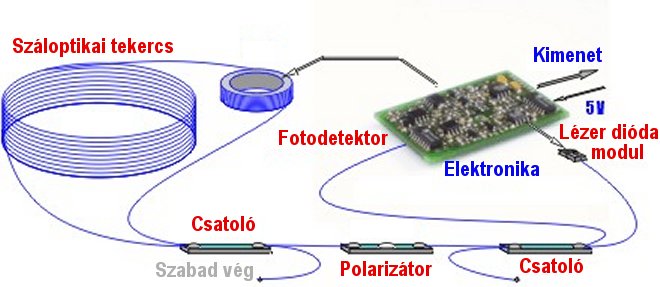
A 6.72 ábrán felvázoljuk a műszer működési elvét a 6.73 ábra pedig egy orosz és egy amerikai gyártmányú száloptikás gíró külső képét mutatja be.
|
6.72 ábra - a nyílt hurkú száloptikás gíró működési vázlata
|

|

|
6.73 ábra - a Fizoptika orosz cég VG 951 (D) típusú digitális kimenetű száloptikás gírója
|
6.74 ábra - a KVH amerikai cég E-Core 2000 FOG típusú digitális kimenetű száloptikás gírója
|
|
A száloptika olyan vékony üveghuzal, mely belső része nco, burkolata pedig ncl törésmutatóval rendelkezik. Mivel a belső rész törésmutatója nagyobb a külső rész törésmutatójánál (nco > ncl) azok a sugarak melyek a huzal tengelyével qc-nél kisebb szöget zárnak be (NA = sinqc = (nco2 - ncl2)½
) a teljes visszaverődés következtében elvileg csillapítás nélkül terjednek végig az üvegvezetéken.
További feltételek az üvegszállal szemben, hogy ne vezessen különböző szög alatt beeső, tehát különböző útakat megtevő sugarakat, azaz, hogy legyen egy módusú, ami a vezeték magjának keresztmetszet csökkentésével érhető el, a mag átmérője meg kell, hogy közelítse a fény hullámhosszát, a másik feltétel pedig, hogy őrizze meg a fény eredeti polaritását, a mag anyagának megfelelő megválasztásával realizálható.
A 6.72 ábra felhasználásával tekintsük át a műszer működési elvét. A szilárdtest lézer fényforrásból a fény az első "csatolóba" lép, majd a polarizátoron keresztül a második "csatolóba" jut. A második csatoló két azonos intenzitású nyalábra bontja a fényt, melyek egymással szemben haladnak a száloptikai tekercsben. A fordított irányban haladó fény átmegy a piezo elektromos modulátoron, mely szinuszosan változó fázismodulációt hoz létre. A tekercsen végighaladva a két fénysugár a második csatolóban egyesül és a létrejött fáziskülönbség függvényében az interferencia vagy erősíti vagy gyöngíti az egyesült fény intenzitását. Az eredő fény a polarizátoron keresztül az első csatolóba jut, mely egy részét a fotodetektorba vezeti, ahol a pillanatnyi fény intenzitás elektromos jellé alakul.
A száloptikai tekercsben létrejövő úgy nevezett Sagnac féle fáziseltolódás - DS = 2pLDW/cl, ahol
L - a vezeték hossza a tekercsben;
D - a tekercs effektív átmérője;
l - a fény közép hullámhossza;
c - a fény sebessége vákuumban;
W - a tekercs tengelye körüli szögsebesség.
Amint látjuk annál nagyobb a fáziseltolódás (tehát a mérési pontosság is) minél nagyobb a tekercs átmérője és a szál hossza. Az első növelésének határt szabnak a műszer beépítési méretei, a másiknak a szálban gyakorlatilag mindég fellépő csillapítás (1 dB/km) és a költségek. A korai rendszerekben néhány km hosszú szálat is alkalmaztak. Manapság már rövidebb szállal is el tudják érni a megkívánt pontosságot, a reciprok folyamban alkalmazott fázismoduláció következtében, a 6.74 ábrán látható műszerben pld. 75 méter hosszú szál van. A fázismodulációnak nem csak az a haszna, hogy jelentősen növeli a fázismérés pontosságát, de az is, hogy lehetővé teszi a baloldali és a jobboldali elfordulások megkülönböztetését.
A szögsebesség szorozva a vizsgált időintervallummal megadja a relatív elfordulást, folyamatosan összegezve a relatív elfordulásokat megkapjuk a kiinduló helyzethez mért irányszög változást.
Lássuk ezek után egy tipikus, jármű navigációs célra gyakran alkalmazott száloptikás giroszkóp, a KVH cég E-Core 1000 típusjelzésű műszerének néhány műszaki adatát:
Műszaki specifikációk
|
Fizikai
|
| Input Feszültség |
12 vagy 24 Volt egyenáram
|
| Fogyasztás | 2 watt (analóg) 3 watt (digitális)
|
| Súly | 0.55 font (0.25 kg)
|
| Méret | 4.3" x 3.5" x 1.6" (109mm x 89mm x 41mm)
|
| Konnektor típus | 15-pines szubminiatűr (DA15P)
|
|
Output
|
| Méretarány tényező
|
20 mV/°/sec
|
| Analóg
|
+2.5 V (zéró forgás) ±2 V, 10 KOhmon
|
| Digitális
|
16 bit, soros, RS232 9600 BPS, 10 érték/sec
|
| Szenzor output (1-es port )
|
analóg, RS232 vagy RS422
|
|
Környezeti
|
| Üzemi hőmérséklet
|
-40°C to +75°C
|
| Tárolási hőmérséklet
|
-50°C to +85°C
|
| Rázás
|
90 G
|
| Elektromágneses és Rádió frekvenciás interferencia
|
CE, IEC 9081-2,3,4
|
| Meghibásodások közötti átlagos idő
|
50,000 óra
|
|
Teljesítmény
|
| Időre vetített torzítás stabilitás
|
2-4 °/óra, 1 szigma
|
| hőmérsékletre vetített torzítás stabilitás
|
0.08 °/sec középhiba, tipikusan 0.4 °/sec, csúcstól csúcsig
|
| Kompenzált torzítás drift
|
5-10°/óra középhiba
|
| Véletlen szöghiba (zaj)
|
20 °/óra/fordulat-Hz, 0.3 °/fordulat-óra
|
| Forgási sebesség
|
±100°/sec
|
| Pillanatnyi sávszélesség
|
100 Hz
|
| Méretarány tényező linearitása
|
kisebb mint 0.5% középhiba (konstans hőmérséklet) kisebb mint 1% középhiba (teljes hőmérsékleti tartomány)
|
| Méretarány tényező hőmérsékleti stabilitása
|
0.5-1.0% középhiba
|
| Bekapcsolási idő
|
1 sec
|
|
6.7 táblázat - a KVH E-Core 1000 típusú száloptikás giroszkóp műszaki adatai
Mikrogépészeti vibrációs (rezgő) giroszkópok
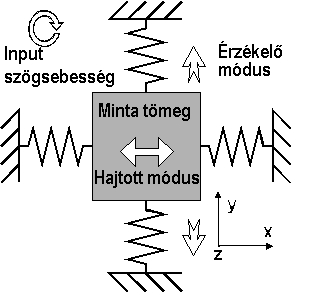
Az előző pontban megismert száloptikás giroszkópok a Sagnac elv alapján műkodnek, a vibrációs giroszkópok a Coriolis erő hatását érzékelik. Amint azt az inerciális rendszerekkel kapcsolatban már megismertük, a "leszíjjazott" forgó mechanikus pörgettyű a forgás okozta Coriolis erő hatására kitér, e kitérés mértékéből lehet következtetni a fellépett szögsebességre. Coriolis erő hatását azonban nem csak a forgó rotor érzékeli, hanem a rezgő (transzlácionális) mozgást végző tömeg is. Ha tehát rugós felfüggesztéssel az x tengely irányú rezgésbe hozzuk a minta tömeget, úgy az válaszként a z tengely körüli forgás hatására fellépő Coriolis gyorsulásra kitér az y tengely irányába. A rendszer működési elvét szemlélteti a 6.75 ábra.
|
6.75 ábra - a vibrációs giroszkóp működési elve
|
Az y tengely irányában létrejövő Coriolis elmozdulás amplitúdója arányos az alaplap elfordulásával. A rendszer dinamikáját a következő egyenlettel írhatjuk le:
aC = 2·vm·w
, ahol
aC - a Coriolis gyorsulás;
vm - a minta-tömeg sebessége;
w - a szögsebesség.
Mivel a minta-tömeg mozgása olyan x irányú rezgés, mely megfelel a tömeg rezonáns frekvenciájának a fenti kifejezés értelmében az y
irányú mozgás is ugyanilyen rezgés lesz, melyet a szögsebesség amplitúdóban modulál. A kapott rezgés hasonlítható a rádióhullámokhoz, ha a vivő hullámnak a rezonáns frekvenciát, a hangnak pedig a Coriolis gyorsulást feleltetjük meg. A rendszer kiegészítő elektronikája demodulálja a rendszerint kapacitás változásból kapott jelet a rezonáns frekvencián és megfelelő jelfeldolgozási technikával a kimeneten az eredeti szögsebességgel arányos feszültséget indukál.
A gyakorlati megvalósítás során lehetőség van több minta tömeg alkalmazására is. E mellett gondoskodni kell a megfelelő felfüggesztésről valamint arról, hogy a jármű egyéb gyorsulásai ne befolyásolják a a Coriolis gyorsulások meghatározását.
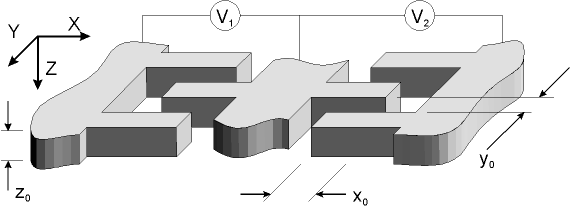
A korai rendszereknél a rezgések generálását fésű fogas elrendezéssel oldották meg. Így például az IMI nevű Berkeley egyetemi kutatócsoport (mely később önállósította magát, még később beolvadt az Analog Devices Inc.nevű
nagyobb cégbe ) a 6.76 ábrán látható elvi elrendezést a 6.77 ábrán látható módon realizálta.
|
6.76 ábra - fésűfogas elrendezésű vibrációs giroszkóp szerkezeti vázlata
|
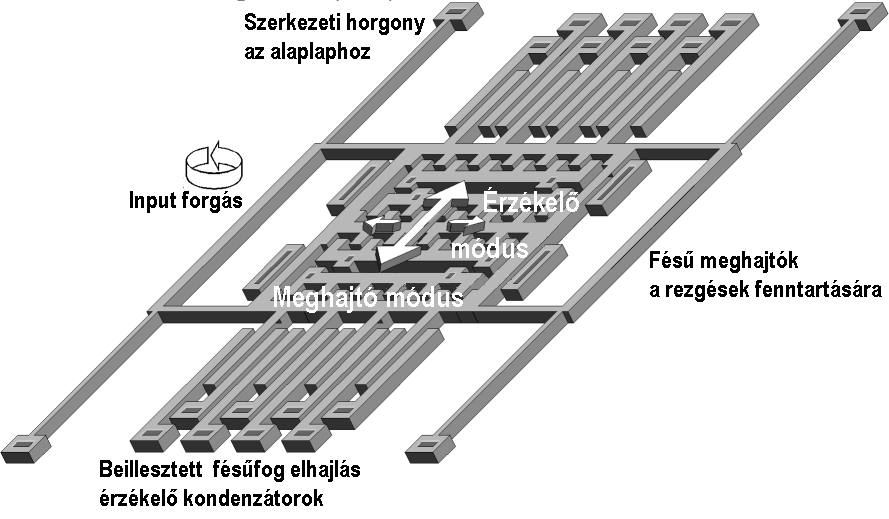
|
6.77 ábra - egy minta-tömegű vibrációs giroszkóp szerkezeti felépítése
|
A rezgéseket az az elektrosztatikus erő gerjeszti, melyet a minta-tömeghez rögzített fésűfogakra illetve az alaplapra szerelt fésűfogakra adott feszültség létrehoz. Az elrendezés előnye hogy jelentős teret biztosít az x tengely menti elmozdulásokra.
Az y irányú elmozdulásokat a fésűfogakra szerelt sík elektródákkal mérik, melyek tulajdonképpen olyan kondenzátorok melyek dielektrikuma levegő. A mozgás következtében az elektródák egymástól mért távolsága megváltozik, ami azt eredményezi, hogy kapacitásuk is megváltozik. A kapacitás változásokat megfelelő híd áramkörben mérik.
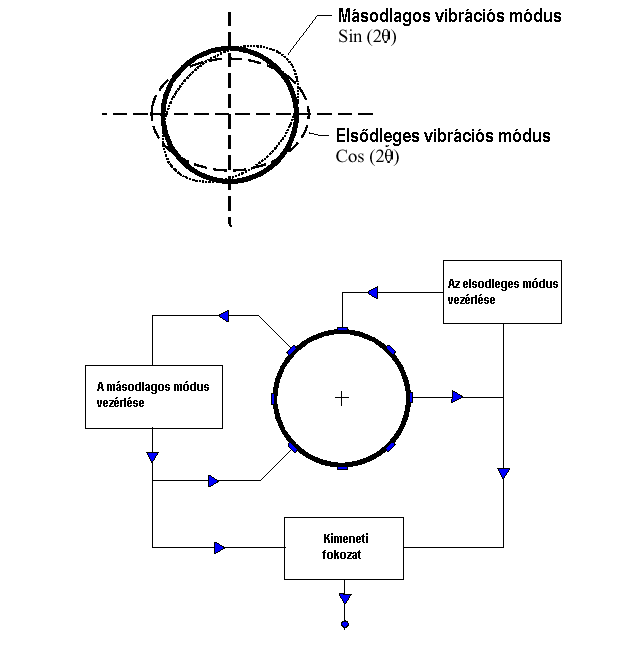
Az utóbbi egy-két évben a fésűfogas vibrációs mikrogépészeti giroszkópokat egyre inkább felváltják a vékony falú gyűrű vagy henger alakú rezgő tömegekkel működő rendszerek. Működési elvük lényegében megegyezik a korábbiakban bemutatottal.
|
6.78 ábra - a hengeres vibrációs giroszkóp rezgési módusai
|
Az elsődleges rezgési módus gerjesztő és érzékelő piezokeramikus elemei páronként a 0° - 180° és 90° - 270° pontokon helyezkednek el, míg a másodlagos rezgés módus piezokeramikus elemei 45°-al eltolva a 45° - 225° és 135° - 315° helyet foglalják el. A piezokeramikus elemeket páronként elektromosan összekapcsolják.
Az elsődleges rezgési módus gerjesztése a 90° - 270° tengely mentén történik a szögsebességet pedig a 0° - 180° tengely elemei érzékelik. A műszer elvileg kizárólag az elsődleges vibrációs módusban is működik: a gerjesztő stabil rezonancia frekvenciával rezgeti a hengert, az érzékelő pedig detektálja a szögsebességgel arányos amplitúdóval modulálva ugyanezt a frekvenciát. Mivel azonban a stabil válaszjel egy rezgési módus esetén csak viszonylag lassan alakul ki (5-10 Hz) ezt a megoldást csak u.n. kis sávszélességű alkalmazások használják. A legtöbb alkalmazás számára az az előnyös, ha a sávszélesség 40 - 50 Hz. Ezt a nagyobb sávszélességet szolgálja a másodlagos rezgési módus aktív vezérlése. A kimeneti fokozat demodulálja a másodlagos módus vezérlő hurkának jelét és a szögsebességgel arányos váltóáramú jellé alakítja (6.78 ábra).
Példaként bemutatjuk a japán Si-VSG típusú mikrogépészeti gyűrű rezonátoros vibrációs giroszkóp külső megjelenését, rezonátorát és műszaki adatait (6.79 ábra, 6.80 ábra és 6.8 táblázat).

|
6.79 ábra - az Si-VSG típusú mikrogépészeti gyűrű rezonátoros vibrációs giroszkóp külső megjelenése
|

|
6.80 ábra - az Si-VSG típusú mikrogépészeti gyűrű rezonátoros vibrációs giroszkóp rezonátora
|
|
| Műszaki Adatok
|
Sebesség tartomány
|
+/- 100 fok/sec
|
Üzemi hőmérsékleti tartomány
|
-40-től +85 C fokig
|
Méretarány tényező
|
20mV/(fok/sec) +/- 0.5%
|
Méretarány tényező hőmérsékleti vándorlása
|
+/- 3%
|
Környezeti torzítási tolerancia
|
+/- 1fok/sec
|
Torzítás hőmérsékleti vándorlása
|
+/- 3fok/sec
|
Torzítás futás közbeni vándorlása
|
0.3 fok/sec
|
Futások közötti torzítás vándorlás
|
0.3 fok/sec
|
Linearitás
|
+/- 0.3% a teljes feszültség tartományra (beszámítva a hiszterézist)
|
Sávszélesség
|
10Hz (-3dB)
|
Bekapcsolási idő
|
0.5 sec max
|
Nyugalmi zaj
|
0.2 fok/sec
|
Zaj vibráció alatt
|
0.1 (fok/sec) /G max
|
Üzemi feszültség
|
5V +/- 250mV egyenáram
|
| Méretek |
35x30x35mm |
|
6.8 táblázat - az Si-VSG típusú mikrogépészeti gyűrű rezonátoros vibrációs giroszkóp műszaki adatai
|
|
A giroszkópok tárgyalása befejezéseképpen meg kell említenünk, hogy már ma is tudnak gyártani olyan igényes vibrációs giroszkópot, mely bizonyos paraméterekben meghaladja a lézergiroszkópok műszaki jellemzőit és alkalmasak inerciális navigációs rendszerben történő alkalmazásra. El-Sheimy szerint [19] még 5 év kell ahhoz, hogy a mikrogépészeti módszerekkel készült érzékelők pontossága és olcsósága elérje azt a szintet, mely lehetővé teszi tömeges alkalmazásukat mozgó helymeghatározó és felmérő rendszerekben.
A Kálmán szűrő
[20]
Kálmán Rudolf a magyar származású amerikai kutató 1960-ban publikálta rekurzív megoldását a diszkrét adatok lineáris szűrési problémájára. Bár a megoldás egyesek szerint N. Wiener 1940-ben publikált szűrője továbbfejlesztésének is tekinthető széleskörű ismertsége és gyakorlati hasznosítása nem csak azzal magyarázható amivel ez utóbbit meghaladta (nem csak skalár mennyiségekre alkalmas, csak az utolsó eredményt kell tárolni, nem az összes megelőzőt), hanem elsősorban azzal a fejlődéssel, mely a mozgó objektumok navigálása terén az utóbbi évtizedben végbement.
Ha egyelőre képletek nélkül, szavakban próbáljuk összefoglalni a szűrő működését, akkor abból kell kiindulnunk, hogy valamely mozgó rendszer állapotát (helyzetét és sebességét) szeretnénk meghatározni a rendszer mozgását leíró szabály és bizonyos időpontokban végrehajtott mérések segítségével. Az eredeti Kálmán szűrő alkalmazása esetén feltételezzük, hogy a mozgást leíró differenciál egyenlet lineáris. Feltételezzük továbbá azt is, hogy az a függvény kapcsolat, mely segítségével a mért mennyiségekből a helyzetet meghatározó koordináták számíthatók szintén lineáris. Rögtön megjegyezzük hogy az általunk vizsgált esetekben ezek a feltételek sohasem teljesülnek, ezért esetünkben az úgynevezett Kiterjesztett Kálmán Szűrőt alkalmazzuk, mely pontonként linearizált pálya és megfigyelési egyenletekkel vezeti vissza a problémát az eredeti lineáris alapokra. További feltételezésünk, hogy mind a mozgás, mind a mérés egymástől független, zérus középértékű, normális eloszlású hibával, úgy nevezett fehér zajjal terhelt. A hibákat, illetve az azokat jellemző variancia-kovariancia mátrixokat a rekurzió megkezdése előtt kísérletek alapján lehet megbecsülni.
A rekurzív szűrő, mint már utaltunk rá, egy meglévő helyzet becsléséből kiszámítja a következő helyzet becslését és figyelembe véve az itt (a következő helyzetben) fellépő mérési eredményt véglegesíti a becslést. Ezen kívül megbecsüli a koviarianciát, majd a mérés felhasználásával véglegesíti a kovariancia becslést. A működés tehát két fázisú: az első fázis "jósol", a második fázis "korrigál".
A leírtak arra az esetre igazak amikor jelenidejűleg akarjuk meghatározni a mozgó objektum helyzetét, azaz ha az időben előre lépegetünk. Más a helyzet akkor, ha mint például a mobil térképezésben, utófeldolgozással határozzuk meg a felvételi pontok koordinátáit. Ilyenkor a szűrőt nem csak előre, de visszafelé is futtatjuk, amivel elérjük azt, hogy a későbbi mérési eredményekre támaszkodva javítani tudjuk a korábbi becslések eredményeit. Az előre alkalmazott futást szűrésnek, az idővel ellentétes irányú futást simításnak hívjuk.
Ezek után, levezetések nélkül, megpróbálkozunk a vázolt folyamatok matematikai leírásával is, a HTML által adott környezet lehetőségein belül.
A diszkrét, idő-függő folyamat állapotát az alábbi lineáris differencia egyenlettel írjuk le:
xk = Axk-1 + Buk + wk-1, (1)
ahol:
k - a diszkrét időpillanatok indexe;
x - az n dimenziós állapot vektor;
w - a haladási modellt terhelő zaj, melyet a Q variancia-kovariancia mátrix ír le;
A - az az n x n-es mátrix, mely az előző állapotra vonatkoztatja a jelenlegi állapotot ha nincs meghajtó függvény és modell zaj;
B - n x l-es mátrix a lehetséges uk vezérlő inputot rendeli az x állapothoz.
A zk méréseket az állapothoz a következő egyenlet kapcsolja:
zk = Hxk + vk, (2)
ahol
H - a mérések és állapot kapcsolatát leíró m x n mátrix;
vk - a méréseket terhelő hiba, melyet az R variancia-kovariancia mátrix ír le.
| Jelölje az állapot vektor k időpillanatra vonatkozó előzetes - a priori becslését |
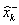
|
, |
| ugyanennek utólagos - a posteriori becslését pedig
|
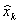 | . |
A bevezetett becslés értékek felhasználásával meghatározhatjuk a becslés előzetes - a priori és utólagos - a posteriori hibáját:
Mivel a variancia-kovariancia mátrix a hibák négyzetének várható értékeként határozható meg, felírhatjuk mind az a priori mind az a posteriori állapot becslés variancia-kovariancia mátrixát az alábbiak szerint:
Pk- = E[ek- ek- T], (3)
Pk = E[ek ekT]. (4)
Célunk - a k időponti utólagos állapot becslés a következő kifejezés alapján határozható meg:
Az (5) egyenlet jobboldalán található zárójeles kifejezés az úgynevezett innováció mutatja, hogy mennyire különbözik az előzetes becslés a mérési eredménytől. Az n x m dimenziójú K mátrix az úgynevezett nyereség vagy keverési faktor abból a feltételből kerül meghatározásra, hogy minimalizálja a (4) a posteriori hiba kovarianciát:
Kk = Pk-HT(HPk-HT + R)-1 (6)
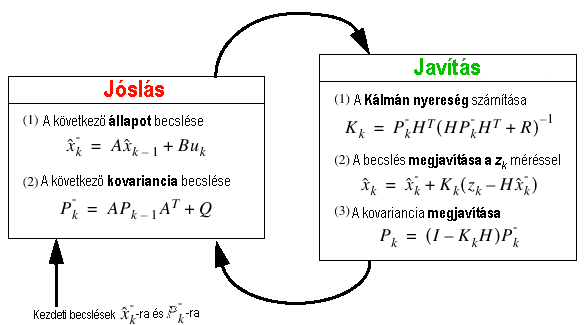
Ezek után felvázolhatjuk a szűrő kétlépcsős működését minden k időpontban.
Az első lépésben a szűrő elvégzi a jóslást az előző időpillanat állapot és kovariancia értékei alapján:
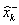
|
=
|
A
|
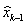
|
+ Buk (7)
|
Pk- = APk-1AT +Q. (8)
A (7) egyenletben szereplő A és B együttható mátrixok a mozgás modelljéből származnak és az (1) egyenlet kapcsán már megismertük őket. A (8) egyenletben szereplő Q variancia kovariancia mátrix a dinamikus modell véletlen hibáiból ered, melyet a futás előtt meg kellett becsülnünk, a (4) szerinti P variancia-kovariancia mátrix pedig az induláskor felvett kezdeti értékére támaszkodva a (8) illetve (11) kifejezésekből folyamatosan számolható.
A második lépésben a szűrő megjavítja a jóslási eredményeket az alábbiak szerint:
Kk = Pk-HT(HPk-HT + R)-1 (9)Pk = (I - KkH)Pk- (11)
A javítási szakasz első feladata az úgynevezett Kálmán nyereség számítása a (9) kifejezés alapján (ugyan ezt az egyenletet felírtuk korábban is (6) itt csak a teljesség kedvéért ismételtük meg). A következő lépésben a friss mérési eredmény bevonásával végezzük el az állapotbecslést a (10) kifejezés felhasználásával, amit szintén megismételtünk, korábbi száma az (5) volt. Utolsó lépésben elvégezzük az utólagos hiba kovariancia becslést a (11) segítségével.
Az R variancia-kovariancia mátrixot a mérőeszközzel végzett próbamérésekből a szűrő használata előtt "off-line" szokták meghatározni. A Q mátrixot a mozgási modell kifejezését már nehezebb meghatározni. Alapszabály, hogy minél egyszerűbb a mozgási modell, annál nagyobb hibákat kell megengedni a Q mátrix felépítésekor. A lineáris szűrő kétütemű működését a 6.81 ábrán foglaljuk össze.
|
6.81 ábra - a Kálmán szűrő működési ütemei
|
Ha a mozgás állapotot leíró differencia egyenlet nem lineáris, úgy a mozgás állapotot az (1) helyett a következő kifejezéssel írhatjuk le:
xk = f(xk-1, uk, wk-1), (12)
hasonlóképpen a mérések és az állapot kapcsolatát leíró egyenlet nemlineáris esetben a (2) helyett a következő alakot veszi fel:zk = h(xk, vk), (13)
ahol f illetve h nemlineáris függvények.
Ebben az esetben a Kiterjesztett Kálmán Szűrőt használhatjuk, amely az egyes becslési pontok szerint linearizálja a nemlineáris egyenleteket. Tulajdonképpen arról van szó, hogy a kérdéses egyenleteket a becslési pontokban Taylor sorba fejtjük és az egynél magasabb kitevőjű tagokat elhagyjuk. Természetesen a (12)-ben lévő wk-1, illetve a (13)-ban lévő vk hibát nem tudjuk az egyes időpontokra megadni, ezért a sorbafejtéshez szükséges pont becsléseknél értéküket zérusnak választjuk:
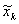
|
= f(
|
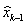
|
, uk, 0) (14)
|
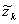
|
= h(
|
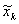
|
, 0). (15)
|
A (14) és (15) kifejezésekkel meghatározott pontokban linearizálva a (12) és (13) kifejezéseket a következő egyenleteket kapjuk:
| xk ≈
|
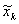
|
+ A(xk-1 -
|
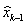
|
) + Wwk-1, (16)
|
| zk ≈
|
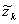
|
+ H(xk -
|
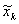
|
) + Vvk. (17)
|
A (16)-ban és (17)-ben szereplő együttható mátrixok nem mások mint a nem lineáris f illetve h függvény parciális deriváltjai a (14) illetve (15) kifejezés által meghatározott helyeken. Irjuk fel a négy mátrix i,j elemeinek képzési szabályait:
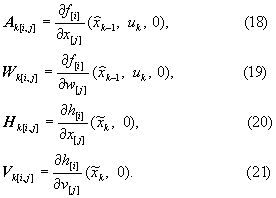
Ezek után felírhatjuk a két lépcsős algoritmust a (7)-(8) illetve (9)-(11) képletek analógiájára a nemlineáris esetre is:
Az első lépésben a szűrő elvégzi a jóslást az előző időpillanat állapot és kovariancia értékei alapján:
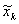
|
= f(
|
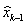
|
, uk, 0) (22)
|
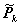
|
= AkPk-1AkT
| + WkQk-1
| WkT. (23)
|
Összehasonlítva a (7) kifejezést a (22)-vel a következő különbségeket látjuk a lineáris és nem lineáris eset között a következő állapot jóslásában:
- a két eset könnyebb megkülönböztetése érdekében a következő állapot jóslását nem lineáris esetben felső hullámvonással jelöltük a jobb felső "-" index helyett;
- az előző időpontra vonatkozó becslést illetve az aktuális időpontra vonatkozó vezérlő inputot az f függvénybe kell behelyettesíteni.
A kovariancia jóslást végző (8) és (23) kifejezések között a következő különbségekre figyelhetünk fel:
- a nem lineáris eset megkülönböztetésére a kovariancia jóslásnál is hullámos vonalat használunk;
- a nem lineáris esetben az A mátrix minden k időpontra a (18) szerint újra számítandó;
- a nem linearitás következtében a Q variancia-kovariancia mátrixot transzformálni kell a minden k időpontra a (19) szerint számítandó W mátrixszal;
- a Q mátrix indexálásával azt jelöltük, hogy a különböző időpillanatokra különböző modell hiba használható (ez elvileg a lineáris esetben is lehetséges, de ott kevéssé indokolt).
A második lépésben a szűrő megjavítja a jóslási eredményeket az alábbiak szerint:
| Kk =
|
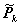
|
HkT(Hk
|
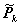
|
HkT + VkRkVkT)-1, (24)
|
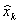
|
=
|
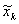
|
+ Kk(zk - h(
|
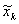
|
, 0)), (25)
|
| Pk = (I - KkHk)
|
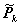
| . (26)
|
A korrekciós képletekben a nemlineáris eset a következőkben tér el az eredeti, lineáris esetre vonatkozó javításoktól:
- a kovariancia jóslását a (24)-ben és (26)-ban ellentétben a (9) és (11)-el nem jobb felső "-" indexszel, hanem hullámos felülvonással jelöltük;
- szintén hullámos felülvonást használtunk (25)-ben az állapot jóslásra a (10) jobb felső "-" indexe helyett;
- a (24)-ben és (26)-ban szereplő H mátrixot minden k időpillanatra újra kell számolni a (20) kifejezés felhasználásával;
- a (24)-ben szereplő R mérési hiba variancia-kovariancia mátrix értéke időpillanatonként változtatható, és a Kálmán nyereség kiszámításához transzformálandó a (21) kifejezésből minden k pillanatra számítandó V mátrixszal;
- a (25)-ben a nem lineáris h függvényt kell használni.
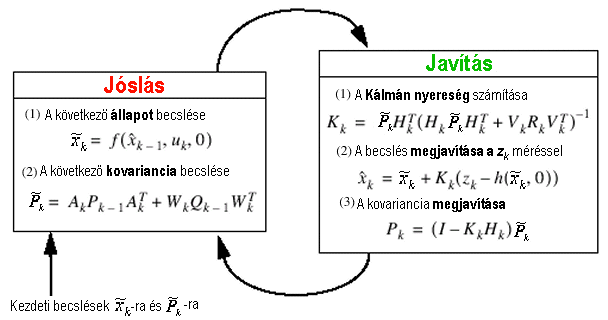
Végül foglaljuk össze a 6.82 ábrán a kétlépcsős becslési folyamatot a Kiterjesztett Kálmán Szűrő esetére.
|
6.82 ábra - a Kiterjesztett Kálmán Szűrő működési ütemei
|
A szenzor integrációt a szűrővel többféleképpen lehet modellezni. A [21] a differenciális GPS és az odométerből és giroszkópból álló DR rendszer integrálásához a következő állapotegyenlet használja:
xk = Axk-1 + wk-1, (27)
ahol x = [x, y, vx, vy, dtu, dtru, e, B].
Az állapot vektor tehát tartalmazza a helyzetet megadó x, y koordinátákon kívül az x és y írányú sebességkomponenseket (vx, vy), a műkold vevő órahibáját (dtu), a vevő órahiba változását (dtru), a giroszkóp vándorlási (elállítódási) sebességét (e) és a fordulatszámláló méretarány hibáját (B). Az A együttható mátrixot a következőképpen választották meg a modellben:
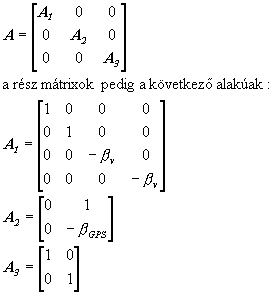
ahol a bv
és bGPS
a sebesség és az órahiba idővel való változását jellemző tényezők.
A (13) mérési egyenletben szereplő nem lineáris kapcsolat a mérések tárgya és az állapotváltozók között:
h(x) = Ri + dtu. (28)
Az Ri (28)-ban az i-ik műhold és az álláspont hibátlan távolságát jelenti. Ahhoz tehát, hogy a következő lépésben elkészíthessük a Hki Jacobi mátrixokat mind a 4 műholdra fel kell írnunk az állapot vektorral kifejezve a kérdéses távolságokat. A továbbiakban a megoldást a 6.82 ábra képletei szolgáltatják, csak nem szabad elfelejtenünk, hogy minden időponthoz n (a hivatkozott előadás esetében 4) távolság mérés tartozik.
Inerciális rendszerek és GPS integrálása esetén az állapotegyenlet rendszerint az inerciális rendszer és a GPS szolgáltatta koordináták különbségére vonatkozik. Például a [22] kandidátusi disszertáció téziseiben az állapotegyenlet:
dxk = dxk-1 + dvk-1t, (29)ahol dx az inerciális és GPS koordináták különbsége (az inerciális koordináták hibája), dv pedig az inerciális és GPS sebességek különbsége (az inerciális sebességek hibája), t - az idő.
A mérési egyenlet szintén lineáris, mivel
zk = dxk + vk, (30) ahol vk = -dxGPS - a GPS mérés hibája.
A Kálmán szűrő felírásakor a szerző az A alakmátrixot az egységgel teszi egyenlővé és az e miatt létrejött modell hibát a Q mátrix felírásában veszi figyelembe. Az, hogy az alakmátrix egység mátrix azzal a következménnyel is jár, hogy az állapot k pillanatnyi jóslása ((7) képlet) megegyezik a k-1 pillanatra vonatkozó becsléssel, azaz az ismertetett modell k pillanatra vonatkozó becslése (az (5) képlet alkalmazva esetünkre) a következő alakban írható fel:
A k időpillanatra jósolt variancia kovariancia mátrix (8) a vizsgált modell esetében az alábbi lesz:
Pk- = Pk-1 + 3Q, (32)
ahol
| Q = E[dv2]t2 ≈ E[
|
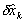
|
dvkt].
|
A hivatkozott tézisekből nem igazán világos, hogy a "3" szorzó milyen meggondolásokból került a (32)-be. A Q meghatározásához csak annyi kommentárt fűz a szerző. hogy az utolsó 200 másodperc koordináta becsléseiből határozható meg.
A mérési hiba a H mátrix egységnyi felvételével
| vk = zk -
|
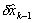
| . (33)
|
Rk a mérési hibák variancia-kovariancia mátrixa ezek után a következő kifejezésből számítható:Rk = vk2 - Pk-. (34)
A Kálmán nyereség (lsd. (9)) esetünkben a következő alakra egyszerűsödik:
Kk = Pk-(Pk- + Rk)-1, (35)végül pedig a modell variancia-kovariancia mátrixának becslése a k pillanatban (11) a következő képlettel fejezhető ki:Pk = (1 - Kk)Pk-. (36)
Bár az INS és GPS összekapcsolása a navigációban elsősorban azt a célt szolgálja, hogy ott is megbízható koordinátákat kapjunk, ahol a műholdakra nincs rálátás (a mobil térképezésnél természetesen a külső tájékozás szögértékei legalább ilyen fontosak), a 20 -30 másodperc hosszúságú hosszabb GPS kimaradások azt eredményeznék az ismertetett modellnél, hogy az inerciális rendszer elkúszása jelentősen lerontaná a becslési eredményeket. Ezt elkerülendő a szerző olyan skaláris adaptív algoritmust dolgozott ki, mely javítja az INS értékeket és ezzel egyszersmind javítja a közbenső pontok becslését. A nagyobb periódus értékek megválasztásánál az Inerciális Navigációs Rendszer hibaegyenleteinek analitikus megoldását alkalmazza a szerző. Sajnos ezekről a kérdésekről több részlet a hivatkozott műben nem található.
Reméljük, hogy a két bemutatott példa megfelelően illusztrálja, hogy a Kálmán szűrő többféleképpen is megtervezhető a konkrét rendszer tanulmányozása alapján és hogy a hiba mátrixok helyes megválasztása csak kitartó előzetes kísérletek alapján érhető el.
A Térkép Illesztés (Map Matching)
Az előző pontban vázolt, és még egyéb módszerekkel is bővíthető gépkocsi navigációs rendszerek által meghatározott koordináták nem feltétlenül esnek egybe a digitális térképen ábrázolt utakkal. Ez részben a helymeghatározás, részben a térkép hibáival magyarázható. A gépkocsi vezetője ugyanakkor jogosan azt várja, hogy a gépjárművét jelző szimbólum a kérdéses út képén haladjon a képernyőn. Még fontosabb, hogy a különböző útvonal kijelölő algoritmusok olyan álláspontokat igényelnek kiinduló információként, melyek egybeesnek valamely út vagy utca nyomvonalával. A térkép illesztő algoritmusok lényege, hogy geometriai, valószínűségi vagy logikai feltételezések alapján kijelölik azt a helyet a nyomvonalon (azokat a koordinátákat), melyet a navigációs rendszer akkor szolgáltatna, ha sem a helymeghatározás sem a térkép nem tartalmazna hibákat.
Az elmondottakból világos, hogy a térképillesztést csak akkor lehet alkalmazni, ha a járművek utakon és utcákon (tehát tulajdonképpen kényszerpályán) haladnak. A terepi navigációban (katonai, földmérési, mezőgazdasági, erdészeti, geológiai, építési, stb. feladatok megoldásakor) a térkép illesztő modult ki kell kapcsolni.
Tárgyalásunkban először a térkép illesztés általános kérdéseit vázoljuk fel, a további részletek iránt érdeklődőknek javasoljuk a [23] és [25] tanulmányokat, majd összefoglaljuk a [24]-ben leírt ausztrál eset tanulmányt.
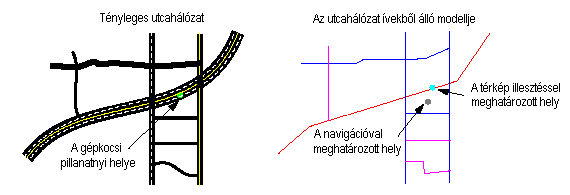
A 6.83 ábrán feltüntettük a megoldandó feladatot: a gépkocsi valahol az utcahálózaton mozog. A mérési hibák valamint az utcahálózat digitális modelljének hibái következtében a pillanatnyi álláspont koordinátái nincsenek rajta a kérdéses utcát modellező íven (a továbbiakban is feltételezzük, hogy az utcahálózatot tengelyvonalával topológiai, ív - csomópont hálózatra képeztük le).
|
6.83 ábra - a térkép illesztési feladat illusztrációja
|
Tételezzük fel, hogy valamely t időpontra a gépkocsi tényleges Pt
helyzetét Pt értékkel becsüljük (mérjük), úgy a térképillesztés feladata, hogy
- megtaláljuk azt az A ívet, az utcahálózat leképezésében, melyre Pt illeszkedik;
- megfeleltessük a megtalált A ívet annak az A utcának, melyet reprezentál;
- megkeressük, hogy az A íven belül melyik helyzet felel meg legjobban Pt-nek.
A számtalan térkép illesztési algoritmus közül a legegyszerűbb a "pont a ponthoz" módszer. Ebben az esetben először megkeressük azokat a csomópontokat és töréspontokat, melyek a pont becsült helyzetétől számítva egy megadott távolságon belül helyezkednek el (a távolságot a navigációs hiba 2-3-szoros értékében szokás felvenni). Ezután Pytagoras tételével kiszámítjuk a becsült álláspont és a kiválasztott csomó- és töréspontok távolságát és az álláspontot abba a térképi pontba toljuk, melynek a távolsága a becsült helytől a legkisebb. A módszer komoly hiányossága, hogy azokban az esetekben amikor hosszú egyenes szakaszokon haladunk, melyeken nincs töréspont, másik ívhez tolja az álláspontot mivel a másik ív töréspontja közelebb van mint a saját egyenes szakasz végét kijelölő távoli pont.
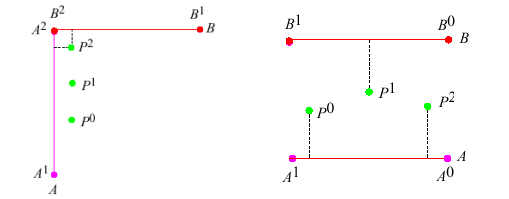
Valamivel megbízhatóbb eredményeket kaphatunk a "pont a görbéhez" illesztés alkalmazása esetén. Mint ismeretes az ívek egyenes szakaszokból állnak. Valamely egyenes szakasz és a pont távolságát vagy a pontból az egyenesre bocsátott merőleges határozza meg, ha talppontja a szakaszon belül van, vagy a pont és az egyenes egyik végpontjának távolsága, ha a talppont a szakaszon kívül van. A feladat tehát az, hogy először kijelölünk egy keresési tartományt, megkeressük a pont távolságát valamennyi a tartományba eső egyenes szakasztól és a legrövidebb távolságra eső szakaszra (talppontra vagy végpontra) helyezzük a pontot. Bár ez a módszer első látásra tökéletesnek tűnik, több hátránya is van.
|
6.84 ábra - a pont a görbéhez illesztés két hibalehetősége
|
Amint a 6.84 ábra baloldali részén bemutattuk, mivel a módszernek nincs emlékezete ezért a p2 pontot csak akkor illeszti helyesen az A ívre, ha a pont merőleges távolsága az A-tól kisebb mint a B-től, ellenkező esetben, hibásan a p2 a B ívre kerül. Szintén hibát eredményezhet az ábra jobb oldalán bemutatott eset is, amikor a pontok nagyjából az A és B ívek közti távolság felében helyezkednek el és az, hogy melyik ívre illeszkednek csak egy hajszálnyi távolság változástól függ.
A tisztán geometriai alapú térkép illesztés legkomplikáltabb válfajában vonalakat illesztenek vonalakhoz. A mérések által meghatározott vonalat ahhoz a hálózati vonalhoz illesztik, melyektől mért átlagos távolsága minimális. Ennél bonyolultabb és főleg nem városi utakon alkalmazott módszer, amikor a vonalak görbülete alapján hajtják végre az illesztést.
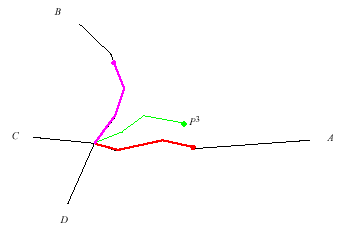
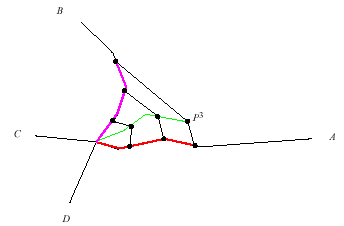
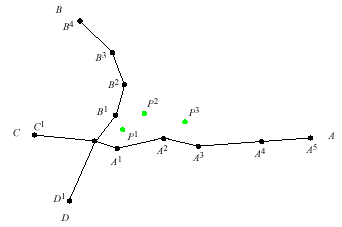
Döntő javulást eredményezhet bármely felvázolt algoritmusban a topológiai információ ismerete. Ez esetünkben azt jelenti, hogy ismerjük a kiinduló csomópontot és a belőle kiinduló íveket. Ezt az információt úgy vesszük figyelembe, hogy az első illesztésre csak azok az ívek jelölhetők ki, melyek a kezdő csomópontból indulnak. Hogy miként működik a tide algoritmusa vonal vonalhoz illesztése esetén [23] a 6.85 ábrán mutatjuk be:
|
|
|
6.85 ábra - vonal vonalhoz illesztése a topológia (kiinduló adatok) figyelembevételével
|
Esetünkben a kiindulópont az A, B, C és D ívek metszéspontja volt. az algoritmus első lépésben egyenesekkel köti össze a kezdőpontot a P1, P2 és P3 pontokat majd meghatározza a kezdőpontból kiinduló valamennyi íven (az ábrán csak az A és B ív van kiszínezve) az észlelési vonallal azonos hosszúságú szakaszokat. A következő lépésben egyenlő részekre osztja (az ábrán három részre) valamennyi egyenlő hosszúságú szakaszt. Ezután az észlelési vonal szakasz végpontjait összeköti az A, B, C és D íveken létrehozott szakaszok végpontjaival és kiszámolja, hogy melyik ívre vonatkozó távolságok összege minimális. Erre az ívre fogja áthelyezni az észlelési vonalat. az ábra esetében ez az ív az A.
Nagyon érdekes esettanulmányról számolt be a közelmúltban egy ausztrál szerzői kollektíva [24]. A projekt keretében olyan hardver szoftver együttest állítottak össze, mely sikeresen oldotta meg a gépkocsi navigációt Melbourne sűrűn beépített részein is.
A hardver egy olcsó, Garmin GPS 45 típusú GPS vevőből, KVH E-Core 1000 FOG típusú száloptikás gíróból, a gépkocsi fordulatszámlálójából és egy Pentium 133 laptop számítógépből állt.
A szoftver alapját a Smallworld GIS képezte (ez tartalmazta az utcahálózatot), melyet részben saját, MAGIK nevű objektum-orientált program nyelvén, részben MS Visual Basicben programoztak. Ez utóbbit azért alkalmazták, mivel gazdag soros átviteli könyvtárakkal rendelkezik, melyek megkönnyítették a programozást. Az elkészített szoftver biztosította a navigációs megoldást mely főként a fordulatszámlálóra, gíróra és térkép illesztésre támaszkodott. A külön üzemmódban működtetett GPS-t csak akkor vonták be a navigációba, ha eltérése az alaprendszertől nem haladta meg a ±(12m + a az utolsó GPS mérés óta megtett út 2%-a) értéket.
A térkép illesztés négy kritériumon alapult:
- a legközelebbi út, ami tulajdonképpen a korábbiakban tárgyalt térképillesztést jelenti. Ez a kritérium azonban nem működik megbízhatóan kereszteződésekben, illetve, ha az utcák túl közel esnek egymáshoz. A probléma csökkentésére szolgál
- az irányszög illesztés, azaz a legközelebbi utat csak akkor kell kiválasztani, ha az irányszöge is megegyezik a haladás irányszögével. Ez a feltétel egyben elősegíti, hogy a fordulókon megnövekvő hosszmérési hibák a fordulók után kiküszöbölődjenek.
- Bizonyos esetekben figyelembe kell venni az elérési lehetőséget is. Ez azt jelenti, hogy meg kell vizsgálni, hogy járt-e a jármű a régi útját az újjal összekötő utcán, mert ha nem, akkor nem illeszthető az új utcára.
- Az utolsó feltétel a hosszmérési hibák további redukálását szolgálja oly módon, hogy a hosszakat minden ív megtétele után a térképből számolja és ezzel megjavítja a fordulatszámláló nyújtotta eredményt.
A számtalan kísérleti eredmény azt bizonyította, hogy a módszer legalább is a teszt-területen maradéktalanul teljesítette az elvárásokat. Külön érdekessége a kutatásnak, hogy kísérletileg is igazolta, hogy nagyvárosi körülmények között nem csak a GPS kiesése okoz problémát, de a GPS hibák is: azokban a kísérletekben ahol figyelembe vették a GPS-t akkor is ha eltérése az alaprendszertől nagyobb volt mint a tolerancia, nem kaptak folyamatos, utcákra feszített navigációt.
A Mobil Telefon Rendszerek Lehetőségei a Navigáció Finomításában
A mobil telefonhálózatok egyre nagyobb szerepet kaphatnak a helymeghatározásban [18], [26]. Az Egyesült Államok Föderális Távközlési Bizottsága (U.S. FCC) előírásai szerint például a 2001 október 1 után forgalmazott új mobil telefonok 50%-a, a 2002 október 1 után forgalmazottaknak pedig legalább 95%, 2004-ig pedig 100%-a kell hogy rendelkezzen helymeghatározó szolgáltatással.
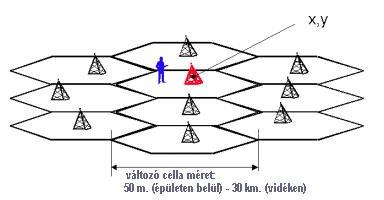
A legegyszerűbb helymeghatározás a kezdő cella azonosítása alapján történik, mely minden mobil telefon rendszer szerves része. A helymeghatározás pontosságát ebben az esetben annak a cellának a területe határozza meg, melyben a hívás történt. Ez az érték városi környezetben egészen 50 m.-ig csökkenhet, szabad területen viszont elérheti a 30 km-t is (6.86 ábra).
|
6.86 ábra - helymeghatározás a cella azonosító alapján
|
Ezért a pontosabb helymegadás érdekében (melyet eredetileg a vészhívások helyhez kötési igénye váltott ki) olyan módszereket dolgoztak ki, melyek vagy a hálózat, vagy a mobil egység vagy mindkettő módosítását igénylik. Az Európai Távközlési Szabvány Intézet (ETSI) és az Amerikai Nemzeti Szabvány Intézet (ANSI) a kezdő cella azonosításon túlmenően a következő módszerek szabványosítását határozta el:
- GPS-szel Támogatott (A-GPS);
- Javított Időkülönbség Mérés (E-OTD);
- Érkezési Idő (ToA).
A GPS-szel támogatott telefonok tulajdonképpen egy GPS vevőt szerelnek be a mobil telefonba. Mivel azonban éppen a GPS kihagyásai és hibái miatt igyekszünk bővíteni a helymeghatározó módszereket ez a megoldás a navigáció megjavítása szempontjából érdeklődésre nem tarthat igényt.
A Javított Időkülönbség Mérés (E-OTD) alapvetően csak a hálózati állomások módosítását igényli, a korszerű mobil egységekben csak a szoftvert kell megváltoztatni.
A módszer azon alapul, hogy megméri a Bázis AdóVevő Állomásból kibocsátott jel érkezési idő különbségét a Mobil telefon és egy ismert földrajzi helyzetű Referencia Állomás között (azaz hogy milyen időkülönbség van a jel vételi pillanatai között a két említett helyen). A mobil telefon helyzete akkor határozható meg, ha a fenti mérés három földrajzilag különböző Bázis AdóVevő Állomásról kerül végrehajtásra.
A futási időket a Mobil Telefon és a Referencia Állomás órái mérik. Mivel a Mobil Telefon órája nincs szinkronizálva a Referencia Állomás órájához, ezért a mobil órahibája is ismeretlenként fog jelentkezni az egyenletekben. Az összes eredmény birtokában a földrajzi helyzetet vagy a hálózat számítja, vagy megfelelő szoftver birtokában a Mobil Telefon. Ez utóbbi esetben azonban az összes máshol mért adatot valamint a referencia pontok koordinátáit SMS üzenetben meg kell küldeni a Mobil Telefonnak. Ha a Mobil Telefon időmérését tM-el, a Referencia Állomás időmérését pedig tR-el jelöljük, továbbá dMB a Mobil Telefon és a Bázis Állomás távolsága, dBR a Bázis Állomás és a Referencia Állomás távolsága, c a rádióhullámok terjedési sebessége, e a mobil órahibája, akkor az egy mérésre vonatkozó egyenlet
dMB - dBR = c(tM - tR + e). (37)
Mivel a (36)-ban dBR a Referencia Állomás és az aktuális Bázis Állomás koordinátáiból számítható, a Bi Bázis Állomáson végrehajtott jelkibocsátás eredményeképpen felírható, hogy a Mobil Állomás egy olyan körön kell, hogy elhelyezkedjen, melynek középpontja Bi, egyenlete pedig:
(xM - xBi)2 + (yM - yBi)2 = (c(tM - tR + e) -dBiR)2. (38)
Amint már említettük, a meghatározandó 3 ismeretlenhez (xM, yM, e) három (38) típusú egyenletet lehet felírni. A feladat geometriai értelmezését a 6.87 ábrán mutatjuk be.
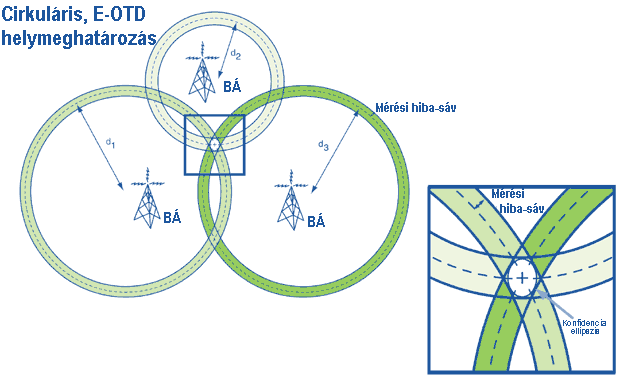
|
6.87 ábra - a kör modellű (cirkuláris) E-OTD helymeghatározás vázlata
|
Amint a (38) képletből, illetve a 6.87 ábrából is látható az ismertetett E-OTD elrendezés viszonylag egyszerűen szolgáltatja a metsző körök felhasználásával a keresett állásponti koordinátákat. Az irodalomban hátrányként említik, hogy viszonylag lassú, mintegy 5 másodperc az eredmény meghatározása.
Ugyanezt a rendszert - más algoritmussal hiperbola navigációra is lehet használni, bár valójában inkább az Érkezési Időkülönbség (TDoA) Módszer illeszkedik erre a geometriára. (Sajnos a jelenlegi gyors fejlődés még nem tette lehetővé, hogy a különböző módszereket minden szerző illetve cég azonosan értelmezze).
A TDoA módszer lényege, hogy a Mobil Állomás által kibocsátott jeleket 2 - 2 Bázis Állomás veszi és meghatározza az útkülönbséget a Bázis Állomások és a Mobil Állomás között. Ha a Bázis Állomás párokat úgy tekintjük mint egy-egy hiperbola gyújtó pontjait, akkor a Bázis Állomásoktól mért távolság különbségek mértani helye egy hiperbola (6.88 ábra).
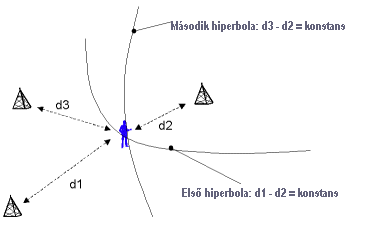
|
6.88 ábra - a hiperbola navigáció a TDoA rendszer alkalmazásakor
|
Amint az ábrából is látható bizonyos esetekben két hiperbola is megadja az álláspontot, a működő rendszerek azonban legalább három hiperbolát használnak. A módszer előnye, hogy kiküszöböli a Mobil Állomás óra hibáját, igényli ugyanakkor, hogy a Bázis Állomások órái szinkronizáltak legyenek. Ez a rendszer is hálózati rendszer, nem igényel módosításokat a mobil telefonokban.
A Mobil Állomáson Történő Érkezési Időmérés (ToA) módszere megméri egy sor Bázis Állomásról (tulajdonképpen 3 elég lenne) a Mobil Állomásra jutó, azonos időben kibocsátott jel érkezési idejét. Ebből kiszámítja a Mobil Állomás és a Referencia Állomások közötti távolságokat és redundáns méréseket feltételezve kiegyenlítéses ívmetszéssel kiszámolja a Mobil Álláspontját. A módszer csak akkor működik, ha a Mobil Állomások és a Referencia Állomások órái szigorúan szinkronizáltak. Mivel ez mind a hálózat, mind a telefon módosítását igényli a jelenlegi második generációs rendszerekben (pld. GSM) nem használják, és üzembe állása csak a harmadik generációs rendszerekben várható.
A felvázolt helymeghatározó módszerek közül a GSM rendszerben a TDoA és az E-OTD 67%-os valószínűségi szinten 50 - 120 méteres pontosságot tesz lehetővé. A nagyobb hibákat a városi környezetben gyakori visszaverődések okozzák. A következő generációs UMTS szabvány szerinti telefonok 2 GHz-es vivő frekvencián fognak működni, 5 MHz-es moduláló frekvenciával. Ezek a paraméterek jelentősen csökkentik a mérési zajt és a visszaverődésekből eredő hibákat. A várható pontosságok az új generációs rendszereknél továbbra is 67%-os valószínűségi szinten a TDoA és az E-OTD módszerek esetében várhatóan 5 - 20 m. lesz, míg a ToA módszer várható pontosságát 50 - 100 m.-re becsülik.
Az előző bekezdés alapján bízvást állíthatjuk, hogy 3. generációs mobil telefon rendszerek térhódításával indokoltnak látszik integrálásuk a gépkocsi navigációs rendszerbe, bár ennek célszerűsége nem csak attól függ, hogy az optimista hibaprognózisok realizálódnak-e, hanem attól is, hogy a helymeghatározási szolgáltatás milyen fizetési feltételekkel lesz elérhető.
Távközlési Technikák
Ha az ITS rendszer egészét nézzük, úgy a jelen és jövő távközlési technikáinak egész arzenálját kellene ismertetnünk, hiszen a felvázolt amerikai ITS rendszer 30 szolgáltatásának döntő többsége feltételez egy, két vagy többoldalú kommunikációt.
Az általunk tárgyalt gépkocsi navigációban alapvetően a friss közlekedési adatok, illetve DGPS alkalmazása esetén a differenciális korrekciók vételére van szükség. E mellett a sok járművel rendelkező intézmények vagy cégek (pld. Rendőrség vagy Hungarokamion ) a járatok szervezéséhez az úgynevezett flotta menedzsment rendszereket használják, melyek működéséhez a központnak információval kell rendelkeznie az egységek helyéről, állapotáról, arról nem is beszélve, hogy a központ utasításait is továbbítani kell az úton lévő autókhoz.
Ha az egész ITS spektrumára gondolunk, akkor a következő távközlési rendszerek figyelembe vételéről lehet szó:
- Nagy Térségi Rádió Adók (elsősorban azok az FM rádiók, melyek ha frekvencia váltással is végig vehetők az utazás folyamán);
- Nagy Térségi Duplex Drótnélküli Kommunikáció nagysebességű adathálózaton, vagy ami egyelőre gyakoribb, mobil telefonon;
- Specializált Rövid Távú Kommunikáció (angolul Dedicated Short Range Communications = DSRC), mely adó-vevői az út szélén felállított oszlopokról kommunikálnak az áthaladó gépjárművekkel;
- Gépkocsik közötti kommunikációs rendszerek;
- Vezetékes Kommunikáció - a hagyományos telefontól a nagy sebességű adathálózatokig.
A VHF tartományban sugárzó FM rendszerű műsorszóró rádiók segéd vivőfrekvenciáját (57 KHz.) felhasználva már elég régóta használják az úgynevezett RDS (Radio Data System) specifikációt, mely lehetővé teszi adatok továbbítását alacsony - 1187.5 bit/s sebességgel.

|
6.89 ábra - a Volvo Systems Dynaguide nevű gépkocsiba szerel PC alapú rendszere megjeleníti az aktuális közlekedési információt
|
A 6.89 ábrán annak a gépkocsiba szerelt, PC alapú vevőnek a képernyőjét látjuk, mely az Arizónai Közlekedési Hivatal friss közlekedési információit jeleníti meg. Az információt kódolták, majd a GPS differenciális javításokkal együtt kisugározták a KSLX FM 100.7 rádióállomásról. Külön szoftver gondoskodott arról, hogy az információt az ETAK Phoenix-i úttérképén megjelenítse.
Hasonló kísérletet hajtottak végre 1997-ben Minnesota államban, a Minneapolis - St. Paul iker városok környékén is. Ennél a tesztnél ugyancsak a Volvo Dynaguide gépkocsiba épített rendszert használták, de a vizsgálatokat két adat specifikációra is elvégezték. Az RDS rendszer három színtű információt közvetít: szimbólumokat, jeleket és szöveget. A grafikus elemeket a rendszer felhelyezi a térképre. A FM Subsidiary Carrier Authorization (FM-SCA) technológia azonban ezen túlmenően még képes a vezető által kiválasztott félmérföldnyi útszakasz forgalom sűrűségi vagy sebességi viszonyainak folyamatos frissítésére is.
Az újabb törekvések a segédvivőn alapuló nagyobb adatátviteli sebességű rendszerek kialakítására irányulnak. Japánban kidolgozták a DARC rendszert, mely 6210 bit/s sebességű adattovábbítást tesz lehetővé. A rendszert továbbfejlesztették az Egyesült Államokban superDARC néven, mely adattovábbítási sebessége eléri az 57 600 bit/s-t. A fejlesztés 4 évig tartott és 13 millió $, főleg állami pénzt emésztett fel. Mivel a project még nem fejeződött be terepi kipróbálásáról még nem tudok beszámolni.
A superDARK projekt sikere mindenesetre erősen valószínűsíti azt az elképzelést, hogy a jövőben a CD-n kapható utcatérképek attribútumait folyamatosan, FM rádiók segítségével fel lehet frissíteni aktuális forgalmi információkkal. Természetesen a technikai kérdéseken túl szervezési és pénzügyi kérdéseket is meg kell oldani: ki és milyen kiméretben szolgáltasson ilyen információt, és melyik rádióadó milyen információt sugározzon, azaz melyik sugározza a teljes attribútum felfrissítést, melyik sugározza a gyorsan változó forgalmi jellemzőket, melyik sugározza az egyéb utazási-turisztikai információt.
A Nagy Térségi Duplex Drótnélküli Kommunikáció amint már említettük jelenleg elsősorban a mobil telefon hálózatokon keresztül realizálható az autonavigációban. Tulajdonképpen a duplex jellegre csak flotta menedzsment alkalmazásokban van szükség. Figyelembe véve hogy már a jelenlegi GSM hálózat 9600 bit/s adattovábbítási sebességét is 14 400 bit/s-re tervezik felemelni, továbbá, hogy az úgynevezett HSCSD technológia segítségével további sebességnövekedés érhető el (57 600 bit/s), igaz a hálózat módosításával, a mobil telefonok már a közeljövőben is konkurálhatnak a műsorszolgáltató rádiókkal is a navigációs rendszer közlekedési adatbázisának felfrissítésében. Ugyanez a sebesség a következő generációs UTMS rendszerű telefonok esetében legalább egy nagy nagyságrenddel megnő, ami további lehetőségekkel kecsegtet a gépkocsin belüli adatelérésben. Persze azt nem szabad szem elől tévesztenünk, hogy míg a műsorszóró rádió teljesítményét nem befolyásolja, hogy hányan veszik, addig a mobil telefonoknál a felhasználók számának növekedése, különösen ha valamennyien ugyanazt a szervert kívánják elérni, hálózati problémákat is okozhat.
Ezzel is magyarázható, hogy például az amerikai its program keretében számtalan egyéb szélessávú drótnélküli adathálózat tervezésével is foglalkoznak, és nem csak olyanokkal, melyek fix helyzetű állomások között kommunikálnak, hanem olyanokkal is melyek mozgó végponttal rendelkeznek.
A Specializált Rövid Távú Kommunikációt (angolul Dedicated Short Range Communications = DSRC) csak a teljesség kedvéért említjük, mivel funkciói alapvetően nem navigációs jellegű feladatok megoldására irányulnak. Ezek az út menti oszlopokra szerelt adó-vevők kezdeményezik a gépkocsi adójának aktivizálódását, érzékelik a gépkocsi adójából érkező jeleket és azok alapján valamilyen specializált feladatot látnak el. Ilyen feladat lehet például az útdíj levonása vagy számlázása, a közúti jelzőlámpák zöldre állítása különleges jelzésű gépjármű előtt, a tehergépkocsi elektronikus szállítólevelének ellenőrzése, stb., stb.
A Gépkocsik Közötti Kommunikációs Rendszerek céljaira rövidtávú (néhány 100 m. hatósugarú) a milliméteres vivő hullám tartományban működő kommunikációs rendszerek kidolgozásán dolgoznak Japánban és az Egyesült Államokban, melyek tervezett célja a gépkocsik összeütközésének automatikus elhárítása.
A Vezetékes Kommunikációs Technikák továbbfejlesztése a Területi Közlekedési Műveleti Központok gyors és megbízható adatátviteli kapcsolattal való összeköttetését célozza.
A gépkocsi navigáció funkcióit és alkalmazási területeit a fentiekben már elég részletesen felvázoltuk. Ebben a pontban néhány olyan kereskedelmi hardver-szoftver terméket mutatunk be, melyek a gyakorlatban is bemutatták használhatóságukat.
- 750NAV GPS Gépkocsi Navigációs és Gépkocsivezető Információs Rendszer.
A portábilis (egyik gépkocsiból a másikba helyezhető) rendszert a Magellan cég készíti.

|
6.90 ábra - a Magellan 750 NAV nevű gépkocsiba helyezhető navigációs és vezető információs rendszere
|
A rendszer nem használ CD-ket a térkép fedvények az USA-ról és Kanadáról, valamint a legkülönbözőbb információs anyagok a memóriában vannak elhelyezve. A berendezés PC kompatibilitását a jövőben igérik megvalósítani.
A helymeghatározást GPS, egy VIP-nek nevezet független navigációs rendszer és térképillesztés biztosítják, mintegy 15 m.-es pontossággal. A VIP-ről csak annyit tudhatunk meg, hogy önálló szenzorai vannak, nem kell az ABS-re kapcsolni, ez feltehetőleg azt jelenti, hogy Inerciális Navigációs Rendszert használ. Érdekessége a rendszernek, hogy hangos utasításokat is generál.
- A Snap Track Rendszer tulajdonképpen olyan nyílt technológiai modul, mely sokféle alkalmazásba, többek közt gépkocsi navigációsba is beépíthető. A rendszer érdekessége (ezért is szerepel a felsorolásunkban), hogy a mobil telefonok helymeghatározó képességén alapul.
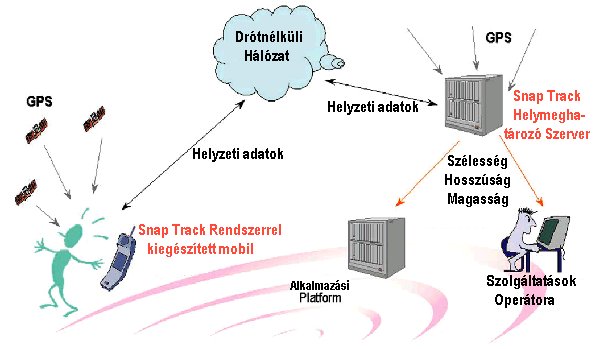
|
6.91 ábra - a Snap Track Rendszer működési sémája
|
A felhasználói oldalon a rendszer egy GPS vevővel kiegészített mobil (vagy drótnélküli) telefon, mely helymeghatározási műveletet kezdeményez. A telefon jelét a mobil (vagy más duplex adathálózat) a helymeghatározó szerverhez továbbítja. A szerver meghatározza a mobil közelítő helyét (leggyakrabban a cella azonosító alapján) és kiválasztja, hogy arról a helyről milyen műholdak láthatók, majd ezt üzenetben megküldi a mobilnak. A GPS vevővel kiegészített mobil elvégzi a távolság meghatározást a kijelölt műholdakra és az eredményt elküldi a helymeghatározó szervernek. A szerver a mobil mérési adataiból, valamint egy referencia GPS vevő adataiból, melyet a szerver közelében telepítettek kiszámítja a mobil szélességét, hosszúságát és magasságát és megküldi valamely alkalmazási központnak (pld. mentőknek, rendőrségnek, flotta diszpécser központnak, stb.) esetleg magának a mobilnak is (6.91 ábra). Ez utóbbi esetben a mobilt egy PC-hez kapcsolva a rendszer gépkocsi navigációra is használható.
- A SiRF cég GPS technológiája olyan GPS vevőt és szoftvert kínál, mely a számítógéppel különböző szinteken (külső egységként, PCMCIA kártyán vagy alaplapra szerelten) integrálható. Azt, hogy a vevőt kifejezetten navigációs célokra tervezték következő rendszer funkciói bizonyítják:
- Térképi adatbázis alapján szűri a helyzeti adatokat;
- Háromnál kevesebb látható szatellita adatait is fel tudja használni a helymeghatározáshoz (abból indul ki, hogy a gépkocsi korábbi útvonalán halad és a hiányos adatokból csak a megtett távolságot számítja, amint ismét láthatóvá lesz három műhold az esetleges pozicionálási hibát korrigálja);
- "Snap Lock" nevű opciója lehetővé teszi, hogy a műholddal megszakadt kapcsolatot kevesebb mint 100 ms alatt helyreállítsa;
- Fokozott érzékenysége következtében részleges takarás esetén is, például fasorban, tudja venni a GPS jeleit;
- Külön alrendszerrel biztosítja a többszörös visszaverődésből származó hibák csökkentését.
- Az ALPINE autórádió gyár Mobile Multimedia Station System nevű terméke a szórakoztatáson kívül mindazokkal a navigációs képességekkel rendelkezik, melyeket e lapon összefoglaltan ismertettünk. Fő szenzora a GPS, de e mellett giroszkópot és fordulatszámlálót is alkalmaz a takart szakaszokon, illetve az ábrázolás pontosságát térkép illesztéssel fokozza. A térképi adatokat és hozzárendelt információt CD romokról olvassa. Részletes vezető tájékoztató rendszere hang utasításokkal is segíti a vezetőt.
- A TRIMBLE cég talán a legismertebb GPS gyártó hazánkban. Ez a cég, számtalan egyéb helymeghatározó alkalmazás mellett, külön rendszert ajánl a flotta menedzsment céljaira. A rendszer mozgó modulja a CrossCheck GPS és mobil telefon integrálásával helyzeti adatokat és üzeneteket továbbít a FleetVision 3.0 nevű Windows-os szoftvernek, mely a diszpécser-központban megjeleníti a képernyő térképen az egyes járművek aktuális helyzetét. Több mint 10000 járművet tud megjeleníteni. Ezen kívül a felhasználó megállapíthat olyan eseményeket, melyek bekövetkeztével riasztja a központot. A helyzeti adatokon kívül a gépkocsik egyéb szenzor adatai is (pld. a sebességmérő kijelzése) továbbíthatók a központba. Takarékossági okokból a telefonos adattovábbítás nem folyamatos, hanem csak előre megadott időpillanatokban megy végbe. Kivételt képeznek a rendkívüli események, melyek azonnal továbbításra kerülnek és riasztják a központot.
A közlekedés egészét tekintve a szervezett, automatizált rendszerek térhódítása megállíthatatlan. Az ITS főbb moduljainak realizálása nélkül a közúti közlekedés különösen a városokban még olyan kevéssé fejlett országban is mint Magyarország totálisan ellehetetlenülhet. Még inkább igaz ez az Egyesült Államokra, ahol a lakott települések a nem igazán bölcs családi házas település szerkezet következtében 50-100 kilométeres sugárba is szétterülnek. Ha ehhez hozzátesszük, hogy a tömegközlekedés nem igazán fejlett és még kevésbé népszerű, akkor belátható, hogy a csúcs időpontokban állandósuló dugók csökkentésére nem igazán van más lehetőség. Hasonló problémákat idéz elő Európa fejlett országaiban a távolsági tehergépjármű forgalom túlburjánzása.
Szűkebb témánkat, a gépkocsi navigációs rendszereket illetően megállapítható, hogy műszakilag a technológia kiforrott, várható, hogy az elkövetkező években egy gépkocsi navigációs szet költsége nem fogja meghaladni egy jó minőségű autórádió árát. Európában a fő probléma az, hogy ma még nem áll rendelkezésre egész Európára rendszeresen karbantartott, szabványos digitális úttérkép. Remélhetőleg az elkövetkező években ez a helyzet megváltozik és nincs messze azaz idő, amikor a hazánkba látogató külföldi turistáknak nem kell kikapcsolniuk - térkép hiányában - Hegyeshalomnál a navigációs rendszerüket.
A jövő legfontosabb feladata olyan szabványos szoftver rendszerek alkalmazása, melyek képesek felfrissíteni a CD-ről betöltött úttérképek attribútumait, esetleg grafikus állományát. A felfrissítéshez azonban nem csak megfelelő szoftver kell, hanem olyan szabványos attribútum adatok is, melyeket a Közlekedési Forgalmi Központok műsorszóró rádiók segédvivőin vagy mobil telefon hálózaton szabványos keretek között folyamatosan sugároznak. Ezeket az adatokat három fő csoportra lehet osztani: tartós változások (pld. forgalmi rend változás az egyirányú utca kétirányúsítása), ideiglenes, de elhúzódó változás (útfelbontás csatorna építés miatt), pillanatnyi forgalmi helyzet (dugó az Erzsébet hídon egy meghibásodott gépjármű következtében). Ezeknek a feladatoknak a megoldása elsősorban szervezési okokból nem könnyű, de remélhető hogy az elkövetkező 5 év érett megoldásokat fog szolgáltatni ezeken a területeken is.
(1) A tanulmány része az OTKA T 030 645, T 030 643 és T 031 719 témaszámokon folyó kutatásoknak.
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc