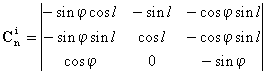Mobil térképező rendszerek
Ebben a részben megismerkedünk
- a mobil térképező rendszerek általános felépítésével,
- az inerciális navigációs rendszerek fogalmával és működési alapelveivel,
- Néhány megvalósult Mobil Térképező Rendszerrel.
A mobil térképező rendszerek
(angol elnevezéssel Mobile Mapping Systems vagy rövidítve MMS) a 80-as évek végén, 90-es évek elején jelentek meg északamerikai kísérleti műhelyekben, ipari-kísérleti alkalmazásukról az első közlemények 1995-96-ra datálhatók [17], [18].
A rendszer mozgó
szállítóeszközre erősített különböző érzékelőkből álló együttes, mely képes a
jármű pályájának folyamatos meghatározására, s egyben a szenzorok fajtájától
függő, kiegészítő térbeli információ gyűjtésére.
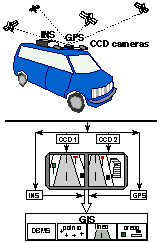
Ha egyszerűbben akarunk fogalmazni, akkor arról van szó, hogy egy furgont felszerelünk helymeghatározó műszerekkel és digitális kamarákkal és a furgon 60 km/óra sebességgel haladva képes nem csak a saját pályáját, de a környező utcaképet is geometriailag korrekten kiértékelhető módon rögzíteni. Szenzorként rendszerint CCD kamarákat alkalmaznak, de helyettük alkalmazhatnak:
- - képalkotó lézert;
- - profilozó lézert;
- - impulzus radart és
- - ultrahangos érzékelőt is.
A képalkotó lézer alkalmazása esetén a kép mellett a szenzortól mért távolságot is meghatározzák, ami növeli a meghatározás redundanciáját és pontosságát.
A lézer profilméréskor távolságot és szöget mérnek (pld. vasúti űrszelvény meghatározásához).
Az impulzus radarok képesek az objektumok vastagságának meghatározására is, rendszerint a burkolati hibák földerítésére használják.
Az ultrahangos érzékelők szintén poláris koordinátákat (távolságokat és szögeket) határoznak meg, utak hossz,- és keresztszelvény méréseinél kerülnek alkalmazásra.
Az érzékelők sora persze még folytatható volna (pld. az igen gyakran alkalmazott videó-kamerákkal) felsorolásunkban azonban csak azok szerepelnek, melyekből számítható helyzeti pontosság többé-kevésbé összhangban van a furgon pályájának meghatározási pontosságával.
A kocsi folyamatos helymeghatározására GPS vevőt és kiegészítő navigációs eszközökként vagy inerciális navigációs rendszert (angolul Inertial Navigation System - rövidítve INS) vagy kerék fordulatmérőket és pörgettyűs tájolókat használnak. Az INS-t használó mérőkocsik adatait is kiegészíthetik pld. az ABS blokkolásgátló rendszerek fordulatmérőivel.
A felmérés eredményét egyelőre utó-feldolgozási üzemmódban kapják meg, a jelenlegi kutatások jelen idejű adatszolgáltatást és az ehhez szükséges automatikus objektum kiértékelést célozzák meg.
Az olvasóban felmerülhet a kérdés, hogy a nagyfelbontású térképészeti műholdak megjelenése után lesz-e szükség ilyen rendszerekre. Nyugodtan válaszolhatjuk, hogy igen, elsősorban köz-, és vasutak pályái és szerelvényei, valamint városi utcák és utcaképek felmérésekor. Ezeknél az objektumoknál ugyanis a felmérendő objektumok jelentős része a függőleges síkban helyezkedik el, s ezért a közel függőleges tengelyű légi és műholdas felvételeken nem látható.
A kocsik helymeghatározását általában GPS, és INS segítségével hajtják végre, bár a kerekek fordulatméréséből is levezethető a relatív helymeghatározás (angolul dead reckoning DR), ez azonban viszonylag kevéssé megbízható, mivel függ pld. a keréknyomástól, futófelület kopottságától, stb.
Mivel a GPS-szel nagy vonásokban már megismerkedtünk, indokolt, hogy ha csak röviden is, fogalmat alkossunk az inerciális rendszerekről is.
Inerciális navigációs rendszerek
A 80-as évek elején az amerikai hadsereg számára gyártott inerciális navigációs rendszerek néhány típusát felszabadították a polgári használat céljaira és a geodéták hozzáláttak annak a vizsgálatához, hogy milyen feltételek mellett használhatók e rendszerek az alappontsűrítés automatizálására.
Bár az alkalmazásra gyakorlati feladatokban már csak azért sem került sor, mivel a műszerek akkor még igen drágák voltak (kb. 500 000 $), az elmélet kidolgozása igen hasznosnak bizonyult napjaink korszerűbb (kisebb, pontosabb, olcsóbb) rendszerei alkalmazhatósága szempontjából.
Az INR alpelvét legegyszerűbben úgy képzelhetjük el hogy létrehozunk egy háromdimenziós koordináta rendszert, mely a Földhöz képesti kezdeti helyzetét a jármű haladása közben nem változtatja meg, s az egyes tengelyekre szerelt gyorsulásmérők mérési eredményeit kétszeresen integrálva megkapjuk a jármű kezdeti helyzetéhez képest a megtett út koordináta vetületeit.
A rendszer gyakorlati megvalósításához tehát biztosítani kell a koordináta tengelyek mozdulatlanságát ezt a feladatot giroszkópok végzik, a tengelyekre mechanikusan gyorsulásmérőket kell szerelni, végül számítóegységet kell a rendszerhez kapcsolni a jelek gyűjtésére és kétszeres integrálására.
A 60-as, 70-es években kialakított rendszerekben a tengelyek stabilizálására pörgettyűket használtak. A pörgettyű tengelye giroszkópikus merevséggel rendelkezik azaz az inerciális koordináta rendszerhez képest helyzetét nem változtatja.
|
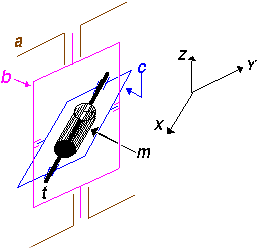
Az 3.119 ábrán egyszerűsítve bemutattuk a korai rendszerekben alkalmazott himbás megoldások alapelvét. Az m motor gyors forgása következtében a t tengely párhuzamos az X koordináta tengely kezdeti helyzetével (az ábrán látható koordináta rendszert az a járműtesthez rögzítettük). Ha a gépkocsi elfordul a Z tengely körül úgy a b keret az ábrán látható csapágyakban szintén elfordul a- hoz képest és a t tengely helyzete nem változik. (A feltüntetett elrendezés kompenzálja a jármű Y tengely szerinti elfordulását is, az X menti elfordulás kompenzálására azonban egy újabb himbával kellett volna még kiegészíteni az ábrát). |
Ahhoz, hogy a vázolt elrendezés céljainknak megfelelően működjön, azaz hogy a gyorsulást a kiindulástól a végpontig azonos tengely irányába mérje arra van szükség, hogy a b keretre mereven egy szerelőlapot erősítsünk, melyre szintén mereven felszereljük a gyorsulás mérőt. Mivel a navigáció hajók és repülők esetén igényli a jármű elfordulási szögeinek ismeretét is, az a testelfordulását a b kerethez képest szögadókkal mérték.
A bemutatott leegyszerűsített vázlatból is látható, hogy a stabilizált tengelyekkel működő berendezések igen szabatos mechanikai kialakítást igényeltek (pld. súrlódásmentes csapágyak, szögadók, stb.) és a finommechanika viszonylag lassabb fejlődése nem tette lehetővé, hogy a fenti megoldással pontos, olcsó és kisméretű rendszerek épülhessenek. Az újabb lehetőségeket a gyorsabban fejlődő optika és mikroelektronika szolgáltatták.
Az új típusú analitikus rendszerek létrejöttét a strapdown (leszíjazott = rögzített) giroszkópok felfedezése tette lehetővé. A rögzített giroszkópnak nincs stabilizált tengelye, melyhez gyorsulásmérőt rögzíthetünk, ez a giroszkóp tulajdonképpen nagypontosságú szögsebességmérő, mely sebességértékek idő szerinti integrálásából meghatározható a kezdeti állapothoz viszonyított, a giroszkóp tengelye körül végzett elfordulás.
Leggyakrabban lézer giroszkópokat alkalmaznak szögmérő egységként, de újabban szilárdtest megoldásokkal is találkozunk. A 3.120. ábrán felvázoltunk egy lézer giroszkópot, míg a 3.121. ábrán egy szilárdtest giroszkópot az u.n. Murata féle girócsillagot.
|
A lézergiroszkóp alapelve azon az 1881-ben
felfedezett törvényen alapul, hogy a mozgó testből kibocsátott fény sebessége
konstans marad az inerciális vonatkozási rendszerhez képest. Ha tehát a 3.120
ábrán látható optikai gyűrű nem forog, úgy a fénynek T=L/c
időre van szüksége az L optikai hosszúságú gyűrű körbejárására,
ahol c a fény terjedési sebessége. Ha azonban a gyűrű az
óramutató járásának megfelelő irányban forog, úgy annak a fénysugárnak, mely
szintén ebben az irányban járja körbe a gyűrűt
|
|
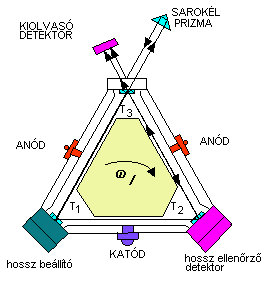
A klasszikus elv egyik viszonylag korszerű megvalósítási
formája esetében a HE-NE lézert közvetlenül a fényútba szerelik, melyet
három tükör T1,T2,T3 határol. A giroszkóp testét olyan anyagból készítik, melynek
gyakorlatilag nincs hőtágulása, az optikai út pontos beszabályozását szolgáló
elemekkel a fényút hosszát a hullámhossz n szeresére állítják,
ahol n egész szám. Mivel ez a rendszer üregrezonátorként működik
a végső leolvasás a ![]() formában jelenik meg, melyet az interferenciasávok
vándorlásának számlálásából vezet le a detektor.
formában jelenik meg, melyet az interferenciasávok
vándorlásának számlálásából vezet le a detektor.
A lézergiroszkópok korszerűbb változatai gáz helyett szilárdtest lézert használnak, a fény utat pedig száloptikában valósítják meg.
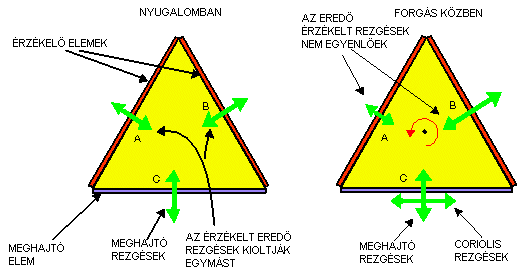
A Murata féle girócsillag működését az ábra
felirataival próbáltuk megmagyarázni.
Nyugalmi állapotban az alaplapot gerjesztő rezgések egyenesen terjednek a szimmetrikus
érzékelő lapok felé és így azok azonos feszültséget jeleznek. Ha - az ábrán
látható módon - a háromszöget elforgatjuk, úgy a hullámterjedés inerciális
jellege következtében, a B lapra érkezik azoknak a rezgéseknek
egy része is, melyek a C balfeléről indultak még abban a
helyzetben, amikor a C vízszintesen állt. A két érzékelőről
levett feszültségek különbségéből a szögsebesség értéke számítható.
|
|
Míg a giroszkópokban a hullámterjedés inerciális jellegét használták ki a fizikusok, addig a gyorsulás mérők a tömeg tehetetlenségén (Newton 2. törvényén) alapulnak. A legtöbb korszerű gyorsulásmérő az inga elvet kombinálja valamely piezoelektromos jellemzővel. Ezek kissé részletesebb ismertetése azonban meghaladná a fejezet kereteit.
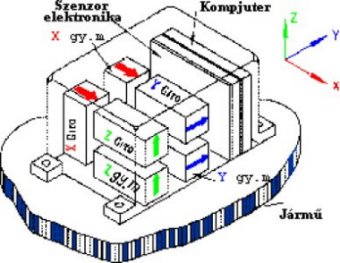
A 3.122. ábrán azt mutatjuk be, hogy hogyan is nézhet ki egy összeszerelt inerciális rendszer, ha a ház fedelét átlátszó anyagból készítenénk.
|
|
||||
|
Mivel az analitikus inerciális navigációs
rendszerekben nincsenek valódi inerciális tengelyek a mérési eredményeket
számítással kell transzformálni a jármű úgy nevezett test koordináta rendszerébe, illetve a földrajzi helyi függőleges (n) koordinátarendszerbe,
melyben a pont helyzetét a
|
A koordinátákon kívül mind a mobil térképező rendszereknek
mind a navigációs rendszereknek szükségük van még a jármű elfordulási
értékeire: a ![]() bukásra,
bukásra, ![]() dőlésre és
dőlésre és
![]() elfordulásra
(légi fotogrammetriában a repülőgép megfelelő elfordulás értékeiből keletkező
külső tájékozási adatokat
elfordulásra
(légi fotogrammetriában a repülőgép megfelelő elfordulás értékeiből keletkező
külső tájékozási adatokat ![]() betűkkel jelöltük) A valóban
navigációs célokat szolgáló rendszerekben ezen kívül még számítani kell a kívánt
cél eléréséhez szükséges pillanatnyi vezérlési adatokat is.
betűkkel jelöltük) A valóban
navigációs célokat szolgáló rendszerekben ezen kívül még számítani kell a kívánt
cél eléréséhez szükséges pillanatnyi vezérlési adatokat is.
A Litton cég a legrégibb INS előállító vállalat. A 3.124-es ábrán látható rendszert az amerikai légierő az F22-es repülőgépekbe és a Commanche helikopterekbe építi be.
|
|
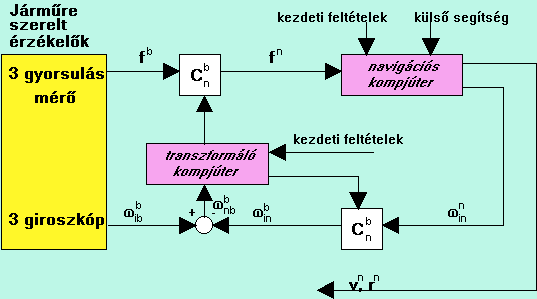
3.125 ábra - az inerciális rendszer számítási blokkvázlata |
A számítás első lépésében kalibrációs javításokkal látják el a gyorsulásmérők és a giroszkópok outputját.
A második lépésben a test koordináta rendszerből (b)
a navigációs koordináta rendszerbe (n) transzformáló mátrix ![]() számítására
kerül sor. Ez a számítás a következő differenciál egyenlet numerikus megoldásán
alapul:
számítására
kerül sor. Ez a számítás a következő differenciál egyenlet numerikus megoldásán
alapul:
![]() ,
,
ahol ![]() az
az
![]() vektorból
kialakított antimetrikus forma. Ugyanis, ha
vektorból
kialakított antimetrikus forma. Ugyanis, ha ![]() úgy
úgy 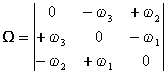 , (az egyenlet baloldalán a mátrix feletti
pont a differenciálás jele).
, (az egyenlet baloldalán a mátrix feletti
pont a differenciálás jele).
Az ![]() meghatározásához a navigációs rendszernek az
inerciális rendszerre vonatkozó szögsebesség vektorát
meghatározásához a navigációs rendszernek az
inerciális rendszerre vonatkozó szögsebesség vektorát ![]() -t ki kell
vonnunk visszacsatolás formájában a mért inerciális szögsebesség vektorból
-t ki kell
vonnunk visszacsatolás formájában a mért inerciális szögsebesség vektorból ![]() -ből,
azaz
-ből,
azaz
![]() .
.
A következő számítási lépésben a test koordinátában mért erőket (egységnyi tömegen
mért gyorsulásokat) alakítja át a rendszer a navigációs koordináta rendszerbe:
![]() ,
,
majd az átalakított értékeket betáplálja a navigációs kompjuterbe.
A nehézségi erőtér és a Föld forgásából eredő Coriolis
erő hatásainak kompenzálása után két egymást követő integrálás
eredményeképpen a rendszer kimenetén megkapjuk a vn sebességvektort
és az rn helyzetvektort. A vn vagy a szélesség és hosszúság szerinti
sebességkomponensek valamint a Föld forgássebessége ![]() alapján
alapján ![]() meghatározható,
s ennek segítségével a már fentebb említett visszacsatoláshoz szükséges
meghatározható,
s ennek segítségével a már fentebb említett visszacsatoláshoz szükséges ![]() számítható.
számítható.
Mivel a mobil térképező rendszerekben az elfordulásoknak döntő szerepe van lássunk néhány további összefüggést a mért értékek és navigációs rendszerbe transzformáltjaik között.
Induljunk ki a test koordináta rendszer és az inerciális
koordináta rendszer közti transzformációból: ![]() ,
,
|
ahol |
|
, |
|
, |
és |
|
Az eddig még nem tárgyalt jelölések a következők: ![]() az i
tengely körül j szöggel történő forgatás forgatási mátrixának
transzponáltja,
az i
tengely körül j szöggel történő forgatás forgatási mátrixának
transzponáltja, ![]() időhöz tartozó földrajzi hosszúság,
időhöz tartozó földrajzi hosszúság, ![]() a Föld
forgási sebessége.
a Föld
forgási sebessége.
Érdemes megjegyezni, hogy a transzformációs mátrixok
ortogonalitása miatt igaz, hogy ![]() , azaz a kiinduló és cél koordináta rendszert
a transzformációs mátrix sorainak és oszlopainak felcserélésével
megfordíthatjuk.
, azaz a kiinduló és cél koordináta rendszert
a transzformációs mátrix sorainak és oszlopainak felcserélésével
megfordíthatjuk.
Ha differenciáljuk a kiinduló transzformációt a következő kifejezésekre jutunk:
![]() .
.
Végül felírhatjuk, hogy mivel is egyenlő a giroszkópok által szolgáltatott
mérési eredmény: ![]() . Az
. Az ![]() a helyi függőleges rendszer
szögsebesség vektora az inerciális rendszerre vonatkoztatva, melyet a következő
képlettel írhatunk le:
a helyi függőleges rendszer
szögsebesség vektora az inerciális rendszerre vonatkoztatva, melyet a következő
képlettel írhatunk le:
![]() .
.
Az ![]() kifejezésében szereplő
kifejezésében szereplő ![]() szögsebesség vektort a
navigációs szögek szerinti forgatási mátrixok szorzatának differenciálásával
nyerhetjük az alábbiak szerint:
szögsebesség vektort a
navigációs szögek szerinti forgatási mátrixok szorzatának differenciálásával
nyerhetjük az alábbiak szerint:
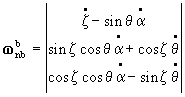 .
.
Talán a bemutatott képletek egy kissé
megkönnyítik annak az elképzelését, hogy hogyan lehet a másodpercenként 50
szögsebesség értékből meghatározni a jármű és a Földhöz kapcsolt referencia
rendszer forgatási mátrixát ![]() -t.
-t.
Az inerciális rendszerek általában az általunk (n)-betűvel jelölt földrajzi koordináta rendszerben dolgoznak. Természetes, hogy szükség esetén újabb transzformációval át tudunk térni ebből a rendszerből valamely rögzített helyzetű térbeli vagy síkbeli koordináta rendszerbe is. Ezért, a későbbiekben a helymeghatározás eredményét gyakran fogjuk (m) indexű koordináta rendszerben használni utalva ezzel arra, hogy a további transzformációkat már elvégeztük.
Néhány megvalósult Mobil Térképező Rendszer
Ha az irodalmat tanulmányozzuk (kongresszusi kiadványokat, szakfolyóiratokat, Internet home page-eket) három létező rendszerről találunk információt. Ezek a VISAT (Video-Inercial-SATellite) rendszer [20], a GPSVanTM [21] és a GPSVision [22].
Irodalmi adatok alapján a legkomplettebbnek a kanadai Calgary Egyetem Geomatika tanszéke és a Quebec tartomány Laval városában működő GEOFIT vállalat közös fejlesztése a VISAT tűnik. A 3.126. ábra vázlatosan bemutatja a rendszert, a 3.127 ábrán a gépkocsit látjuk, a 3.128. és 3.129. ábrák pedig a jobb és baloldali mérőtornyokat mutatják be.
|
Amint az ábrákról látszik a GPS, INR és a CCD kamarák a furgon tetején helyezkednek el. A baloldali ábra második része bemutatja, a kamarák által felvett képpárt, míg a harmadik rész arra utal, hogy a képek feldolgozásával milyen objektumokkal gazdagodik a GIS. A jobboldali képen jól láthatók a gépkocsi és a rászerelt az érzékelő együttes. |
|
|
A VISAT rendszer egyik érdekessége, hogy a furgon tetejére rögzített érzékelő blokkokban 8 CCD kamara foglal helyet (lsd. a bal és jobboldali ábrát). Ez lehetővé teszi, hogy az objektumot mindig azokból a képekből értékeljék ki, melyek tartalmi illetve pontossági szempontból a legtöbbet nyújtanak. |
|
A CCD kamarák vezérlését külön egység hajtja végre. E kamarákon kívül egy videókamara is része a rendszernek (a szerepéről nem sok szó esik a leírásokban), két L1/L2 GPS vevő, és egy INR gondoskodik a helyzet-meghatározásról, az ABS rendszer fordulatszámláló kimenetét az expozíciós időpontok kijelölésére használják (meghatározott távolságokra és nem eltelt időre exponálnak).
Az összes érzékelő egy pentium PC-hez van interfészelve, mely programozott megszakításokkal vezérli a különböző adatáramlatokat.
A mérési eredmények feldolgozására szolgáló munkaállomásra telepített szoftver együttest GEOSTATION-nak nevezték. A szoftver a kiválasztott és kiértékelt objektumokat GIS struktúrában tárolja. Az 1997 végén kibocsátott VISAT nevű feldolgozó programjuk már PC-n fut WINDOWS 95 alatt.
Az utóbbi új jelölést azért
alkalmaztuk mivel a térképezés nem csak az n-nel jelölt földrajzi
koordináta rendszerben történhet hanem pld. az UTM vagy más sík koordináta
rendszerben is. Természetesen ez utóbbi esetben az inerciális rendszer
illetve a GPS outputját előbb még át kell transzformálni az
ellipszoidi rendszerből a sík vetületi rendszerbe. |
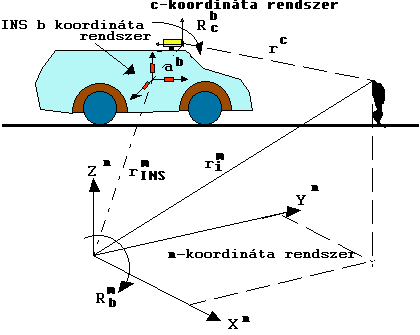
A 3.130 ábrán bemutattuk a mobil térképező rendszerben lévő koordináta rendszerek egy részét. Az inerciális navigációs rendszereknél tárgyaltakhoz képest két változást figyelhetünk meg. Megjelent a c-vel jelölt kamara koordináta rendszer, melynek kezdőpontja valamelyik kamara objektívjének vetítési középpontja, másfelől az eddig n-nel jelölt földi koordináta rendszert az ábrán m-mel jelöltük. |
Feladatunk az i indexű pont helyzetvektorának
(derékszögű koordinátáinak) meghatározása a térképezés m koordináta
rendszerében:
![]() ,
ahol rmi a meghatározandó pont keresett koordináta
hármasa az m rendszerben, rINRm (t)
az inerciális rendszer kezdőpontjának koordinátái az m rendszerben
(tulajdonképpen ezeket az értékeket határozzuk meg az inerciális rendszer és a GPS
integrálásából), (t) a fényképezés időpillanata, Rmb(t)
a b kordináta rendszerből az m-be forgató forgatási mátrix (az
előző pontban amikor a térképezés koordinátarendszere az n volt ezt a
mátrixot Cnb -nek neveztük), Rbc
a kamara koordináta rendszer és a test koordináta rendszer közötti
differenciális forgatási mátrix (a két koordináta rendszer tengelyeit
igyekeznek párhuzamosan elhelyezni) - elemeit a kalibráció során határozzák meg
a mérés előtt, rc az objektum koordinátái a képkoordináta
rendszerben, ab a c rendszer kezdőpontjának
koordinátái a b rendszerben (szintén a kalibrálás során mérik), Si
méretarány tényező, mely az egy pont - egy kamara viszonyra jellemző.
,
ahol rmi a meghatározandó pont keresett koordináta
hármasa az m rendszerben, rINRm (t)
az inerciális rendszer kezdőpontjának koordinátái az m rendszerben
(tulajdonképpen ezeket az értékeket határozzuk meg az inerciális rendszer és a GPS
integrálásából), (t) a fényképezés időpillanata, Rmb(t)
a b kordináta rendszerből az m-be forgató forgatási mátrix (az
előző pontban amikor a térképezés koordinátarendszere az n volt ezt a
mátrixot Cnb -nek neveztük), Rbc
a kamara koordináta rendszer és a test koordináta rendszer közötti
differenciális forgatási mátrix (a két koordináta rendszer tengelyeit
igyekeznek párhuzamosan elhelyezni) - elemeit a kalibráció során határozzák meg
a mérés előtt, rc az objektum koordinátái a képkoordináta
rendszerben, ab a c rendszer kezdőpontjának
koordinátái a b rendszerben (szintén a kalibrálás során mérik), Si
méretarány tényező, mely az egy pont - egy kamara viszonyra jellemző.
A vektor egyenlet négy ismeretlent tartalmaz: rmi három koordinátáját és az Si méretarány tényezőt három egyenletben, a vektor egyenlet ugyanis három skaláris egyenletre bontható. Ha ugyanaz a pont N képen képződik le úgy a meghatározás szabadságfoka (3N-3-N). Ha tehát a kérdéses pont csak két képen van rajta úgy a meghatározás szabadságfoka 1.
A rendszer 30 cm-es meghatározási pontosságot célzott meg, ehhez a GPS/INR helymeghatározást 10-15 cm-es pontossággal kell végezni, az INR szögértékei 1'-5' pontosak, a kalibrálás során mért távolságok 2-5 mm hibával terheltek, a kalibrált szögértékek pedig 1'-5' pontosak. A fotogrammetriai kiértékelés pontossága 0.5 pixel.
A rendszer működésének megkezdése előtt a kamarák belső adatait önkalibráló sugárnyaláb kiegyenlítő eljárással határozzák meg. Teszt-pontmező fényképezésével és kiegyenlítésével pedig meghatározzák a kamarák és INR kölcsönös helyzetét. A cél érdekében a kiegyenlítésbe olyan kiegészítő feltételeket visznek be, melyek a két rendszer egymáshoz viszonyított mozdulatlanságán alapulnak.
A kísérleti mérések során 30 m-es maximális kamara - objektum távolság esetén a középhiba nem haladta meg vízszintes értelemben a 16 cm-t, magassági értelemben pedig a 7 cm-t.
|
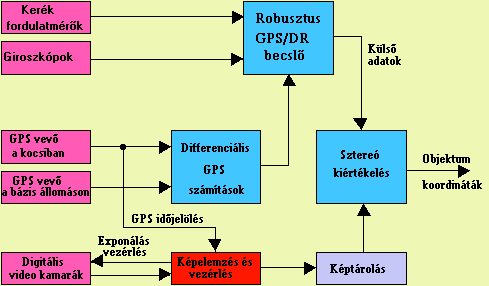
A GPSvanTM rendszert az Ohio Állami Egyetem Térképészeti
Központjában fejlesztették ki az elmúlt 5 évben. A rendszer furgonját a
3.131, blokksémáját pedig a 3.132 ábrán mutatjuk be. |
|
Mivel a kocsi helyzetét magasságilag is meg kell határozni ez csak akkor lehetséges, ha a pozicionálásba a bukás értéket mérő giroszkóp szögértékeit is bevonják, valószínű azonban (bár erről az ismertetőben nem szólnak), hogy a giroszkópok leolvasásait a másik két koordináta növekmény számításához is felhasználja az angolul dead-reckoning-nak (DR) nevezett relatív helymeghatározó rendszer. A robusztus becslő mibenlétéről sincs szó az ismertetésben, de erősen valószínűsíthető, hogy ez a rendszer is Kalman szűrőt használ.
|
|
A gépkocsi két db. 1.8 m.-es bázison rögzített CCD kamarával van ellátva. Az ipari-kísérleti feladatokhoz 768x480 pixeles kamarákat használtak. Mivel ez a kamara viszonylag durva felbontásával már 10 m tárgytávolság esetén eleve 5-15 cm hibával terheli a mérést, kísérleteket végeztek 1000x1000 pixeles kamarákkal is, melyekkel elérhető, hogy a felbontásból eredő hiba 5 m tárgytávolság esetén kevesebb mint 3 cm, 25 m tárgytávolság esetén pedig kevesebb mint 15 cm legyen. Mégis, az ipari mérések vizsgálata (több mint 9000 km vasúti váltó és egyéb vasúti jelölés felmérése) azt bizonyította, hogy az átlagosan 50 cm hiba főrészét kb. 30 cm-t a DR rendszer okozza.
|
A Lambda Tech. International GPSVision nevű rendszerének leírásából két olyan kérdésre is választ kapunk, melyekről az előző ismertetések hallgattak: milyen típusú GPS észlelést alkalmaznak és milyen formában használják a Kalman szűrőt. |
|
Előbb azonban ismerjük meg a rendszer
általános jellemzőit.
Az első generációs GPSVision egység egy Trimble ProXL kód-fázis GPS vevőből,
egy Liton LN-200 inerciális navigációs rendszerből, és két nagyfelbontású
szines CCD kamarából áll. Lehetőség van más GPS alkalmazására is pld. a Trimble
SSI GPS vevőt használják ha a pontmeghatározás pontossági igénye 10-20 cm.
Másik érdekes tulajdonsága a rendszernek, hogy az érzékelők a 3.134. ábrán
látható dobozba vannak szerelve és tetszés szerinti gépkocsira felerősíthetők.
|
|
3.134 ábra - a GPSVision rendszer mérődoboza |
A rendszer a GPS távolságok kettős különbsége
alapján működik. Ha i és j jelöl két műholdat, b az ismert
bázis ponton álló GPS vevő helyét, r pedig a mozgó vevő helyét,
tehát a mérőkocsit, akkor a mért távolságok különbségére felírható, hogy
egyenlő a koordinátákból számolható távolságok különbségével. Jelöljük R-el
az úgynevezett pseudo távolságokat, ![]() -val a koordinátákból számítható
távolságokat (pld.
-val a koordinátákból számítható
távolságokat (pld. ![]() ), akkor
), akkor
![]() .
.
Mivel a műholdak koordinátáit ismerjük, a bázis állomás koordinátáit szintúgy,
a R értékeket megmértük, a kifejezésben csak az r három
koordinátája az ismeretlen. A megoldáshoz tehát három kettős
távolságkülönbségre van szükség, amihez legalább négy olyan szatellita
szükséges, mely mind a mozgó, mind a bázis állomásról észlelhető.
A Kalman szűrő olyan matematikai eljárás, mely a dinamikus modell felhasználásával megbecsüli valamely k+1 időpontban a rendszer állapotát, és egybeveti ezt az értéket valamely pontos értékkel a kérdéses időpontban. A rendszer statisztikai tulajdonságai valamint a becsült és mért értékek eltérése alapján a módszer megjavítja a vizsgált szakaszra (a két mérés közé) eső előzetes értékeket és a folyamat folytatódik.
A GPSVision decentralizált szűrő módszert alkalmaz, melynek az a lényege, hogy nem számolja ki a Kalman féle becsült értékeket hanem e helyett az inerciális rendszer outputját használja. A simítás javítása érdekében a szűrőeljárást mindkét irányba lefuttatják.
A külső adatokkal ellátott képek kiértékelésére WINDOWS NT/95 alatt futó felhasználóbarát programrendszert is kidolgoztak. A rendszer lehetővé teszi a képek szemlélését, képpárok összeválogatását és a felhasználó által kijelölt objektum szemi-automatikus kiértékelését.
Bár a Mobil Térképező Rendszerek egyelőre még csak gyakorlati felhasználásuk kezdeti stádiumában vannak nem nehéz megjósolni, hogy néhány éven belül nélkülözhetetlenek lesznek a vonalas létesítmények, városok, közművek, ingatlanok, stb. felmérésében.
ˇ a következő részben a digitalizálással történő adatnyerést foglaljuk össze
ˇ esetleg visszatérhet az előző részhez
ˇ illetve a tartalomjegyzékhez
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc