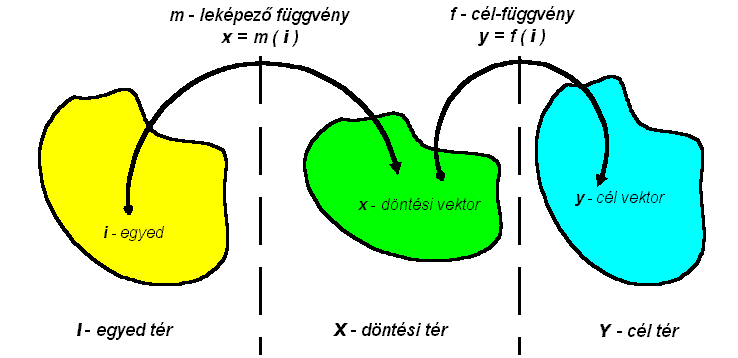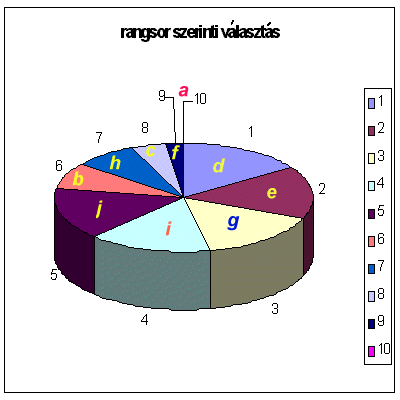GIS alkalmazások I (folytatás) ⁽¹⁾

Térbeli Döntéstámogató Rendszerek - TDR (folytatás)

Döntéstámogatás az IDRISI GIS szoftverben

Az IDRISI azok közé a ritka GIS szoftverek közé tartozik, melyek sztenderd függvényei között direkt eszközöket találunk a döntéstámogatásra, pontosabban fogalmazva a döntéstámogatásnak azokra az eseteire is, melyek meghaladják a valamilyen szempontból szükséges tulajdonságok összességét tartalmazó helyek megtalálását eredményező "overlay" technikákat.

A döntéseket a következő csoportokba foglalhatjuk:

• egy cél - egy kritérium;
• egy cél - több kritérium;
• több cél - több kritérium.

Az egy célt egy kritériummal leíró feladat nem igényel külön eszközöket a GIS-től. Mindössze arra van szükségünk, hogy a kritériumot összhangba hozzuk a megjelenített fedvény attribútumaival. Azaz, ha például egy lejtő kategória térképpel dolgozunk, melyen a lejtések 1 %-os lépcsőkben vannak ábrázolva a mi kritériumunk pedig az, hogy a keresett hely lejtése nem lehet nagyobb 5%-nál, úgy nem kell mást tennünk mint átosztályozni a képet oly módon, hogy a 0-1, 1-2, 2-3, 3-4, 4-5 százalékos lejtésű cellák 1 értéket kapjanak a többiek pedig 0-t. A megjelenített új képen az 1 értékű cellák jelentik a megfelelő helyeket.
Már ez az egyszerű feladat is bonyolódik azonban, ha bár megengedjük az 5%-os lejtést, de azért arra törekszünk, hogy lehetőleg minél síkabb legyen a kiválasztott terület. Ebben az esetben meghagyjuk az 5% alatti lépcsőket és úgy választjuk a területet, hogy lehetőleg minél kisebb lejtésű pixelekre essen (ne felejtsük el, hogy egy kritérium van, tehát ebben a feladatban nem adhatjuk meg a szükséges terület nagyságát is).
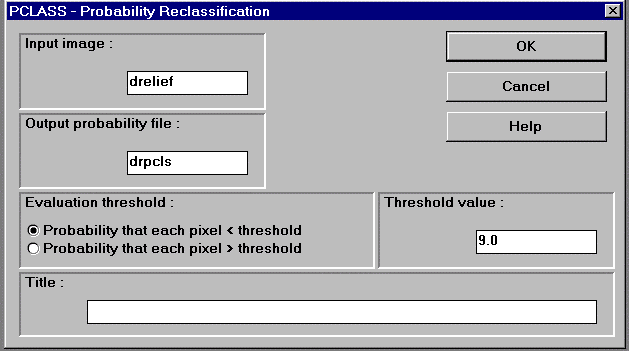
Mivel a GIS adatbázisban szereplő értékek nem hibátlanok az IDRISI-ben lehetőség van e hibák okozta kockázat figyelembe vételére is. Képzeljük el, hogy egy folyó mértékadó áradása 9 méteren következik be. Ha a terepről rendelkezésünkre álló magasságmodell nem hibás, úgy az áradáskor minden olyan terület víz alá kerülne, mely a kérdéses 6 méteres színt alatt van. A PCLASS modul segítségével azonban megnézhetjük, hogy mi a valószínűsége annak, hogy ez bekövetkezzen.

6.11 ábra - a PCLASS modul vezérlő panelja

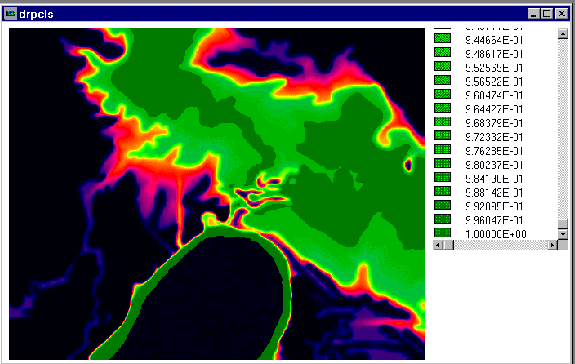
6.11 ábra - a "puha" osztályozás eredménye

A PCLASS-tól azt kérdeztük meg, hogy mi a valószínűsége annak, hogy minden pixel alacsonyabb a küszöbnek megadott 9 m-nél, az eredményt a 6.12 ábra tartalmazza. A sötétzöld értékek 1 körüliek, a világosabb zöld 0.96, a következő 0.91, stb. Ezután döntenünk kell a kockázati tényezőről, ha például 5%-ban állapítjuk meg, akkor átosztályozzuk a szelvényt úgy, hogy minden pixel ami nagyobb 0.95-nél 1 lesz, a többi 0, és az elárasztott területnek az előbbit tekintjük.

Az egy cél - több kritérium típusú feladat a leggyakoribb a GIS-ben, s mivel ennek a megoldásán alapul a következő legáltalánosabb feladat típus is, megkíséreljük összefoglalni a megoldás lehetséges módszereit.
A tényezőket (pld. lejtő kategória, távolság az utaktól, stb.) egy-egy réteg ábrázolja. A konkrét pixel értékeknek minden rétegen osztályzatokat adunk abból a szempontjából, hogy mennyire alkalmasak a cél megvalósítására . Ezeket az osztályzatokat minden rétegben azonos skálára húzzuk szét a STRECH modullal. Rendelhetünk a rétegekhez bináris, korlátozásokat is (ezek a réteg bizonyos pixel értékeire zérus, a többire egység értéket vesznek fel). A következő lépésben a tényezők súlyait határozzuk meg a páronkénti összehasonlítás módszerével.
Ez a módszer mindig két tényező egymáshoz viszonyított fontosságát értékeli az alábbi skála felhasználásával:

1/9	1/7	1/5	1/3	1	3	5	7	9
különösen	nagyon erősen	erősen	mérsékelten	egyenlően	mérsékelten	erősen	nagyon erősen	különösen

kevéssé fontos

nagyon fontos

6.1 táblázat - a páronkénti összehasonlítás érték skálája

Ha most már valamely cél eléréséhez a következő faktorok figyelembe vételére van szükségünk:

• út közelség
• város közelség
• lejtés
• tanyaközponttól való távolság
• parktól való távolság

akkor a feladat ismerete alapján például a következő összehasonlítási mátrixot írhatjuk fel. Megjegyezzük, hogy a mátrix szimmetrikus a főátlóra ezért elég csak a bal alsó háromszög mátrixot kitölteni, ha a súlyok meghatározásához az IDRISI WEIGHT modulját használjuk.

	út közelség	város közelség	lejtés	tanyaközpont távolság	park távolság
út közelség	1	3	1	7	2
város közelség	1/3	1	1/4	1/2	1/2
lejtés	1	4	1	7	2
tanyaközpont távolság	1/7	2	1/7	1	1/4
park távolság	1/2	2	1/2	4	1

6.2 táblázat - a faktorok páronkénti összehasonlítása

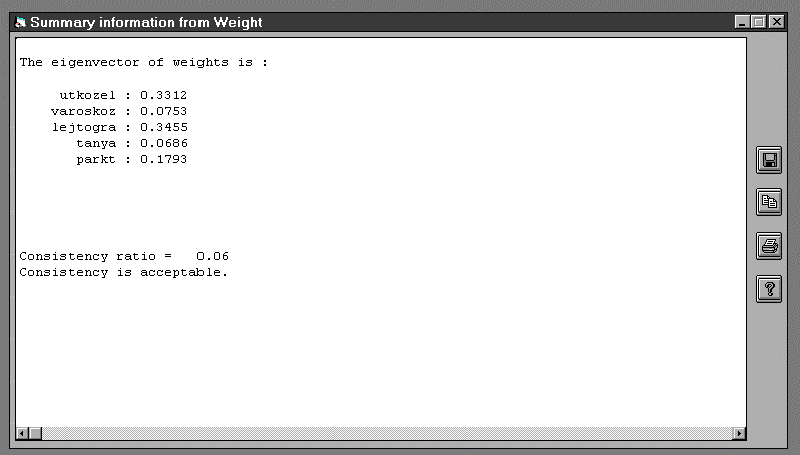
A páronkénti összehasonlítás mátrixából a keresett súlyokat a fő sajátvektor szolgáltatja. Ha nem áll rendelkezésünkre megfelelő szoftver, úgy közelítésként azt a megoldást is alkalmazhatjuk, hogy minden tagot az első, második, ... ,ötödik oszlopban elosztjuk a megfelelő oszlop összegével, majd vesszük az így kapott értékek soronkénti átlagát, melyek a legtöbb esetben jól közelítik a keresett súlyokat.

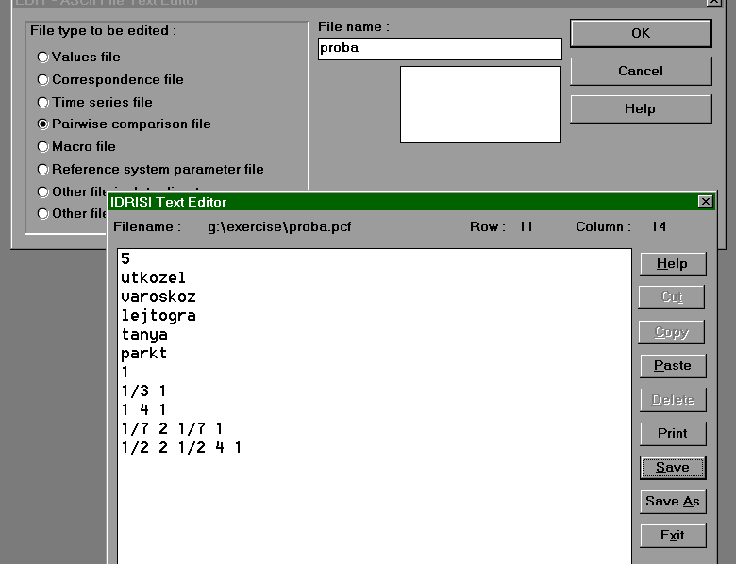
A feladatot egyszerűbben a WEIGHT modul segítségével oldhatjuk meg. Először az EDIT modulban a "Pairwise comparison file" feliratú rádió gomb bejelölése után a látható formátumban (bal alsó háromszög) bebillentyűzzük a mátrixot a szerkesztőbe és .pcf kiterjesztéssel mentjük.

6.12 ábra - a páronkénti összehasonlítás mátrixának megszerkesztése az EDIT modulban

Ezután meghívjuk a WEIGHT modult, megkeressük a fájl nevünket és OK-t nyomunk, az ennek eredményeképpen lefutó eljárás pedig az alábbi listát szolgáltatja:

6.13 ábra - a WEIGHT modul panelja és az erdmény súlyok listája

Ezután már minden rendelkezésünkre áll, hogy meghatározzuk a kérdéses cél alkalmassági térképét az alábbi összefüggés segítségével:

A = ∑ w_i·x_i ∏ c_j   (6.1),

ahol A - az alkalmassági érték, w_i - az i-edik faktor súlya, x_i - az i-edik faktor osztályzati értéke, c_j - a j-edik korlátozás értéke. A képletet kiszámíthatnánk a SCALAR és OVERLAY modulok különböző paraméterekkel történő egymásutáni alkalmazásával is, e helyett azonban kényelmesebb az IDRISI MCE moduljának alkalmazása, mely a feladatot egy menetben oldja meg.
Az MCE modulnak meg kell adni azokat bájt bináris, egyenlő sávszélességű (0-255) faktor képeket, melyeket korábban pld. a domborzatból, földhasználatból, stb. csináltunk és megadni hozzá az előbb kiszámolt súlyokat.
Az MCE elkészíti a kérdéses cél hasznossági térképét. A hasznossági térképből azonban még ki kell választani a legjobb pixeleket olyan mennyiségben, amilyen mennyiségben szükségünk van rájuk (pld. 5000 ha). Az ehhez szükséges következő lépést a RANK modul hajtja végre, mely növekvő vagy csökkenő sorrendben (1 lesz a legjobb) rangsorolja a pixeleket, és egy olyan képet eredményez, melyben a pixelek értéke egyenlő lesz a rangjukkal. Ezután újra osztályozzuk a képet, az ASSIGN modullal 1-et adunk mindazoknak, melyek megfelelnek és kitöltik a kívánt területet, míg 0-t a többinek.

A több cél - több kritérium típusú feladatokat két nagy csoportba soroljuk. Az első csoport a kiegészítő célok csoportja, melyet az a tény jellemez, hogy a kijelölendő földterület egyidejűlegtöbb célnak is megfeleljen (pld. üdülőövezet és vadrezervátum).
Ennek a feladatnak a megoldását az egy cél - több kritérium esetében alkalmazott lineáris összegzési technika hierarchikus kiterjesztése jelenti. Ez gyakorlatilag azt jelenti, hogy az egyes célok szempontjából kidolgozott hasznossági térképeket úgy tekintjük, mintha faktor osztályzati térképek lennének, meghatározzuk a célok súlyait és alkalmazzuk a 6.1 képletet.

Az esetek többségében egy kiválasztott terület csak egy célra használható, ez a helyzet ha földhasználati tervezést akarunk végrehajtani egy bizonyos területen, például ki akarjuk jelölni a lakó-, ipari- és mezőgazdasági övezeteket az elkövetkező fejlesztési időszakra. A feladat első lépcsőjében célonként külön külön, a fent leírtak szerint, elkészítjük az alkalmassági térképeket. Ha a rangsorolás és a szükséges terület nagyság kijelölése után a kapott területek nem fedik egymást, úgy a feladatot megoldottuk és további lépések nem szükségesek. Rendszerint azonban konfliktus lép fel a különböző területek között, azaz ugyanazt a területet több célból is kijelöltük.
Bizonyos esetekben elérhető az elsőbbségi vagy prioritásos megoldás. Ez a módszer fontossági sorrendbe állítja a célokat. Ezután a RANK modul segítségével kielégíti a legfontosabb célt, majd az első célhoz rendelt pixeleknek 0 értéket ad a RECLASS modullal. A már elfoglalt pixelekkel maszkolja a fontosságilag második alkalmassági térképet, elvégzi a rendezést, kiválasztja a második cél pixeleit, lenullázza azokat, és így folytatja az eljárást amíg a célok el nem fogynak.
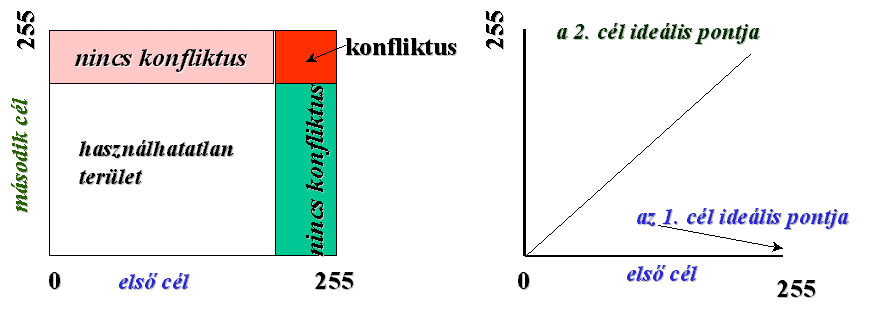
Sokkal használhatóbb azonban a kompromisszum kereséses eljárás mely kényelmes megoldására az IDRISI a MOLA modult kínálja. A modul alapelvét két cél esetére a 6.14 ábra szemlélteti.

6.14 ábra - a MOLA modul működési elvének illusztrációja két cél esetére

Az ábra y tengelyén szerepelnek a második cél, x tengelyén pedig az első cél alkalmassági értékei. A rózsaszín téglalap jelképezi azt a terület részt, mely alkalmas a második cél szempontjából, de nem alkalmas az első cél számára, mivel annak osztályzatai (az x tengelyen látható értékek) túl alacsonyak. A zöld téglalap pedig azt a területet reprezentálja, mely megfelelő az első célnak de nem alkalmas a másodiknak. Ezeken a területeken tehát nincs konfliktus. Nincs konfliktus a fehér téglalap által képviselt területen sem, mivel az egyik célnak sem felel meg. A konfliktus helyzet a piros téglalappal jelzett területen lép fel. Ha meghúzunk a kezdőpontból kiindulva egy 45°-os egyenest, úgy nem nehéz belátni, hogy az egyenes felett ábrázolt pixelek közelebb vannak a kettes cél optimális értékéhez mint az egyes céléhoz, az egyenes alattiaknak pedig az egyes cél ideális értékétől mért távolsága kisebb mint a kettes célétól számított (megjegyezzük, hogyha a célok különböző súlyúak az egyenes dűlése eltér a 45°-tól). A modul tehát úgy működik, hogy az egyenes feletti pixeleket a piros tartományból a kettes célhoz rendeli, míg az egyenes alattiakat az egyes célhoz. Így azonban még nem biztos, hogy a célok területi igényei is kielégítésre kerültek, ezért az eljárás iterációval mindig újabb területeket rendel a fehér zónából a színes zónákhoz mindaddig, míg a területi célokat is sikerül kielégítenie.

A MOLA gyakorlati alkalmazása során meg kell adnunk a célok számát (maximum 15 cél is lehet nem csak kettő mint az ábrán), neveit , relatív súlyukat, a rangsorolt alkalmassági térképek nevét és az egyes célokhoz rendelt terület nagyságot, a területi tűrést és a kimenő kép nevét. Az adatok bevitele után megindul az eljárás és iteratív módon hozzárendeli a célokhoz a megadott területeket.

Az IDRISI döntés támogató képességeinek felvázolásával azt szerettük volna demonstrálni, hogy helyes az az állításunk, miszerint még a téma szempontjából leginkább "kihegyezett" GIS szoftver is csak néhány témában képes a döntéshozásra, nem rendelkezik fejlesztő környezettel, mellyel újabb bonyolultabb modelleket lehetne létrehozni, de talán a legnagyobb hiányosság, hogy hiányzik az a felhasználói interfész, mely lehetővé tenné a dinamikus, interaktív döntés támogatást.

Példák GIS rendszerekbe ágyazott döntéstámogató-modellező alkalmazásokra és fordítottjukra (amikor a modellező rendszerbe ágyaznak grafikus rutinokat)

Talán a hosszú alcím is sejteti, hogy ebben a részben számos alkalmazást tudnánk ismertetni. A terjedelmi és nem utolsó sorban az idő korlátok azonban mértékletességre intenek. Mivel a tematikus alkalmazások során még szándékunkban áll további modellek bemutatása, ezen a helyen csak néhány olyan alkalmazásra térünk ki röviden, melyek a TDR architektúrája szempontjából is érdeklődésre tarthatnak igényt.

A 90-es évek elején M. Batty és Y Xie település fejlődési modellezés kapcsán megvizsgálták a modellező modul és a GIS kapcsolatának két szélső esetét [2], [3].

A szorosan kapcsolt rendszerekben az analitikus és modellező programszegmenseket a GIS keretén belül kódolják a kérdéses GIS fejlesztő nyelvével, mely példánk esetében az Arc/Info makro nyelve az AML.

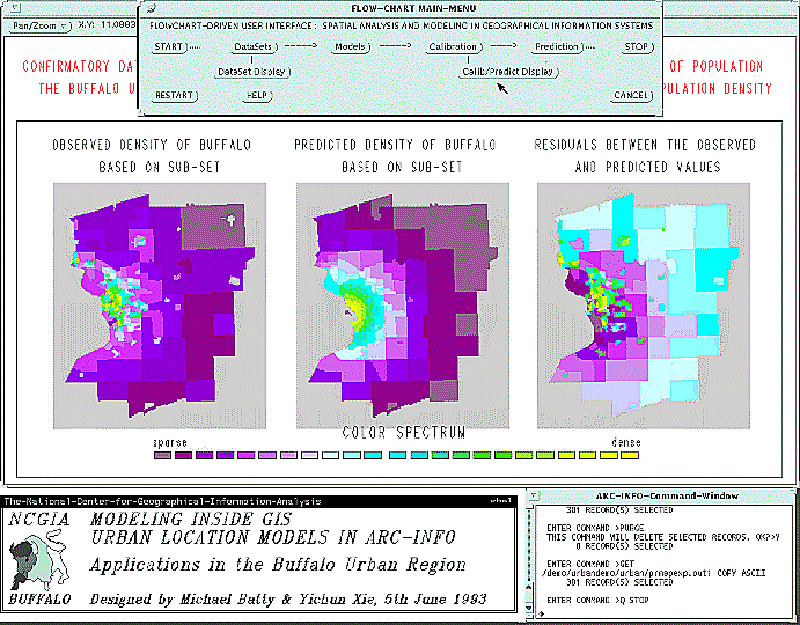
6.15 ábra - Arc/Info-ban létrehozott urbanizációs modell

A felhasználó szempontjából ez a módszer egyenértékű a GIS függvényeinek kiterjesztésével. Ha például a felhasználó lekérdezési módban használja az egeret, úgy a kattintás hatására a GIS megküldi a modellező modulnak a kérdéses hely koordinátáit, mely ennek hatására kiszámolja a kérdéses helyre vonatkozó modell értéket és megjeleníti egy ablakban.

Másik előnye a GIS-be integrált architektúrának a laza kapcsolást jelentősen meghaladó műveleti sebesség.

A módszer fő hátránya a mellett, hogy örökli a GIS statikusságát az, hogy a GIS specifikus fejlesztő nyelven programozott modell csak a kérdéses GIS-ben futtatható. Természetes hátrány az is, hogy a korábban már valamilyen általános programozási nyelven készített és kipróbált modellek ebbe az architektúrába nem illeszthetők bele. A 6.15 ábra példájában, az ábra tetején szerepel a folyamatábra formában létrehozott főmenü, a jobb alsó ablakban az AML parancs ablak, míg középen a Buffaló városi körzet népsűrűsége (bal oldali kép), várható népsűrűsége (középső kép) és a kettő különbsége (jobb oldali kép) látható.

A másik szélső esetben az elemző program külön készül és a GIS-szel csak az adatokon keresztül kommunikál egy vagy két irányban. Két irányú kommunikáció esetén először a felhasználó betölti a kérdéses térbeli fájlt a modellező szoftverbe, majd az az által produkált térbeli modellt megjeleníti a GIS-szel. Egy irányú kommunikáció esetén a modellező szoftver betölti a kijelölt térbeli fájlt, de a megjelenítést is a saját rajzi eszközeivel a GIS-től függetlenül végzi (6.16 ábra). Ez azonban további hátrányokkal is járhat (hacsak a modellező szoftver nem rendelkezik fejlett GIS képességekkel), mivel nemcsak az egérrel végzett lekérdezések válnak lehetetlenné, hanem a zoomolás is, illetve változó földrajzi feltételek esetén, ha például a vizsgált város több kerületre oszlik át kell alakítani a modul grafikus megjelenítését végző program rész kódját.

6.16 ábra - a munkahely és lakóhely kölcsönhatását elemző modell beépített megjelenítő rutinnal

Érdekes megemlíteni, hogy a város és városi környezet fejlődéssel kapcsolatos legújabb modell [4], melyről szóló ismertetés egyelőre a webről is letölthető továbbra is a GIS-szel kiépített laza kapcsolat alapján készült.

A PUP (Projections for Urban Planning = várostervezési vetítések) nevű C nyelven írott modellező program keretét a 6.17 ábrán mutatjuk be (mivel a folyamat ábra jelölései többnyire közismert rövidítések eltekintettünk magyar változata megrajzolásától).

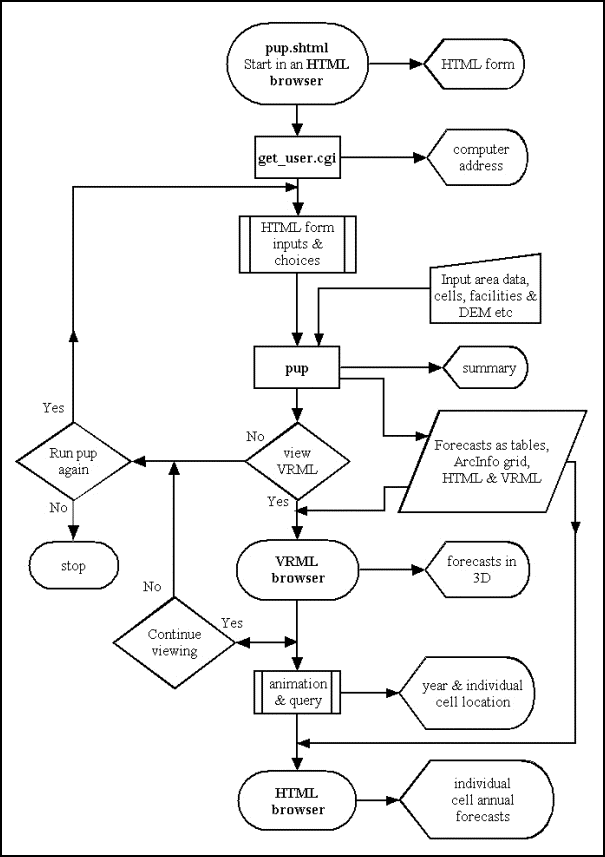
6.17 ábra - a PUP program folyamat ábrája

A program vezérlése a grafikus felhasználói interfészen (GUI) keresztül történik. A felhasználó kitölti a HTML űrlapon a modellezés forgató könyvére vonatkozó paramétereket, melyeket a WEB szerver továbbít az előrejelző programnak. E paraméterek felhasználásával a program beolvassa a térbeli adatokat, elvégzi a kért változók előrejelzését és egy sor output adatot gyárt. A vezérlés ezután visszakerül a HTML űrlaphoz melyen a felhasználó kiválaszthatja, hogy meg akarja-e nézni az eredményeket, vagy pedig új forgatókönyvet kíván futtatni új paraméterekkel.

A C nyelvű program lefordított kódja egy biztonságos WEB szerveren fut. A GUI-nak választott HTML nyelv és fordítói ingyenesek, könnyen kezelhetők és operációs rendszer függetlenek legalább is a tallózót futtató felhasználó számára (ezért is esett a választás a HTML-re), az űrlap működését JavaScript program segíti.

A GIS és a modellező program (PUP) laza kapcsolata úgy realizálódik, hogy az előrejelző program a térbeli bemenő adatokat GIS által készített fájlokból nyeri az eredményeket pedig szintén olyan ASCII táblázatos fájlokba írja ki, melyeket az Arc/Info GRID modulja inputként elfogad. Outputként ezen kívül még VRML (virtual reality modelling language) szkript is készül a megjelenítéshez. A megjelenítés az előzőekből következően VRML kiegészítéssel (pld. CosmoPlayer plug-in) ellátott tallózóban történik (6.18 ábra).

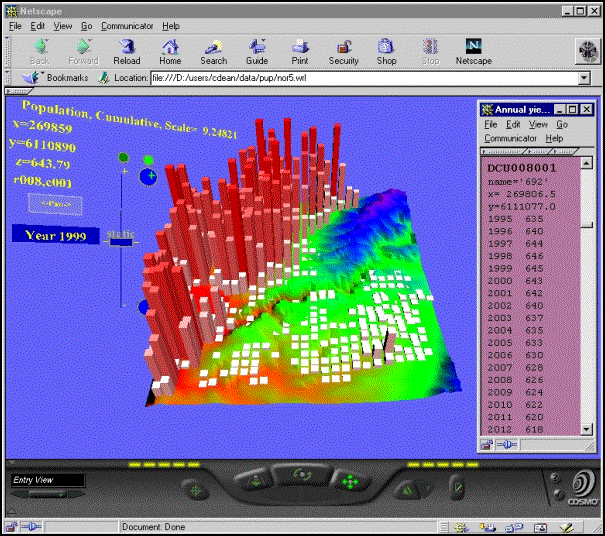
6.18 ábra - az Adelaide városi vonzáskörzet Noarlunga részén várható népsűrűség kiinduló VRML képe az 1999-2020 évekre vetített előrejelzéshez

A VRML tallózó biztosítja az animációt, melyet a PUP outputja kapcsán már említett VRML szkript tesz lehetővé olymódon, hogy olyan gombokat és csúszkákat hoz létre a képen, melyek segítségével a felhasználó változtathatja az animáció sebességét, illetve egyes évekre vonatkozó állóképeket jeleníthet meg. Lehetőség van a 3D-s ábra forgatására, nagyítására, az ábra feletti repülésre, stb. Amint a folyamat ábrából is látható mind a 3D-s, mind a 2D-s változó előrejelzés egyedileg is lekérdezhető adott cellára és évre vonatkozóan. Az Arc/Info GRID formátumú adatok pedig tovább elemzhetők az Arc/Info GRID moduljában.

A figyelmes olvasó valószínűleg észrevette, hogy eddig a fő hangsúlyt a rendszerek felépítésére fordítottuk és nem mélyedtünk el abban, hogy mit, milyen céllal és milyen módszerrel kívánunk modellezni. A következő példánkban, ha kis mértékben is, de eltérünk ettől a tárgyalási módtól és megpróbáljuk felvázolni a modell tartalmi kérdéseit is.

Következő, szintén laza kapcsolatú példánk a szabatos szállítási időpontok meghatározását célozza városi környezetben [5].

Az iparban és a szolgáltatásokban nagy szerepe van az úgy nevezett Időre Érzékeny Szervezésnek (angolul Time-critical logistics = TCL), ami például azt jelenti, hogy a gyártó egység nem alkalmaz raktárkészletet, hanem akkora rendeli az alkatrészeket, amikorra beépítésüket a technológiai folyamat előírja. Talán egyszerűbb, de az egyén számára fontosabb példa, ha azt akarjuk megbecsülni, hogy a 8 órakor induló repülőgéphez mikor kell elindulnunk és milyen úton, ahhoz hogy pontosan érjünk a repülőtérre.

A legtöbb közlekedési út optimalizáló algoritmus vektoros úthálózat rendszerrel dolgozik. Ebben a szervezésben a hálózatot csomópontok és az azokat összekötő szakaszok vagy összeköttetések alkotják.

Ha a forgalom nem befolyásolná az utak áteresztő képességét, akkor ismerve a szakaszokon kifejthető maximális sebességet valamint a szakaszok hosszát kiszámíthatnánk minden szakaszra az áthaladási időt (vagy idő impedanciát) és a Dijsktra algoritmussal meghatározhatnánk egy kiindulási ponttól valamennyi csomópontig a legrövidebb utakat alkotó szakaszokat és a hozzájuk tartozó menetidők utak szerinti összegét.

Úgy gondoljuk, hogy az algoritmus alapelvét legegyszerűbben egy kis példán keresztül érthetjük meg, ezért eltekintünk a formális megfogalmazástól - képleteket írni a WEB oldalra különben sem egyszerű - és a következő 6.3 táblázatban lépésenként illusztráljuk az algoritmus munkáját.

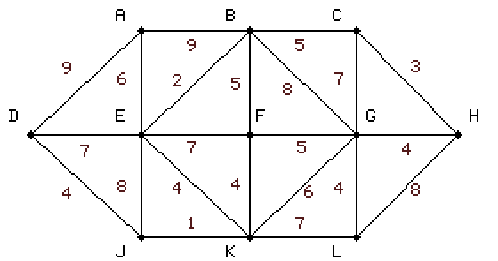
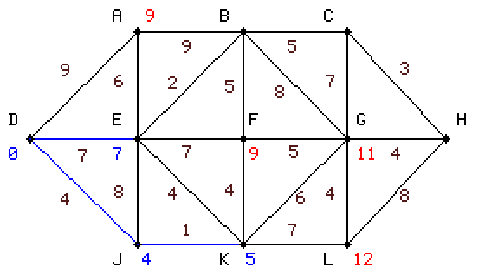
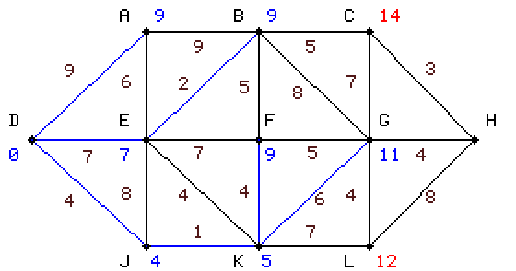
	Ez a kiinduló gráf, a kezdő pont a D, a költségeket barna számok jelölik az élek mellett.
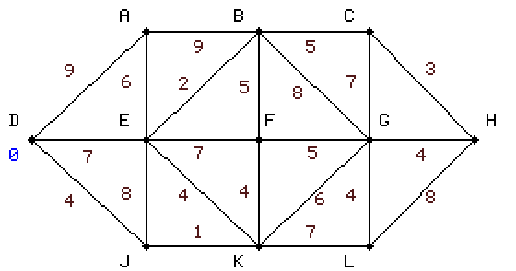
	A nulladik lépésben az algoritmus meghatározza D távolságát saját magától ami természetesen 0. Ezután 10-szer megismétlődik a következő eljárás: megjavítjuk a távolság becslést a választott csúcspont szomszédos csúcspontjaira és kiválasztjuk a D-hez legközelebbi, még kiválasztatlan élet.
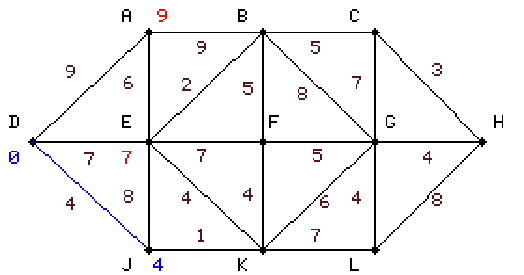
	első lépésben kiszámítjuk A, E, és J távolságát, s mivel az utóbbi a legkisebb kijelöljük a DJ élet és J csúcspontot.
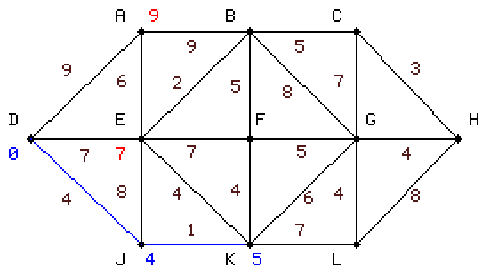
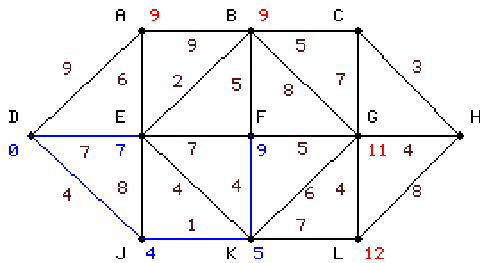
	második lépésben megismételjük most már J-ről a vizsgálatot K-ra és E-re, E-re 12-t kapunk, ez nagyobb mint a meglévő 7 ezért ezt nem változtatjuk, K-ra 5-öt kapunk, ez a J csomópontról szomszédos legkisebb csomóponti érték: bekékítjük.
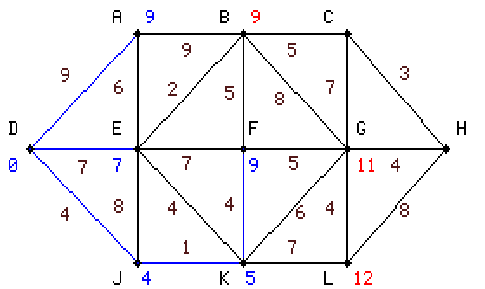
	harmadik lépésben K-ról számoljuk E, F, G, L értékeit. E kivételével a többi értéket pirossal beírjuk, E-nek pedig bekékítjük korábban kapott legkisebb értékét, mivel az összes rendelkezésre álló érték közül ez a legkisebb.
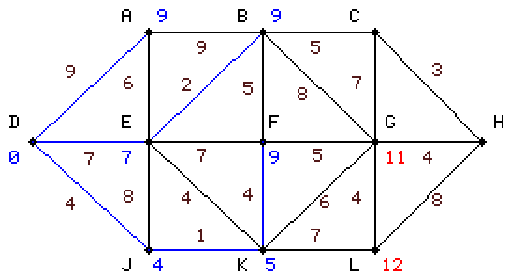
	negyedik lépésünket értelem szerint E-ről kezdjük és kiszámoljuk innen A, B, F értékeit. A-ra, F-re nagyobbat kapunk mint korábban kaptunk ezért meghagyjuk régi értékét, B-re beírunk 9-et és mivel a legkisebb érték három csúcson is 9, bármelyiket választhatjuk a tovább haladáshoz, mi kékítsük be F-et azzal az éllel amivel 9 kijött.
	ötödik lépésünkben F-ről B-t és G-t számítjuk, de mivel nagyobbak a meglévőknél meghagyjuk a piros értékeket. A legkisebb érték most 9 az A-n és B-n, kékítsük be A-t, a 9-et produkáló DA éllel együtt.
	hatodik lépésben A-ból csak B-t tudjuk meghatározni, de ez 18 lenne, tehát meghagyjuk B meglévő 9-ét és mivel ez a legkisebb, bekékítjük a létrehozó EB éllel.
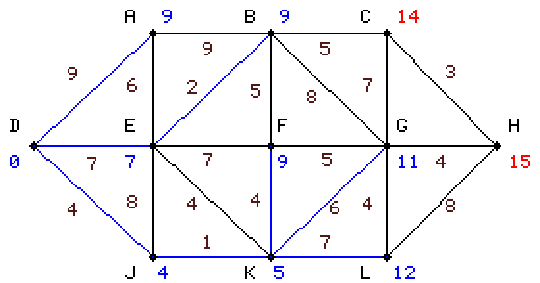
	hetedik lépésben B-ből kiszámoljuk C-t és G-t, G nagyobbra adódik (18) a meglévő 11-nél ezért ezt meghagyjuk, C-hez pedig beírunk 14-et. Mivel a hálózatban legkisebb még nem kék érték a G-n 11, azt bekékítjük a létrehozó KG éllel együtt.
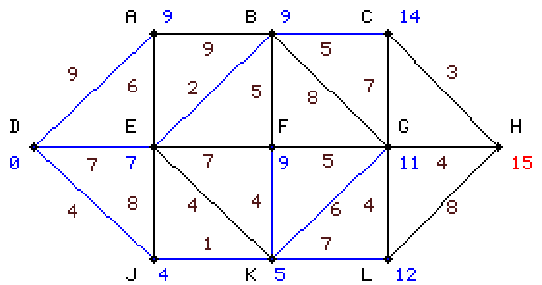
	nyolcadik lépésben G-ről számoljuk C, H és L értékét. H értékét 11 + 4 = 15 beírjuk, C és L nagyobbra adódott a régi értékeknél, ezért azokat megtartjuk. Mivel a legkisebb még nem kék érték L ezt bekékítjük a létrehozó KL éllel együtt.
	kilencedik lépés: L-ből kiszámoljuk H-t, de ez nagyobb a meglévő értéknél ezért azt meghagyjuk, a legkisebb érték 14 a C-n ezért bekékítjük a létrehozó BC éllel együtt.
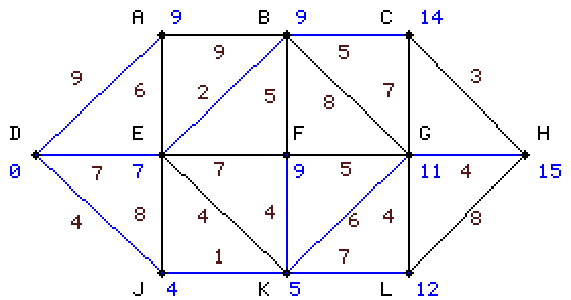
	tizedik lépésben C-ről kiszámítottuk H-t, de nagyobb lett a meglévő értéknél ezért azt meghagytuk. A legkisebb még nem kék érték H-nál 15, ezért ezt bekékítjük a létrehozó GH éllel együtt. A létrejött hálózat kék vonalai megadják D-től a kérdéses csúcsig a legrövidebb topológiát, a csúcsok melletti számok pedig az út hosszát. Természetesen a „hossz” csak választott mérőszám, mely lehet költség, idő, komfort, és más felhasználási tényező is.

6.3 táblázat - egyszerű hálózati példa a Dijkstra algoritmus működésére

Mivel azonban az utak telítettsége befolyásolja az útszakaszokon történő áthaladás idejét elvileg minden időpillanatban más és más lehet az optimális út. A tárgyalt modell annak a dinamikus forgalmi egyensúlyi helyzetnek a modellezésére vállalkozik, melyben a résztvevő járművek útvonaluk megváltoztatásával már nem javíthatnak utazási ráfordításukon (nem csökkenthetik a cél elérésére fordított időt).

A dinamikus forgalom modellezésnél vizsgálhatjuk a forgalmi helyzetet az idő folyamatos függvényeként vagy diszkrét időintervallumokban. A folyamatos idejű rendszerek a forgalom áramlást a dinamikus rendszer optimális vezérlése megoldásának tekintik. Ez a felfogás a jelentős számítási erőforrás mellett folyamatos idejű forgalom monitorozást igényel bemenő adatként. Alkalmazása az intelligens gépjármű navigációs rendszerekben indokolt a megfelelően kialakított figyelő rendszer megléte esetén.

Az általunk ismertetett rendszer gyakorlati szállítás szervezési alkalmazásokat kíván széleskörűen kiszolgálni, ezért viszonylag egyszerű hardveren alkalmazható és az időfüggő terheléseket forgalomszámlálások általánosítására támaszkodva határozza meg. Ezeket a feltételeket az úgynevezett dinamikus felhasználó optimális megközelítés (dynamic user optimal = DUO) biztosítja, mely időben diszkrét dinamikus áramlási modell s mint ilyen elvileg tetszőleges felbontású idő-szakaszok áramlási képét modellezi.

A DUO elv állítása szerint hálózati egyensúly esetén egy, azonos időintervallumban elindult jármű sem csökkentheti menetidejét útvonala egyoldalú megváltoztatásával. Amint látjuk tehát az eredetileg kitűzött cél a megvalósított modellben annyiban módosult, hogy az optimalitás az egy időintervallumban elindultakra korlátozódik.

A menetidő minimalizálási feladat korlátozásai részben a hálózat topológiája és attribútumai részben az időbeni Kezdőpont-Célpont (angolul O-D) mátrixok alapján írhatók fel. A mátrixoknak rendelkezésre kell állniuk minden, általában 5-10 perces intervallumra a vizsgálati időtartományban, mely naponta néhány órát jelent.

A modellező szoftver az adatokon keresztül kapcsolódik a GIS szoftverhez. Az ismertetett kísérleti szoftverben a modellező programot Visual C++ 5. verzióban írták, GIS szoftverként pedig az Arc/Info 7.1.2. verzióját használták. A bemenő adatokat Arc/Info fedvényekként (coverage) kell a GIS-ben létrehozni. Az úthálózatot olyan ARC típusú fedvény képviseli, melyben a szakaszok (ezt hívják arc-nak vagy link-nek) rendelkeznek azokkal az attribútumokkal, melyek a szakasz menetideje meghatározásához szükségesek például a következő képlet felhasználásával:

T = T₀·[1 + a₁·(Q / C_S)^a2],      (6.2)

ahol:
T = a szakasz megtételéhez szükséges utazási idő;
T₀ = a szakasz megtételéhez szükséges utazási idő szabad áramlás esetén;
Q = szakasz áramlási arányszám gépkocsik száma / időintervallum;
C_S = a szakasz stabil állapotú kapacitása (gépkocsi szám / időintervallum)-ban kifejezve;
a₁, a₂ = empirikus paraméterek.

Az empirikus paramétereket városonként érdemes meghatározni. Csak példaként mutatjuk be a₁ és a₂ értékeit a kanadai Winnipeg városára:

megengedett sebesség (mérföld/óra)	a1	a2
0 - 30	1.50	4.42
31 - 40	1.03	5.52
41- 50	1.01	6.59
50+	1.15	6.87

6.4 táblázat - tapasztalati paraméterek a menetidő képlethez a kanadai Winnipegből

A kezdőpont-cél mátrixokat POINT (pont) típusú fedvények formájában szintén a GIS-ben kell létrehozni. Minden kezdő és cél ponthoz a koordinátákon kívül valamennyi olyan pont megnevezése is tartozik az attribútum táblázatban, ahova a kérdéses pontból útvonalak indulnak ki. Fontos megemlíteni, hogy ezek a mátrixok minden intervallumra (5-10 perc) külön készülnek. Ha a városi hatóságok a forgalom számlálások során rögzítik az indulási időt és a célt, úgy a mátrixok létrehozásának semmi elvi akadálya sincs. Ha azonban a K-C értékek csak egész napra összesítve állnak rendelkezésünkre, úgy azok lebontására rendszerint a napi áramlási profil görbét használják, a diszaggregálás részleteire itt nem térünk ki.

A modellező szoftver az attribútumokat tartalmazó INFO fájlokat olvassa, illetve a vizsgálat eredményeit új INFO fájlokba írja, minden vizsgált időintervallumról egy új fájl készül. Ezek a fájlok megjeleníthetők és elemezhetők az Arc/Info-ban. Ha megadjuk a kezdő és végpontot valamint az indulási időt a GIS függvény a modellező program által gyártott INFO fájl felhasználásával kiszámítja a menetidőt és megrajzolja az optimális utat. Ezzel a módszerrel csak iterációval lehet meghatározni a szükséges indulási időpontot. A szoftver tovább fejlesztése során olyan eljárást is ki akarnak dolgozni, mely explicit módon megadja, hogy mikor kell elindulni adott érkezési időponthoz.

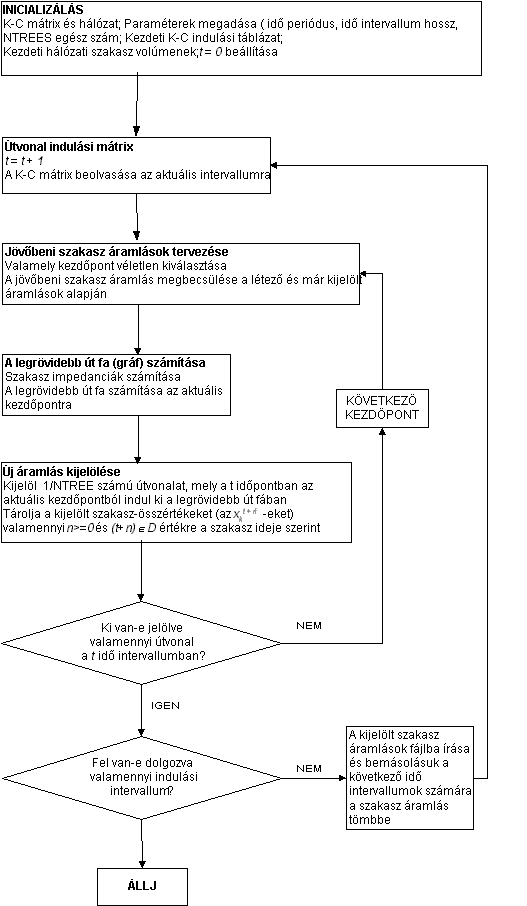
A modellező program működését a 6.19 ábrán bemutatott folyamatábrával szemléltetjük.

6.19 ábra - a DTA forgalom modellező szoftver folyamat ábrája

Amint a folyamat ábrából is látható az inicializálás után a program kiválaszt egy kiinduló pontot és megbecsüli az innen kiinduló szakaszokon a forgalom áramlás értékét a korábbi és jelenlegi intervallumban már kijelölt terhelések alapján. Ezután kiszámítja a szakaszok idő impedanciáját és meghatározza a kérdéses kiinduló pontból az összes célpontba vezető legrövidebb utat a Dijkstra algoritmussal.
Ezután megvizsgálja, hogy a kérdéses csomópontból induló útvonalak mely szakaszokat mikorra és mennyire terhelik és így kialakítja a jelenlegi és jövőben megvalósuló áramlási képet. Végig haladva az összes kiinduló ponton valamennyi útvonalra elvégzi a szakaszokhoz történő terhelés hozzárendelést. A célból hogy e hozzárendelés ne véletlenszerűen következzen be egy kezdőpontról egy időintervallumban kiinduló útvonalak kiválasztásakor az útvonalakat a program NTREES (egész szám, a kísérletben az értéke 3 volt) részre osztja és ezeket a részeket rendeli az ugyancsak NTREES számú legrövidebb út fa egyikéhez. Ezt a ciklust kell ezután minden kiindulópontra és minden időintervallumra megismételni.

Mielőtt bemutatnánk az első eredményeket ábrázoló képeket megjegyezzük, hogy a szerzők kifejtették az irányú eltökéltségüket, hogy létrehozzák a rendszer GIS-szel szorosan összekapcsolt változatát, valamint, hogy elkövetkező fejlesztésükben szabatos optimalizáló algoritmust alkalmaznak, mivel a jelenlegi algoritmus szerény környezet igényének az az ára, hogy csak közelítő optimumot szolgáltat.

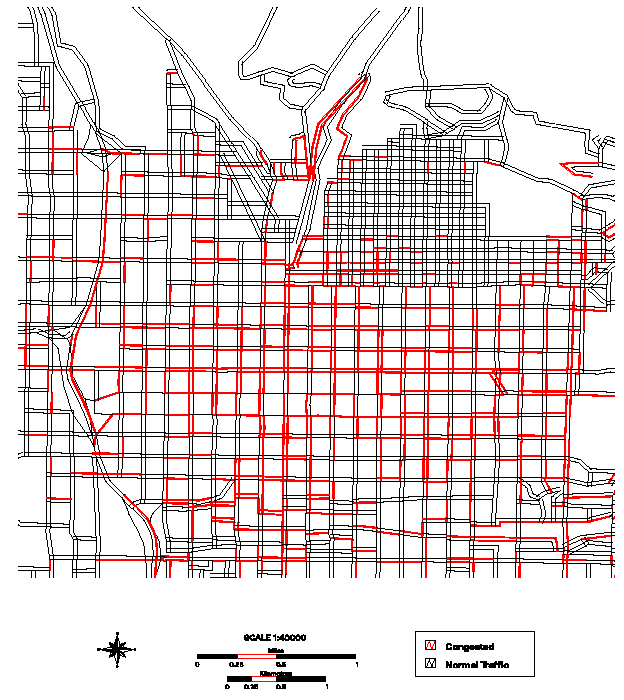
6.20 ábra - Salt Lake City úthálózat torlódási mintája az 1. időintervallumban, a piros szín jelzi a torlódásokat, fekete a normális forgalmat

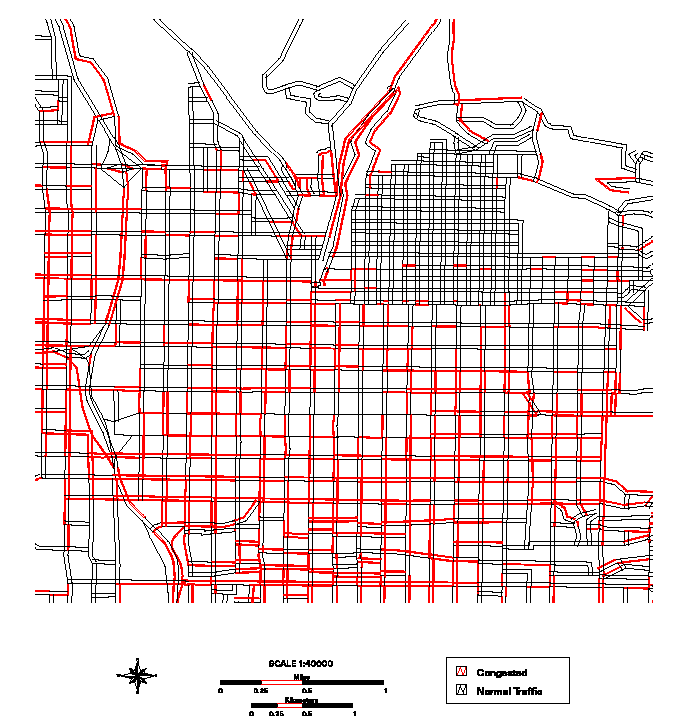
6.21 ábra - Salt Lake City úthálózat torlódási mintája az 13. időintervallumban, a piros szín jelzi a torlódásokat, fekete a normális forgalmat

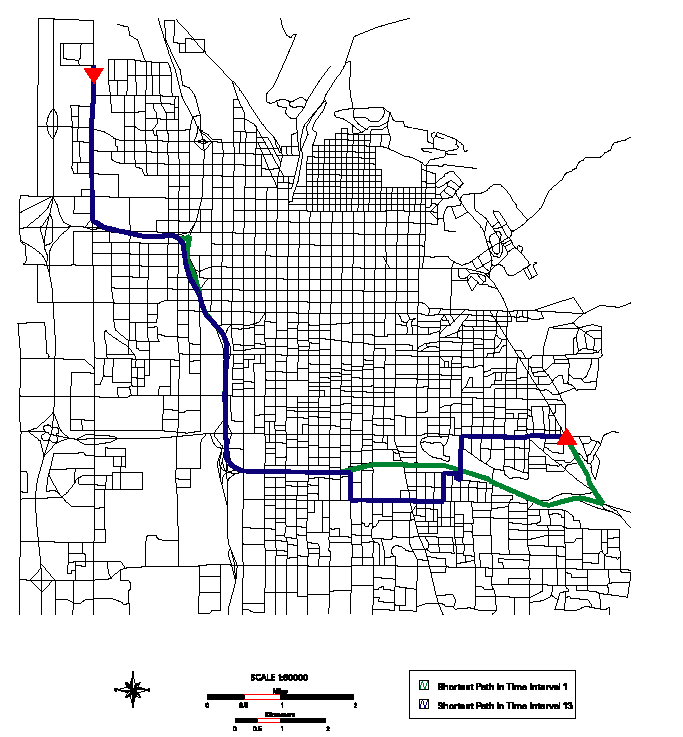
6.22 ábra - legrövidebb utazási idejű útvonalak az 1. (zöld vonal) és 13. (kék vonal) időintervallumban

Összetett rendszerekkel realizált döntéstámogató rendszerek

Az IDLAMS (The Integrated Dynamic Landscape Analyzis and Modeling System = Integrált Dinamikus Táj-Elemző és Modellező Rendszer) és OO-IDLAMS (OO = Objektum Orientált) Rendszer [6].

Az IDLAMS katonai megrendelésre készült, kidolgozásában az Argonne Nemzeti Kutató Laboratóriumon kívül még részt vet az USA Hadsereg ERDC-CERL rövidítésű kutató-fejlesztő központja is.

A rendszer alapvető feladata az volt, hogy segítsen olyan döntéseket hozni, melyek maximalizálják a hadsereg gyakorló terepeinek kihasználtságát, de emellett gondoskodnak arról is, hogy az ökológiai egyensúly a kérdéses gyakorló terepeken és környékükön ne boruljon fel.

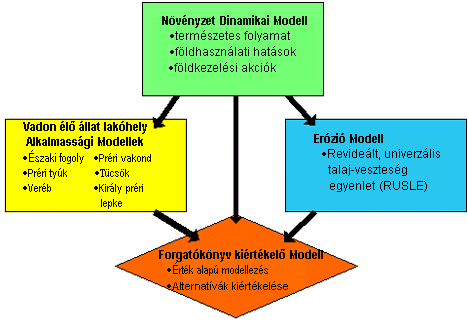
Az IDLAMS kidolgozását 1994-ben kezdték. Abból indultak ki, hogy GIS DSS generátorral kapcsolják össze a növényzet dinamikai , erózió, vadon élő állatok lakóhely alkalmassági modelljeit a kiértékelő-optimalizáló modullal. A rendszer architektúráját a 6.23 ábrán vázoljuk fel. Meg kell említeni, hogy több napos irodalom búvárkodás eredményeképpen sem sikerült kideríteni, hogy milyen GIS-t használ a rendszer. Egy web-lap töredéken arra találtam utalást, hogy telepítéskor azt a raszteres GIS-t kell alkalmazni, mely az intézménynél jelenleg is üzemel. Ebből arra a következtetésre jutottam, hogy a rendszerben a GIS szervező szerepe a térbeli adatokon keresztül realizálódik, olymódon, hogy az IDLAMS főmodulja (a vegetációs modul) több GIS formátumot is elfogad illetve generál.

6.23 ábra - az IDLAMS rendszer diagramja

A rendszer főmodulja meghatározza azokat a növényzet változásokat, melyek a természeti folyamat, a földhasználat változás illetve a föld kezelésével kapcsolatos műveletek eredményei. A modul által generált térképek képezik a bemenetet a többi modul számára. Az élőlények lakókörzetének alkalmasságát vizsgáló modul az USA Halászati és Vadon Élő Állatok Szolgálatának alkalmassági indexeit alkalmazza a bemenő, tényleges állapotot tükröző vagy szimulált felszínborítást/növényzetet ábrázoló rétegekre. Bizonyos állatfajok kiegészítő bemeneti térképeket is igényelhetnek. Az eróziós modellnek a valós vagy szimulált növényzeti/felszínborítási rétegeken kívül más olyan térbeli adat rétegekre is szüksége van, melyek befolyásolják az eróziót. Az ökológiai modelleket a forgatókönyv kiértékelő modul kapcsolja az üzemeltető igényeihez. Ez a modul valósítja meg interaktív módon az alkalmazási variánsok között a kompromisszumot.

Az IDLAMS-szal végzett döntés-előkészítések alapján 1998-ban meghatározták a rendszer továbbfejlesztésének főbb követelményeit:

1. Adaptívabb és rugalmasabb mechanizmusra van szükség a szétszórtan működő alkalmazói szoftverek integrálására;
2. Fokozottabban kell tudni figyelembe venni az ökoszisztéma, földhasználat, és földkezelési gyakorlat dinamikáját;
3. Támogatni kell az olyan szoftver alkalmazásokat, melyek többszörös térbeli és időbeli skálán képesek dolgozni;
4. Csökkenteni kell a modellezési technológia hosszú távú költségeit a meglévő adatok, modellek, rendszer komponensek ismételt felhasználásával.

A kitűzött cél megvalósítását úgy kívánták elérni, hogy az IDLAMS rendszert az objektum orientált DIAS keret rendszerbe integrálták.

Mivel az OO IDLAMS célja elsősorban az objektum orientált keretszoftver hasznosságának igazolása nem pedig egy komplett döntés támogató rendszer felépítése volt, ezért az eredeti IDLAMS moduloknak csak egy részét vitték át az új rendszerbe, mégpedig a Növényzeti Dinamika Modellt és a Henslow féle veréb lakóhely modellt. Figyelembe véve a DIAS lehetőségeit, a katonai gyakorlatra és földhasználatra vonatkozó akció komponenseket, melyek korábban a növényzeti modell részei voltak kivették ebből a modellből és úgy nevezett akció objektumokként (COA) implementálták a DIAS-ban. A COA objektum úgy tekinthető, mint egy procedurális vagy szekvenciális folyamat folyamat-ábrája. Mind a három egyszerű, a prototípusban realizált akció objektum: a "gyakorlatozik", az "éget" és az "ültet" procedurális jellegű és könnyen implementálható a DIAS-ban.

Az OO-IDLAMS entitás objektumai tartalmazzák azokat az állapot változókat, melyek a modell együttes be-, és kimeneti paramétereit képviselik. Hasonlóképpen ezekbe az objektumokba helyeződnek el a modell együttes által implementált "viselkedés" formák (tulajdonképpen, hagyományos kifejezéssel eljárás hívások).

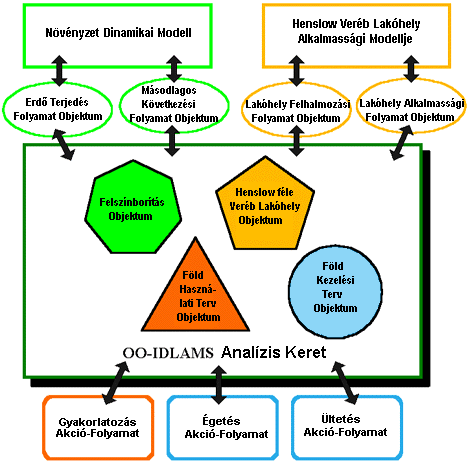
Az új verzió illusztrálását tartalmazza a 6.24 ábra.

6.24 ábra - az OO-IDLAMS prototípus architektúrája

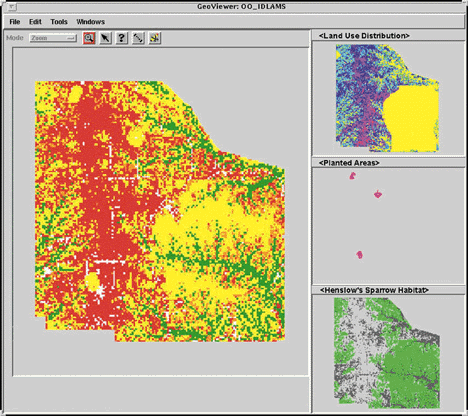
A GIS funkciókat a DIAS-szal kapcsolatban már említett Geo Viewer nevű objektum orientált GIS modul realizálja. Ezzel a modullal lehet navigálni a vizsgálati területen, lekérdezéseket kezdeményezni, objektumokat manipulálni, új nézeteket nyitni, stb. A szimulációk során megjeleníthetők a különböző időpontoknak megfelelő kimeneti paraméterek. A 6.25 ábra négy külön nézetben jelentkező paramétere: a felszínborítás, földhasználati beosztás, beültetett területek és a veréb számára alkalmas lakóterület.

6.25 ábra - az OO-IDLAMS földrajzi megjelenítése a GIS modullal

A DIAS architektúra két előnyére is érdemes felhívni a figyelmet. Az entitás objektumokban elhelyezett viselkedés formák a külső modellek eljárásait aktiválják. Például a Felszínborítás objektum "implementáld a természetes folyamatot" nevű viselkedése meghívja a természetes növény változási folyamatot a Növényzet Dinamikai Modellből, hasonlóképpen az "implementáld az erdő terjedési folyamatot" nevű viselkedés az erdő terjedési rutint indítja el ugyanebből a modellből. Ha azonban más algoritmussal akarjuk modellezni a kérdéses folyamatokat úgy új külső modellt illeszthetünk a DIAS kerethez anélkül, hogy a program többi részét, a többi modellekkel fennálló kapcsolatokat meg kellene változtatnunk. Természetesen, ha az új modell más input/output paraméterekkel rendelkezik, úgy a megfelelő entitás objektum paraméter rendszerét át kell alakítanunk. Az első előny tehát az új külső modellek csatlakoztatási lehetősége a rendszer egyéb részeinek változatlanul hagyásával.

A másik előny a modellek közötti futás idejű visszacsatolás lehetősége. A kialakított prototípusban ilyen visszacsatolásra a Henslow féle Veréb Lakóhely Modell és a Föld Használat Terv Objektum által meghívott Telepít akció folyamat között lehetséges. A Henslow féle Veréb Lakóhely Modell akkor minősíti a különben megkívánt növényzettel borított foltokat kiválónak, ha legalább 65 ha méretűek. Ha a kapott foltok környezetében őshonos növényzetet telepítünk, kielégítve a megkívánt területi feltételt, úgy jelentősen segítjük az állatfaj életkörülményeit. A visszacsatolás úgy realizálódik, hogy minden idő lépésben az Ültet akció folyamat lekérdezi a Henslow féle Veréb Objektum foltok és kiegészítő hektárok kellenek nevű attribútumának aktuális értékét. Ez meghívja a Henslow féle Veréb Lakóhely Modell-nek azt a folyamatát mely kiváló tulajdonságú lakóhely foltokat alakít ki. Az Ültet akció folyamat megvizsgálja, hogy találhatók-e a kiválasztott foltok mellett károsított füves területek, melyeken a fű újra telepíthető a területi korlátozás igényeinek megfelelően. 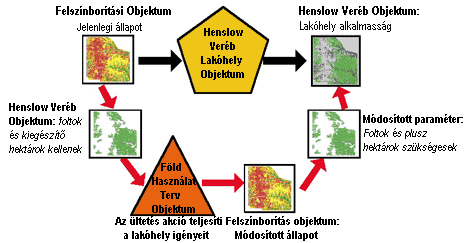Ha a lehetőség fennáll, úgy a rendszer kialakítja a 65 hektáros foltokat és kijelöli a füvesítendő részeket. A visszacsatolás folyamatát a 6.26 ábra illusztrálja.

6.26 ábra - modellek közötti dinamikus visszacsatolás az OO-IDLAMS-ban

Az OO-IDLAMS példája jól bizonyítja, hogy a korszerű modellező és döntéstámogató rendszereket objektum orientált technológián alapuló keretszoftverekre támaszkodva célszerű megvalósítani.

Integrált Tervezési Döntéstámogató rendszer (IPDSS) [7]

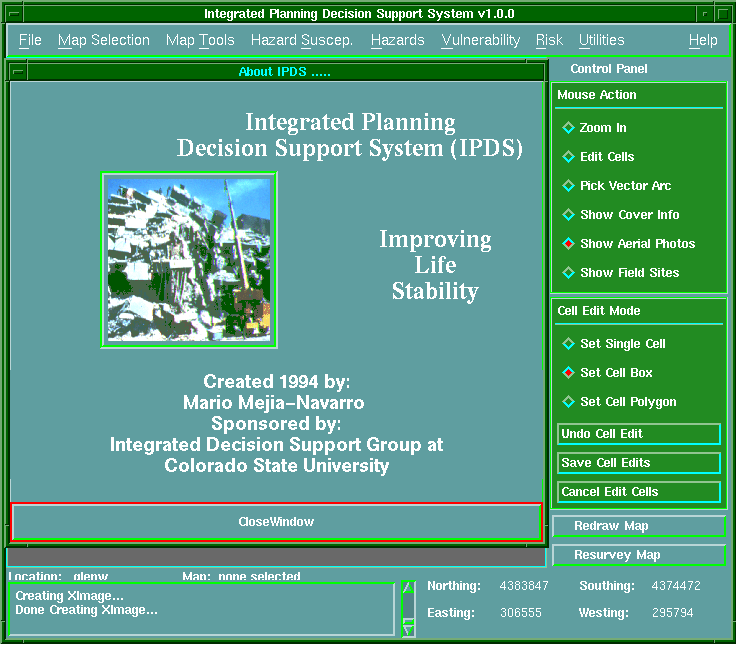
Az Integrált Tervezési Döntéstámogató Rendszer IPDSS, geológiai, környezeti veszélyek figyelembevételére és az ennek megfelelő földhasználat tervezés támogatására készült Colorádó Állam Egyetemén 1994-ben. A kor követelményeinek megfelelően a rendszer önálló szoftvereket kapcsol az adatok segítségével össze és tesz elérhetővé a szabványos elemekből felépített grafikus felhasználói interfészen keresztül. A rendszer fő interfész kezelő ablakát a 6.27 ábrán mutatjuk be.

6.27 ábra - az IPDSS rendszer fő interfész kezelő ablaka

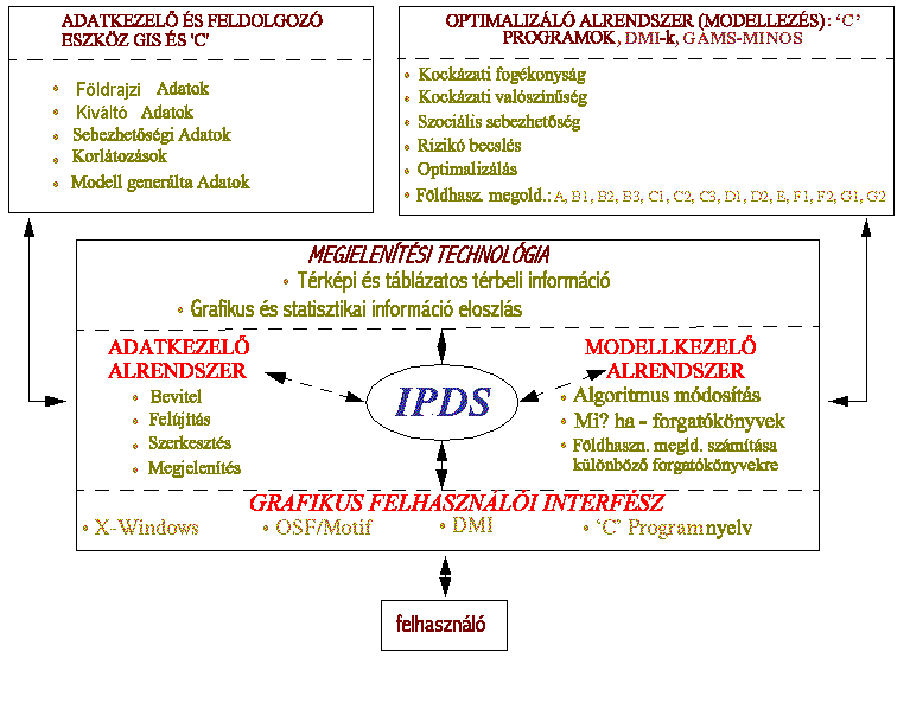
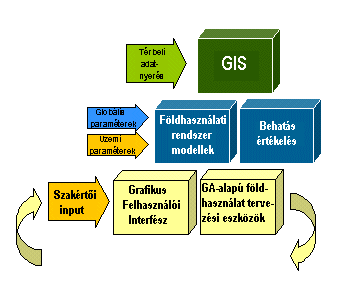
Az IPDSS főbb részei (6.28 ábra):

• Az Adatkezelő Rendszer (DMS), feladata az adat gyűjtés, transzformáció, megjelenítés. GIS eszközöket igényel ezért a feladatra az ingyenes és C nyelven fejleszthető GRASS GIS-t alkalmazták a rendszer megalkotói. A DMS lényegében olyan intelligens könyvtár mely rengeteg vészhelyzet vonatkozású elemző adatot tárol.
• A Modell Kezelő Rendszer (MMS) adatelemző modelleket kezel, emulálja a folyó elemző eljárást, numerikusan modellez és eredményeket szolgáltat.
• A GUI, melyet szabványos UNIX elemekből (X-Windows, OSF/Motif) állítottak össze ablak, menü, ikon és párbeszéd ablak vezérelt.

Ha új modellező programot akarunk kapcsolatba hozni a GIS által kezelt és megjelenített adatokkal úgy a két szoftver között kapcsoló programot kel írni. Ezt a feladatot teljesíti a GUI részét képező "C" programozó interfész, mely segítségével dinamikus kapcsolat biztosítható az MMS modellektől a DMS-hez, úgy hogy a GIS mint adatbázis forrás szerepel a vezérlő program felé.

6.28 ábra - az IPDSS rendszer fő alkotó elemei

A rendszer eredeti kiépítésében a geológiai jellegű veszélyforrások modellezésére, a veszélyforrásokkal szembeni emberi és anyagi sebezhetőség értékelésére és a fentieket figyelembe vevő többkritériumos földhasználati tervezésre készült.

A témához felhasznált adatok többek közt: a topográfia, lejtőirány, mély és felszíni geológia, strukturális geológia, geomorfológia, talajok (geotechnikai adatok), felszínborítás, földhasználat, hidrológia, szociológia, csapadék (éves átlag és várható maximum), áradási térképek, és történelmi adatok a veszélybecslésre.

A megbecsülendő veszélyek: sárfolyások, süllyedés, esetleges egyéb veszélyek a maximális várható csapadék és szeizmicitás hatására.

A sebezhetőségi vizsgálatok:

1. az ökoszisztéma érzékenységére,
2. a gazdasági sebezhetőségre és
3. a szociális infrastruktúra sebezhetőségére vonatkoznak.

A kiértékelési-tervezési munka során a felhasználó

• megegyezésre jut a tervezési döntéshozásban figyelembe veendő kritériumokról;
• adatokat gyűjt a kritériumra és a GIS-szel adatbázist épít;
• elméleti és történelmi információk alapján módosítja az inputot;
• kiszámolja és kategorizálja az összes korlátozást, beleértve a trigger (kirobbantó) feltételeket is;
• támogatja az algoritmusok megvitatását.

A továbbiakban villantsuk fel egy-két vonással és ábrával a rendszer néhány fontos tulajdonságát.

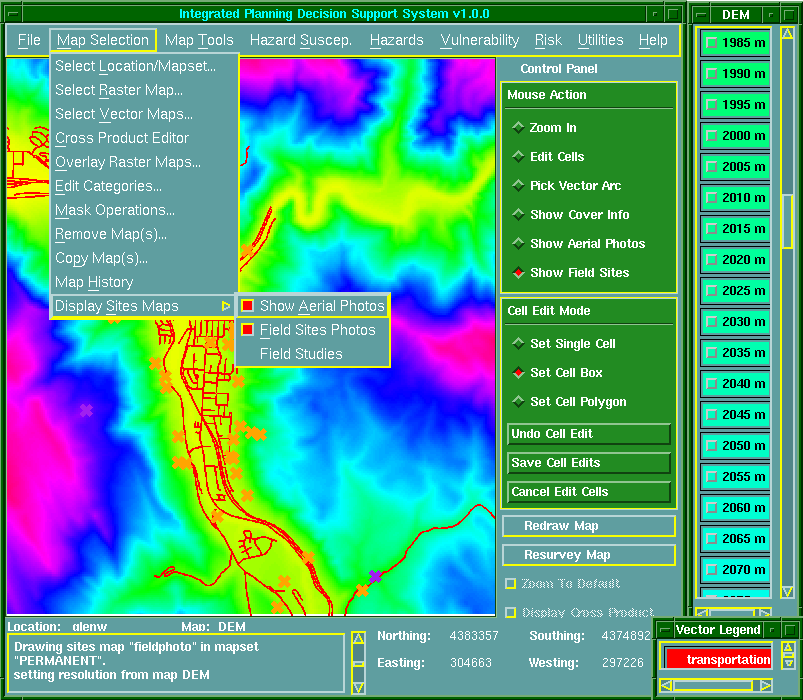
A rendszer, hála az alkalmazott GRASS GIS-nek kiváló térinformatikai képességekkel rendelkezik (6.29 ábra):

• alkalmas raszter és vektor térképek, kompozitok megjelenítésére;
• térkép kombinációk létrehozására mivel az IPDSS-nek overlay editora van a kombinációk végrehajtására, melyek használhatók a forgatókönyvekben;
• a Cross-Product Editor megakadályozza az olyan szerkesztéseket, melyek konfliktust hoznak létre a kezelési célokkal;
• ezen kívül funkciói közé tartozik még a területszámítás, zoom, szerkesztés és a légifénykép elemzés.

6.29 ábra - magassági raszter térkép átfedve a közlekedési útvonalak vektor fedvényével és a légi és földi fényképek helyeivel

Az IPDSS-t színes SUN/SPARC-munkaállomáson implementálták, UNIX operációs rendszer és X Window System alatt.

A rendszer első funkciója a veszély források becslése. Az alap kiépítés a süllyedések és sárfolyások becslésére alkalmas, de más kockázat becslő modellek, például áradás, sziklaomlás, földcsuszamlás is kezelhető ugyanezzel az interfésszel.

A bemenő adatok a következők:

• Fogékonyság, melyet fizikai faktorok kombinációja determinál, olyanok mint a domborzat, felszíni geológia, tektonika, geomorfológia, talaj típus, geotechnika, növényzet, földhasználat és felszín borítás, hidrológia, szociológia, stb.
• Kirobbantó (angolul trigger = ravasz) faktorok, melyek a szeizmikusság, csapadék és földhasználat kombinációjából adódnak .

Minden faktornak kiszámolják a befolyási indexét minden helyre egy specifikus súllyal. Ezeknek az értékeknek a szorzásával és összegzésével meghatározzák a relatív veszélyt:

VESZÉLY = VESZÉLY_FOGÉKONYSÉG*TRIGGER(T)

Ezért a sárfolyás veszélye (Hdf) nem más mint a sárfolyás veszély fogékonyság (Sdf) megszorozva a trigger faktorokkal, mely vagy a csapadék (Tdf_p), szeizmikusság (Tdf_s), vagy a kettő kombinációja (Tdf_ps).

Hdf = Sdf*[Tdf_p | Tdf_s | Tdf_ps]        (6.3)

A veszély fogékonyságot befolyásoló természeti tényezők mérnöki tevékenységgel módosíthatók a terepen. A módosítások súlyozva vihetők be a rendszerbe. A 6.30 ábrán az érzékenységet mint a befolyásoló faktorok súlyozott összegét láthatjuk, mely interaktívan módosítható.

6.30 ábra - veszély fogékonyság szerkeszthető algoritmusa

Sdf = ((slopedf * (aspect*7 + usc_casag*4 + sgmdf*9 + veg*8 + hgdf*5 + shrswell1*2 + erosK*7 + lusess*3 + wsbuf1*8 + femahist2*10 + isohyaa*4)/67) + 9)/10           (6.4)

A képletben szereplő változók az alábbi faktorok valamely értékéhez rendelt osztályzatok (részletes meghatározásukat, és hogy milyen értéknél milyen osztályzatot kapnak az érdeklődők megtalálják [7]-ben):

• slopdf - lejtő szög,
• aspect - lejtő irány,
• usc_casag - kőzet mállás,
• sgmdf - a lejtőt borító geológiai képződmény folyás érzékenysége,
• veg - növényborítási index,
• hgdf - hidrológiai talajcsoport,
• shrswell - agyagtartalom,
• erosK - talajeróziós potenciál,
• lusses - földhasználat zónák,
• femahist2 - történelmi sárfolyások,
• isohyaa - csapadék.

A wsbuf1 jelentése nem szerepel a cikkben, valószínűleg valamilyen védő-övezettől függő érték.

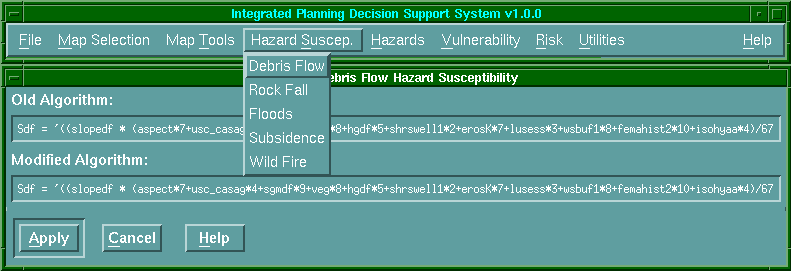
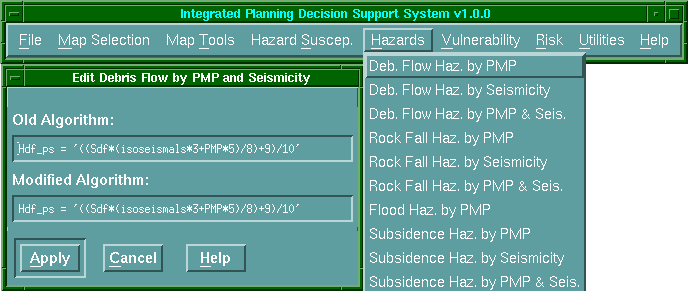
Az IPDSS interfész úgy készült, hogy a felhasználó a trigger faktorokat közvetlenül a "Hazard" lehúzós menüben alkalmazhatja a kérdéses veszélyre kattintva.

Az eredmény interaktívan nyerhető, a használót érdeklő gomb megnyomásával (pld. "Debris Flow Hazard" azaz sárfolyás az eső (PMP) és szeizmikusság trigger faktorokkal) mely aktiválja a panel bal oldalán beírt képlettel kifejezett modellt (6.31 ábra).

6.31 ábra - lehúzható "veszély" menü a trigger faktorokkal

A sebezhetőség algoritmusa a befolyásoló tényezők és a szociális jellemzők válaszának relatív értékelésével készül.

A földhasználati sebezhetőség (luseV) értékelése a települési infrastruktúra (épület típus és anyagok, gazdasági zónák), városi infrastruktúra (csatornázás, védekezési építő munkák), szociális infrastruktúra (kulturális feltételek) figyelembe vételével készül.
A lakók sűrűsége (human_density) a népszámlálási tömb/ember adaton illetve az elemzés minimális cella méretén alapul.
A fő kommunikációk (lifelines) faktora figyelembe veszi a vonalak köré vont védőövezeteket.

vulnerability = (human_density*10 + luseV*7 + lifelines*2)/19           (6.5)

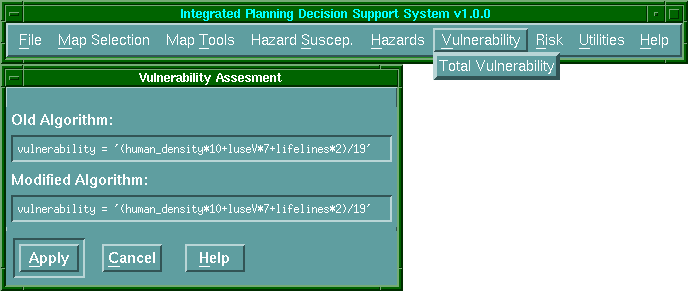
Az IPDS a „sebezhetőség” ("Vulnerability") lehúzható menüvel biztosítja, hogy a felhasználó módosítsa a sebezhetőségi meggondolásokat, beszúrva a véleményét az új algoritmusba, mely képes számolni a városi infrastruktúra, települési infrastruktúra és kulturális infrastruktúra sebezhetőségének kombinációját (6.32 ábra).

6.32 ábra - lehúzható "sebezhetőség" menü

A kockázatbecslés a legfontosabb célja a városi tervezési döntéseknek, mivel magába foglalja az emberek és városi infrastruktúra sebezhetőségét valamely esemény előfordulásának valószínűsége alapján.
A lakókörnyezetre vonatkozó kockázati információ különösen komplett eszköze a kockázati övezet térkép.
A specifikus kockázati (Rei) övezetesítés olyan eljárás, mely zónákra bontja a régiót valamely specifikus veszélyforrásnak (sárfolyás, áradás, sziklaomlás, süllyedés) való kitettség (Hi) szempontjából.
A térkép jelentősége abban van, hogy segítségével megítélhető a jövőben várható veszélyek helye, valószínűsége, és relatív komolysága ezzel a potenciális veszteségek megbecsülhetők illetve megfelelő intézkedésekkel csökkenthetők vagy elkerülhetők.

Rei = f(Hi, Ve).          (6.6)

A kockázati övezetek célja a tervezési folyamatban:

1. az okozó tényezők redukálása,
2. a sebezhetőség redukálása és
3. a fizikai, gazdasági, mentális károsodás csökkentése.

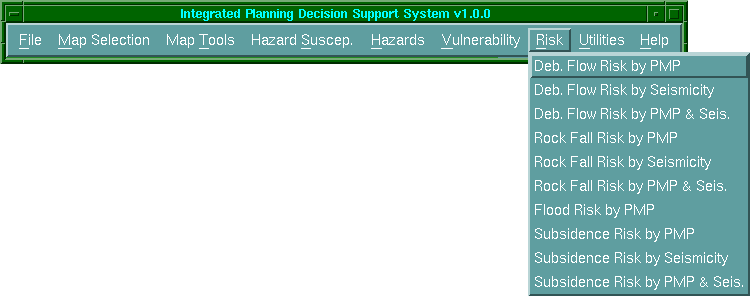
A "Risk" lehúzós menü lehetővé teszi azon potenciális károk földrajzi eloszlásának szelektív kiértékelését, melyek károsíthatják azokat a szociális jellemzőket, melyeket a felhasználó különböző veszély fajta sebezhetőségi számításánál választ (6.33 ábra).

6.33 ábra - lehúzható "kockázati" menü a kockázati forgatókönyvek szelektív becslésére.

A LADSS (Land Allocation Decision Support System = Föld Hozzárendelési Döntés Támogató Rendszer) rendszer

A rendszert a Skócia-i Macaulay Földhasználati Kutató Intézet fejlesztette ki a falusi földhasználat tervezés támogatására [8]. A multidő talán nem teljesen helyes mivel a rendszer kipróbálása és továbbfejlesztése jelenleg is folyamatban van.

A rendszer ismertetésével elsődlegesen az a célunk, hogy betekintést nyerjünk egy eredeti optimalizálási eljárás együttes - a genetikus algoritmusok világába is.

Amint már erről többször szóltunk, a GIS és az optimalizáló szoftver kapcsolata alapulhat a közös adat formátumon (ilyen rendszer volt például a szabatos szállítási időpont meghatározását végző közlekedési rendszer), amikor a lényegében különálló szoftverek ugyanazokat a fájlokat írják és olvassák, vagy lehetnek teljesen integráltak mint a DIAS alkalmazások.

A LADSS közbenső utat választott: az optimalizáló-tervező program modulok és a GIS mint különálló programok egy szekvenciális adatátvitelt és távoli rutin hívást realizáló "BRIDGE" (HÍD) nevű szoftvermodul segítségével kapcsolódnak egymáshoz, de közös grafikus felhasználói interfésszel rendelkeznek. Már itt megjegyezzük, hogy mind a HÍD, mind a GUI, mind az optimalizáló rendszer a G2 nevű fejlesztő környezetében került kialakításra. A rendszer komponenseit a 6.34 ábrán mutatjuk be, mely a már hivatkozott [8] cikkre támaszkodva készült.

6.34 ábra - a LADSS komponensei

A rendszer GIS komponenseként az objektum orientált Smallworld GIS-t alkalmazták a rendszer tervezői. Bár ez a rendszer nálunk nem nagyon ismert, a megadott linkből kiderül, hogy széleskörűen alkalmazzák közmű információs rendszerek kiépítésére.

A földhasználati döntésekhez szükséges térbeli adatstruktúra négy hierarchikusan egymásba ágyazott, különböző feldolgozási méretaránynak megfelelő objektum osztályt definiál:

• az üzem szintű osztály az alapja az egész gazdaság auditálásának az üzemelési feltételek elemzése alapján. Ez a méretarány teszi lehetővé a művelési egységek költségvetési táblázatainak vizsgálatát, a szükséges munkaerő felhasználás elemzését valamint a művelési ágak hatásának figyelembe vételét az egész gazdaság talajkonzervációs értékére;
• a táblák az azonos művelésű terület egységek, melyekhez a földhasználatot a tervezési eszközök hozzárendelik;
• a tábla részlet a táblának biológiai, fizikai, talajtani szempontból még homogénnek tekinthető része;
• a tábla részlet poligon a tábla részlet geometriai leírása.

A rendszer térbeli adatmodellje tehát, ellentétben a legtöbb földhasználat modellező szoftverrel, nem raszteres, hanem tulajdonképpen vektoros, ami pontosság szempontjából mindenképpen kompromisszumokra kényszeríti a szoftver használóit. Ez a kompromisszum akkor indokolt, ha összhangba hozható a tényleges adatnyerési pontossággal. Érdemes megemlíteni, hogy maga az objektum orientáltság nem határozza meg, hogy vektoros vagy raszteres-e a koncepcionális térbeli adatmodell, csak az implementációs modellt definiálja. A legújabb irodalomban [9] részletes leírást találhatunk arra, hogy miként implementálják objektumként a raszter cellát.

Visszatérve a tábla részletek attribútumaira, az eredeti térbeli adatok (topográfia, talaj jellemzők, stb.) mint rács pontok kerülnek rögzítésre a rendszerben. A tervezési feladatok végrehajtásakor a tervezési modulok megkerestetik a GIS-szel a tábla részletekbe eső adatpontokat és a tábla részlet attribútumait a beeső pontok attribútumainak átlagolásával határozzák meg. A módszer előnye, hogy ily módon az adatok frissítése, vagy új adatforrások (pld. gyakorlati szakemberek tapasztalatai) bevonása csak új pontok bevitelét vagy a régi pontok módosítását igényli, de nincs szükség az objektum attribútumok átírására, mivel azt a kiértékelés során maga a program végzi.

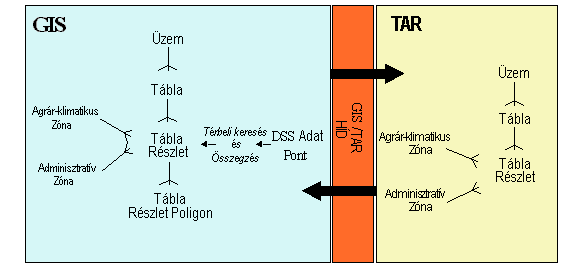
A térbeli objektumok a GIS mellett részleges tükrözéssel a feldolgozó-optimalizáló Tudás Alapú Rendszerben (TAR) is tárolásra kerülnek. Erre az ismételt tárolásra elvileg nem volna szükség, elég volna az objektumok neveit a TAR-ban rögzíteni és a szükséges attribútumokat a GIS-ből lekérni, ha a két rendszer közötti kommunikáció gyorsabb és megbízhatóbb lenne. Úgy látszik azonban hogy a GIS és TAR közötti HÍD (BRIDGE) szoftver ezekkel a jellemzőkkel nem rendelkezik ezért a részbeni duplikált tárolás indokolt lehet. A rendszer adatstruktúráját a 6.35 ábrán vázoltuk fel.

6.35 ábra - a LADSS adatstruktúrája

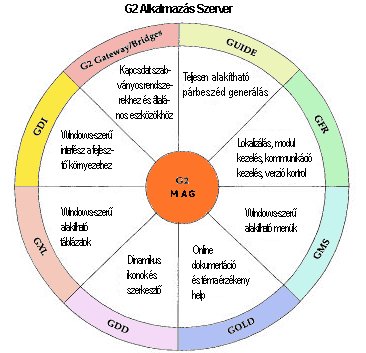
A földhasználati modulokat tavaszi árpára, réten tartott felföldi birkára és tejtermelő tehénre, öt lombos és két tűlevelű fa fajtára dolgozták ki. Valamennyi esetben a modulokat procedurális szoftverként a Gensym cég G2 nevű tudás alapú fejlesztő környezetében dolgozták ki. A G2 rendszerrel kapcsolatban megemlítjük, hogy objektum orientált rendszerről van szó, mely lehetővé teszi, hogy a fejlesztők a tudást objektumok, szabályok, módszerek és eljárások segítségével reprezentálják grafika és strukturált természetes nyelv felhasználásával. A G2 segédprogramjai (6.36 ábra) többek közt lehetővé teszik a már többször hivatkozott HÍD programok vagy felhasználói interfészek egyszerű elkészítését.

6.35 ábra - a G2 segédprogramjai

A földhasználati modulok publikált modellek alapján valamennyi földhasználat esetén hasonlóan működnek. Először meghatározzák a kérdéses táblarészlet alkalmasságát a kérdéses földhasználatra. Az ehhez szükséges attribútum adatokat, amint már említettük, a GIS-ből veszik. Ezután, ha a terület alkalmas meghatározzák a produktivitást (tonna/ha a gabonára, maximális állatsűrűség a téli takarmány figyelembe vételével, köbméter/ha a fa fajták esetén) az agronómus által megadott művelési rendszernek megfelelően. Végül kiszámolják a földhasználat jövedelmezőségét a globális paraméterekként megadott árak függvényében. A fenti vizsgálatok tábla részlet szinten történnek, és az eredmények jelentős része bemenő adatként jelentkezik a hatás elemzéshez.

A hatás elemző modulok a gazdasági, szociális és természeti hatások vizsgálatát hajtják végre. A legjobban kidolgozott gazdasági modul a földhasználati modulok outputjából (a hektáronkénti nyereségből = bevétel - kiadás a munkabér és tőke költség figyelembe vétele nélkül) kiszámolja a művelési egység "nettó jelenlegi értékét", figyelembe véve az esetleges jutalmakat és szubvenciókat (a felhasználó által meghatározott időbeli széthúzással). A szociális behatást kezelő komponens elsősorban a foglalkoztatás nagyságát, típusát és időbeli eloszlását méri, a környezeti indexeket pedig most készülnek kifejleszteni a GIS-ben, elsőként olyan táj morfológiai mutatókat sorát számolva mint például a kerület/terület arányok.

A grafikus felhasználói interfészt a G2 környezet segédprogramjai segítségével alakították ki, ez azonban nem akadályozza, hogy az interfészből, tehát a G2-ből a HID-on keresztül küldött módszer hívással manipuláljuk például a GIS felhasználói menü rendszerét.

A földhasználati tervezési eszközök lehetővé teszik, hogy a gazdaságok irányítói bevigyék a rendszerbe a cél(oka)t, azaz, hogy mely hatás elemző modul(oaka)t jelölnek meg az optimalizálás alapjául, továbbá a globális, üzemi és pénzügyi paramétereket (pld. a szubvenciót az árpa termelésre), a rendszer pedig megkeresi, hogy a táblákon optimális esetben milyen földhasználat legyen. A többes számot azért tettem zárójelbe, mivel a rendszer elvileg több cél alapján is képes keresni, a hivatkozott cikk illetve WEB lap azonban részletesebben csak az egy cél szerinti kereséssel foglalkozik. Ezért a továbbiakban mi is ezt nézzük meg részletesebben és tárgyalásunk végén térünk rá a több cél szerinti optimum keresés néhány specifikumára.

A rendszer optimalizálásra a Genetikus Algoritmust (GA) használja, s mivel ez a technika nem túl régi, s egyben nagyon sok területen eredményesebben használható a hagyományos technikáknál érdemes lesz az alapelvével röviden megismerkednünk. Az érdeklődők figyelmét felhívjuk Marek Obitko cseh egyetemi hallgató 1998-ban készült angol nyelvű oktató anyagára, mely a témát röviden és világosan foglalja össze, s e mellett JAVA appletekkel demonstrálja az algoritmus működését. Megjegyezzük még, hogy néhány ábránkat a hivatkozott anyagból magyarítottuk.

A Genetikus Algoritmus (GA) az élővilág Darwin által fölfedezett törzsfejlődését modellezi. A megoldandó problémákat a módszer vektorokként modellezi. Egy véletlen vektor populációt (egyszerűbben bizonyos számú véletlen vektort) kell létrehozni, és összehasonlítani a problémával. Az összehasonlítás eredményeképpen a vektoroknak jósági értéket kell adni annak megfelelően, hogy milyen jól oldják meg a problémát. Ezután a rossz (alacsony jósági számú) vektorokat törlik az állományból és a maradékból új állományt hoznak létre a reprodukció keresztezés és mutáció műveleteivel. A folyamat mindaddig folytatódik amíg a megadott jósági szintet el nem érjük, illetve amíg egy meghatározott lépésszámban sem lehet jobb vektort létrehozni.

A témával kapcsolatban gyakran használt Genetikus Programozás olyan genetikus algoritmus, mely vektorokként kifejezésekből álló fákat használ. A kifejezésekből álló fákat arra használja, hogy egyenletet fejlesszen ki a probléma megoldására. A Genetikus Programozás gyakran használja a LISP programozási nyelvet, mivel ebben a nyelvben igen egyszerű a kifejezésekből álló fák felírása. E kis kitérő után folytassuk a genetikus algoritmus tárgyalását, mivel a LADSS ezt és nem a GP-t használja az optimalizálási feladat megoldására.

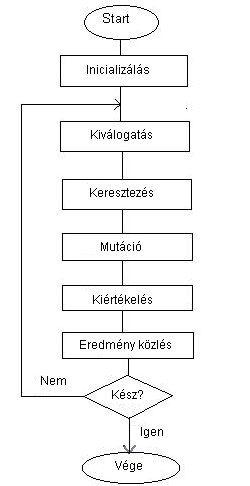
A folyamatábránál kissé részletesebben szövegben kifejtve a genetikus algoritmus a következő lépésekből áll: [Start] Olyan n kromoszómából álló véletlen populáció generálása (melyek alkalmasak a probléma megoldására). [Jóság (angolul fitness)] A populáció valamennyi x kromoszómája f(x) jósági értékének kiszámítása. [Új populáció] Új populáció létrehozása az alábbi lépések mindaddig történő ismétlésével, amíg az új populáció nem válik teljessé. [Kiválasztás] Két szülő kromoszóma kiválasztása a populációból jóságuknak megfelelően (minél jobb a jóság annál nagyobb az esélye egy kromoszóma kiválasztásának). [Keresztezés] A keresztezési valószínűséggel a szülők keresztezésével utódok létrehozása. Ha nem történik keresztezés az utódok a szülők pontos másolatai. [Mutáció] A mutációs valószínűséggel az utódok létrehozása az egyes gének (a kromoszóma vektor elemeinek) megváltoztatásával (mutálásával). [Elfogadás] Új utód elhelyezése az új populációban. [Kicserélés] Az újonnan létrehozott populáció használata az algoritmus további futása során. [Tesztelés] Ha teljesül a megadott végfeltétel az algoritmus megáll és kiírja a legjobb megoldást az aktuális populációban. [Hurok] Ha a feltétel nem teljesül folytatás a 2. lépésnél.

6.36 ábra - a GA folyamatábrája

A populáció n kromoszómából áll, míg a kromoszómák vektorok lévén elemekből, melyeket géneknek hívunk. A gének rendszerint nem maguk a lehetséges megoldás vektorok, hanem azoknak a konkrét feladattól függő kódjai. A lényeg az, hogy a gének lehetőleg egyszerűen legyenek kezelhetők, de ennek ellenére alkalmasak legyenek az általuk reprezentált megoldás vektorok jósági értékeinek kiszámítására.

A populációban lévő kromoszómák számát a működő rendszerek 20-100 között szokták megválasztani (a nagyobb szám finomabb felbontást de lassabb működést eredményezhet).

A kromoszómák kódolására a következő főbb sémákat alkalmazzák:

• bináris kódolás esetén a gének a 0 vagy 1 értékeit vehetik fel, azaz például a következőképpen nézhet ki egy kromoszóma:

1

0

1

1

0

0

1

1

1

0

• a permutációs kódolás azt jelenti, hogy a kromoszómát olyan számokból álló sztring alkotja, mely kifejezi a kérdéses számok egymásutánját valamely rendezési folyamatban. Például, ha a gének olyan útszakaszokat jelentenek, melyek összekapcsolnak két kijelölt pontot, úgy a

4

7

10

5

3

2

1

8

9

6

• kromoszóma azt jelenti hogy az általa képviselt megoldásban először a négy sorszámú útszakaszon kell végigmennünk, utána a hét sorszámún, a tíz sorszámún, stb.
• Az érték szerinti kódolás esetén a gének a keresési térben lévő megoldás vektorok elemeinek értékeit veszik fel, melyek számok vagy karakterek lehetnek. Ha például a szóba jöhető földhasználatokat az abc kis betűivel jelöljük, a gének sorszámát (a vektor elemek indexét) pedig a táblákhoz kapcsoljuk, akkor a

b

a

c

d

f

i

j

e

g

h

• kromoszóma egy olyan megoldást képvisel, melyben az első táblához a b földhasználat (pld. fenyő erdő), a kettes táblához az a földhasználat (pld. lombos erdő), a hármas táblához c földhasználat (pld. tavaszi árpa), stb. tartozik.
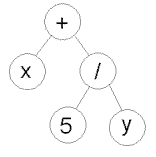
• A teljesség kedvéért megemlítjük a fa kódolást is, mely elsősorban a genetikus algoritmus programfejlesztésre használt változatában - a genetikus programozásban használatos. Ez a kódolás a kromoszómákat műveleti fákból vagy program lépésekből építi fel. Mi az előbbire mutatunk be egy egyszerű példát:

( + x ( / 5 y ) )

• a második sorban található a kromoszóma fa által reprezentált művelet csoport matematikai leírása.

A populáció létrehozása után a genetikus algoritmus kiszámolja valamennyi kromoszóma jósági értékét. A jósági függvények a konkrét alkalmazástól függnek. Az általunk vizsgált mezőgazdasági döntéstámogatási rendszerben például a jósági értékeket a hatáselemző modulok számolják. Ha például a gazdasági hatáselemző modul megkapja, hogy az első táblán fenyő erdő földhasználatot tervezünk akkor kiszámítja az ebből a földhasználatból a konkrét tulajdonságokkal rendelkező táblára eső nettó jelenlegi értéket. Ezt a számítást elvégzi a kromoszóma valamennyi génjére és a jósági értékek összegzéséből kialakul az adott kromoszóma jósági értéke.

Az új populáció kialakítása ezek után a következőképpen megy végbe. Kiválasztják azokat a legjobb kromoszómákat, melyek változatlanul tovább élnek az új populációban (ezt nevezik elitizmusnak). A maradék kromoszómákból kiválasztják azokat a legjobbakat, melyeket keresztezni fognak és az így létrejövő utódok kerülnek az új populációba. Elvégzik a mutációt és a mutált kromoszómákat beviszik az új populációba. Elhagyják az új populációból a fölösleges, alacsony jóságú kromoszómákat.

Ezt az általános menetet a konkrét algoritmus paraméterezése vezérli. Meg kell adni, hogy az állomány hány %-a legyen a keresztezésből származó utód, hány százalékán hajtsák végre a mutációt, milyen százalékban (vagy jósági index alapján) történjen a változatlan kromoszómák kijelölése, és azt is meg kell határozni, hogy a változatlan egyedek részt vehetnek-e a keresztezésben, illetve, hogy a keresztezést és mutációt egymástól függetlenül vagy egymás után hajtják-e végre.

A kiválogatás (szelekció) ezután mind a változatlanul átadott, mind a keresztezésre kiválasztott kromoszómák vonatkozásában az alábbi sémák valamelyikével történhet:

• a rulett kerék módszer esetén képzik a jósági számok összegét majd generálnak egy véletlen számot a 0 - [összeg] tartományban és megnézik, hogy a szám melyik kromoszóma jósági értékre esik, és azt választják ki, majd a véletlen szám generálástól kezdve ismétlik az eljárást. Tulajdonképpen ez a számítás analóg azzal mintha a 6.37 ábra szerint egy kördiagramba felraknák a jósági értékeket és egy rulett golyót dobnának a forgó körre.

6.37 ábra - rulett kerék választás

• A módszer hátránya egyszerű szemléletből látható a 6.38 ábra példáján: ha nagyon nagy a különbség a legjobb és a többi jósági érték között igen kicsi a valószínűsége, hogy a kisebb jósági értékű kromoszómák is kiválasztásra kerüljenek.

6.38 ábra - rulett kerék választás olyan esetben amikor a legnagyobb jósági érték jelentősen eltér a többitől

• A fenti esetben célszerűbb használni a rangsorolásos keresési módszert. A módszer lényege (lsd. 3.39 ábra), hogy a kromoszómák jósági értékét egyenlővé tesszük az eredeti jósági értékek fordított rangsorában elfoglalt helyükkel, bár a továbbiak egyértelműsége érdekében meg kell jegyeznünk, hogy gyakran a célfüggvényt minimalizálni kell, ilyen esetekben természetesen a legkisebb célfüggvény értékek a legjobbak a rangsor szerinti keresésnél is. A 6.38 ábra példájából tehát úgy vezethető le a 6.39 ábrán bemutatott rulett kerék, hogy a legrosszabb 4. kromoszóma 1 jósági értéket kap, a jóság szerint eggyel jobb 3. kromoszóma új jósági értéke 2 lesz, a második legjobb 2. kromoszóma rangsor szerinti jósági értéke 3, végül a legjobb 1. kromoszóma jósági értéke 4 lesz. Általánosságban tehát N kromoszóma esetén a legjobb kromoszóma rang szerinti jósági értéke N lesz. Annak a valószínűsége pedig, hogy a kérdéses kromoszóma kerül kiválasztásra

p[%] = [rangsor szerinti jóság] *100 / ((N+1)*(N/2)).          (6.7)

6.39 ábra - a 6.38 ábrán bemutatott jósági rulett kerék transzformálása rangsor szerinti jósági értékeket tartalmazó rulett kerékbe

A rang szerinti jóság hozzárendelés tovább finomítható a szelektív hangsúly ( SP = selective pressure) nevű súlyozási paraméter bevezetésével. Tételezzük fel, hogy kromoszómák úgy vannak rangsorolva, hogy a legkisebb jóságú sorszáma (rangsorban elfoglalt helyzete) Ssz az egyes, a legnagyobbé pedig az N. Akkor

Lineáris rangsorolás esetén: a rang szerinti

Jóság(Ssz) = 2 - SP + 2·(SP - 1)·(Ssz - 1) / (N - 1).          (6.8)

Fordított rangsorolás esetén, tehát ha a legrosszabb jóságú van az első helyen a legjobb pedig a legnagyobb sorszámú N.-ik helyen, úgy a rang szerinti:

Jóság(Ssz) = 2 - SP + 2·(SP - 1)·(N - Ssz) / (N - 1).          (6.9)

Az SP érték 1 és 2 között változhat.

A valószínűség értékére az utóbbi két kifejezés felhasználása esetén azt kapjuk, hogy p(Ssz) = Jóság(Ssz) / N.

Ezek után a keresés az eredeti rulett módszer szerint hajtható végre: generálunk egy véletlen számot 0 és 1 között és azt a kromoszómát választjuk ki amelyik rang szerinti, valószínűségben kifejezett jósági területére esik a véletlen szám (ha a véletlen számot 0 és 1 közt generáljuk a valószínűséget természetesen nem %-ban kell kifejezni). Jegyezzük meg, hogy a LADSS is a rang szerinti kiválasztást használja.

A keresztezés és a mutáció az új generáció létrehozásának legfontosabb műveletei. A keresztezési valószínűség és a mutációs valószínűség nevű paraméterek mondják meg, hogy a kérdéses alkalmazás esetén a populáció hány százaléka hoz létre keresztezéssel utódokat, illetve, hogy az állomány hány százaléka megy keresztül mutáción. A szelekcióval kapcsolatban már említettük, hogy a keresztezésre a nagy jósági értékkel rendelkező kromoszómákat kell kiválasztani.

A két művelet konkrét végrehajtása függ a kromoszómák kódolásától, illetve a konkrét alkalmazástól. A számtalan lehetséges módszer közül csak néhányat mutatunk be, melyeket a LADSS rendszer esetében is használnak.

Bináris és érték szerinti kódolásnál

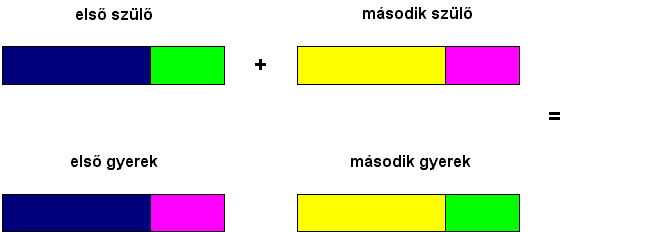
• az egy pontos keresztezést a 6.40 ábrán szemléltetjük. Egy az alkalmazás által megadott pont (általában a felező pont) két részre bontja mind a két szülő kromoszómát, az utódok pedig az így nyert négy részből két-két olyan különböző részből alakulnak ki, mely két rész egyke az első szülőtől, másika a második szülőtől származik.

6.40 ábra - egy pontos keresztezés bináris és érték szerinti kódolás esetén

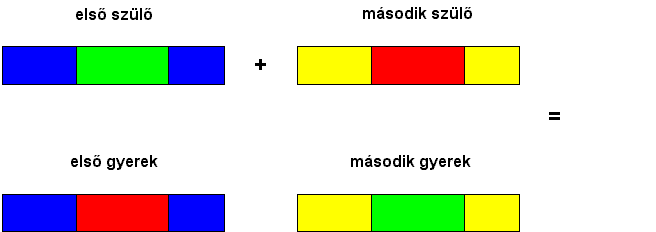
• két pontos keresztezés esetén a két szülő három-három részre bontódik fel az alkalmazás paramétereként megadott pontokon és az utódok az egyik szülőtől két részt a másik szülőtől egy részt örökölnek (6.41 ábra).

6.41 ábra - két pontos keresztezés bináris és érték szerinti kódolás esetén

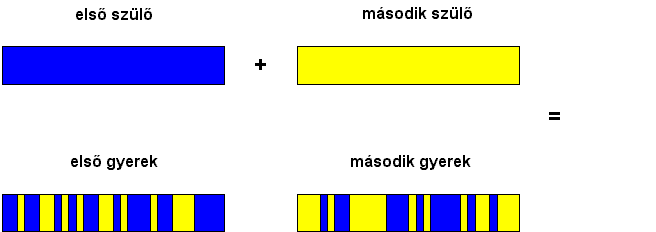
• egyenletes (uniform) keresztezés során a leszármazott kromoszómák génjei véletlenszerűen származnak az egyik vagy a másik szülőtől ( a 6.42 ábra tanulsága szerint egymás mellett több azonos szülőtől származó gén is elhelyezkedhet).

6.42 ábra - egyenletes keresztezés bináris és érték szerinti kódolás esetén

• A mutációt rendszerint az utódok egy kis százalékára alkalmazzák azzal a céllal, hogy az algoritmus ne álljon le valamely lokális szélsőértéknél, hanem közelítsen a globális optimumhoz. Bináris kódolás esetén a művelet abból áll, hogy előre megadott számú gént invertál, azaz ha a gén 0 volt átalakítja 1-re, ha 1 akkor 0-ra. Szimbolikus érték szerint kódoláskor több átalakítási lehetőség van (n szimbólum esetén (n-1)), ezért itt a meglévő szimbólumon kívüliek közül véletlen szerűen választ egyet és azt írja be a meglévő helyére.

A bemutatott lépéseken keresztül új és új populációkat gyárt az eljárás mindaddig, amíg az utolsó generáció átlagos jósága el nem ér egy előre megadott értéket. Ennek a populációnak a legjobb kromoszómája szolgáltatja a megoldás vektort. A keresés azonban a legjobb esetben is csak egy cél szerinti optimumot szolgáltat. Ha több cél optimális kielégítése a célunk, úgy a módszer csak akkor használható, ha technikai továbbfejlesztését megelőzően új elvi meggondolásokat is bevezetünk.

A többcélú optimalizálás

a Pareto féle optimum helyek megkeresésén alapul. Vilfredo Pareto (1848-1923) olasz szociológus és közgazdász, a Lusanne-i egyetem politikai gazdaságtan tanára 1896-97-ben kiadott Politikai Gazdaságtan Tankönyvében fogalmazta meg az összemérhetetlen és esetenként ellentétes célokra irányuló optimalizálás fogalmát. A meghatározás szerint létezik a megengedett megoldás vektoroknak egy olyan felülete (két dimenziós esetben - görbéje) melyen haladva az egyik cél eredményessége csak úgy javítható, ha a többi célok eredményessége csökken. Ez a felület a Pareto felület illetve kétdimenziós esetben a Pareto görbe. Ha a vektorok helyett az eredményességet ábrázoljuk akkor a Pareto frontról beszélünk.

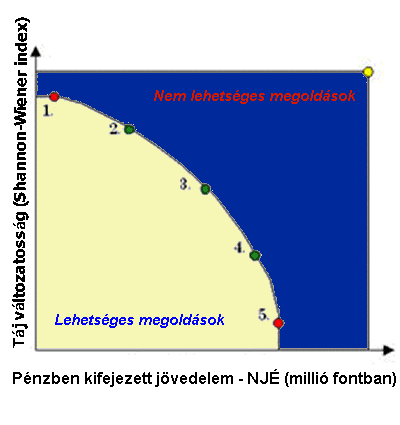
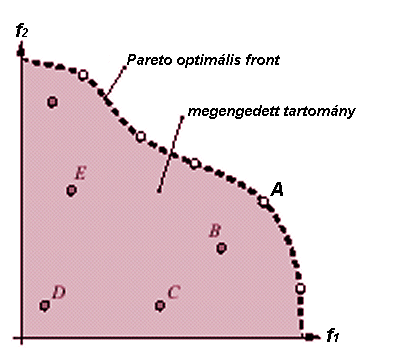
Az elmondottakat talán egyszerűbb megérteni egy ábra segítségével. A 6.43 ábrán felrajzoltuk két cél szerinti optimalizálás (például gazdaságosság és szociális hatékonyság) Pareto optimális frontját. A lilára festett terület jelképezi az összes lehetséges megoldás eredményét. A nagybetűvel jelölt körök egy-egy konkrét megengedett megoldási eredményt mutatnak. Egy cél szerinti optimalizáláskor (feltételezve, hogy az optimum a célfüggvény maximumát jelöli) az a megoldás jobb amelyik eredménye nagyobb. Ha azonban több célunk van (pld. mint az ábrán 2) akkor a "nagyobb" szó már nem alkalmazható a két megoldás eredményének az összehasonlítására. Ebben az esetben a megoldások egymáshoz képesti viszonyát a dominancia fogalmával fejezhetjük ki. Nem véletlenül különböztetjük meg a megoldást és a megoldás eredményét, mivel a megoldás az a vektor, mely behelyettesítve a célfüggvényekbe szolgáltatja a megoldás eredményét. Mivel a példán látható esetben két célfüggvény van egy megoldás vektor mind a két célfüggvényből generál valamilyen eredményt.

6.43 ábra - Pareto optimális front kétdimenziós esetben

Valamely a vektor akkor domináns a b vektor vonatkozásában, ha az a vektor eredménye nagyobb a b vektor eredményénél valamennyi cél vonatkozásában. Az ábra példáján az A ponthoz tartozó megoldás vektor domináns a B ponthoz tartozó megoldás vektorhoz képest, a B ponthoz tartozó megoldás vektor domináns a C ponthoz tartozó megoldás vektorhoz képest. Ha két pont esetében az egyik cél szerinti eredmény kisebb a másik pedig nagyobb (vagy fordítva) akkor a két ponthoz tartozó megoldás vektor indifferens egymáshoz képest.

Ezek után úgy is megfogalmazhatjuk a Pareto optimális frontot, hogy azt nem dominált megoldások eredményei alkotják, azaz olyan megoldások eredményei, melyekhez képest nem található domináns megoldási eredmény a lehetséges megoldások tartományában.

Az első kérdés, ami a Pareto optimummal kapcsolatban felmerülhet, hogy mi is lesz a végleges megoldás. A fogalom mint látjuk alternatív megoldásokat igényel és a végleges megoldást a szakemberekre vagy politikusokra bízza.

A másik kérdés, hogy miként lehet megtalálni a Pareto optimális fronthoz tartozó megoldás vektorokat a genetikus algoritmus segítségével. Erre a kérdésre kimerítő összefoglalást találunk Eckart Zitzler doktori disszertációjában [10] .

Mielőtt azonban erre rátérnénk egy ábra segítségével kibővítjük a genetikus algoritmussal kapcsolatban megismert tereket (6.44 ábra). Az első térben a kódolt egyedek a kromoszómák helyezkednek el. Ezt a teret hívjuk az egyedek terének . A genetikus algoritmus ebben a térben működik (ezek közül az egyedek közül kerül kiválasztásra a keresztezési populáció, ezek hajtják végre a keresztezést, mutációt, stb.).

Az egyedek teréből egy leképezéssel jutunk el a döntési térbe. A leképezés vagy dekódolás kiinduló példánk esetében megfelelteti az a betű kódját valamely földhasználatnak (pld. lombos erdő), helyét (a gén kromoszómán belüli sorszámát) pedig egy előre meghatározott táblának. Megjegyezzük, hogy másféle kódolás is elképzelhető ugyanerre a feladatra, amelyek közül egyet a LADSS-ban is kipróbáltak: a gének kódjai földhasználati százalékokat jelentenek, sorszámuk, pedig a kérdéses földhasználati százalék prioritásának felel meg. Kézenfekvő, hogy ebben az esetben a leképezés egy olyan allokációs függvény segítségével realizálódik, mely a kérdéses prioritásoknak megfelelően rendeli hozzá a földterületeket a kérdéses földhasználathoz. A döntési vektor esetünkben tehát nem más mind az egyedből ilyen vagy olyan leképezéssel létrehozható táblák szerinti földhasználat kijelölés.

A cél tér úgy jön létre, hogy a döntési vektorokat behelyettesítjük a hatáselemző modulokba - vagy egyszerűbben célfüggvényekbe (egy vektort mindig annyi célfüggvénybe helyettesítünk be, ahány cél szerint optimalizálunk).

6.44 ábra - a genetikus algoritmusban szereplő terek kapcsolata

A többcélú optimalizálás során a rangsor szerinti jóságot előzetesen a dominanciából vezetik le, majd egy megadott "fülke" sugár (s_share) nevű paraméter felhasználásával a közelítő jóságokat csökkentve véglegesítik.

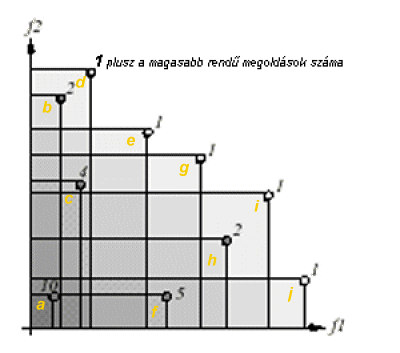
Az első lépésben tehát előzetes jósági értéket rendelnek az x_i kromoszómához mely értéke

jóság(x_i, t) = 1 + p_i^t,          (6.10)

ahol p_i^t azon kromoszómák száma, melyek az x_i kromoszómát dominálják a t populációban. A nem dominált kromoszómák előzetes jósági értéke tehát 1, minél rosszabb a kromoszóma, annál nagyobb az előzetes jósági értéke.

6.45 ábra - a előzetes jósági értékek többcélú optimalizáláskor két célfüggvény esetén

Ezután sorba állítjuk valamennyi kromoszómát oly módon, hogy az első helyen szerepeljenek a legjobb (tehát 1 előzetes jósági értékű) a végén pedig a legrosszabb (n* ≤ N) előzetes jósági értékű kromoszómák.

Elvégezzük a

Jóság(Ssz) = 2 - SP + 2·(SP - 1)·(N - Ssz) / (N - 1).

kifejezés szerinti másodlagos jósági érték interpolálást, majd az azonos előzetes jósági értékű kromoszómák másodlagos jósági értékeit átlagoljuk (gondoljunk arra, hogy több olyan kromoszóma is van amelyek előzetes jósági értéke azonos, pld. 1 mégis a sorba állítás után a képletből különböző másodlagos jósági értéket kapnak, ami nem indokolt, ezért kell másodlagos jósági értékeiket átlagolni, nem változtatva meg ezzel az őszjósági érték mennyiséget).

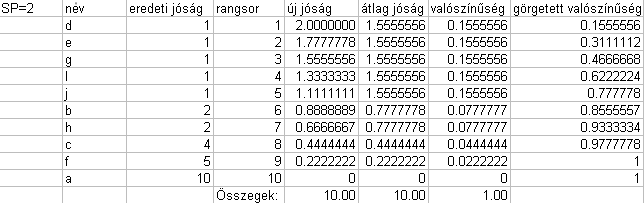
Hogy az elmondottak világosabbak legyenek a 6.45 ábra egyszerű példájára elvégeztük a hivatkozott számításokat, melyeket a 6.5 táblázatban és a belőle készült torta-diagramot tartalmazó 6.46 ábrán mutatunk be.

6.5 táblázat - rangsor szerinti jósági értékek számítása többcélú optimalizáláskor

6.46 ábra - a 6.5 táblázat szelekciós valószínűség értékeinek tortadiagramos ábrázolása

Figyeljük meg, hogy mind a 6.45, mind a 6.46 ábrán feltüntettük kis latin betűkkel jelölve az egyes kromoszómák nevét, az elnevezés természetesen független az aktuális rangsorolástól.

A végső jósági értékek kialakításához még szükség van az azonos rangú egyedek jósági értékeinek csökkentésére bizonyos távolsági paraméter alapján. Arról van tehát szó, hogy ha egymáshoz túl közel helyezkednek el azonos rangú egyedek, úgy jósági értéküket egyedileg csökkentik, de e mellett gondoskodnak arról, hogy a ranghoz tartozó összjósági érték ne változzon. A távolság meghatározható az egyed térben, döntési térben vagy a cél térben. Mivel a módszer azt kívánja elérni, hogy a Pareto front egyenletesen, de ne túl sűrűn legyen meghatározva, ezért célszerű a távolság fogalmat a cél térben értelmezni. A s_share küszöb távolság meghatározása bonyolult feladat, a LADSS Fonseca és Fleming javaslatát [11] alkalmazza, mely a célfüggvények maximális és minimális értékeiből illetve a Pareto frontot alkotó optimális pontok számából vezeti le s_share értékét.

Ha a küszöbérték megvan, akkor az i∈P egyed végleges F(i) jósági értékét a F'(i) előzetes jósági értékből a következő kifejezésből nyerjük:

F(i) = F'(i) / ∑_j∈P s(d(i,j))          (6.11)

A fülke szám azaz a kifejezés nevezője tehát nem más, mint a kérdéses egyed illetve a populáció egyéb egyedei között fellépő s csökkentő függvények összege.

Gyakran használt csökkentő függvény:

s(d(i,j)) = 1 - ( d(i,j) / s_share)^a, ha d(i,j) < s_share, egyébként s(d(i,j)) = 0.          (6.12)

A kitevőben szereplő a értéke rendszerint 1, a távolságok pedig a célfüggvény értékek négyzet összegéből vont négyzetgyökkel számíthatók, bár természetesen más normák is használhatók.

Ne felejtsük el, hogy a [11]-ben lévő eredeti javaslat szerint a fülkeszámmal csökkentett egyedi jóságok rangonkénti összege meg kell, hogy egyezzen a kérdéses rang szerinti jóság csökkentés előtti összegével, azaz, ha az r rangú csökkentés előtti jóság összeget S'(r)-el, a csökkentés utáni összeget pedig S(r)-el jelöljük, úgy az r rangú i egyed végleges F_r^veg(i) jóságát a következő képletből nyerjük:

F_r^veg(i) = F_r(i)·(S'(r) / S(r)).          (6.14)

A bemutatott szelekciós módszer csak egy az utóbbi évtizedben kidolgozott módszerek közül. A már hivatkozott [10] disszertációban számtalan más módszer között megismerhetjük a disszertáció szerzőjének módszerét is, mely nem használ "fülkéket", hanem két külön kromoszóma halmazt, egyet a domináns egyet pedig a dominált kromoszómák számára. A Pareto front egyenletes megjelenítését ez a módszer úgy éri el, hogy a "külső" - domináns egyed halmazban klasztereket alakít ki, melyeket a végső megoldásban centroidjaikkal reprezentál.

A műveletek definiálására illetve korlátozására is számtalan lehetőség van, például a LADSS 6.46 ábrán bemutatott kísérleti eredményeit létrehozó keresztezési műveletnél korlátozták a szülők egymástól mért távolságát.

További megválasztandó kérdés a leképező függvény illetve a kromoszómák kódolása, ami a LADSS példája esetében, ahogy azt már említettük két verzióban is kipróbálásra került. Az egyszerűbb és a próba futások során eredményesebb kódolási módszert a 6.47 ábra segítségével szemléltetjük.

6.47 ábra - a táblák szerinti kromoszóma kódolás szemléltetése (a gén sorrendje azonosítja a táblát, színe pedig a földhasználatot)

A leírt rendszer kipróbálására egy 90 táblából álló 9 lehetséges földhasználatot alkalmazó skót felföldi mezőgazdasági kutató állomás új földhasználat tervezésével kapcsolatban került sor. A két konfrontáló cél a táj változatossága, melyet a Shannon-Wiener indexszel számszerűsítettek illetve a gazdasági eredményesség (nettó jelenlegi érték = NJÉ), melyet angol fontban fejeznek ki. A 6.48 ábrán látható, hogy az egymás utáni populációk hogyan közelítik a Pareto frontot.

6.48 ábra - a táblák szerinti kromoszóma kódolással végrehajtott többcélú optimalizálás populációi

A 6.49 ábra érdekes összehasonlításra ad lehetőséget az egyéni szakértők, szakértő csoportok hagyományos módon végrehajtott földhasználat tervezése és a prioritással kiegészített földhasználat százalékos kódolással illetve tábla kódolással végrehajtott genetikus többcélú programozás között. Az ábráról egyértelműen leolvasható, hogy az egyéni illetve csoportos "gyalog" módszerek meg sem közelítik a Pareto frontot. Az is látható hogy a vizsgált feladat esetében a tábla szerinti kódolás nyújtja a legjobb eredményt. Az ábra feltünteti a jelenlegi földhasználatot is.

6.49 ábra - a földhasználat tervezési módszerek összehasonlítása

A 6.50-es ábrán a végeredményt látjuk generalizált formában.

6.50 ábra - a táblák szerinti kromoszóma kódolással végrehajtott többcélú optimalizálás generalizált Pareto frontja

Ha az 1 pontot választjuk, úgy maximális változatosság lesz minimális bevétel mellett, ha az 5 pontot akkor olyan monokultúrát termesztünk valamennyi táblán, mely maximális pénz hozamot eredményez, a 2, 3 és 4 pontok különböző kompromisszumokat reprezentálnak a két cél között.

A döntéstámogató rendszerek keretei

Már az eddigi tárgyalásunk során is igyekeztünk rámutatni a példáként szereplő rendszerek szoftver architektúrális jellemzőire, különös tekintettel a GIS és az egyéb modulok kapcsolatára. Jelen összefoglalásunkban elsősorban a különböző tematikus modellek kapcsolatát vizsgáljuk, s e mellett még bizonyos felhasználói szempontokat is szeretnénk a főbb keret-típusokhoz hozzákapcsolni.

Abból kell kiindulnunk, hogy a térbeli döntés támogató rendszerek alapvetően a mezőgazdasági, környezeti, regionális, közlekedési, katasztrófa-védelmi tervezéshez nyújtanak segítséget. A felsorolt és más területfüggő témákban a tervezés azt hivatott meghatározni, hogy az elhatározott műszaki, mezőgazdasági, szociális, stb. intézkedések milyen hatást gyakorolnak az élővilágra, a szociális szférára, környezetre, melyek a gazdasági hatások, stb. Ezeknek az intézkedéseknek valamely kompromisszum szerinti optimumot kell biztosítaniuk a várható hatások vonatkozásában.

A döntéstámogató rendszerek a hatások vizsgálatára specializált modelleket használnak, melyeket a korábbi egy-két évtizedben szűken specializált természet-, vagy társadalom tudósok fejlesztettek ki. Ezek a modellek egy-egy partikuláris jelenség outputját dolgozzák ki megadott input hatására. Ezek közül a modellek közül azokat, melyeket a tapasztalat igazolt és a kérdéses tudomány terület elfogadott az amerikai terminológiában "legacy" (örökség) modelleknek nevezik. Céljuk amint látjuk, elsősorban a jelenségek megismerése - a kutatás volt. További jellemzőik, hogy a kérdéses szakterület terminológiája alapján végzik az adat-meghatározást, különböző időben készültek, különböző információ technológiai szinten és eszközökkel. Ez utóbbi magyarul azt jelenti, hogy különböző program nyelveken íródtak, különböző operációs rendszerek alá.

Nagyon fontos jellemzőjük ugyanakkor, hogy a kódjuk kipróbált és használatukhoz a szakterületek ragaszkodnak.

A tervező vagy döntéshozó azonban nem kutatni akar egyes részterületeket, hanem olyan terveket akar megvalósítani, melyek számtalan szakterületi modell működését befolyásolják. A tervező feltételezi, hogy a modell a valóságot tükrözi és outputját alkalmazni akarja.

További jogos igénye a tervezőnek, hogy a döntési folyamatban a modellek esetleges kölcsönhatása is figyelembe vehető legyen.

A folyamatos fejlődésben lévő szoftver rendszereket elég nehéz osztályozni. Feltételesen elfogadhatjuk Westervelt és Shapiro [12] osztályozását, mely szerint megkülönböztetünk

• önálló programokat;
• közös adatokra és eljárásokra támaszkodó rendszereket;
• folyamatok közti kapcsolatot realizáló architektúrákat;
• dinamikus modell kapcsolattal rendelkező rendszereket;
• szétosztott objektumokkal működő szoftvereket;
• új modellező nyelveken alapuló fejlesztéseket;
• oktatási modellező rendszereket.

• Az önálló programokból álló rendszerekre több példát is bemutattunk. Amint láttuk a modellek különböző nyelveken készültek, térbeli - GIS integráltságuk különböző fokú és jellegű volt, igen hasznosaknak bizonyulhatnak egy szűk felhasználói közösség számára.

Általános igény ugyanakkor ezekkel a programokkal szemben, a könnyebb, szélesebb rétegek által való használat, ami maga után vonja a szoftverek gazdaságosságának növekedését, valamint az, hogy az ilyen modellek használjanak más szakterületi modellekkel kapcsolható interdiszciplináris fogalmakat és adatokat.

• A közös adatokra és eljárásokra támaszkodó rendszerekre jó példa néhány nyitott, programozható GIS szoftver által megvalósított modell integráció. Különösen az ingyenes GRASS GIS alkalmas erre a célra, mely szubrutin könyvtáraihoz kapcsolhatók a természeti és társadalmi modellek. Más példák az ESRI ArcView GIS Avenue nevű programnyelvét használják a modellek integrálására. Ebben az architektúrában több modell fut ugyanazon a számítógépen, ugyanazon operációs rendszer alatt, virtuálisan a GIS szoftver részeként azaz közösen használva a GIS adatokat és műveleteket. Rendszerint a GIS szoftver grafikus felhasználói interfésze bővítésével érhetők el a modellek, de lehetőség van önálló grafikus felhasználói interfész kialakítására is mint ahogy az IPDSS esetében láttuk. Akármelyik megoldást is alkalmazzák, a közös interfész egyszerűsíti a tanulási folyamatot és szélesebb felhasználói körök számára teszi hozzáférhetővé a rendszert. Az ilyen rendszerek létrehozása akkor nehezül meg, ha a modellező modulok már rendelkeztek beépített grafikus - megjelenítő rendszerrel. Szerencsére a legtöbb régi modellező szoftver még a grafikus interfészek megjelenése előtt készült, ezért a kódjaikat nem kell átírni, hanem csak a bemenő és kimenő adatokat kell a közös adatformátumba transzformálni.
• A folyamatok közti kapcsolatot realizáló architektúrák annyiban különböznek az előző csoporttól, hogy az egyes modellező programok változatlanul kerülnek alkalmazásra a létrehozandó rendszerben. Minden modellező program megtartja a saját felhasználói interfészét, a keret program feladata, hogy meghatározza az egyes modulok egymásutánját, illetve hogy a megelőző modul outputját átalakítsa a követő modul inputjába.

Ilyen rendszert legegyszerűbben mint operációs rendszerbeli (DOS vagy UNIX) szkriptet lehet elkészíteni. Az operációs rendszerek fejlődésével azonban megjelent a folyamat grafikus programozásának igénye. Ilyen grafikusan programozható keretrendszer a FRAMES (Framework for Risk Analysis in Multimedia Environmental Systems = Kockázat Elemző Többközegű Környezeti Keretrendszer), melyet a Pacific Northwest National Laboratory nevű amerikai állami kutatóintézet készített el és bocsát ingyen a felhasználók rendelkezésére. A rendszer egységes output formátumot alkalmaz, mely változatlan formában inputként jelentkezik más programok számára (6.51 ábra).

6.51 ábra - a FRAMES felépítése

Ez a körülmény ugyan igényli a modellező modulok be-, és kimeneti kódjának átírását, a tényleges modellező részeket azonban nem érinti. A figyelembe vett közegeket, melyben a szennyezés terjed illetve a rájuk vonatkozó modellező modulok egymásutánját a felhasználó a grafikus interfészen ikonok kiválasztásával és összekötésével jelölheti ki (6.52 ábra).

6.52 ábra - a FRAMES grafikus felhasználói interfésze

Az eredmények megjelenítését a FRAMES grafikus csomagja teszi lehetővé.

A csoport nagy előnye, hogy a hagyományos modellező programok lényegi változás nélkül használhatók, fejlesztésükben nem kell figyelembe venni az integrációs igényeket, ugyanakkor a gyakorlati feladatok komplexen, több tényező figyelembe vételével viszonylag egyszerűen állíthatók össze. Természetesen az ilyen típusú rendszerek eredményes használatának is döntő feltétele megfelelő tematikus térbeli adatbázisok megléte.

• A folyamatok közti dinamikus kapcsolatot realizáló architektúrák azt igénylik, hogy a modulok futás közben is képesek legyenek az adatcserére - a visszacsatolásra. Ilyen feladatokra az előző architektúra szekvenciális alapkoncepciójából kiindulva nem alkalmas. Ezt az igényt úgy lehet kielégíteni, ha az egész modellből egy programot csinálunk olymódon, hogy az egyes modulok ebben a programban szubrutinokként vagy objektum orientált program esetén objektumokként legyenek jelen. Az architektúra működését, előnyeit már viszonylag részletesen tárgyaltuk a DIAS példáján.
• Hálózaton szétosztott objektumokról már sok szó esett az előző fejezetekben. Az az új koncepció, hogy egy nagy szuper komputer helyett számtalan hálózattal összekapcsolt komputeren oldjuk meg a nagy processzor igényű feladatokat a hálózatok technikai tökéletesedésével kezd ábrándból reális elképzeléssé válni. Ahogy azonban a WEB GIS-szel kapcsolatban már elmondtuk a technológia még nem érett, várhatóan 2-3 év szükséges a megszokott alkalmazásához.

Ugyan ezt mondhatjuk el a hálózatos, dinamikus kapcsolatot realizáló komplex modellezésről is azzal a különbséggel, hogy itt a hálózatos módszerek komersszé válásához még több időre (5-6 év) lesz szükség. Példaként az érdeklődő tanulmányozhatja a Virginiai Egyetem Legion projektjét a világméretű virtuális komputerre és a gyakorlati kipróbáláshoz le is töltheti a projekt keretében készült kliens szoftver 1.7 verzióját.

• Az új modellező nyelvek azt az integrációs feladatot célozzák meg, hogy lehetővé tegyék a szaktudományokon belül kifejlesztetett modellező algoritmusok automatikus integrálását egy koordinált részekből álló szoftver programba.

Talán legjobb példája ennek a típusnak az SME (Spatial Modeling Environment = Térbeli Modellező Környezet). A UNIX-os szoftver szabadon letölthető az SME honlapjáról. A rendszer kombinálja a Stella típusú szimuláció modellező szoftvert a szimulációt hatékonyan végrehajtó környezettel. Az SME párhuzamosan futtatja a Stella-szerű szimulációs modelleket, melyek a raszter GIS adatbázis celláihoz vannak kapcsolva. Az inicializáló paramétereket a modellek a GIS fedvényekből nyerik. Az SME lefordítja a cella szimulációt specifikáló modelleket a közös MML (Modular Modeling Language) nyelvre és későbbi használatra könyvtárakat hoz belőlük létre. Térbelileg explicit szimulációs modelleket a korábban könyvtározott modulok kiválasztásával, a változók illesztésével és az aktualizált modell C++ nyelvre fordításával lehet az SME kódgenerátora segítségével létrehozni.

• Az oktatási modellező szoftvereket az új modellező nyelvek olyan részhalmazának tekinthetjük, melyek főfeladata, nem a nagyon összetett modellek létrehozása, hanem az, hogy a programozásban nem túl képzett hallgatók gyorsan létre tudjanak hozni multidiszciplináris modelleket. Példaként megemlíthetjük a már többször emlegetett Stellát, a Powersim Studio 2000 Express-t (ez az oktatási verzió 90 napos használatra szabadon letölthető), de leginkább a MIT Media Lab-ban készített Javában írt tehát platform független StarLogo-ra szeretném felhívni az érdeklődők figyelmét, mely a honlapról szabadon letölthető.

Végül foglaljuk össze egy táblázatban az egyes típusok főbb tulajdonságait a használat és fejlesztés legfontosabb szempontjai alapján:

	"hagyományos" szoftver használat	tudósok kellenek a működtetéshez	szétosztott feldolgozás	rendszerek közötti visszacsatolás	gyors modell fejlesztés	multidiszciplináris modellezés	elérhető a nem szakemberek számára
önálló programok	5	5	3	0	0	0	0
közös adatok és eljárások	4	5	3	1	2	1	0
folyamatok közötti kapcsolatok	3	4	4	2	1	2	0
folyamatok közötti dinamikus kapcsolatok	2	4	4	5	1	4	1
kapcsolatok szétosztott objektumokkal	1	3	5	5	1	5	2
új modellező nyelvek	0	1	5	5	5	5	5
oktatási modellezés	0	0	0	0	5	5	5

6.6 táblázat - a modellező szoftver megközelítések összehasonlítása

Az egyes típusok jóságát 0-tól 5-ig terjedő osztályzatokkal és hozzájuk választott színekkel értékeltük. Nem nehéz rájönni, hogy a megfelelő kerettípus megválasztása tulajdonképpen a már jól ismert többcélú (de nem térbeli) optimalizálási feladat. Természetesen még több célt is felsorolhattunk volna, de a bemutatottak alapján is belátható, hogy a választás mindenképpen kompromisszummal jár. A fő probléma tulajdonképpen a "hagyományos" (legacy) modellek változatlan felhasználásában van. Talán nem járok messze az igazságtól, ha úgy gondolom, hogy a szaktudományok fejlődésével ezek a modellek is előbb utóbb elavulnak és a jövőbe mutató döntés az új modellező nyelvek alkalmazásán alapulhat. Ez az állítás akkor is igaz, ha bizonyos régi modell algoritmusa maradandónak bizonyul. Ebben az esetben azt felhasználhatjuk az új modell kifejlesztéséhez.

⁽¹⁾ A tanulmány része az OTKA T 031719 témaszámon folyó kutatásnak.

· a következő részben az intelligens gépjármű navigációs rendszereket tárgyaljuk

· esetleg visszatérhet az előző részhez

· illetve a tartalomjegyzékhez

---

Megjegyzéseit E-mail-en várja a szerző: Dr. Sárközy Ferenc

---