Műholdas helymeghatározás I

Ebben a részben megismerkedünk

a műholdas helymeghatározás geometriai alapelvével,
a GPS és GLONASS rendszer felépítésével,
a kódfázis és
vivőfázis mérés fogalmával, valamint
a GPS és GLONASS hibaforrásaival.

Amint az az alpont címéből is következik több műholdas helymeghatározó rendszer is létezik illetve létezett, s a jövő tervek hasonlóképpen gazdagok új műholdas megoldásokban.

A jelenlegi szabatos műholdas helymeghatározó rendszerek közvetlen előzménye az USA Haditengerészete számára 1961-ben kifejlesztett TRANSIT műholdas navigációs rendszer, mely polgári felhasználása 1967-ben kezdődött, s 1994-ben a rendszer működésével együtt véget is ért.

A rendszer alapvető célja tengerészeti navigáció volt, de hasznosították geodéziai célokra is, elsősorban olyan globális feladatok megoldására, mint a NAD 83 nevű északamerikai, vagy a WGS 84 nevű globális dátum létrehozása. A TRANSIT rendszer geodéziai hasznosítását hosszú észlelési idő, utófeldolgozás és viszonylag alacsony, 1 m. körüli pontosságok jellemezték. A TRANSIT rendszerben a mérés alapelve az volt, hogy a vevő a földi pont és a műhold távolságának megváltozását határozta meg egy megadott időintervallumra a Doppler csúszások segítségével (lsd. [5]), ezért ezekre a műholdakra a geodéták rendszerint 'doppleres' jelzővel hivatkoztak. A TRANSIT-tal egyidejűleg a Szovjetunióban is kifejlesztettek egy műholdas navigációs rendszert, ezt azonban kizárólag katonai célokra használták és titokvédelmi okokból jellemzőit nem publikálták.

Mind a jelenleg működő, mind pedig a tervezettek között találunk olyan kispontosságú rendszereket, melyek helyzeti pontossága néhány száz métertől egy-két kilométerig terjed. Ezek a rendszerek a korábbi repülőgépes illetve hajós impulzusos rádionavigációs rendszerek (SHORAN, HIRAN stb.) műholdas továbbfejlesztései. Ilyen rendszer pld. az ARGOS, mely két TIROS N meteorológiai műholdat használ az állatok helyváltoztatásának tanulmányozására. Az állatokra kb. 2 kg. súlyú rádióadót erősítenek, mely 401.650 MHz frekvencián sugároz. a műholdak veszik a jelet és továbbsugározzák a földi feldolgozó állomásra. A feldolgozó állomás a keresett koordinátákat egy hold vételéből vezeti le mozgó tárgyak esetében ±800 m., rögzített tárgyak esetében pedig ±300 m. középhibával.

A számtalan új kezdeményezés közül csak megemlítjük az intelligens autónavigációs rendszerekben fölhasználásra tervezett LORAN C repülőgép navigációs rendszert, mely mérőelemei két alacsony pályamagasságú úgy nevezett LEO szatellitán illetve a mozgó gépkocsin helyezkednek el, az eredmények (a gépkocsik koordinátái) pedig a műhold kommunikációs csatornáján keresztül jutnak a földi állomásra. A rendszer egy variánsát a GEOSTAR távközlési szatellita segítségével próbálták ki 1993-ban.

A fenti áttekintés azt kívánta bemutatni, hogy már jelenleg is többféle műholdas rendszer használható különböző pontossági és szolgáltatási paraméterrel, és ez a jövőben a műholdas távközlés fejlődésével még inkább így lesz. Egyre több ugyanis az olyan feladat, amelyben a mérés eredményét nem a mért objektumon, hanem attól távol kívánjuk jelen időben megkapni. Ha a pontossági igények nem túl nagyok, az ellenőrzött objektumok száma pedig igen nagy, úgy olcsóbb lehet az ilyen feladatokat olyan saját szatellita rendszerrel megoldani, mely egyben az adatátvitelt is elvégzi.

A műholdas helymeghatározás geometriai alapelve

A korszerű műholdas helymeghatározó rendszerek a pontok helyzetét térbeli ívmetszéssel határozzák meg.

3.89 ábra - egy távolság mértani helye a gömb

3.90 ábra - két gömb metszésvonala kör

3.91 ábra három gömb két pontban metszi egymást

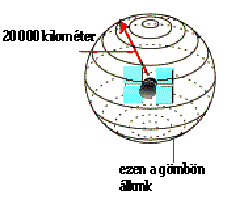
Képzeljük el, hogy egy rögzített pillanatban megmértük álláspontunk és egy műhold távolságát. Legyen ez a távolság 20 000 km. Egy mérés alapján álláspontunkról csak azt tudhatjuk, hogy valahol azon a gömbön van amelyet a kérdéses műholdra mint középpontra 20 000 km.-es sugárral szerkesztünk (3.89 ábra).

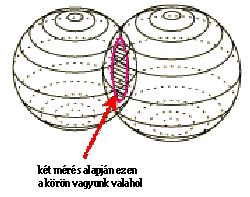
Ugyanebben az időpillanatban mérjük meg a távolságunkat egy másik műholdtól is. Legyen ez a távolság 21 800 km. Kézenfekvő, hogy álláspontunk rajta van azon a gömbön is, melyet a második műhold mint középpont körül 21 800 km.-es sugárral szerkeszthetünk. Mivel az álláspontunk mindkét gömbön rajta van rajta kell, hogy legyen a két gömb metszésvonalaként létrejött körön (3.90 ábra).

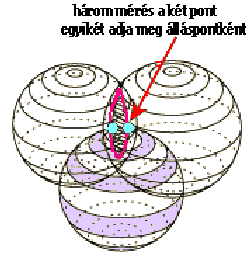
Ha ugyanebben a pillanatban egy harmadik műholdtól is megmérjük a távolságot, legyen ez 23 600 km. és elképzeljük a harmadik gömböt is, úgy ez utóbbi két pontban metszi az első és második gömb metszésvonalát. A két pont közül a valódi álláspont további mérés nélkül néhány egyszerű szabály figyelembe vételével meghatározható (3.91 ábra).

Nem szabad elfelejtenünk, hogy a fenti gondolat-kísérletnél a három mérést egy időpillanatban hajtottuk végre és ismertnek tételeztük fel ebben az időpillanatban mind a három műhold koordinátáit.

A GPS és GLONASS rendszer felépítése

A továbbiakban azonban a világszerte elterjedt GPS rendszerrel fogunk foglalkozni, Mielőtt azonban ezt megtennénk szólnunk kell arról, hogy a GPS-hez hasonló rendszer üzembeállítását a Szovjetunióban is megkezdték, azonban a Szovjetunió tönkretétele után a kiépítés üteme lelassult. A későbbiekben ismertetendő 'szelektív hozzáférés' fedőnevet viselő amerikai politika miatt azonban az amerikai civilek is szeretnének egy olyan kiegészítő mérőrendszerre támaszkodni, mely adatait nem hamisítják mesterségesen. Ezzel magyarázható, hogy az amerikaiak által GLONASS-nak nevezett szovjet (orosz) műholdas szabatos navigációs rendszer teljessé tételére az amerikai üzleti körök pénzügyi támogatást ajánlottak fel az orosz kormánynak, és amerikai cégek olyan vevők készítését kezdték meg, melyek a méréshez mind a GPS mind a GLONASS műholdak jeleit felhasználják. 1993-ban 13 műhold üzemelt a tervezett 21 működő és 3 tartalék, összesen 24 műholdból, melyek három pályasíkban keringenek 19.1 km.-es közepes magasságban. Hozzá kell még fűznünk, hogy a két rendszer összekapcsolása azért is előnyös, mivel a két rendszer műholdjai olyan pályákon keringenek, melyek kiegészítik egymást, és biztosítják, hogy a föld minden pontján minden időben kellő számú, optimális helyzetű műholdat lehessen észlelni.

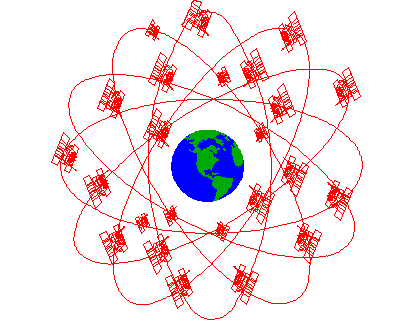
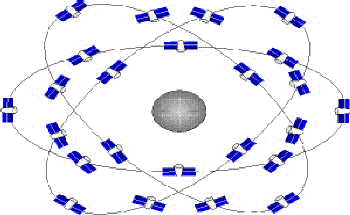
A GPS fejlesztésének megkezdését 1972-ben kezdeményezte az Egyesült Államok Védelmi Minisztériuma (US. Department of Defense, röviden DoD). Olyan rendszert szándékoztak megvalósítani mely a szatelliták ismert pozícióiból távolságokat határoz meg ismeretlen helyzetű földi, légi, tengeri objektumokra. Elsődlegesen a rendszer létrehozása katonai célokból történt, de a polgári hasznosítással is számoltak.

A rendszer ürszegmense 21 aktív és 3 tartalék műholdból áll, melyek hat darab 55^o inklinációjú sikban helyezkednek el. Mind a 6 sikban négy műhold kering 20 200 km. magasan közel kör alakú pályán.

3.92 ábra - a GPS műhold

A pályákat úgy képzelhetjük el, hogy az egyenlítőt hosszúság szerint 30^o-ként felosztjuk, majd minden egymástól 180 fokra fekvő két osztásponton keresztül fektetünk egy olyan körlapot, mely középpontja egybeesik a föld középpontjával, sugara 26 370 km., s az egyenlítő síkjával bezárt hajlásszöge 55^o. A műholdak súlya mintegy 750 kg. Ma, a rendszer teljes kiépülése után a föld bármely pontjáról egyszerre 4-8 műhold 'látható' 15^o-ot meghaladó magassági szög alatt. A 3.93 és 3.94 ábrán felvázoltuk a GPS és a GLONASS rendszerek pályáit és a műholdak elhelyezkedését a pályákon.


3.93 ábra - a GPS pálya síkok és a műholdak helyzete a pályákon	3.94 ábra - a GLONASS pálya síkok és a műholdak helyzete a pályákon

Az első GLONASS műholdat 1982 októberében lőtték fel. 1995 végéig több mint 70 műhold került a pályára. A műholdak súlya mintegy 1500 kg., tervezett működési ideje 3 év. A tervek szerint az 1998-tól kezdődően felbocsátandó műholdak tervezett működési ideje 5 év lesz.

A teljes kiépítésben a 24 darab GLONASS műhold 19 100 km.-es közel kör alakú pályán kering három pálya síkban, melyek felszálló ága egymástól 120^o-ra helyezkedik el. A pályánként 8 műhold egyenlő távolságra van egymástól, szélesség szerinti attribútum különbségük 45^o. A pálya inklinációja 64.8^o, egy teljes pálya megtétele kb. 11 óra 15 percig tart. A műholdak pályáját úgy tervezték meg, hogy egyszerre legalább 5 holdat lásson a felhasználó.

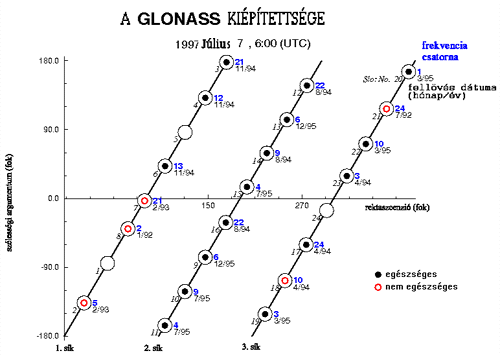
A 3.95 ábrán bemutatjuk a GLONASS rendszer 1997 július 7.-ei készültségi állapotát.

3.95 ábra - a GLONASS rendszer kiépítettsége 1997 07 07

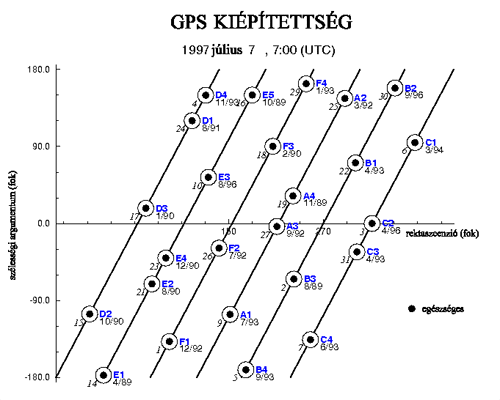
3.96 ábra - a GPS rendszer kiépítettsége 1997 07 07

A GPS rendszerről készült hasonló készenléti ábra (3.96 ábra) tanulsága szerint pillanatnyilag a GPS a teljes kiépítettség állapotában van.

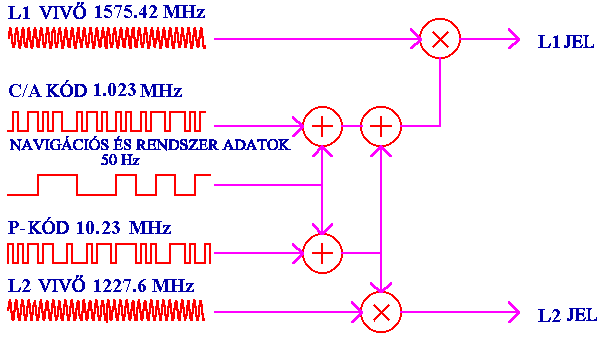
3.97 ábra - a GPS műholdak által sugárzott jelek

A GPS műholdak két jelet sugároznak. Az első jel vivőhullám hossza L1=1575.42 MHz., a másodiké L2=1227.60 MHz. E frekvenciákat a nagypontosságú atomórával stabilizált 10.23 MHz-es alapfrekvencia sokszorozásával állítják elő. Mindkét vivőhullámot modulálják a körülbelül 30 méter hullámhosszú P kóddal (P a precision - szabatos rövidítése). Az L1 vivőt ezen kívül modulálják még a C/A (coarse/acquisition - durva/elérés) kóddal, mely kb. 300 m. hosszú (3.97 ábra). A vevő ezeknek a kódoknak a felhasználásával határozza meg a pseudotávolságokat. A P kód nagyobb, a C/A kód kisebb pontosságot biztosít a pseudotávolságok meghatározásában.

Az eredeti katonai célokkal összhangban a DoD a szelektív elérhetőség (selective availability, röviden SA) politikáját gyakorolja, ami azt jelenti hogy esetenként (pld. az öbölháború idején) korlátozza a teljes rendszer használatát a polgári alkalmazóknak.

Gyakorlatilag ez korábban úgy történt, hogy csonkolták azokat az üzeneteket, melyek a műhold koordinátáit továbbítják a vevőknek. Jelenleg, időnként a C/A kódra műholdanként változó, alacsony frekvenciás (hosszú idő alatt ismétlődő) torzítást visznek, mely az eredeti 30 m-es pontosságot 100 m. körülire csökkenti.

A közeljövőben emellett tervezik az úgynevezett 'átejtés' kivédő (anti-spoofing) tehnika bevezetését, ami tulajdonképpen azt jelenti, hogy az új P kódhoz (Y kód) és a P kóddal modulált vivőhullámokhoz is csak a DoD által terjesztett hardver kulccsal lehet hozzáférni.

A tervek szerint 2000-ben állítólag meg fogják vizsgálni, hogy továbbra is szükség van-e az SA-ra.

A GPS a WGS-84 referencia rendszert használja. A műholdak pillanatnyi, időponttal jelölt koordinátái a navigációs üzenetben foglalnak helyet, melyet mind a P mind a C/A kód tartalmaz. Természetes, hogy az eredeti feldolgozás a GPS saját referencia rendszerében történik. Ha más referencia rendszerben dolgozunk, és Magyarországon ez az általános eset, úgy a mérési eredményeket transzformálni kell a használt referencia rendszerbe. Erre akkor van lehetőség, ha a méréssel érintett területen vagy annak közelében legalább 3 olyan alappontunk van, melyek koordinátái mindkét rendszerben ismertek. Sok országban, így nemsokára hazánkban is, a transzformációs paramétereket az országos geodéziai szolgálatok biztosítják a felhasználók számára.

A GLONASS rendszer műholdjai szintén két jelet sugároznak folyamatosan: az SP szabványos pontosságú jel a HP pedig nagy pontosságú. A polgári felhasználók számára csak az SP hozzáférés engedélyezett, ezt azonban nem rontják el mesterségesen. Az SP L1 vivőfrekvenciája a műholdak számára egyedi és az L1 = 1602 MHz + n * 0.5625 MHz képletből számolható, ahol n a műhold sorszáma. A 3.95 ábra tanulsága szerint egyszerre több azonos sorszámú műhold is működhet (pld. a 6-os vagy 24-es) ezek azonban úgy helyezkednek el, hogy egy álláspontból egyszerre ne legyenek láthatók. A GLONASS jel is tartalmaz navigációs és rendszer üzenetet.

A GLONASS rendszer a PZ-90 geocentrikus, földhöz kapcsolt referencia rendszerben működik és az a=6378136 m., f=1:298.257839303 paraméterű földi ellipszoidot használja. Jelenleg még nem ismert végleges transzformáció a PZ-90 és a WGS-84 között.

A kódfázismérés fogalma

A 3.97 ábrán láttuk, hogy a GPS az úgynevezett C/A kóddal csak az L1 vivőt modulálja, míg a P kód és a navigációs üzenet mindkét vivőre rákerül. Mivel a P kód titkosság alóli felszabadítására nincs remény, a kódfázismérés megismerésekor a C/A kód felhasználására fordítjuk a figyelmünk.

3.98 ábra - a C/A pseudo véletlen kód részlete

A C/A kód úgynevezett pseudo véletlen kód (bár meghatározott szabályok szerint készül mégis úgy néz ki mintha zaj lenne), zérusok és egyesek egymásutánja, egy elem frekvenciája 1.023 MHz, a kód 1023 bit hosszú, ami időben kifejezve 1 milliszekundumnak (0.001 mp.-nek) felel meg. Egy elem hossza tehát
2.99792458*10⁸*0.977517106*10^-6=293.052 m., az egész kódsorozat pedig hosszban kifejezve 293.052*1023=299792.458 m.

Míg a GLONASSrendszerben a vivő frekvenciát, addig a GPS rendszerben a C/A kódot rendelik a műholdakhoz, azaz minden műhold más és más szabály szerint készíti a pseudo véletlen kódot. A 3.99 ábra bemutatja a kód egy részének illusztrációját mind a 32 műholdra. A sorok fentről kezdődő sorszáma megfelel a műhold azonosítójának, a sötét bitek az egyeseket, a világosok a zérusokat reprezentálják.

3.99 ábra - 32 GPS műhold C/A kódjának részletei

A C/A kódot azonban nem csak a műholdak generálják, hanem a vevők is minden milliszekundum kezdetén. Ha az adó órája és a vevő órája pontosan ugyanúgy járna, akkor a vett jel és a vevő jele közti fáziseltolódás kizárólag a műholdról kibocsátott jel terjedési idejétől függne.

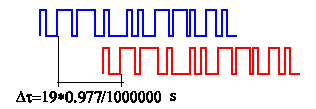
A 3.100. ábrán kék színnel ábrázoltuk a vevő által gyártott kódot, pirossal pedig a vett demodulált jelet. Mivel egy impulzus bit időben kifejezett értéke 0.977517106*10^-6 másodperc, az ábrán látható érték 19*0.977517106*10^-6 másodperc, ami 5567.993 m-nek felel meg.

3.100 ábra - a vett és a vevő által generált C/A kód időkülönbsége

A figyelmes olvasónak feltűnhet, hogy miként lehet egy egészében 299.792 km-es kóddal több mint 22 000 km-es távolságokat megmérni. Bár erre vonatkozó információt a GPS oktató irodalomban nem igen találunk, a megoldást rendszerint úgy kapják meg a szoftverek, hogy figyelembe veszik az álláspont közelítő koordinátáit (amit az előzőleg mért álláspont koordinátáival vesznek azonosnak) és kiszámolják, hogy az előző álláspont és a műholdak aktuális helyzete közötti távolságokban hányszor volt meg a 299792.458 méternyi teljes kódhossz. Az így kapott értékeket ezután érvényesnek tekintik az új álláspontra is.

A vevők tehát megmérik a szatelliták távolságát és kiolvassák a kódolt információból a műholdak helyzetére vonatkozó adatokat. Geometriai szempontból az álláspont ismeretlen koordinátái akkor számíthatók, ha ezek a mérések illetve helyzeti információk egyidejűleg három műholdra rendelkezésre állnak.

A mért távolságokat azért nevezik pseudo távolságoknak, mivel értéküket a vevő órájának a műhold órájához viszonyított késése is befolyásolja. A műholdakon nagypontosságú atomórák vannak, melyek szinkronizálásával a földi irányító központ foglalkozik. A vevőkbe ugyanakkor gazdaságtalan lenne ilyen drága atomórákat beépíteni, arról nem is beszélve, hogy központi szinkronizálásukat sem lehet technikailag megoldani. Az ismeretlen óra késést egy negyedik műholdra végzettt méréssel lehet meghatározni.

A pseudo távolságok meghatározása történhet a kódok felhasználásával. Az esetek többségében a vevők a C/A kódot értékelik ki a korrelációs technika segítségével. A korreláció alapelve azonos azzal amit az automatizált fotogrammetriai kiértékeléssel kapcsolatban már megismertünk, áramköri megvalósítása azonban olyan, hogy biztosítja a szatellita jel mindhárom komponensét: a műhold óra leolvasását, a navigációs üzenetet és a moduláció nélküli vivőhullámot. Míg a két utóbbi minősége független a megfejtett kódtól, addig az időleolvasás pontossága függ a kód periódusától (hosszától). A periódusnak a C/A kód esetén amint láttuk kb. 300 m. távolság felelt meg, míg a katonai használatú P kód esetén 30 m. A szatellita órajelét 1% pontossággal lehet detektálni ezért ideális esetben a C/A kód alkalmazásával végzett pseudo távolság mérések 3 m., a P kód segítségével végzettek pedig 0.3 m.-es pontossággal rendelkeznek.

A vivő fázismérés fogalma

A kódokat és jeleket a GPS az L1 és L2 ferkvenciák modulálásával juttatja el a vevőkhöz. Ezek a frekvenciák természetszerüleg sokkal magasabbak a kódok frekvenciájánál. Míg a pontosabb P kód hullámhossza 30 m., addig az L1 vivő 1575.42 MHz frekvenciája 19 cm.-nek felel meg.

A vivő fázis mérésre kialakított vevők áramkörei képesek a kódolás mentes vivő hullámhossz helyreállítására és meg tudják mérni a vivő fázisát is, azaz meg tudják határozni, hogy a vevő és műhold közötti teljes távolságban az utolsó nem teljes vivő hullám hanyad része az egész 19 cm.-es hullámnak. A probléma 'csak' az, hogy a mért hosszban százmillió körüli jelöletlen egész hullám is található, melyek megszámolása direkt módon technikailag lehetetlen.

Az egész hullámhosszak meghatározásához a vevők hardveresen annyiban tudnak hozzájárulni, hogy rögzíteni tudják az egyes műholdakra vonatkozó teljes hullámhosszak változását. Ha ugyanis a vevő mozdulatlanul áll az állásponton és méri négy műhold távolságát, a műholdak mozgása következtében a távolságok (a teljes hullámok száma és a nem teljes hullám részek nagyságai azaz a fázis mérési eredmények) változni fognak. Ezek a változások rögzíthetők és tárolhatók.

Ahhoz hogy a feladatot jobban el tudjuk képzelni írjuk fel az észlelések és a kordináták közötti összefüggést kissé egyszerűsített formában. Jelölje az i index a műholdakat, a j index az észlelési alkalmakat, fekete szín az ismert állandókat, piros szín az ismeretleneket, zöld szín a mérési eredményeket, lila szín a navigációs űzenetből nyerhető műhold koordinátákat.

Alkalmazzuk a következő jelöléseket:

x, y, z - az álláspont koordinátái;
X_i^j, Y_i^j, Z_i^j - az i-ik műhold koordinátái a j-ik észlelési pillanatban;
h - a vivő hullámhossza;
c - a hullám terjedési sebessége;
N_i - a teljes hullámhosszak száma az i-ik műholdhoz a kezdő pillanatban;
df_i^j - a nem teljes hullám rész hossz (a teljes hullámot egységnek tekintve) az i-ik műholdra végzett észlelés során a j-ik időpontban;
dN_i^j - a teljes hullámhosszak számának változása az i-ik műholdhoz a j-ik pillanatban a kezdő pillanathoz képest;
delta^j a vevő órájának eltérése a GPS időhöz képest a j-ik időpillanatban.

Egy észlelésre és egy műholdra tehát az alábbi összefüggés írható fel az álláspont és műhold távolságára:

[(x - X_i^j)² + (y - Y_i^j)² + (z - Z_i^j)²]^0.5

(N_i + dN_i^j + df_i^j).h + delta^j.c

Készítsünk egy táblázatot, melyben feltüntetjük az észlelési alkalmak számát a megfelő ismeretlen és egyenlet számot, feltételezve hogy egyidejűleg mindíg négy műhold távolságát mérjük. Nem nehéz észrevennünk, hogy három észlelés esetén, már nagyobb az egyenletek száma mint az ismeretleneké, tehát az ismeretlenek kiegyenlítéssel meghatározhatók.

észlelési alkalmak száma	1	2	3
ismeretlenek száma	3+4+1=8	3+4+2=9	3+4+3=10
egyenletek száma	4	8	12

A gyakorlatban a vivő fázismérésen alapuló módszerek rendszerint két GPS vevőt alkalmaznak. A cél ezeknél a módszereknél az úgy nevezett relatív helymeghatározás. A relatív helymeghatározás azt jelenti, hogy két pont közötti távolság X, Y, Z komponenseit kivánjuk meghatározni.

Az egyik vevőt az ismert referencia ponton üzemeltetik, míg a másik vevő a meghatározandó ponton üzemel. Mindkét vevő a megadott programnak megfelelően megméri a kijelölt műholdakra a vivő fázist és rögzíti a hozzátartozó idővel együtt. A feldolgozási folyamatban (utófeldolgozásról van szó) a program a vivőfázis észlelések különbségeiből számolja a keresett koordináta különbségeket.

Megkülönböztetik az egyszeres, kétszeres és háromszoros különbségeket (differenciákat).

Az egyszeres differenciák esetén az A referencia és B meghatározandó ponton azonos időben azonos műholdra végzett fázismérések eredményeit kivonják egymásból, ezért az i és j indexektől eltekinthetünk és ha a vevők és szatelliták távolságát T_A-val és T_B-vel jelöljük (azaz
T_A = [(x_A - X_i)² + (y_A - Y_i)² + (z_A - Z_i)²]^0.5, stb. észlelési egyenletként a következő kifejezést kapjuk:

T_B - T_A = (N_B - N_A + df_B - df_A).h + (delta_B - delta_A).c

Mivel a relatív helymeghatározásban a kiinduló pont koordinátáit ismertnek tételezik fel, egy fenti egyenlet három koordináta ismeretlent, szatellitánként egy (azaz n_i) egészhullámszám ismeretlent és mérési alkalmanként (n_t) egy óra eltérési ismeretlent tartalmaz. Azaz a megoldhatósághoz az
n_i.n_t mérési egyenletszámanak nagyobbnak kell lennie mint 3 + n_i + n_t.

Ha például 5 műholdra végzünk két alkalommal mérést , úgy 5 * 2= 3 + 5 +2 = 10, azaz a rendszer éppen megoldható.

A kétszeres kölönbségek azt a mérési elrendezést modellezik, amikor ugyanabban az időben két szatellitára (j és k) végezzük a szimultán mérést az A és B pontokon, képezzük az előzőek szerint az egyszeres különbségeket majd kivonjuk öket egymásból:

T_B^k - T_B^j - T_A^k + T_A^j = (N_B^k - N_B^j - N_A^k + N_A^j + df_B^k - df_B^j - df_A^k + df_A^j).h

Megfigyelhetjük a modellnek azt a nagy előnyét, hogy az egyenletből kiesnek a vevők óra eltéréseit leíró ismeretlenek.

Ha itt is megvizsgáljuk a felírható egyenletek és ismeretlenek számát, úgy azt találjuk, hogy mivel egy kétszeres különbség egyenlethez két műhold szükséges, n_i számú műhold esetén egy időpillanatban (epochában) (n_i-1) egyenlet irható fel, n_t epochában tehát a felírható egyenletek száma (n_i - 1)*n_t. Az ismeretlenek száma pedig 3 koordináta ismeretlen és (n_i - 1) egész hullámszám ismeretlen. Azaz négy műhold esetén (n_i = 4) két észlelési időpontra (n_t = 2) van legalább szükség, ugyanis (4 - 1)*2 = 3 + (4 - 1) = 6.

A háromszoros különbségek képzéséhez két időpontban (t₁,t₂) képezett kétszeres különbségek különbségét képezik. Eredményként azt kapjuk, hogy

T_B^k(t₂) - T_B^j(t₂) - T_A^k(t₂) + T_A^j(t₂) - T_B^k(t₁) + T_B^j(t₁) + T_A^k(t₁) - T_A^j(t₁) =
(df_B^k(t₂) - df_B^j(t₂) - df_A^k(t₂) + df_A^j(t₂) - df_B^k(t₁) + df_B^j(t₁) + df_A^k(t₁) - df_A^j(t₁)).h

A háromszoros különbségek képzésének az a nagy előnye, hogy amint a fönti egyenletből látható nem csak az óra javítások hiányoznak belőle, hanem kiküszöbölődtek az egész hullámok számát leíró ismeretlenek is, és ennek következtében ez a modell érzéketlen az úgy nevezett 'ciklus csúszásokra', azaz arra a hibára ami az egész hullám számok változásának meghatározásakor következhet be, ha a vevő valamely akadály következtében ideiglenesen elveszti a kapcsolatot a műholddal.

A modell természetéből következik, hogy egy háromszoros különbség egyenlethez két észlelési alkalomra van szükség. Következésképpen n_t alkalom esetén
(n_t - 1) független észlelési időkombináció írható fel. n_i számú műhold esetén tehát az egyenletek száma (n_i - 1)*(n_t - 1) ennek kell nagyobb vagy egyenlőnek lenni 3-al a koordináta ismeretlenek számával. Ha 4 műholdra észlelünk, úgy az észlelési alkalmak száma legalább 2 kell hogy legyen mivel (4 - 1)*(2 - 1) = 3.

A GPS hibaforrásai

A méréstechnikában, igy a geodéziai mérésekben is megkülönböztetik a

véletlen hibákat vagy zajt, a
szabályos vagy szisztematikus hibákat és a
durva hibákat.

A GPS hibái e három forrás kombinációjából jönnek létre.

3.101 ábra - a GPS hibaforrások hatása

A 3.101 ábra jól illusztrálja a három hibatípus jellegét.
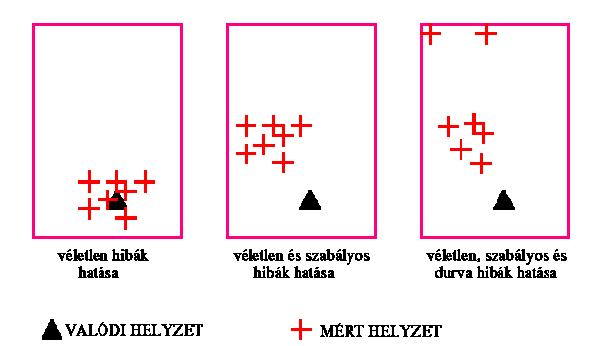
A zaj a valódi helyzet körüli szóródást idéz elő, végtelen sok mérés esetén a mérések átlaga a valódi helyzetet szolgáltatná.

A szabályos hiba minden mérést egy irányba torzít, a mérési szám növelésével az átlagban a torzítás értéke nem csökken.

A durva hiba a mérési pontosságot jelentősen meghaladja, szerencsére nem lép föl rendszeresen és a mérési szám növelésével az eredményekből kiszűrhető.

A véletlen hibák (zaj) főként a pseudovéletlen kód kb. 1 méteres zajából és a vevő szintén kb. 1 méteres belső zajából tevődnek össze.

· A szabályos hibákat a szelektív hozzáférés (SA) és más tényezők okozzák.

Ezek közül megemlítjük

A műhold órák azon hiba részét melyet a földi irányítóközpont nem korrigál. Ez az érték elérheti az 1 m.-t.
A műhold sugárzott koordináta hibái szintén 1 m. körüli értékek.
Az atmoszféra alsó 8 - 13 km.-es tartományában a troposzférában a jel terjedési sebessége függ az időjárási tényezőktől (hőmérséklet, légnyomás, páranyomás). Ha ezeket nem mérik és nem veszik figyelembe a számítás során, úgy 1 m.-es szabályos hibát okozhatnak.
Az ionoszféra, az atmoszféra 50 km.-től 500 km.-ig terjedő tartományának hatását a jel terjedési sebességére különböző modellekkel próbálják figyelembe venni. Mivel azonban ezek a modellek sem tökéletesek bizonyos esetekben 10 m. körüli szabályos hibával terhelhetik a mérést.
A GPS jel nem csak közvetlenül a műholdról, de különböző tereptárgyakról visszaverődve is bejuthat a vevőantennába. Mivel a visszavert jel hosszabb utat tesz meg mint a közvetlenül terjedő ez szabályos hibát eredményez, nagyságát 0.5 m.-re becsülhetjük.

A durva hibák több száz kilométeres eltéréseket is eredményezhetnek

A földi ellenőrző rendszer számítógépes vagy emberi hibái egy métertől több száz kilométerig terjedő hibákat okozhatnak.
A felhasználók, főként a rossz dátum beállítással, 1 m.-től több száz méterig terjedő eltéréseket idézhetnek elő.
Ha a vevők hardvere vagy szoftvere elromlik, tetszőleges nagyságú hiba bekövetkezhet.

Tipikus az az eset, amikor a véletlen és szabályos hibák kombinációjaként minden a pontmeghatározásban résztvevő szatellitára 15 m. körüli távmérési hiba adódik.

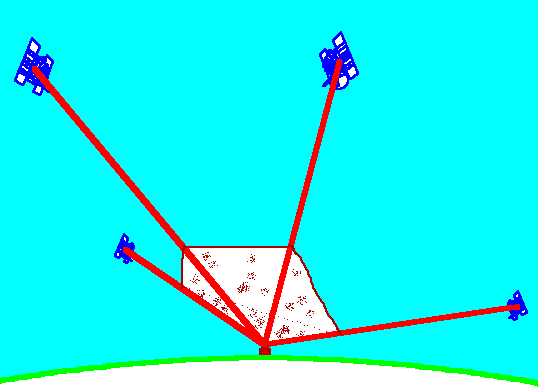
Eddig mérési hibákról beszéltünk, a mért távolságokból azonban a bevezetőben vázolt geometriai elv (három gömb metszése) felhasználásával koordinátákat akarunk meghatározni. Ha a metsződő gömbök sugara hibás, úgy a koordináta meghatározás pontosságát befolyásolja a pontról a műholdakra irányuló vektorok kölcsönös helyzete.

E geometriai hatás figyelemebe vételére a GPS-szel foglalkozó szakterület a GDOP nevű mennyiséget használja. A GDOP betűszó a Geometric Dilution of Precision (geometriai pontosság hígulás) angol kifejezés rövidítése.

3.102 ábra - rossz GDOP

3.103 ábra - jó GDOP

Meghatározás szerint a GDOP fordítva arányos a meghatározandó pontról a műholdakra menő irányok egységvektorai által határolt gúla köbtartalmával.

Ha tehát a gúla köbtartalma kicsi, következésképpen a GDOP nagy, a helymeghatározás pontossága pedig alacsony (3.102 ábra). A fordított esetben, amikor a gúla köbtartalma nagy, a GDOP pedig kicsi, a pontmeghatározás pontossága megnő (3.103 ábra).

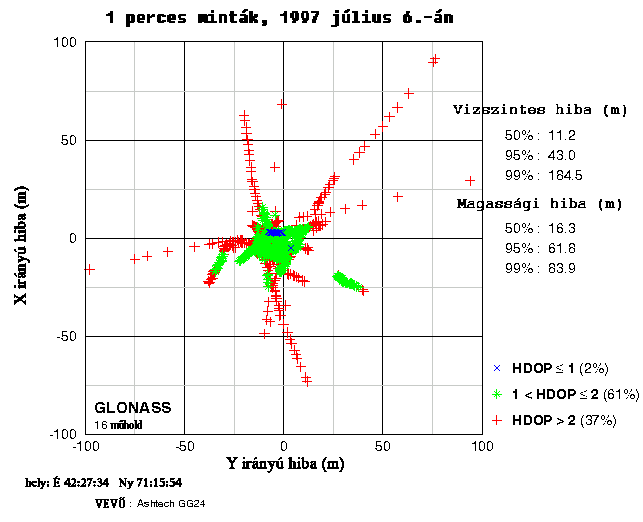
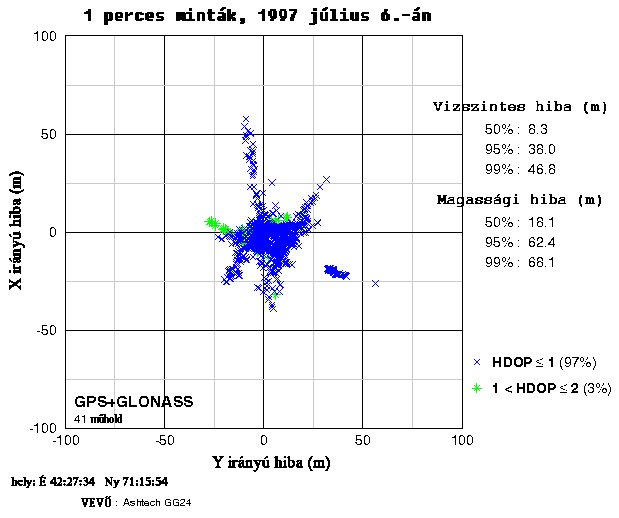
Talán meggyőzőbb a hibák szóban történő kifejtésénél a mérési eredmények grafikus ábrázolása. A következő három ábrát a MIT Lincoln Laboratórium munkatársai készítették a közelmúltban készült méréseik alapján. Az ábrákhoz összességében csak annyi magyarázatot kell hozzátenni, hogy a GDOP felbontható vízszintes és magassági komponensre, az ábrákon szereplő HGDOP a vízszintes komponens.

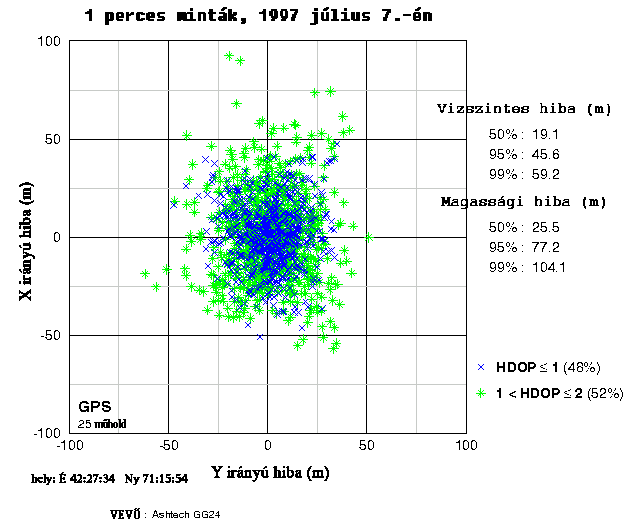
3.104 ábra - 1 perces GPS mérési minták pontossága

A 3.104 ábra nagyon jól illusztrálja a véletlen hibák megjelenési formáját. Az ábrán jól követhető, hogy a kisebb tehát pontosabb HGDOP-pal rendelkező, kékkel jelölt mérések nagyon jól tömörödnek az elméleti ponthely környezetében.
Érdemes megfigyelni, hogy míg a vízszintes hiba 99%-os valószínűségi színten 59.2 m.-en belül van, addig a grafikusan fel nem tüntetett magassági hiba ugyanezen a valószínűségi színten 104.1 m., azaz a vízszintes hibának majdnem a kétszerese.

A 3.105 ábrán a GLONASS mérési eredményeket vehetjük szemügyre. Az első figyelmet érdemlő tény, hogy a 25 GPS műholddal szemben az észlelési időpontban csak 16 GLONASS műhold működött. Ennek következtében egyrészt jelentősen csökkent az 1-nél kisebb HGDOP-pal rendelkező mérések száma, másrészt megjelentek a 2-nél nagyobb HGDOP értékek is. Az ábra egyértelműen bizonyítja, hogy azonos HGDOP értékek esetén a GLONASS mérések sokkal pontosabbak. Másik érdekes jelenség, hogy a GLONASS magassági hibája nem tér el szignifikánsan a vízszintes hibától.

3.105 ábra - 1 perces GLONASS mérési minták pontossága

A 3.106 ábra az optimális mérési módszer, a közös GPS - GLONASS mérések pontosságát mutatja be. Az ábra legfőbb mondanivalója, hogy az esetek 97%-ában a HGDOP kisebb volt egynél, azaz a két rendszer együttes konstellációja szinte minden időben biztosítja az optimális geometriai elhelyezkedést az észlelt műholdak és az álláspont között. Ennek megfelelően jelentősen nőtt a pontosság nem csak az önálló GLONASS észleléshez képest, de az önálló GPS észleléshez képest is. Különösen jelentős a magassági hiba csökkenése, mely kb. 80%-os a GPS mérésekhez képest.