Megjelenítési funkciók II

Ezen a lapon befejezzük a megjelenítés kérdéseit miután áttekintjük

Felület árnyalás.

A 90-es évek előtt az árnyalás (szakmai zsargonban színtörlés vagy 'sauberolás') kifejezéseket leginkább csak a topográfusok és kartográfusok használták, napjainkban ugyanezt a fogalmat 'rendering' alakban már az AUTOCAD használóinak széles tábora ismeri.

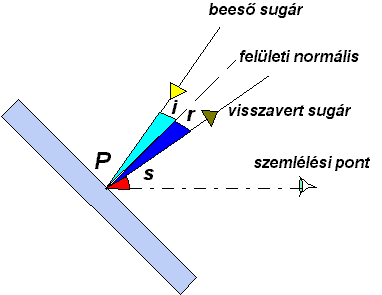
Az árnyalás azt a fizikai tényt modellezi a felületek élethű megjelenítésére, hogy a természetben található felület elemek a megvilágítás, a térbeli helyzet, a visszaverő anyag minősége és a szemlélési pont elhelyezkedése függvényében különböző fényességgel látszanak.

Esetenként a felsorolt tényezők több paraméterrel is befolyásolják az eredő fényességet, melyek megadását a szoftverek gyakran igényelhetik ezért indokolt, hogy röviden áttekintsük ezeket a paramétereket és bemutassuk a fényességre gyakorolt hatásukat.

A megvilágítás szórt (diffúz) vagy pontból kiinduló sugaras lehet.

A diffúz megvilágítás következtében fellépő árnyaltság független a felület elem térbeli helyzetétől és csak a fény erősségétől és az elem visszaverési tulajdonságaitól függ. Ebből következik, hogy ez a megvilágítás önmagában alkalmatlan a felület plasztikus megjelenítésére, ugyanakkor kiegészítő megvilágításként alkalmazva hasznosan csökkentheti a mesterséges látvány hatását keltő túlzott kontrasztot.

A sugaras megvilágításnál feltételezzük, hogy a megvilágító pont a végtelenben van, s ezért minden beeső fénysugár párhuzamos. A felületelem sugaras megvilágításból eredő fényessége függ a beeső sugár és a felületelem szögétől. Akkor lesz az elem a legfényesebb ha a sugár merőleges a felületre, a felülettel párhuzamos megvilágítás esetén az elem sötét marad.

Amint azt az előző bekezdésben már láttuk a felületelem térbeli helyzete (azaz síkjának szöge a megvilágító fénysugárral) befolyásolja az elem fényességét. Ez a fényesség tulajdonképpen azt jelenti, hogy az elem visszaveri a fényt, ez a visszaverődés azonban az esetek többségében túlnyomóan diffúz.
Teljesen diffúz visszaverődés esetén a szembe jutó fényenergia mennyisége, hasonlóan a diffúz megvilágítás okozta fényességhez, független a szemből az elemre bocsátott sugár szögétől. Tükrös visszaverődés esetén elvileg a szembe nem juthat fény, ha a szem-felület sugár nem esik egybe a tükrözött sugárral. Gyakorlatilag azonban a mindig fennálló diffúz visszaverődés következtében, amint azt látni fogjuk, ezt az esetet visszavezetik a kvázi diffúz visszaverődés esetére.

A visszaverő anyag minősége is többféleképpen befolyásolja az eredő fényességet. Diffúz visszaverődés esetén anyagjellemző az Rd visszaverődési (reflexiós) tényező, mely színfüggő, azaz minden színtartományhoz más és más az értéke (ezen a fizikai tulajdonságon alapul a passzív multispektrális távérzékelés). Részben az anyagminőségtől, részben az i beesési szögtől függ a W(i) tükrözési együttható, mely a tükrözéssel visszavert fényenergia mennyiséggel arányos.
Bár a térinformatikában nincs jelentősége, a teljesség kedvéért megemlítjük, hogy az anyagok fényáteresztők is lehetnek s ebben az esetben az áteresztett fényenergia a T áteresztési tényezővel arányos, mely szintén az anyag minőségétől függ.

Kvázi diffúz visszaverődés esetén, tehát abban az általános esetben amikor a felület diffúz visszaverését bizonyos mértékű tükrös visszaverés is módosítja, a szembe jutó Eps fényenergia az alábbi közelítő képlettel számítható:

 

(33),

ahol Ips a fényforrásból a visszaverő pontba érkező sugaras fényenergia, az i és s szögek értelmezését pedig a 4.44 ábra szemlélteti.
Ha diffúz megvilágítás is van, úgy az abból visszavert fényenergia hozzáadódik (33) értékéhez. Ebben az esetben tehát

 

(34),

ahol Epd a pont diffúz megvilágításából diffúzan visszaverődő fényenergia, Id pedig adiffúz megvilágítás energiája.
4.44 ábra - a szögek értelmezése a fény visszaverődésekor

Amint látjuk a megvilágítás erőssége nagymértékben függ a felületelemnek a megvilágítási és szemlélési pontokhoz viszonyított helyzetétől, melyet az i és s szögek fejeznek ki. A (33)-ban és (34)-ben szereplő n kitevő értéke 1 és 10 között változik. Minél simább a felület annál nagyobb szerepe van a direkt tükrözésnek következésképpen n értéke annál nagyobb, fordítva matt felületek esetén kis n értékeket állítanak be a szoftverek.

A felület milyenségét a szoftvereknek rendszerint beállító dobozok kitöltésével adja meg a felhasználó.

Azonos anyagminőség, megvilágítási irány, sugaras illetve sugaras és diffuz megvilágítási energia esetén a visszavert fény csak a felületelem elhelyezkedésétől azaz a felületi normális irányától függ. Mivel a terepet a DEM és TIN modellek sík négyzet illetve háromszöglapokkal modellezik ez azt eredményezi, hogy a lapok élein a (33) illetve (34) képletekből számítható megvilágítottság ugrásszerűen változik, ami durva felbontás esetén előnytelen, természetellenes látványt eredményezhet. Ezt elkerülendő, a síklap sarokpontjainak normálisát a sarokpontban metsződő lapok normálisainak átlagaként határozzák meg, kiszámítják e pontok fényességét, majd a sarokpontok fényességét az érintett oldalak mentén lineárisan interpolálják. A lapok belsejében lévő pontok fényességét pedig metszetek mentén interpolálják a metszet oldalakból kimetszett fényességértékeire támaszkodva.

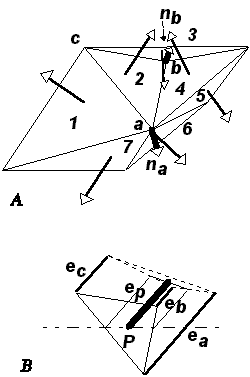
A 4.45 ábrán megpróbáltuk felvázolni az elmondottakat.

Az ábra A részén a 2 háromszög a és b sarokpontjaira megrajzoltuk a sarokpontokban csatlakozó lapok normálisainak átlagából levezethető na és nb átlagos normálisokat (mivel helyszűke miatt a c pontban találkozó valamennyi háromszöglapot nem tudtuk megrajzolni azért nc-t sem tüntettük fel a rajzon.

Az ábra B részén felraktuk az a, b, c pontokban az átlag normálisokból számítható fényességet és a lineáris interpoláció grafikus felvázolásával meghatároztuk valamely lapon fekvő P pont fényességét.

4.45 ábra - fényességi értékek interpolálása

 
4.46 ábra - réz csonka kúp árnyalása AutoCAD-ben

4.47 ábra - tájkép árnyalása AltaVista program-demóban

A 4.46 ábrán megpróbáltuk az árnyalást egy szabályos tárgy (esetünkben egy csonka kúp) bemutatásával szemléletesebbé tenni. Sajnos a szövegszerkesztő grafikus szűrője nem túl meggyőzően támogatta ezt a törekvésünket.

A 4.47 ábrán pedig egy terepszakasz öszi képét látjuk madártávlatból. A reprodukció itt sem túl sikeres, de talán képes arra, hogy szemléltesse a fentiekben vázolt száraz elméleti meggondolásokat.

 

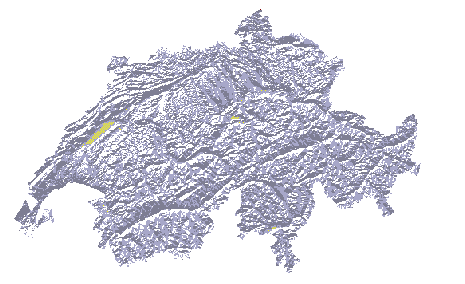
Az árnyalás jelentőségét legjobban talán a 4.49 ábrán látható domborzati térkép szemlélteti. Az ábrán a svájci domborzat lejtőirányainak (aspekt) kihangsúlyozására használják az árnyékolást.

4.48 ábra - Svájc domborzati térképe

Nem igényel külön magyarázatot, hogy egy ilyen ábrázolás még a laikusok számára is értelmezhetővé teszi azokat a felszíni formákat, melyeket szintvonalas domborzatábrázolás esetén még a szakembereknek sem könnyű rövid idő alatt áttekinteni

 

Még egy új dologra is felhívja a figyelmünket a megelőző két kép: a színek szerepére a szemléltetésben. Mivel ez a téma a hardver feltételek fejlődésével egyre nagyobb gyakorlati jelentőségre tesz szert a következő pontban röviden összefoglaljuk a színekre vonatkozó elvi és technikai kérdéseket.

A színek szerepe a megjelenítésben.

Ha a színek szerepét vizsgáljuk a megjelenítésben, akkor két oldalról közelíthetjük meg a kérdést:

  1. Az alkalmazott színek vizuális hatásának - jelentésének oldaláról;
  2. A kiválasztott színek számítógépen történő technikai realizálásának oldaláról.

Az első szempont vizsgálatakor döntő jelentőségűek a topográfiai és tematikus térképezés hagyományai. A hagyományok figyelembevételénél azonban nem szabad elfelejteni, hogy a térképek nyomdai előállítását jelentősen bonyolította és a színek számától függően drágította a többszínnyomás, minek következtében a kartográfusok kénytelenek voltak az alkalmazott színek számát a minimálisra csökkenteni.

A legáltalánosabban elfogadott hagyományos színsorozattal a rétegszínezésben - a domborzat hypszometrikus ábrázolásában találkozunk.
Ezek szerint, ha a domborzatot, tengerek esetén a tengerfenék formáit magasság szerint (a tengerfenék mélységét negatív magasságnak tekintve) osztályokba soroljuk, úgy az alkalmazott színskála a tengerek esetében a sötétkéktől a világoskékig (a legmélyebb a legsötétebb), szárazföldek esetén a sötétzöldtől a világoszöldön, sárgán, világosbarnán, sötétbarnán keresztül a vörösig (néha fehérig vagy rózsaszínig) tart. Érdemes megemlíteni, hogy a szárazföld tengerszíne alatti részeit is sötétzölddel (és nem világoskékkel) ábrázolják. Ez utóbbi tény valamint az a már említett körülmény, hogy a havasokat a sötétbarnát követően nem sötét hanem világos színnel jelölik tulajdonképpen azt mutatja, hogy ezek a domborzati térképek a magassági ábrázolás mellett a felszín bizonyos jellemzőit tematikusan is ábrázolják.

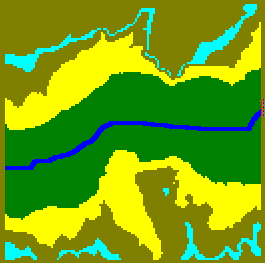
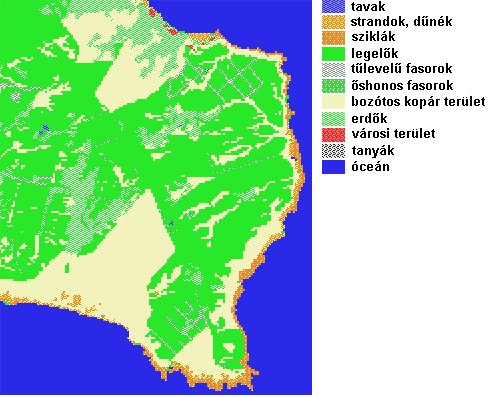
Ez az állításunk még inkább megerősödik ha az általános iskolából jól ismert hegy és vízrajzi térképekre gondolunk, melyeken magasságuktól független egységes kék színnel jelennek meg a folyók és tavak.

A 4.49 ábrán a rendelkezésre álló színek (paletta) felhasználásával megpróbáltunk bemutatni egy sziklás vidékkel körbevett völgyet, és a völgyben elhelyezkedő folyót.

4.49 ábra - domborzatszínezés

Az elfogadott színhozzárendelések egyöntetűsége csökken az úgynevezett földhasználati rétegek színezésekor. Ez több dologgal is magyarázható.
A hagyományos topográfiai térképek, melyek először ábrázolták egységesen a földhasználat bizonyos elemeit (domborzati idomok, úthálózat, vizek, bokros területek, legelők, kertek, szántók, erdők építmények, stb.) igyekeztek a rendelkezésre áll színeket úgy hozzárendelni, hogy azok valamilyen kapcsolatban legyenek a kérdéses objektumok vizuális megjelenésével. Példaként említhetjük az erdők zöld színét, a vizek kék színét, illetve az éghetetlen anyagokból készült épületek vörös színét. Bár az utóbbi esetben a kapcsolat a szín és a vizuális benyomás között nem annyira kézenfekvő, a kapcsolat mégis fölfedezhető, ha arra gondolunk, hogy a tűzálló anyagok közül leggyakrabban téglát alkalmaztak házépítésre.

A többcsatornás távérzékelés megjelenésével azonban nem csak bővült a földhasználati fedvények bizonyos objektumainak osztályozási lehetősége (növényzet, talajtípusok, stb.), de az úgynevezett hamis színes kompozitokon a paletta is megváltozott (pld. az egészséges vegetáció élénk vörös, a betegségekben szenvedő halvány rózsaszín) elsősorban a tematikus térképezésben megszokott azon elvek alapján, hogy a kiemelendő foltokat élénken kell megjeleníteni és erős kontrasztot kell alkalmazni a megkülönböztetendő osztályok között. Ha ehhez hozzátesszük, hogy a számítógép nyújtotta lehetőségek megsokszorozták a földhasználati fedvények lehetséges variánsait, úgy nem meglepő, hogy e területen már nem beszélhetünk egységes színezésről. Ha sommásan akarjuk összefoglalni a jelenlegi helyzetet, úgy azt mondhatjuk, hogy a regionális tervezők inkább a vizuális benyomásokat tükröző térképezés hagyományait kivájnák továbbfejleszteni, míg egy egy szűkebb jelenség globális vizsgálatakor a természettudósok inkább a távérzékelési gyakorlat színezési módszereire támaszkodnak.

A 4.50 ábrán az előbbire mutatunk be egy ausztrál példát. A földhasználati fedvényt arra használták, hogy új üdülőtelepet tervezzenek Sidney környékén. Amint az ábrából látható, a természetes színhatás alkalmazása mellett a kartográfus vonalkázási minták segítségével igyekezett megkülönböztetni az azonos színű de más objektumhoz tartozó elemeket.

A színek és vonalkázás összekapcsolása egyértelműen arról tanúskodik, hogy a térkép alkotója topográfiai térképezési hagyományon nevelkedett.

 
4.50 ábra - földhasználati térkép színezése

 

A népességi, gazdasági, kulturális, stb adatokat tartalmazó fedvények a dolog természetéből adódóan nem alkalmazhatják azt az elvet, hogy a fedvény színezése tükrözze a valóság vizuális felfogását, hisz pld. a egy ország népsűrűsége nem vált ki a szemlélőből semmilyen színhatást. Ebben az esetben a színekkel valamely jelenség számokban kifejezett értékét kívánjuk kódolni.

Jól szemlélteti a jelenséget ha a számok növekedését vagy csökkenését a "természetes színskálához" rendeljük. Ezt a növekedést vagy csökkenést avval is még plasztikusabbá tehetjük, ha a változás ütemében nem csak a színeket, hanem azok fényességét is valamilyen irányban szisztematikusan változtatjuk. A későbbiekben a HSV színmodell ismertetése kapcsán megismerkedünk mind a természetes színskála létrejöttével, mind pedig a fényesség paraméterével. Egyelőre elég annyit tudnunk, hogy a színek ebben a modellben a következőképpen jönnek egymás után: sárga, zöld, encián, kék, bíbor, vörös.
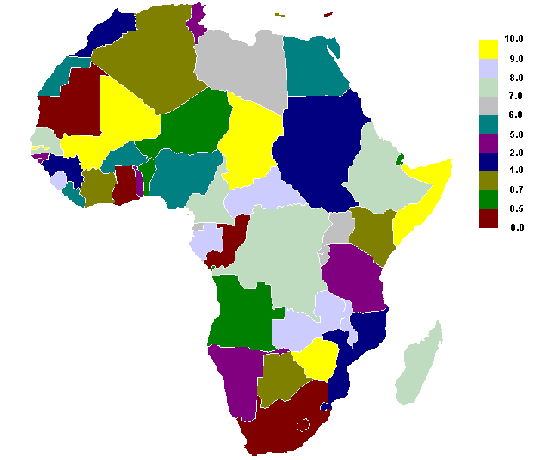
4.51 ábra - intervallumok megfeleltetése színeknek

A 4.51 ábrán egy afrikai modellkísérlet eredményeit mutatjuk be a fenti elvek alapján (a legnagyobb értékhez rendeltük a sárga színt az alkalmazott legnagyobb fényességgel, a legkisebbhez pedig a vörös színt az alkalmazott legkisebb fényességgel).

Még egyszerűbb a helyzet azokban a gyakorlati esetekben, amikor az objektumokat rangsor nélkül kívánjuk megkülönböztetni, pld. ha csak az országokat kívánjuk megkülönböztetni Afrika térképén. Ebben az esetben arra kell törekednünk, hogy lehetőleg minden ország különböző színnel kerüljön ábrázolásra. ha ez nem lehetséges, úgy legalább azt el kell érnünk, hogy egymással határos országok ne legyenek azonos színűek. Ezenkívül még gondoskodnunk kell arról is, hogy az egész térkép megjelenése esztétikus legyen.

Szólnunk kell végül a szinek alkalmazásánál a funkcionalitás szerepéről is. A színek elsődleges szerepe, hogy azonnali vizuális megkülönböztetést, esetleg osztályba sorolást biztosítson a felhasználónak. A második szempontról már szóltunk. Az első szempont viszont azt kívánja, hogy az objektum színe jól megkülönböztethető legyen, ez pedig a háttérhez való viszonyától és kiterjedésétől függ. Nagy foltszerű objektumok esetén bátran alkalmazhatunk kis kontrasztot (különbséget a háttértől illetve a szomszédoktól) ha ezt valamilyen tematikus ok (pld. természetes színsor megfeleltetés) indokolja. Vonalas objektumok pld. utak, határok stb. esetén azonban ez megengedhetetlen. Hogy ez a figyelem felhívás különösen a számítógépes szakemberek számára nem felesleges azt jól bizonyítja néhány GIS demó, melyek tervezői pld. az utakat sötétbarnával jelölik a fekete háttéren, s minél fontosabb az út annál kevesebb színnel (szaggatott vonal, eredmény vonal, stb.). Hogy nem mutatom be ezeket a negatív példákat az csak azért van, mert az olvasó nyomtatási lehetőségeimnek tudná be, hogy nem lát semmit.

A vizuális kérdések áttekintése után térjünk rá színek számítógépes előállításának technikai kérdéseire.

Természetesen nem fogunk foglalkozni sem a hardver sem a szoftver részleteivel, alapvetően azt szeretnénk elérni, hogy a felhasználó megismerkedjen azokkal a lehetőségekkel amelyekkel színeket választhat, s hogy a választása olyan legyen amilyent elképzelt. A számítógépes színgenerálás azon a fizikai tényen alapul, hogy különböző erősségű vörös, zöld és kék szín összeadásával az összetevők megfelelő aránya esetén tetszőleges szín létrehozható. Ezt a rendszert, mivel az alapszínek összeadásával generálja a színeket additív színgeneráló rendszernek nevezik. Az alapszínek angol neveinek (Red, Green, Blue) kezdőbetűi alapján a rendszert gyakran egyszerűen RGB rendszernek is hívják.

A számítógép képernyőjén három réteget alkalmaznak, melyeket külön-külön elektronágyúk gerjesztenek. Az elektron sugárzás hatására a rétegek ugyanazon a képelem területen vörös, zöld és kék fényt bocsátanak ki, melyek összeadódva generálják a kérdéses pixel színét. Az, hogy az elektronágyúk hány erősségi fokozatban képesek kiváltani az alapszíneket attól függ, hogy a grafikus kártya hány bitet biztosít az egyes elektronágyúk vezérlésére. A jól ismert EGA kártya két-két bitet használ e célra s ez azt eredményezi, hogy a megjelenítendő szín 64 szín közül választható. A VGA és az IBM 8514/A kártyák ugyan e célra hat-hat bitet tartalékolnak s e miatt a megjelenítendő szín 262144 színből választható.

A képernyővezérlők másik pamétere egy képpont tárolására szolgáló bitek száma. Ettől függ ugyanis, hogy egyidejűleg hány szín jeleníthető meg a képernyőn. Az egyidejűleg megjeleníthető színeket palettának hívják. Az EGA és VGA négy biten tárolja a képpontokat így egyidejűleg 16 szín megjelenítésére képesek, az IBM 8514/A esetében minden pixelhez nyolc bitet rendelnek s így a palettában szereplő színek száma 256.

A korszerűbb (pld. S3 típusú) grafikus kártyák esetében bizonyos határokon belül szabadon programozható a színskála, paletta és a felbontás (a megjeleníthető oszlopok és sorok száma), mivel a grafikus memória összterülete nem változhat, több szín, nagyobb paletta kisebb felbontást von maga után. Amint láttuk a palettát még az EGA esetében is több színből kell kiválogatni. A GIS, CAD és egyéb grafikus programok rendszerint rendelkeznek egy vagy több előregyártott palettával, de a jobb programok felhasználói paletták létrehozását is lehetővé teszik, sőt az újabbak amint erre később rátérünk még segítik is a paletta generálást.
4.52 ábra - a képernyőn és a nyomtatóban alkalmazott színrendszerek

Míg a képernyőn a színek összeadás eredményei, addig a nyomtatók, mivel fehér papírra dolgoznak három alapszínt megvalósító festékkel, úgynevezett szubtraktív rendszerben, kivonással hozzák létre a színeket. Az alkalmazott alapszínek ebben az esetben az encián (Cyan), bíbor (Magenta) és sárga (Yellow), s ezért e rendszert CMY rendszernek is hívják.

Az alapszínek erőssége ebben az esetben a kérdéses festékréteg vastagságától függ.
Az elmondottak illusztrálására a 4.52 ábrán bemutatjuk az additív és szubtraktív színgenerálás alapelvét.

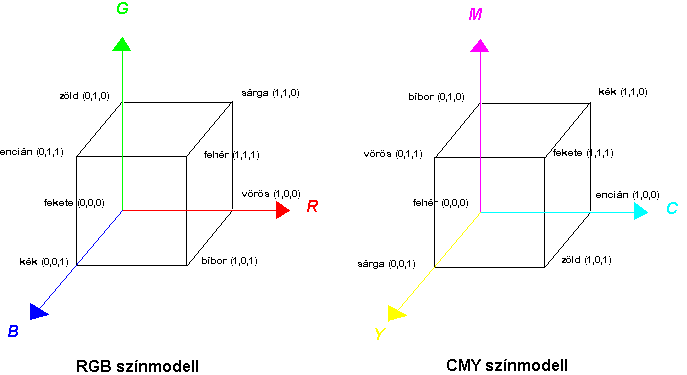
Mind az RGB mind a CMY színmodellt olyan egységkockával szokták ábrázolni, mely egy térbeli derékszögű koordináta rendszer első térnegyedében helyezkedik el. A kockákon belül elhelyezkedő minden pont egy-egy színnek felel meg, mely a pont R,G,B illetve C,M,Y koordinátáiból keverhető. A koordináták 0 - 1 között változhatnak, amely százzal szorozva a kérdéses szín maximumának %-át jelenti. Ha tehát pld. 64 színfokozatunk van és R=67%, G=28%, B=9% ez azt jelenti, hogy a szükséges elektronsugár vezérlési értékek R=42, G=18, B=6, (bizonyos programok lehetővé teszik a százalékban való beállítást is). A fentiek illusztrálására a 4.53 ábrán bemutatjuk a kockamodelleket.
4.53 ábra - RGB és CMY kockamodellek

Az ábrából jól látható, hogy a kocka csúcspontjain elhelyezkedő színeken kívül, megfelelő gyakorlat nélkül szinte lehetetlen megsaccolni, hogy a választott vörös zöld és kék összetevők keverése milyen színt fog eredményezni. Talán az egyetlen szabály, amit a kockával kapcsolatban érdemes elmondani az az, hogy két szín közötti folyamatos átmenetet a két színpontot összekötő egyenesen való haladás biztosítja.

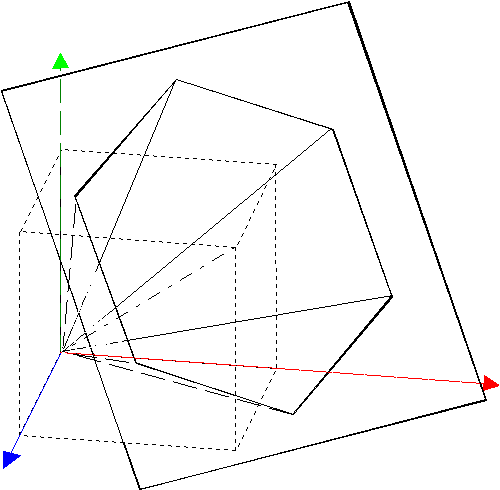
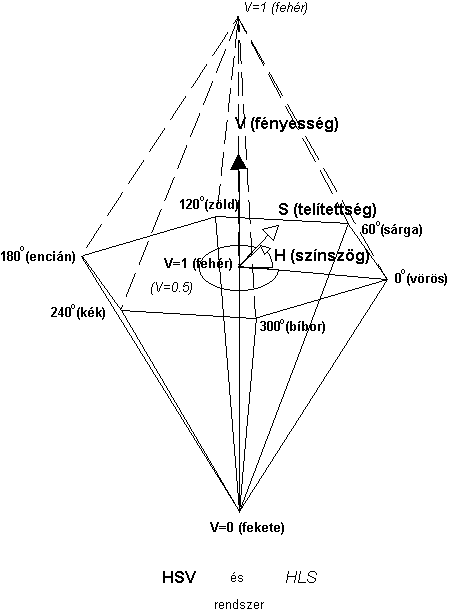
4.54 ábra - a HSV modell származtatása az RGB kockamodellből

A 4.54 ábrán felvázoltuk a felhasználóbarátabb HSV (Hue=színszög, Saturation=telítettség, V a fényességet jelöli, de a Value=érték rövidítése) származtatását az RGB modellból. Szerkesszük meg az RGB kocka Fekete-Fehér átlóját és a fehér pontban helyezzünk el egy az átlóra merőleges síkot. Vetítsük fel a kocka maradék hat csúcspontját merőlegesen a síkra és a nyert szomszédos pontokat kössük össze. A nyert hatszöget tekintsük egy gúla alapjának, melynek csúcspontja a kocka fekete pontja. A nyert modellt most már önállóan is ábrázolhatjuk a 4.55 ábrán.

 

Ha a HSV rendszer gúláját tükrözzük az alaplapjára és az alaplaphoz V=0.5 értéket rendelünk, úgy a az úgynevezett HLS rendszert kapjuk, melyet szintén ábrázoltunk a 4.55 ábrán. A két rendszer között az a leglényegesebb különbség, hogy az ábrázolt alapszínek kiválasztása a fényességi skála maximumán (HSV) vagy közepén (HLS) történik-e.


A modellel kapcsolatban három dolgot kell megjegyeznünk:

1.     Látható az ábráról, hogy mind a színt (H), mind az élénkséget (S), mind pedig a fényességet (V) közvetlenül vezérelhetjük.

2.     A gúla a kocka bonyolult leképzése, következésképpen nem lehet egyszerű módon a két rendszer közt átszámolni, ezt az átszámítást a jobbminőségű grafikus programok biztosítják.

 

3.     A programok annak a fügvényében állapítják meg H, S és V beállítási egységeit, hogy az R G és B hány fokozatú, mégpedig olymódon, hogy az előbbiek állítási értékei nagyságrendileg megegyezzenek az utóbbiakéval.

4.    

4.55 ábra - a HSV és HLS modell

Ezek után már nincs más feladatunk, minthogy a PSP program beállító ablaka segítségével bemutassuk miként segítik a korszerű grafikus szoftverek a paletta színeinek beállítását.
4.56 ábra - színválasztó panel

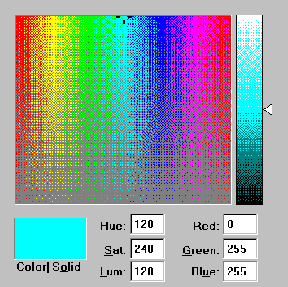
A 4. 56 ábrán az encián színt rendeltük a paletta egy kiválasztott sorszámú színtartójához (a kérdéses paletta az előző lépésben jelent meg, s nekünk kétszer kellett kattintani arra a színtartóra, melyet meg akarunk változtatni).

Az ábrából látható, hogy az RGB állítási lehetőség 256 fokozatú (0-255), míg a megfelelő HLS értékek 0-240 között változnak (pontosabban a H 0 és 239 között változtatható).

 

Ha az ábra jobboldalán lévő nyilat felfelé toljuk úgy a szín egyre világosabb lesz (L értéke növekszik) míg az ábra tetején el nem éri a fehér színt, ekkor L=240. A fehér szín megjelenése független attól, hogy H és S milyen értékekre vannak beállítva.
A baloldali nagyobb színes négyzet felső középső részén látható a beállító kurzor mely vagy az egérrel vagy a H és S értékek bebillentyűzésével mozgatható. A négyzetben H felel meg a vízszintes, S pedig a függőleges koordináta tengelynek.

A beállítások RGB értékekben is elvégezhetők. A három beállítási lehetőség szinkron működik, azaz ha pld. egérrel mozgatjuk a kurzort és a nyilat a megfelelő értékek mind a HLS mind az RGB skálán megjelennek és viszont ha valamelyik skálán beállítási adatokat viszünk be a másik skála is megjelenteti a kérdéses szín paramétereit valamint a kurzor és a nyíl is a skála által meghatározott helyre megy.

Mielőtt a színek tárgyalását lezárnánk fel szeretnénk hívni az olvasó figyelmét arra, hogy néhány GIS szoftver, illetve szoftver verzió nem teszi lehetővé a paletta szabad beállítását, vagy ha ez a lehetőség meg is van a beállítás csak a kényelmetlenebb RGB rendszerben lehetséges.

Az első esetben egyszerű eszközökkel nem igen tudunk mit tenni, ezért az ilyen szoftverek használatát lehetőleg kerüljük. A második esetben előbb célszerű valamely felhasználó barát szoftver segítségével létrehozni a kívánt palettát, kiírni az RGB beállítási értékeket, majd bebillentyűzni azokat a használt GIS szoftverbe.

ˇ         a következő részben a szakértői rendszerek bemutatásával befejezzük a tényleges és potenciális GIS funkciók tárgyalását

ˇ         esetleg visszatérhet az előző részhez

ˇ         illetve a tartalomjegyzékhez

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc