Ebben a részben a raszteres adatokkal végezhető számítások közül megismerkedünk:
Már a vektor-raszter konverzió kapcsán utaltunk rá, hogy a különböző műveletek végrhajtására nem egyformán előnyös a két adatmodell. E tétel illusztrálására célszerű, ha áttekintjük az elemi műveletek végrehajtásának főbb momentumait raszteres adatmodell esetén is. A kérdés vizsgálatakor arra is figyelemmel kell lennünk, hogy a raszteres adatok milyen formáját alkalmazhatjuk célszerűen a műveletekhöz. Nem közömbös ugyanis, hogy a kérdéses művelet elvégezhető-e gazdaságosan valamely tömörített formában (ilyenkor rendszerint a quadtree struktúrára gondolunk), vagy pedig a művelet elvégzéséhez előbb ki kell bontani a tömörített struktúrát, majd a művelet elvégzése után az eredményt ismét tömöríteni kell.
Távolságfogalmak, koordinátákkal adott pontok megkeresése
Az Euclides-i illetve Manhattan távolságfogalmak a raszteres adatmodellekben is használatosak. Kizárólag ezekben kerül ugyanakkor alkalmazásra, a quadtree középtengely transzformációval kapcsolatban implicit módon már bevezetett, és az alábbi kifejezésel értelmezett sakktábla távolság:
A sakktábla távolság tehát nem más, mint a két pont abszolút értékre nagyobbik koordináta növekménye.
A legegyszerűbb raszteres alapművelet valamely koordinátáival adott pixel tulajdonságjellemzőjének (szinének) a megkeresése. Mátrixban tárolt raszterkép esetén ez egy hozzáféréssel elvégezhető. Quadtree tárolás esetén a feladat megoldása egy kissé bonyolultabb. A gyökér csomópontból kiinduló algoritmus először összehasonlítja a pont koordinátáit a gyökér középpontjának koordinátáival. Ha például mindkét koordináta kisebb a középpont koordinátáinál, úgy a keresést a harmadik él mentén a Délnyugat-i negyedben kell folytatni. A folyamat rekurzív módon mindaddig ismétlődik, míg a keresés el nem jut a pontot tartalmazó levélig. A levél színe (fekete vagy fehér) meghatározza a pont színét is.
Az idom(ok) kerületének meghatározása
Míg a kerület meghatározás a vektoros modellekben a legegyszerűbb műveletek közé tartozik, addig a raszteres modellekben e műveletet eleve bonyolítja, hogy háromféle raszteres kerület meghatározás is létezik, melyek közül kettő két-két alvariánsban is használatos.
Belső kerületnek nevezzük azoknak a fekete pixeleknek a számát, amelyek d- vagy i-szomszédosak fehér pixelekkel. Hasonlóképpen, külső kerületnek azoknak a fehér pixeleknek az összegét nevezik, melyek d- vagy i-szomszédosak fekete pixelekkel. Számunkra leghasználhatóbb a határoló kerület fogalma, mely meghatározás szerint, a d-szomszédos fehér és fekete pixelek határvonalai összegeként számítható. További vizsgálódásaink során kerület szóval a határoló kerületet jelöljük.
Legegyszerűbben a lánckódban tárolt bináris kép kerületét tudjuk kiszámolni, ezért gyakran a quadtreeben tárolt képet is előbb lánckódba konvertáljuk, majd a kerületet a lánckód felhasználásával számítjuk ki. A kerület a lánckódokból gyakorlatilag közvetlenül meghatározható, hiszen csak a rekord második mezejétől kezdődően a mezők második elemeit kell összegezni. A 2.12 ábra példáján a kerületet a következő összeg
A kerületet közvetlenül quadtreeből számító algoritmus úgy dolgozik, hogy előre meghatározott sorrendben (például balról jobbfelé haladva) sorraveszi a fa ágait és amint fekete levélre talál megvizsgálja, hogy milyen a fekete levél nyugati és északi szomszédjának színe. Ha azt találja, hogy a szomszéd fehér, úgy a talált fehér szomszédok számát (egyet vagy kettőt) megszorozza a figyelembe vett fekete levél oldalhosszával és hozzáadja a kerületet alkotó részösszeghöz. Miután a program minden ágon végighaladt a részösszeg a fél kerületet fogja szolgáltatni mivel a program csak a lehetséges szomszédok felét vizsgálta.
|
Ahhoz hogy a kép szélén lévő fekete pixelek is kényelmesen figyelembe vehetők legyenek a kerület összeszámolásában célszerű a képet a 2.43 ábrán látható módon északi és nyugati határai mentén egy színttel magasabb fehér quadtreebe beágyazni. Ha a beágyazás után a kép felbontását nem változtatjuk meg, azaz feltételezzük, hogy a négyszer olyan nagy kép is ugyanannyi pixelre van osztva mint az eredeti, úgy a pixelek oldalhossza képzetesen kétszeresére nő, és ezért a végösszeg nem a fél, hanem az egész kerületet szolgáltatja. A vizsgálatnak természetesen nem a kettővel való szorzás a fő problémája, hanem a szomszédok megkeresése a gráfban. |
Az irodalom [4] több szomszédság kereső algoritmust ismertet. Sajnos, didaktikai szempontból, mélyebb gráfelméleti ismeretek nélkül ezek egyike sem alkalmas a témával történő első ismerkedésre. A szerző alábbi algoritmusa talán nem a leggyorsabb, de szemléletessége, remélhetőleg, kezdők számára is érthetővé teszi ezt a komplex problémát.
Az algoritmus lineáris quadtree-s ábrázolást feltételez, de a 2.2.3.1 pont jelöléseit, a félreértések elkerülése végett, egy kissé megváltoztattuk a 2.43 ábrán látható módon: azaz az égtájak kódjait eggyel megnöveltük.
if szi[ni] MOD 2 = 0 then ki[ni,1] := szi[ni] - 1 else ki[ni,1] := szi[ni] + 1;
ki[ni,2]:= 5 - ki[ni,1]; {a keresővektorok utolsó, a fekete pixel hierarchiaszíntjén lévő tagjainak meghatározása}
repeat
e := ni;
for j:= 1 to 2 do
begin if ki[e,j] - szi[e] < 0 then ki[e-1,j] := 0 else ki[e-1,j] := 1
end; {ha a kereső vektor az előző hierarchia szinten 0, úgy onnét kezdve megegyezik szi-el, ha 1 értéket kap ez
csak azt jelenti, hogy nem 0 és a következőkben értéket kap}
if k[e-1,1] = 0 AND k[e-1,2] = 1 then
begin
if (szi[e]+szi[e-1]) MOD 2 = 0
then ki[e-1,2] := szi[e-1] - sz[e]
else ki[e-1,2] := szi[e-1] + szi[e]
end
else
begin
if ki[e-1,2] = 0 AND ki[e-1,2] = 1
then begin
if (szi[e]+szi[e-1]) MOD 2 = 0
then ki[e-1,1] := szi[e] +szi[e-1] - 2
else ki[e-1,1] := szi[e] + szi[e-1] -4
end
else begin
if (szi[e]+szi[e-1]]) MOD 2 = 0
then ki[e-1,1] := szi[e] +szi[e-1]
else ki[e-1,1] := szi[e-1] - szi[e];
ki[e-1,2] := 5 - ki[e-1,1]
end
end
A program a fentiek szerint felépíti a két kereső vektort az első 0 elemig. További, nem közölt, szegmensei pedig
ettől az elemtől kezdődően bemásolják a fekete pixel helyzetét leíró útvektor megfelelő elemeit a keresö vektorba.
Ezután sor kerülhet a szomszédok színének meghatározására. A keresés a gyökértől kezdődően indul és mindaddig tart,
amig a kérdéses út nem végződik levélben. Ez gyakorlatilag azt jelenti, hogy a ténylegesen használt kereső vektor
rövidebb is lehet a meghatározotnál. A 2.43 ábrán például a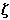 
fekete pixel útvektora
szz = 4 1 4 3, első keresővektora pedig k1 = 4 1 3 4, a szomszédos fehér tömböt (c) azonban a program már a
második hierarchia színten megtalálja a 4 1 3 út végén, ezért a kereső vektor utolsó eleme a keresésben már nem
játszik szerepet.
Természetesen az ilyen esetekben, amikor a szomszédos fehér tömb nagyobb mint a fekete tömb melyhez
szomszédot kerestünk, a kerület részösszegében a fekete tömb oldalhosszát kell figyelembe vennünk.
Fordított a helyzet akkor, ha a fekete tömb nagyobb mint a fehér szomszédja. Ilyen esetet mutat a 2.43 ábra m
fekete tömbje, melynek északi
szomszédai a 
fehér és a 
fekete tömb.
Ez a körülmény úgy jelentkezik a program számára, hogy a megtalált szomszéd szürke. Külön programágnak kell
foglalkozni ebben az esetben a keresővektor dimenziójának a szükséges mértékig (levélszíntig) történő növelésével.
Ebben az esetben a kerület szempontjából a kisebb fehér tömb oldal mérete a meghatározó.
Idomok területének a meghatározása
A közvetlenül mátrixban tárolt idomok (képek) területét egyszerű kettős ciklusban számolhatjuk, melynek ciklus magja mindíg eggyel megnöveli a számláló értékét, ha 1 attribútumú (fekete) pixelt talál.
Hasonlóan triviális a feladat megoldása sorkifejtő kódolás esetén is, be kell hívni a fekete pixeleket tartalmazó sorokat és összegezni a mezőkben tárolt koordináta különbségeket (feltételezve, hogy a területet pixel egységben keressük).
Lánckódolás esetén, bár a módszer nem írható le ilyen egyszerűen, a megoldásra számos hatékonykony algoritmus ismeretes.
A quadtree struktúra szinte felkínálja a megoldást: nem kell mást tenni csak hierarchia színtenként összegezni a fekete leveleket és számukat megszorozni a színtnek megfelelő tömbmérettel, majd a színtenkínti részterületeket összeadni.
Halmazműveletek (metszet, unió)
Mátrixban tárolt képek esetén a halmazműveletek is igen egyszerűen és szemléletesen hajthatók végre. Kettős ciklusba ágyazzuk a két képet leíró mátrixot és elemenként összehasonlítjuk őket. Metszet esetén az eredmény mátrix kérdéses eleme 1 lesz, ha mindkét összehasonlított mátrix elem értéke 1 (mind a kettő fekete) és 0, ha legalább az egyik összehasonlított elem értéke zérus. Unió esetén az eredmény akkor lesz 1, ha a két összehasonlítandó elem közül legalább az egyik fekete (1 értékű).
A halmazműveletek eredményesen hajthatók végre a quadtree struktúrában is. Metszet esetén, az algoritmus párhuzamosan járja be a két kép fáját és egyidejűleg létrehozza a metszet-fát is. Ha a két vizsgált csomópont bármelyike fehér, úgy az eredmény fa megfelelő csomópontja is fehér lesz. Ha például az első fán fekete csomópontot talál a program, úgy az eredmény csomópont színét olyanra változtatja, amilyen a második fa megfelelő csomópontja. Ha mindkét vizsgált csomópont szürke úgy a megfelelő csomópont a metszetben is szürke lesz és a vizsgálat, rekurzív módon, az első és második fán a szürke csomópontok leveleinek összehasonlításával folytatódnak. A két szürke csomópont leveleinek feldolgozása azt is eredményezheti, hogy a metszet fában mind a négy levél fehérre adódik, ezért ilyenkor még egy "beolvasztó" eljárást is alkalmazni kell, mely négy fehér levél esetén a metszet szürke csomópontját fehér levéllé alakítja, s négy korábbi fehér fiát törli.
Az unió művelet lefolyásában hasonlít a metszet végrehajtására. Az alapvető különbség abban van, hogy a fehér és fekete szerepe felcserélődik. Azaz, ha a két megfelelő csomópont egyike fekete, úgy az eredmény is fekete lesz. Ha az első fa vizsgált csomópontja fehér, úgy az eredmény csomópont színe meg fog egyezni a második fa megfelelő blokkjának színével. Ha mind az első, mind a második fában a megfelelő csomópont színe szürke, úgy az eredmény fa megfelelő csomópontja is szürke lesz, s a vizsgálat a két csomópont megfelelő fiainak vizsgálatával folytatódik. Összeolvasztásra az eredmény-fában akkor kerül sor, ha a szürke csomópont mind a négy fia fekete.
|
|
Remélhetőleg, a röviden felvázolt algoritmusok is megfelelően demonstrálják, hogy a raszteres adatmodell alkalmas a halmazműveletek végrehajtására. A GIS függvények bemutatásakor látni fogjuk, hogy hasonló feladatokat, a fedvényezési FIR művelet végrehajtásakor, csak igen körülményesen, jelentős gépidő ráfordítással lehet vektoros adatmodell felhasználásával megoldani.
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc
