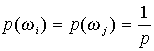Távérzékelés III

Ebben a részben a távérzékelési felvételek (jelenetek) hasznosításával fogunk foglalkozni. Ezen belül megismerkedünk

az osztályozás fogalmával ,
az ellenőrzött osztályozás alapgondolatával ,
a különböző szigorúságú osztályozási eljárásokkal megnézzük mit valósít meg az elméletből egy egyszerű oktatási GIS program, azaz megismerjük
az IDRISI képfeldolgozó moduljának főbb műveleteit és végül felvázoljuk
a mesterséges neurális hálózatok alkalmazhatóságát osztályozási feladatok megoldására.

A digitális űrtávérzékelés termékei a szenzor típusától függően többé vagy kevésbé eltérnek a fotogrammetriában megismert centrális vetülettől. Az eltérés lényegében két összetevőből ered: elektro-mechanikus szenzoroknál amikor is a képet csak egy vagy néhány szenzor alkotja lengő tükör segítségével (ilyenek a LANDSAT termékek) mindkét képkoordináta az idő függvénye is e mellett a lengőtükör geometriája u.n. panoráma hatással is torzítja a centrális vetületet. Bár e képek geometriai-matematikai modelljére megfelelő eljárások állnak rendelkezésre (lsd. pld [11]), a gyakorlatban a képeket rendszerint illesztőpontokra támaszkodva valamely polinómos transzformációval transzformálják a síkba.

A sordetektorok megjelenésével a centrális vetítés feltételeinek helyreállítása egyszerűbbé válik, habár itt is figyelembe kell venni az űreszköz esetleges pálya irányú tengely körüli elfordulását. Ha mátrix (keret) kamarával, vagy analóg kamarával készült és szkennelt felvételekkel dolgozunk, úgy a geometriai "korrekció" lényegében nem más mint a digitális fotogrammetriában már megismert ortofotó térkép létrehozása. Az ott elmondottakhoz azonban még egy kis módosítást kell eszközölnünk a magasságok vonatkozásában. Az ortofotó célokat szolgáló légifelvételek viszonylag kis területet fednek le, s ezért nem mindig igénylik, hogy a magasságokban figyelembe vegyük a föld görbület hatását is. A műholdas felvételekben azonban teljesen sík terep esetén is van 'magasságkülönbség' a vetületi sík és a leképezett földfelület között, ezért ennek figyelembe vétele az ortofotó készítéshez elengedhetetlen.

A jelen alpontban azonban nem kívánunk foglalkozni a geometriai kérdésekkel s csak utalunk a bemutatott modellre. Ugyanakkor pótolni szeretnénk azt a mulasztást, melyet azzal idéztünk elő, hogy a fotogrammetria felvázolásakor nem foglalkoztunk a fotóinterpretációval. Azaz míg a fotogrammetriával kapcsolatban alapvetően geometriai kérdésekkel foglalkoztunk, addig a távérzékelést döntően a tulajdonság jellemzők más szóval attributív adatok nyerése szempontjából fogjuk megvizsgálni. Tesszük ezt abból a meggondolásból, mivel a fotogrammetria geometriai modellje tiszta és áttekinthető, s a korszerű űrkamarák is egyre inkább ehhez a modellhez közelítenek, másrészt az attributív adatnyerésre az űrtávérzékelésben kidolgozott módszerek a repülőgépes felvételek elemzésénél is egyre inkább háttérbe szorítják a hagyományos interpretációs eljárásokat.

Ahhoz, hogy kitűzött célunkat elérjük meg kell ismerkednünk az osztályozás élvi kérdéseivel, majd néhány olyan osztályozási módszerrel, mellyel egy egyszerű raszteres GIS szoftver az IDRISI képfeldolgozó modulja operál.

Az osztályozás fogalma

Amikor a távérzékelés tulajdonság meghatározó képességéről beszélünk, különbséget kell tennünk három dolog között.

Az egyik lehetőség, amire a meteorológiai-geofizikai műholdak esetében már utaltunk, olyan számszerű információ kinyerése az érzékelt adatokból, melyek csak viszonylag lazán illetve kis felbontással köthetők a térbeli pozíciókhoz. Ilyen adatok pld. a földfelszín, felhők, tengerfelszín, jégtakaró hőmérséklete, az atmoszféra páratartalma, a szél iránya és sebessége stb.
A másik lehetőség, hogy valamely tulajdonság együttesek alapján a földfelszínt olyan foltokra bontsuk, melyekben ezek közösnek tekinthetők. Ezt a műveletet nevezzük osztályozásnak.
Végül ha az osztályozást sikerül elég finoman elvégezni s e mellett megfelelő természettudományos modelleket is képesek vagyunk felállítani, úgy az osztályozás és a modellek felhasználásával lehetőségünk van numerikus információt levezetni bizonyos jelenségre. Jó példa erre a várható gabona termés becslése, vagy olyan makroregionális kérdés vizsgálata mint a sivatagosodás, vagy az éghajlat globális változásának prognosztizálása.

Rövid áttekintésünkben csak az osztályozás azon kérdéseivel fogunk foglalkozni, melyek folt jellegű területi objektumokat eredményeznek. A vonalas objektumok felderítése és kiválasztása kapcsán elég utalnunk az élkiemeléssel kapcsolatban az előzőekben már ismertetett eljárásokra. Az egyéb szabályos alakú, általában mesterséges objektumok detektálására szolgáló alak felismerési módszerek ismertetése túlnő egy összefoglaló könyv keretein. Ez utóbbival kapcsolatban csak arra hívjuk fel a figyelmet, hogy a közeljövőben a nagyfelbontású digitális képi információ tömeges megjelenésével várhatóan e módszerek jelentősége rohamosan növekedni fog.

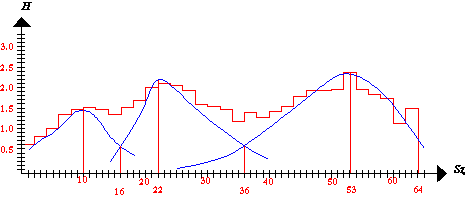
Az osztályozási eljárások alapgondolata abból a gyakorlati tapasztalatból indul ki, hogy a földfelszín különböző jellegű és borítású részletei más - más visszaverési tulajdonságokkal rendelkeznek, azaz a képeken más szürkeségi értékek tartoznak a különböző osztályokhoz. Ha a felvétel csak egy csatornán készül, úgy az osztályozást ennek a ténynek a felhasználásával az egydimenziós hisztogram partícionálásával, úgy nevezett küszöb értékek kijelölésével történik. Egy egy objektum típus akkor osztályozható viszonylag egyértelműen ha a hisztogramban az egyes osztályokhoz tartozó szürkeségi értékek olymódon válnak külön, hogy az egyes hisztogram részekre különböző paraméterű normális eloszlási sűrűségfüggvény illeszthető és e görbék összege jól közelíti az eredeti hisztogramot.

3.84 ábra - osztályozás egydimenziós hisztogrammal

A 3.84 ábrán egy ilyen szimulált hisztogramot mutatunk be.

Az ábrából jól látható, hogy a képen ábrázolt objektumokat leíró pixelek három szürkeségi érték tartományba csoportosíthatók. A tartományok közötti küszöbértékek a rész-hisztogramokat helyettesítő sűrűség függvények metszéseiből nyerhetők. Az egyes sűrűség függvények maximumaihoz tartozó abszcissza értékek az adott osztályra jellemző szürkeségi értéket szolgáltatják. Érdemes megfigyelni, hogy az egyes osztályokhoz tartozó sűrűség függvények nem egyenlő szélesek ami matematikailag úgy fogalmazható meg, hogy az egyes osztályokhoz tartozó szürkeségi értékek szórása általában különböző.

A vázolt módszer sok határozatlanságot rejt magában. A határozatlanságok részben csökkenthetők, ha a kép tartalmaz olyan területeket, melyekről előzetesen már biztosan tudjuk, hogy milyen osztályhoz tartoznak. Ebben az esetben elég megadni a kérdéses terület határoló görbéjét és a legtöbb képfeldolgozó program ezen az alapon extrapolálja az osztályozást, azaz minden olyan szürkeségi értékű pixelt a kérdéses osztályba sorol mely szürkeségi értékek találhatók az adott területen belül. A megoldás egyértelműsége azonban abban a pillanatban megszűnik, ha több ismert osztályt jelölünk ki és ugyanazok a szürkeségi értékek több osztályhoz tartozó ismert objektumban is megjelennek.

Az információ hiányt ezekben az esetekben különböző statisztikai módszerekkel próbálják pótolni, például a már vázolt sűrűség függvény helyettesítéssel. Ez annál inkább megtehető, mivel az ismert minták alapján a tapasztalati sűrűség függvények nagyobb megbízhatósággal interpolálhatóak. Ennél azonban szerencsésebb, ha több információból próbáljuk levezetni az osztályozást, bár a statisztikai módszerektől általában ebben az esetben sem tekinthetünk el.

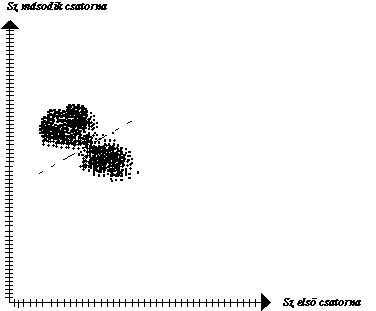
A távérzékelési műholdak azonban, amint azt az előző pontban láttuk, igyekeznek ugyanarról a területről különböző visszaverési tulajdonságokat feltáró felvételeket készíteni, gondoljunk a spektrális sávokra illetve a különböző hullámsávú és/vagy adó és vevő polaritású SAR felvételekre.

Ha kiszámítjuk két ugyanarról a területről, különböző spektrális csatornán készült felvétel kétdimenziós korrelációját az egydimenziós képlet alábbi síkbeli kiterjesztésével

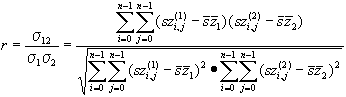ahol az 1 illetve 2 indexek a két csatornát jelölik, a felülvonás pedig továbbra is a számtani középértéket, úgy a korrelációs tényezőre az adott képen, különböző csatorna kombinációk esetén más és más értéket kapunk. Számunkra azok a kombinációk a legelőnyösebbek amelyek a legkisebb korrelációs együtthatót szolgáltatják.

Ha az osztályozást két vagy három csatorna alapján végezzük, úgy grafikusan is elkészíthetjük az objektumok két vagy háromdimenziós hisztogramját. A két vagy három dimenziós hisztogramban a derékszögű koordináta rendszer tengelyei az egy-egy csatornán tett észlelések szürkeségi értékeit reprezentálják. Minden pixelnek egy pont felel meg a két vagy háromdimenziós térben, melynek koordinátái megegyeznek a pixel szürkeségi értékeivel a kérdéses koordináta tengellyel reprezentált csatornán.

3.85 ábra - interaktív osztályozás kétdimenziós hisztogrammal

Az egyszerűség kedvéért szimulált adatokra készített kétdimenziós hisztogramot mutatunk be a 3.85-es ábrán. A hisztogramot eltérően az eddig megismert egydimenziós hisztogramtól nem 'oldalról' nézzük hanem 'felülről', ezért a gyakorisági értékeket nem tudjuk ordináták segítségével szemléltetni, e helyett a pontok gyakoriságára szürkeségi tónusokkal utalunk. Egyszerű kétdimenziós esetben az osztályozás interaktív módon a képernyőn az ábrán látható elválasztó vonal segítségével is elvégezhető.

Ahhoz azonban, hogy az osztályozás reális tartalommal is rendelkezzen az operátornak előzetes, latin szóval a priori ismeretekkel is kell rendelkeznie az osztályozás tárgyáról. Tudnia kell mindenek előtt, hogy az adott spektrális kombináció milyen felületi objektumra, szakszóval földhasználati osztályra jellemző, másrészt arról is tájékozottnak kell lennie, hogy az adott földhasználati osztály előfordulhat-e a vizsgált képen. Annak az ismérvnek alapján, hogy az előzetes információk tájékoztató jellegűek-e vagy az adott kép szempontjából szabatosak megkülönböztetik az ellenőrzés nélküli és az ellenőrzött osztályozás fogalmát, e kifejezések megfelelői az angol szaknyelvben supervised and unsupervised classification.

Az ellenőrzött osztályozás alapgondolata

Ellenőrzött osztályozás esetén más forrásokból (pld. GIS megfelelő fedvényéből) ismernünk kell a kép területén belül legalább egy-egy olyan terület körvonalának koordinátáit, mely biztosan a különválasztásra kijelölt földhasználati osztályt tartalmazza. Ezeket a területeket tréning vagy tanító területeknek hívják. A területek minden pixeléhez hozzárendelhető egy n dimenziós szürkeségi érték vektor (n az ugyanarra a pixelre eső (spektrális vagy SAR) csatornák száma):

Megjegyezzük, hogy nagy csatornaszám esetén úgy igyekeznek csökkenteni a feldolgozás számításigényét, hogy az azonos pixelekhez tartozó szürkeségi értékvektor elemekből kivonás, osztás, lineáris kombinációk segítségével komplex vektorelemeket képeznek s így csökkentik a vektor dimenzióját. A továbbiak szempontjából azonban a dimenzió csökkentésen kívül nincs elvi jelentősége annak hogy sz elemei eredeti mérésből vagy azok kombinációiból származnak. Néhány dimenzió redukciós módszer leírást [11]-ben és [12]-ben talál az érdeklődő.

Jelöljük a megkülönböztetendő m számú osztályt az alábbi formális vektorral:

Rendelkezésünkre áll tehát mind az m osztályban annyi sz szürkeségi érték vektor ahány pixel a kérdéses osztályhoz tartozó tanuló területen volt. Ezekre a pixelekre osztályonként elkészíthető az n dimenziós hisztogram, amely azonban számunkra grafikusan csak n=1 és n=2 esetén ábrázolható. Ha a szemléltetés véget n=2-t választunk, úgy a hisztogramot alkotó felület többé kevésbé hasonló lesz a 3.48 ábrán bemutatott körszimmetrikus kétdimenziós normális eloszlás sűrűségfüggvényéhez. Alá kell húznunk, hogy az alak oldaláról csak több vagy kevesebb hasonlóságról van szó, az igazi hasonlóság a két felület, a hisztogram és a sűrűség függvény tulajdonságaiban van, ugyanis a hisztogramból sűrűségfüggvény válik, ha a pixelek mérete a zérushoz s következésképpen a szürkeségérték vektorok száma pedig a végtelenhez tart, s e mellett a szürkeségi értékeket ábrázoló koordináta tengelyeken a két beosztás közötti távolság egységnyi. Röviden tehát azt mondhatjuk, hogy a tanuló terület hisztogramja közelíti a szürkeségi érték vektorok adott osztályra jellemző sűrűségfüggvényét, melyet a továbbiakban -el jelölünk (a p jelölés, mellyel rendszerint a valószínűséget jelöljük alkalmazása nem véletlen, mivel a sűrűség függvény értéke annak a valószínűségét adja meg, amellyel az adott szürkeségi érték vektor a kérdéses mintában helyet foglal).

A hisztogram tehát empirikus sűrűség függvénynek is tekinthető, azonban mivel nem analitikus függvény a vele végrehajtott műveletek kiterjedt, többdimenziós táblázatokban való keresést igényelnek, e mellett az alábbi Parzen-Rozenblatt eljárás (lsd. [12]) nagyobb pontosságot nyújt a valószínűségek meghatározásában.

Első lépésben keresnünk kell egy olyan 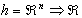(vektor argumentumú skalár) szimmetrikus sűrűség függvényt, mely kétszer korlátosan differenciálható és melyre teljesülnek az alábbi feltételek:

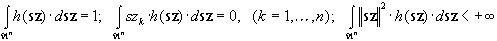ekkor az osztály közelítő sűrűség függvényét a következő alakban írhatjuk fel:

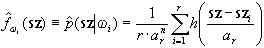ahol r az összes pixel (szürkeségi érték vektor) száma, a_r pedig egynél nagyobb állandó. Mind az a_r állandót, mind pedig a választott h szimmetrikus sűrűségfüggvény paramétereit az egyéb eloszlásokkal kapcsolatban alább kifejtendő módon az n dimenziós hisztogram felhasználásával számítjuk.

További közelítés, ha a hisztogramot valamely ismert eloszlás sűrűségfüggvényével kívánjuk helyettesíteni.

A különböző eloszlás típusokat meghatározó függvények (lásd bővebben az [5] 18. fejezetében vagy a [16]-ban) szabad paramétereit a tanuló terület hisztogramjának segítségével legkisebb négyzetes becsléssel határozhatjuk meg. Ha ugyanarra a hisztogramra különböző eloszlások sűrűségfüggvényeit próbáljuk illeszteni, úgy azt fogjuk tapasztalni, hogy a különböző függvénytípusok illesztési pontossága különböző lesz ( tekintsük a pontosság mérőszámának valamennyi szürkeségi vektorhoz tartozó hisztogram érték és interpolált sűrűségfüggvény érték különbségének négyzetösszegét). Kézenfekvő, hogy a valóságot annak az eloszlásnak a sűrűségfüggvénye közelíti meg a legjobban, melynek az előzőekben definiált eltérési négyzetösszege a minimális. Ez a vizsgálat azonban nagyon sok gépidőt vehet igénybe ezért gyakran eltekintenek tőle és feltételezik, hogy az egy osztályon belüli szürkeségi érték vektorok normális eloszlásúak. Ezt a feltételezést egyrészt a gyakorlati tapasztalatok alapján teszik, másrészt azért mert a normális eloszlás matematikailag viszonylag egyszerűen kezelhető. Az n dimenziós normális eloszlás sűrűségfüggvénye az alábbi formában írható fel:

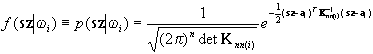ahol a már ismert jelöléseken túl a következők szorulnak magyarázatra:

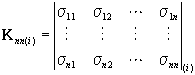
az osztályhoz tartozó szürkeségi értékek variancia-kovariancia mátrixa,

pedig a szürkeségi értékek csatornánkénti középértékeinek vektora az osztályban.

Az eloszlás sűrűségfüggvénye akkor lesz meghatározott, ha kiszámítjuk szabad paramétereit: a variancia-kovariancia mátrix elemeit valamint a csatornánkénti átlagos szürkeségi értéket. Ezek empirikus értékeit az alábbi kifejezésekből nyerjük:

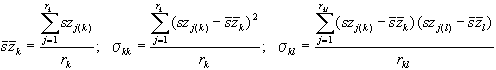Meg kell még magyaráznunk néhány jelölést: r_k a k-adik csatorna által leképezett pixelek száma, r_klpedig a k-adik illetve az l-edik csatorna által leképezett pixel elemek száma közül a nagyobb. A gyakorlatban azonban nincsen jelentősége a csatornánként különböző számú pixel felvételének, ezért nem követünk el nagy hibát ha r-et index nélkül használjuk.

Az empirikus értékek mint közelítő értékek birtokában a legkisebb négyzetes kiegyenlítéssel a meglévő hisztogram értékekre illesztjük a függvényt olymódon, hogy kis mértékben megváltoztatjuk a paraméterek közelítő értékeit és evvel elérjük, hogy a függvény és hisztogram eltéréseinek négyzetösszege minimális legyen.

Ezután rátérhetünk az osztályozás alapelvének az ismertetésére. Ehhez azonban először meg kell ismerkednünk az alábbi formában is megadható Bayes-féle becsléssel:

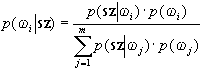A képlet baloldalán annak az a posteriori (utólagos) valószínűsége szerepel, hogy az sz szürkeségi értékvektorral rendelkező pixel az osztály tagja, a jobboldal számlálóját az osztály sűrűségfüggvénye alkotja, megszorozva annak az a priori (előzetes) valószínűségével, hogy az osztály egyáltalán létezik a képen. A nevező ugyanazt az értéket, amit a számláló az osztályra képez összegzi valamennyi osztályra.

A képletben szereplő tagok közül már részletesen megismerkedtünk a sűrűségfüggvénnyel de még nem szóltunk az a priori valószínűségről. Ezt az értéket tapasztaltból, a képtartalom vizuális-logikai elemzéséből tudjuk becsülni. Ilyen alapokon természetesen pontos számokról nem lehet szó, de az fölöttébb kívánatos, hogy az egyes osztályok egymáshoz viszonyított valószínűsége jól tükrözze a valóságot.

Az a posteriori valószínűség birtokában felírhatjuk az osztályozás alaptörvényét:

Szóban kifejtve a szabály, melyet azért mivel az osztályokhoz tartozás eldöntésére szolgál diszkrimináns függvénynek is hívunk, azt mondja ki, hogy az sz vektor akkor tartozik az osztályhoz, ha arra vonatkoztatott a posteriori valószínűsége nagyobb bármely más konkurens osztályra vonatkoztatott valószínűségénél.

Különböző szigorúságú osztályozási eljárások

További vizsgálatainkban a szürkeségi érték vektorok normális eloszlását feltételezzük.

Helyettesítsük be az n dimenziós normális eloszlás sűrűség függvényét a diszkrimináns függvénybe, logaritmáljuk és egyszerűsítsük a kifejezést, e műveletek eredményeképpen gyakorlati eszközt nyerünk az osztályba sorolási döntés meghozásához.

Ezek szerint általános esetben, amikor minden osztály variancia-kovariancia mátrixa, illetve a szürkeségi értékek középértékeiből képzett vektora különböző, az osztályba akkor soroljuk az sz szürkeségi érték vektorral jellemzett pixelt, ha az átalakított

diszkrimináns függvény k=i-re maximális.

Előföldolgozások céljaira gyakran tovább egyszerűsítik az eloszlásokra vonatkozó hipotéziseket.

A második egyszerűsítés (ne feledjük, az első egyszerűsítés az volt, hogy normális eloszlást tételeztünk fel) abban áll, hogy minden osztályhoz azonos variancia-kovariancia mátrixot rendelünk, azaz ebben az esetben, melyet Mahalanobis osztályozásnak nevezünk, a diszkrimináns függvény tovább egyszerűsödik az alábbiak szerint:

Az sz szürkeségi érték vektorral rendelkező pixelt itt is abba az osztályba sorolják amely k=i esetén maximalizálja a diszkrimináns függvényt.

További egyszerűsítéssel él a legközelebbi szomszédság módszere. A módszer ugyanis feltételezi, hogy , ahol E_nn az n dimenziójú egységmátrix (olyan nxn-es mátrix, melynek az átlójában egyesek a többi helyein nullák vannak), pedig valamennyi osztály közös szórása.

Erre a speciális esetre a diszkrimináns függvényt az alábbi egyszerű alakban írhatjuk fel:

Az osztályba sorolás kritériuma továbbra sem változott: az sz szürkeségi érték vektorú pixel abba az osztályba kerül, melyre a diszkrimináns függvény maximális értéket ad.

Ha az osztályba sorolást az osztályozás alaptörvénye alapján kívánjuk végezni, de semmi információnk sincs az osztályok előzetes valószínűségéről, úgy logikus

hogy erre a paraméterre egyenletes eloszlást tételezzünk fel, ami azt jelenti, hogy

következésképpen az egyenlőtlenség bal és jobb

oldalát egyszerűsíthetjük az osztály a priori valószínűségével s így az osztályba sorolás kritériuma kizárólag a szürkeségi érték vektor osztályon belüli megjelenésének valószínűsége marad. Ezt az eljárást maximumum likelihood (legnagyobb valószínűség) módszernek nevezik.

A legnagyobb valószínűség módszere tehát független attól, hogy az eloszlásban milyen egyszerűsítő feltételezéseket alkalmazunk, s ezért az egyszerűsített diszkrimináns függvény kifejezések e módszerben is alkalmazhatók azzal a módosítással, hogy a jobb oldali első tagot egyszerűen elhagyjuk.

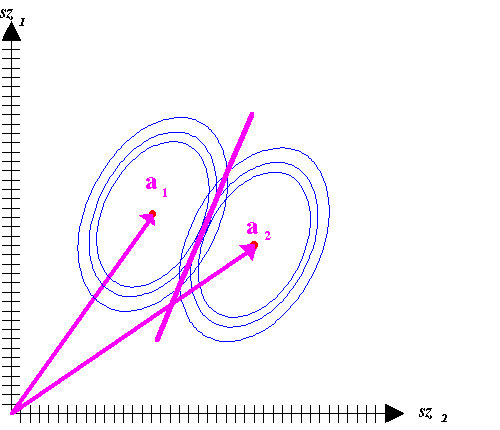
Ebben az esetben különben a három közelítés (normális eloszlás de külön variancia-kovariancia mátrix minden osztályra, normális eloszlás de közös variancia-kovariancia mátrix, normális eloszlás de közös átlós (diagonális) variancia-kovariancia mátrix) két dimenziós esetre grafikusan is viszonylag egyszerűen szemléltethetők.

3.86 ábra - kétdimenziós maximumum likelihood osztályozás első közelítéssel

A 3.86 ábrán két normális eloszlású osztály azonos eloszlás értékekhez tartozó isovonalait rajzoltuk meg. Az isovonalak a két osztály esetén különböző méretű és tájolású ellipszisek. Kézenfekvő, hogy az osztályok közötti válaszvonalat a két osztály azonos valószínűséget ábrázoló isovonalai metszéspontjait összekötő görbe fogja szolgáltatni.

A 3.87 ábrán a Mahalanobis osztályozást illusztráltuk. Ebben az esetben az azonos valószínüségű vonalak egybevágó, azonos tájolású ellipszisek. A két osztály azonos valószínűségű vonalainak metszéspontjai egy egyenesen helyezkednek el.

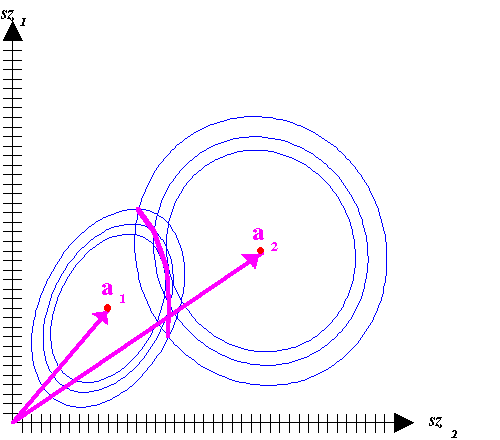
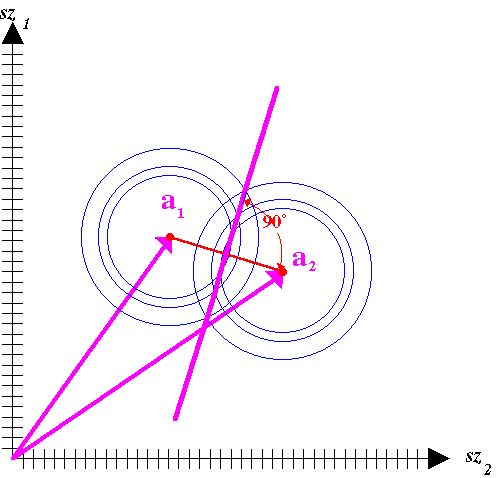
3.87 ábra - kétdimenziós maximumum likelihood osztályozás második (Mahalanobis) közelítéssel

3.88 ábra - kétdimenziós maximumum likelihood osztályozás harmadik közelítéssel

A legközelebbi szomszédság alapján történő osztályozás esetén, amint ezt a 3.88 ábrán látjuk, az azonos valószínűségű vonalak a két osztály esetén azonos sugarú körök, s ezek metszéspontjait összekötő egyenes merőleges a két osztályközéppontot (az osztály szürkeségi érték vektorainak számtani közepére illeszkedő pont, eddigi jelölésünkkel a_i) összekötő egyenesre.

Az IDRISI képfeldolgozó moduljának főbb műveletei

Az alpont célja, hogy bemutassa hogy miként realizálódnak az elméleti megfontolások egy gyakorlati programban. Amint azt valószínűleg az olvasó is érzékelni fogja, még egy oktatási célú programban sem teljesen világos a megfeleltetés az elméleti törvények és program utasítások között. Még kevésbé él ez a kapcsolat a termelési célú programokban.

Az IDRISI utasításokat hozzákapcsoltam az IDRISI Oktató anyaghoz, az érdeklődők ott tovább tanulmányozhatják a témát (feltéve, hogy a kérdéses fejezet az oktató anyagban már elkészült).

A képfeldolgozó modul három fő részből áll.
Az első rész neve 'képhelyreállítás' (image restoration), mely műveletcsoportjai a következők:
SCALAR egy olyan egyszerű szűrést valósít meg, mely eltávolítja a párásságot a képről. Alapelve az, hogy megvizsgálja a vízfelületek szürkeségi értékeit a felvétel összes sávjában. Ha ezek lényegesen meghaladják zérust, úgy ezt az értéket kivonja valamennyi pixel értékéből. Tulajdonképpen a módszer egy korábban bemutatott transzformáció olyan speciális esete, ahol az f függvény konstans.

RADIANCE az egy előző részben ismertetett radiometrikus korrekcióval javítja a képet. Ehhez arra van szükség, hogy rendelkezésre álljanak az adott időpontra szóló kalibrációs táblázatok.

RESAMPLE szolgál geometriai javításokra. Fő funkciója a 'gumilepedő transzformáció' illetve egyéb (pld. a földgörbület hatását kiküszöbölő) korrekciók végrehajtása.

A második főrész a képkiemelés (image enhancement) a következő műveletcsoportokat tartalmazza:
FILTER a lineáris szűrési eljárásokat valósítja meg, adott 3x3-as szűrőmátrix segítségével.

DESTRIPE csökkenti a 'csíkozást' amit a különböző szenzorok eltérő működése idéz elő. A program működéséhez nem kell korrekciós táblázat, mivel a szűrést azon az alapon végzi, hogy kiszámítja az egész kép valamint az egyes szenzorok által előállított képrészlet szórását és középértékét, majd úgy módosítja a részképeket, hogy azok szórása és középértéke megfeleljen az egész képre számított értékeknek.

A STRETCH segítségével lehetőség nyílik a hisztogram nyújtási és kiegyenlítési eljárások végrehajtására.

PCA szabványos és nem szabványos főkomponens analízis végrehajtására szolgál. Ezekkel a kérdésekkel nem foglalkoztunk, a részletek iránt érdeklődőknek a [10], [11] és [12] megfelelő fejezeteit ajánljuk. Érdemes megemlíteni, hogy ez a program alkalmas arra is, hogy segítségével az eredetileg engedélyezett 3 sávnál több sávból lehessen úgy nevezett színes kompozitokat létrehozni.

A harmadik főrész a képosztályozás (image classification). Az IDRISI lehetőséget biztosít mind az ellenőrzött mind az ellenőrzetlen osztályozásra.

Ellenőrzött osztályozás esetén az első lépésben a tanuló területek digitalizálását végzik el a COLOR d opciójával. A második lépés a kijelölt területek alapján a minta szürkeségi érték fájlok létrehozása a MAKESIG programmal. Ezek az értékek módosíthatók az EDITSIG programmal, illetve összehasonlíthatók grafikusan a SIGCOMP program segítségével. Ez utóbbira azért van szükség, mivel a sávonkénti jellemzők összehasonlító vizsgálata támpontot nyújt arra, hogy melyik osztályozási rutint célszerű választanunk. Három osztályozási eljárás közül választhatunk. Ezek gyorsasági, tehát megbízhatósági szempontból fordított sorrendben a következők:

PIPED n dimenziós téglatesteket képez minden minta terület minden sávja minimális és maximális szürkeségi értékeiből, és a vizsgált pixel akkor van benne a minta által reprezentált osztályban, ha szürkeségi érték vektora a téglatesten belül van. Mivel ez az osztályozás nem egyértelmű, a több osztály kritériumait is kielégítő pixeleket mindig abba az osztályba sorolja a program amely mintájához utoljára sorolta.

· MINDIST néven fut az a rutin, mely a legegyszerűbb diszkrimináns függvény előzetes osztály-valószínűség nélküli variánsa és két dimenziós esetre a 3.88 ábrán került bemutatásra.

· MAXLIKE néven szerepel a szoftver legpontosabb rutinja, mely képes az osztályokra vonatkozó előzetes valószínűségek figyelembe vételére is, azaz tulajdonképpen nem is igazán a maximum likelihood módszert hanem a tágabban értelmezett Bayes-féle osztályozási törvényt realizálja normális eloszlás esetére.

· Az ellenőrzés nélküli osztályozás lehetőségeire egydimenziós esetben a 3.84, kétdimenziós esetben pedig a 3.85 ábra kapcsán utaltunk. Az IDRISI háromdimenziós képeken képes végrehajtani az úgy nevezett cluster analízist, azaz magyarul a sűrűsödésekből előálló alakzatok - osztályok létrehozását. Mindehhez először a COMPOSIT programmal létre kell hozni három spektrális csatornából a színes kompozit képet, mely tulajdonképpen három csatornán létrejött 6 színtű kép 216 színre történő leképezése. A leképezett pixel indexét megkapjuk, ha az első csatorna 0-tól 5-ig terjedő szürkeségi értékéhez hozzáadjuk a második csatorna értékének (szintén 0-tól 5-ig terjed) hatszorosát valamint a harmadik csatorna értékének (ez is 0-tól 5-ig terjed) a 36 szorosát.

CLUSTER nevű program végzi a kompozit képen az osztályozást. Az osztályozás lényege, hogy a program visszaalakítja az egyesített képet elemi csatornáira, létrehozza a háromdimenziós hisztogramot, majd az osztályokat a hisztogram csúcsai köré alakítja olymódon, hogy az osztály közepe a csúcs, a hozzátartozó osztály pedig a szomszédos csúcsok közötti távolság felezőéig tart.

Távérzékelési jelenetek, GIS objektumok osztályozása neurális hálózatok segítségével

A korábbiakban már megismerkedtünk a mesterséges neurális hálózatok fogalmával, az MLP hálózat architektúrájával, a hálózat tanítását szolgáló "visszaterjedés" (backpropagation) algoritmussal és a hálózat felhasználásával térbeli interpolálásra.

Ugyanezek a hálózatok azonban használhatók osztályozásra is, ha annyi kimeneti csomópontot alkalmazunk ahány osztályunk van, és a csomópontok sorszámát megfeleltetjük az az osztályok nevének (pld. a 6. kimenetet a tűlevelű erdőnek).
Mivel azt tudjuk, hogy a tréning adatok egy összetartozó spektrális intenzitás együttese (tréning paraméter vektora) milyen osztályhoz tartozik, megkívánt kimeneti értéként egyest rendelünk ahhoz a kimenethez, amely sorszáma megfelel a kérdéses osztály sorszámának és nullást az összes többi kimenethez. Ezután a tréninget ugyanúgy futtatjuk, mint az interpoláló hálózat esetén. A tanított hálózat ezek után úgy végzi az osztályozást, hogy azon a kimeneten ad egyest amely sorszáma megfelel a meghatározandó minta paramétervektorát tartalmazó osztály sorszámának.
Az MLP hálózatok mellett azonban más hálózat típusokat is alkalmazhatunk pld. az egy rejtett réteggel rendelkező a radiális bázis függvény (RBF) hálózatokat, a kimeneti csomópontok száma ebben az esetben is megegyezik a kialakított osztályok számával.
Teljesen más elveken működik a Tanuló Vektor Kvantálás (LVQ) módszert realizáló hálózattípus (3.88a ábra).

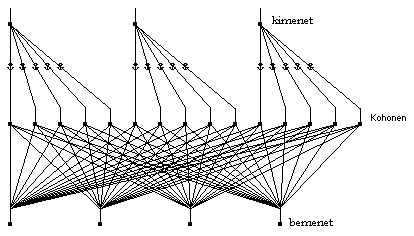
3.88a ábra - LVQ típusú osztályozó hálózat

A hálózat három rétegből áll: a normalizált paraméterek bevitelére szolgáló bemenő rétegből, az úgy nevezett Kohonen rétegből és az osztályokat képviselő kimenő rétegből.
A bemenő rétegnek csak akkor van külön funkciója, ha a paraméter vektorok nem egyforma és egységnyi hosszúak, ebben az esetben ugyanis ennek a rétegnek kell elvégezni az egységre normálás feladatát is.
Külön érdeklődésre tarthat számot az u.n Kohonen réteg. A réteg nevét feltalálójáról Teuvo Kohonen finn professzorról nyerte. Kohonen 1982-ben dolgozta ki ezt a rétegtípust felügyelet nélküli klaszterező módszere számára (Self Organizing Maps=SOM), majd a 80-as évek végén ugyanerre a rétegtípusra támaszkodva alkotta meg az LVQ algoritmusokat. (Mind a SOM mind az LVQ programcsomag az internetről szabadon letölthető).
A kimeneti réteg egyszerű összegző funkciót lát el.

Részben, hogy a Kohonen réteget jobban megismerjük, részben hogy megismerjünk egy felügyelet nélküli eljárást és végül, hogy előkészítsük az LVQ algoritmust foglaljuk össze röviden a SOM eljárást.
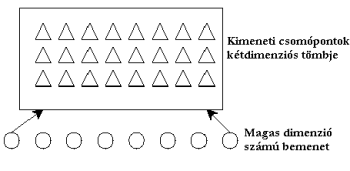
A SOM eljárás lényege hogy az n dimenziós bemenő adatokat szabályos kétdimenziós tömbökre képezi le, és a leképezés eredményét grafikusan és numerikusan ábrázolja.
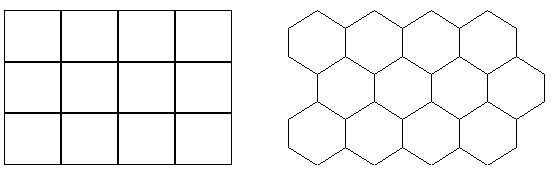
A 3.88b. ábrán azt a két terület felosztási variációt látjuk, amelyet a korszerű SOM szoftverek (például a NENET nevű win95 alatt működő) használnak.

3.88b ábra - SOM tesszellációs minták

Minden egyes cellához tartozik egy referencia vektor, mely analóg az MLP hálózatoknál megismert súlyokkal. Mivel ezek a súlyok összekapcsolják a kérdéses cellát az összes bemenettel ezért az egyes összeköttetések úgy tekinthetők, mint a kérdéses cella súlyvektorának komponensei. Kézenfekvő tehát, hogy a súlyvektor dimenziója megegyezik a bemenő paraméter vektor dimenziójával.
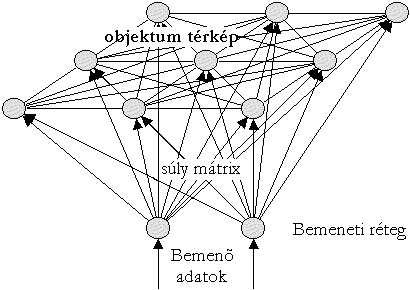
A 3.88c ábra a kimenő csomópontok kétdimenziós tömbjét állítja szembe a többdimenziós bemenő vektorral. Hogy a konstrukció még érthetőbb jegyen a 3.88d ábrán bemutattuk magukat az összeköttetéseket is, igaz hogy csak kétdimenziós bemenő adatok esetére.


3.88c ábra - SOM leképezés	3.88d ábra - SOM leképezés két dimenziós bemenő vektorból

Minden bemenő vektorhoz keresünk egy olyan súlyvektort, mely legközelebb van hozzá, azaz melytől számított (euklideszi) távolsága a legkisebb. Képlettel kifejezve:

ahol c jelenti az x vektort leképező cella indexét.
A tanítási folyamat során mindazok a cellák aktiválódnak a kérdéses x vektortól, melyek bizonyos távolságon belül helyezkednek el a kiválasztott c cellától. A hasznos w_i súlyokat a kezdetben tetszőlegesen megválasztott w_i(0) értékekből kiindulva a következő tanítási folyamat konvergencia határaként nyerjük:

ahol h_ci a szomszédsági függvény. A c cella figyelembe vett szomszédságát (cella számát) N_c(t)-vel jelöljük, ami azt is jelenti, hogy ez a sugár nem állandó, hanem a tanulási folyamat során változik ( t növekedésével csökken). Ha az i indexű cella benne van az N_c(t)-vel jellemzett cellatartományban úgy , ahol és a függvény monoton csökken.

A tanítás befejezése után a "térkép" a 3.888e ábrán bemutatott képre lesz hasonló. Ahhoz hogy a tanult hálózatot vizuális interpretálásra fel tudjuk használni manuálisan ki kell választanunk olyan adatokat melyeket a kérdéses feladat kapcsán ismerünk és segítségükkel a tanult térképet fel kell címkéznünk. Ezután a teljesen ismeretlen adatok bevitele után interpolációval illetve extrapolációval értékelni tudjuk azok kapcsolatát a címkézett klaszterekkel.

Hogy egy példát is lássunk, a már hivatkozott NENET program mintapéldája egy technológiai együttesen végrehajtott 5 mérőhely 3480 mérését használta a hálózat tanítására.
A tanítás eredményeképpen létrejönnek a cellákhoz rendelt végleges súlyvektorok, melyek egy .map végződésű fájlban kerülnek tárolásra. Ugyanakkor a rendszer kiszámítja az úgy nevezett U mátrixot, mely elemei tartalmazzák a cellákhoz tartozó súlyvektorok egységre normált, átlagos távolságát a 6 (négyzet raszter esetén 4) szomszédos súlyvektortól. Az élek színezése a kérdéses él mentén fekvő szomszéd cella súlyától mért távolságot reprezentálja.
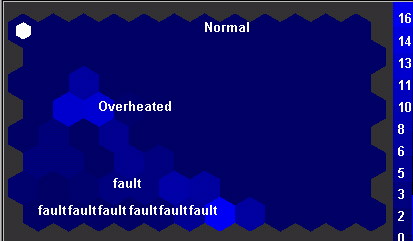
A példánkra érvényes súlytávolság térkép a 3.88e ábrán látható. Kis gondolkodás után rájöhetünk arra, hogy tulajdonképpen a korábban már megismert Voronoi cellák egy speciális ábrázolási formájával állunk szemben.

3.88e ábra - SOM térkép

Arról van tehát szó, hogy az algoritmus egy felvett maximális topológiához hozzárendelte a bemenő adatokat legjobban leképező Voronoi cellákat, azaz azokat a súlyvektorokat, melyekhöz egy-egy csoport bemenő vektor közelebb van mint bármely más súlyvektorhoz.

Ha ugyanis a szomszédos cellák középpontját eltolnánk egymástól az élekben kódolt távolságokra és meghúznánk a középpontokat összekötő oldalak felező merőlegeseit, akkor azok kimetszenék a klasszikus Voronoi cellákat.

3.88f ábra - cimkézett SOM hisztogram

A következő tesztelési fázisban manuális elemzéssel kiválogattak 96 vektort, mely mérésekor a rendszer normálisan üzemelt, 246 hibás működéskor felvett rekordot és 96 olyan rekordot mely mérésekor a rendszer túlmelegedett.
A 3.88f ábrán azt láthatjuk, hogy hol helyezkednek el és milyen gyakorisággal a normális, hibás és túlmelegedett üzemnek megfelelő vektorok.

Amint látható, a túlhevített állapot a normális és a hibás működés között helyezkedik el, és interpretálható, hogy átmenetet képez a meghibásodás felé.

Számunkra azonban a SOM azért volt érdekes, mivel elvileg is (a Kohonen réteg bemutatásával) és gyakorlatig is (a kezdeti súlyok kialakításával) átvezet minket Kohonen ellenőrzött osztályozási eljárása a Tanuló Vektor Kvantálás (Learning Vector Quantization = LVQ) tárgyalásába.

A 3.88a ábrán vázoltuk fel az LVQ osztályozásnál használt hálózatot.
A Kohonen réteg azonos számú cellája reprezentál egy-egy osztályt. Minél több cella tartozik egy osztályhoz annál finomabb az osztályozás. A cella szám növelésének azonban határt szabnak a számítási erőforrások.
Az inicializálási lépésben minden cellához hozzá kell rendelni egy reprezentatív w_i súlyvektort az úgy nevezett kódkönyv vektort. Ezeknek a vektoroknak a végleges értékét határozzuk meg a tanítási folyamatban.

A végleges súlyvektorok ismeretében bármely ismeretlen bemeneti vektort ahoz az osztályhoz rendel az algoritmus amelyhez tartozó valamelyik súlyvektortól számított távolsága minimális.
A súlyok inicializálását elvégezhetjük az előzőekben ismertetett SOM algoritmussal, vagy egyszerűen, biztosan osztályozott bemenő vektorokkal. Hogy ezek a vektorok biztosan mentesek legyenek az osztályozási hibáktól, célszerű előzetesen valamilyen hagyományos osztályozási eljárással (Kohonen javaslata szerint a legközelebbi szomszédság módszerével) minden kiválasztott vektort a többi tanító vektorhoz képest újra osztályozni.

A tanítási folyamatra több alternatív illetve szekvenciálisan alkalmazható algoritmust is kidolgoztak. Az LVQ1 algoritmus a tanítási folyamatot a következő kifejezésekkel irja le. Jelöljük a kérdéses bemeneti paraméter vektort a t.-ik tanulási ciklusban x(t)-vel, a hozzá legközelebbi súlyvektort (kódkönyv-vektort) w_c(t)-vel, a monoton csökkenő tanulási sebesség függvényt -vel, ahol . A tanulási (súlymódosítási) szabály

ha x és w_c ugyanahhoz az osztályhoz tartozik

ha x és w_c különböző osztályhoz tartozik

az összes többi, nem legközelebbi súlyvektor a ciklusban változatlan marad, azaz

Az LVQ2.1 algoritmus abban különbözik az LVQ1-től, hogy két, legközelebbi súlyvektort módosít egyidejűleg, mégpedig a w_j-t, mely az x-el azonos osztályú legközelebbi súly és a w_i-t, mely az x-hez legközelebbi különböző osztályú súly. A módosításhoz még az is szükséges, hogy az x "beleessen" az a szélességű ablakba. Ha az x távolságát a w_j-től d_j-vel, a w_i-től pedig d_i-vel jelöljük akkor a beleesés feltétele, hogy

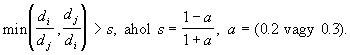
A módosított súlyok a következő képletekből számolhatók:

Az LVQ3 algoritmus továbbra is az előbbi képleteket használja a javításra, ha a két legközelebbi súlyvektor közül az egyik az x osztályához tartozik a másik nem és az x beleesik az ablakba. Arra az esetre vonatkozóan azonban ha mind a két közeli súlyvektor x osztályához tartozik és x belesik az ablakba az LVQ2.1 algoritmus nem rendelkezett, értelemszerűen ebben az esetben csak az egyik, a legközelebbi súlyvektor változtatására került sor. Mivel ez az eset a tanítási folyamat fejlődésével gyakran előfordul az LVQ3 gondoskodik arról, hogy mindkét közeli súly változtatására sor kerüljön. Abban az esetben tehát, ha mind az x, mind a w_i, mind a w_j azonos osztályba tartozik

Az értékére a kísérleti futtatások alapján 0.1 és 0.5 értékeket javasolnak az algoritmus kidolgozói.