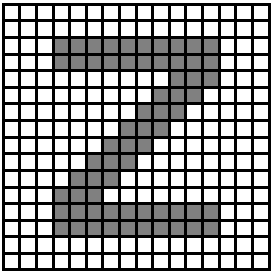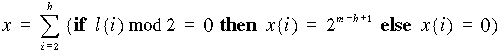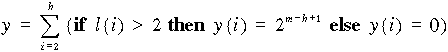Grafikus adatmodellek III

Ebben a részben megismerkedünk:

  1. a raszteres-teszellációs modellek általános kérdéseivel,
  2. a raszteres adatmodellel, és
  3. az alábbi rasztertömörítő eljárásokkal:
    1. a "sorkifejtő kódolás vagy run-length encoding",
    2. a "lánckódolás vagy chain encoding",
    3. a "középtengely transzformáció vagy medial axis transformation",
    4. a "négyes fa vagy quadtree" és ez utóbbi további tömörítést lehetővé tevő alábbi változatai:
      1. a lineáris négyágú fák (linear quadtrees),
      2. a négyágú fa normalizálás (quadtree normalization),
      3. a négyágú fa középtengely transzformáció (quadtree medial axis transformation),
      4. a négyágú fa erdők (quadtree forests) és
      5. a négyágú fa hálók (quadtree meshes).

Raszteres-teszellációs modellek

A vektoros ábrázolás a hagyományos ceruza-, vagy tusrajzból ered, hisz a toll is elemi egyenes darabok összegeként húzza meg azokat a vonalakat, melyek a térbeli objektumokat alkotják illetve határolják. A teszellációs modellek lényegében a fényképek és a számítógép monitorok ábrázolásmódját választották mintaként a grafikus adatok modellezéséhez.

A módszer lényege, hogy a kérdéses felületet felosztja elemi területekre olymódon, hogy azok folyamatosak és kihagyásmentesek legyenek. Az objektumok képét a benne foglalt elemi területek befeketítésével (színezésével) oldja meg a modell.
2.8 ábra - z betű ábrázolása raszterben

 

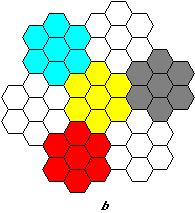
Az elemi felületek a legtöbb alkalmazásban szabályos idomok, négyzetek és háromszögek, de esetenként hatszögek is játszhatják ezt a szerepet. A teszelláció hierarchikus modellekbe szervezhető (2.9 ábra).

 
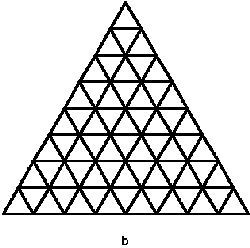
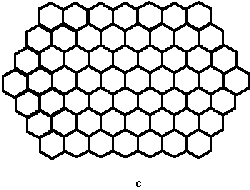
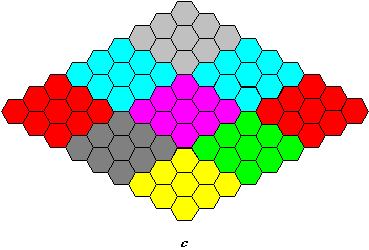
2.9 ábra - (a) négyzet, (b) háromszög, (c) hatszög alapú tesszelláció

 

A legáltalánosabb esetben a képbontási módszer két alapvető tulajdonsággal kell, hogy rendelkezzen:

  1. A partíció (alapelem) tetszés szerint ismételhető kell, hogy legyen azért, hogy segítségével bármilyen méretű képet le lehessen írni;
  2. A felbontás tetszés szerinti finomítása az alapelem korlátlan tovább bonthatóságát igényli.

Szabályos teszellációról akkor beszélünk, ha az elemi (atomi) felületek szabályosak: oldalaik és szögeik egyenlőek. Az elemi felületekből (atomokból) nagyobb egységek (molekulák) szervezhetők, ezek azonban nem feltétlenül konformak a felületelemekkel. Amennyiben a konformitás fennáll, a felosztást hasonlónak nevezzük.

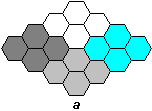
A 2.9 ábra szabályos felosztási változatai közül csak az a és b elégíti ki a 2. feltételt (t.i. hogy tetszés szerinti mélységig tovább osztható). Ez a két felosztás különben hasonló is. A 2.9 ábra c rajza a szabályos hatszög alapelemű felbontást mutatja be. Ez a felbontás nem finomítható tovább hatszögekkel, e mellett nem is hasonló, ugyanis a 2.10 ábra tanúsága szerint a belőle szervezhető magasabb hierarchiaszinteknek (molekuláknak és sejteknek) csak egyike (az ábrán b-el jelölt) közelíti meg a szabályos hatszögalakot.

2.10 ábra - szabályos hatszög atomokból felépített molekulák és sejtek

 

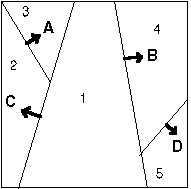
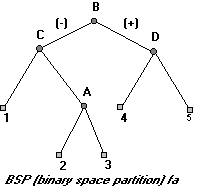
2.11 ábra - szabálytalan területfelosztás pozitív félterekkel

A számítástudomány bizonyos alkalmazásokban felhasználja a szabálytalan területfelosztást is, ilyenkor a legáltalánosabb esetben a területrészeket pozitív félterek határozzák meg. A 2.11 ábra első részén látható folytonos vonalak mutatják a félterek elválasztó vonalait. A vonalakra illesztett irányvektorok reprezentálják a pozitív irányt. A felosztás hierarchiáját az ábra második felén található Bináris Térfelbontási fa (BSP) reprezentálja. A területet két részre bontó B csomópontból (elválasztó vonalból) kiindulva a fán jobbfelé láthatók a pozitív térrészek, balra a negatívok. A B pozitív félterét ismét felbontja a D csomópont (elválasztó vonal), mely negatív fele a 4 területet, pozitív fele az 5 területet reprezentálja. Hasonló módon vizsgálhatjuk a B negatív félterét is.

Szintén "szabálytalan" felosztás, amely magasabb hierarchia szinteken fordulhat elő, ha a szabályos atomokat vagy molekulákat szabálytalan molekulákba illetve sejtekbe agglomerálják. Ezt a módszert általában a durva keresés meggyorsítására használják, ha a kérdéses objektum együttes két befoglaló mérete lényegesen különbözik egymástól. Ez utóbbi esettől eltekintve, a továbbiakban azt a leggyakrabban használt alapesetet tesszük részletesebb vizsgálat tárgyává, mely mind atomi, mind molekuláris , mind magasabb hierarchia szinten négyzet alakú.

Raszteres adatmodellek és tárolási modellek

A raszteres adatmodellek tulajdonképpen különböző típusú képek (fekete-fehér, szürkeségi értékekben tonusos, szines) digitális leírására szolgálnak. Az adatmodellnek alkalmasnak kell lenni arra, hogy vele közvetlenül műveleteket is végezhessünk a képekkel. Természetesen a képeket tárolni is kell. Vannak olyan modellek, melyekkel a képek tárolása gazdaságosabban végezhető. Ha ezek a modellek közvetlenül alkalmasok a műveletekre is, akkor nincs szükségünk arra, hogy ezeket a modelleket "tárolási" jelzővel lássuk el. Általában azonban nem ez a helyzet és a tulajdonképpeni és tárolási adatmodell elkülönül.

A térbeli adatok letapogatás (szkennelés) következtében közvetlenül raszteres formátumban jelennek meg az adathordozón. Ha a letapogatott képelemek x sorban és y oszlopban helyezkednek el, úgy az i.-ik sorban és j.-ik oszlopban található elemi négyzet helyét i és j, tulajdonságértékét pedig a Zij szürkeségi érték vagy színkód határozza meg. Az így létrehozott digitális képek azonban általában információs rendszerek feltöltésére közvetlenül nem alkalmasak, legfeljebb arra jók, hogy a képernyőn megjelenített vektor adatoknak képi (tónusos) hátteret szolgáltassanak.

A letapogatott adatokat automatikus képfeldolgozó eljárásokkal, interaktív szerkesztésekkel, egyéb forrásokból származó adatokkal való kiegészítéssel kell a további felhasználásra alkalmassá tennünk. E feldolgozás eredményeképpen az adatok fedvényekben, strukturáltan jelennek meg, azaz ugyanazt a területet több különálló térképre bontjuk, melyeket egyedenként logikailag összetartozó objektumok együttese alkot. Egy-egy fedvényen belül az objektumok homogének, s olyan egyedi objektumkóddal rendelkeznek, mely a relációs adatbázisban tulajdonságjellemzőikre mutat.

Mivel elvileg semmi sem korlátozza a fedvények számát, a tárolásmódok könnyebb megértése érdekében egyelőre úgy tekintjük, hogy a kép csak egy objektumot tartalmaz, mégpedig bináris objektumot, ami azt jelenti, hogy ha egy pixel értéke 1, úgy a kérdéses pixel része az objektumnak, ha pedig értéke 0, úgy a pixel az objektumon kívül van.
2.12 ábra - egyszerű objektum raszteres képe

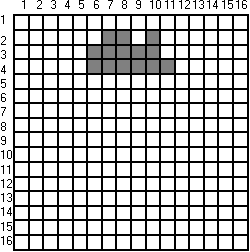
A bináris kép legegyszerűbb tárolása, ha a képmátrixot sor,- vagy oszlopfolytonosan kifejtjük, azaz (tárgyalásunkat az első esetre korlátozva) a képet alkotó 0-ákat és 1- eket sorfolytonosan egymás mellé írjuk, s e mellett, a rekord fejezetében megadjuk, hogy egy sor hány bit terjedelmű.

Példánk esetében tehát a rekordfejezet nélküli képleírás a következő: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 és még 197 db. 0.

(A bitek közötti szóközt csak a megjelenítő program kedvéért iktattuk közbe, hogy ott tudjon elválasztani, ahol szükséges).

 

Példánkból látható, hogy a közvetlen módszer nagyon sok fölösleges információt tárol. Ezt kiküszöbölendő számtalan tömörítő eljárást dolgoztak ki a bináris képek tárolására. Ezek közül a módszerek közül az alábbiakkal ismerkedünk meg:

Képtömörítő módszerek

Sorkifejtő kódolás (run-length encoding)

A módszer lényegében két eszközzel is csökkenti az eredeti sorfolytonos tároláshoz szükséges bitmennyiséget. Az első megtakarítás abból ered, hogy a 0 értékű biteket nem tárolja a másik pedig abból, hogy a sorban folytonos 1-eket a kezdő és befejező pixel oszlopindexével kódolja. Ahhoz azonban, hogy a módszer egyértelmű legyen még a kérdéses sorokat is kódolni kell, azaz össze kell kapcsolni a benne elhelyezkedő bitekre vonatkozó információkkal. Lássuk a módszert a 2.12 ábra egyszerű példáján:

2

7,8

10,10

3

6,10

 

4

6,11

 

A fenti adatmodell sokféle logikai struktúrában tárolható. Ránézésre talán az tűnhet a legegyszerűbbnek, ha az egész képet egy rekordban folyamatosan tároljuk, azaz:

2.12 ábra

2,7,8

2,10,10

3,6,10

4,6,11

volna a képet alkotó rekord formája. Ez az alak azonban megnehezítené a képen belüli keresést, gondoljunk csak arra, hogy egy 80 cm. x 80 cm.-es térképlap 40 mikrométer felbontással történő digitalizálása 20000x20000 képpontot jelent s ha a térképünkön csak egy darab 1 pixel vastagságú végigfutó függőleges vonal lenne ábrázolva az is egy olyan rekordot igényelne a fenti tárolás esetén, mely húszezer egyenkint három darab 5 jegyű számból felépülő szegmensből áll. Célszerűbb rekordképet úgy kaphatunk, ha a feladatot rekordon belüli és rekordok közötti láncolással, indexlistás szervezéssel esetleg relációs táblázatok kialakításával oldjuk meg. A szkennerek rendszerint, beépített mikroprogram választékuk segítségével, a kívánt formátumban szolgáltatják a bináris képet.

Az IDRISI Oktató Anyagban megismert "csomagolt" (packed) formátum szintén ezzel a módszerrel tömörít, a különbség csak az, hogy egyrészt a képek értéke nem csak 1 lehet, másrészt a fejezetet a képfájlhoz rendelt különálló fejezet fájlban helyezi el.

Lánc kód (chain codes)

Válasszuk meg az objektum kezdőpontját valamelyik határon fekvő pixelének bal felső sarkaként. A kezdőpontot a kérdéses pixel sor-, és oszlop koordinátáival (i,j) jelöljük. Az objektumot a továbbiakban kezdőpontjából kiindulva a kerületét alkotó egységvektorokkal írjuk le. Az egységvektorokat az égtájaknak megfelelően az alábbiak szerint kódoljuk: Kelet=0, Észak=1, Nyugat=2, Dél=3. (Megjegyezzük, hogy a későbbiekben meg fogunk ismerkedni az általánosított, 8 irányra kiterjedő lánckódolás alapjaival is).

Mivel egymás után több azonos irányú egységvektor is szerepelhet, célszerű ha a rekordot úgy építjük fel, hogy minden egységvektor után megadjuk az ismétlési számot is. A határleírást meghatározott sorrendben pld. az óramutató járásának megfelelően kell végrehajtani.

A 2.12 ábrán látható objektum ebben a rendszerben a következő rekordba kódolható:

02,7

0,02

3,01

0,01

1,01

0,01

3,02

0,01

3,01

2,06

1,02

0,01

1,01

Minél kisebb az objektum kerületének és területének viszonya annál nagyobb helymegtakarítást eredményez a módszer.

Míg a sorkifejtő kódolás és természetesen a teljes bináris mátrix sorfolytonos tárolása is a teljes képet tárolta, addig a lánc-kód egy képen belüli objektumra vonatkozik. Ez a tulajdonsága jelentősen megkönnyíti az objektumonkénti lekérdezést.

A módszer tömörítési képessége igen előnyös; bizonyos műveletek végrehajtására mint például a terület és kerület becslésére, erős törések és konkávitások detektálására közvetlenül is alkalmas a lánckód. A nehézségek a gyakran előforduló halmazműveleteknél (unió, metszés stb.) lépnek fel, ilyenkor célszerű az objektumot a lánckódból az eredeti bináris mátrixba konvertálni a műveletek végrehajtása előtt.

Középtengely transzformáció (medial axis transformation)

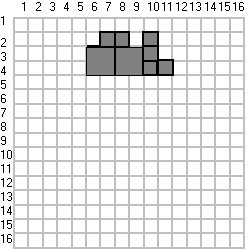
A módszer lényege, hogy az objektumot a benne található legnagyobb négyzetekre bontjuk, és az így kapott különböző nagyságú négyzetek kezdőpontjainak koordinátáival (kezdőpontként vagy a bal felső sarkot, vagy a középpontot választva) és a kezdőpontokhoz tartozó négyzetek nagyságával (hányszorosa az oldala az eredeti pixelméretnek) írjuk le.
2.13 ábra - a 2.12 ábrán látható objektum blokkosítása

Az objektumot a következő számsorozattal tárolhatjuk:

02,07,01 02,08,01 02,10,01 03,06,02 03,08,02 03,10,01 04,10,01 04,11,01

A tárolási hely igény tovább csökkenthető, ha egy rekordban összefoglaljuk az azonos méretű négyzetek kezdőponti koordinátáit.

E tömörítési módszer előnyös a halmazműveletek (unió, metszés stb.) közvetlen végrehajtására is.

Négyágú fa (quadtree)

A quadtree módszer napjaink legkorszerűbb, legelterjedtebb raszteres adattömörítő eljárása. Legfőbb előnye, hogy elvileg lehetővé teszi tetszőleges felbontású (finomságú) képek tárolását. Nem hanyagolható el az a másik előnye sem, hogy éppen perspektív jellemzőinek betudhatóan, a módszerre vonatkozó algoritmusok tárháza igen gazdag. A téma iránt érdeklődők szinte minden problémára megoldást találnak SAMET monográfiáiban [4], [5].

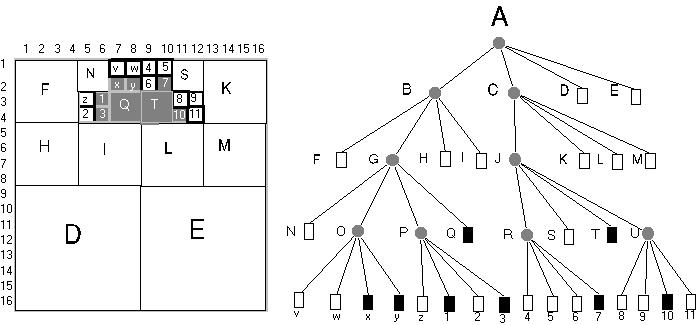
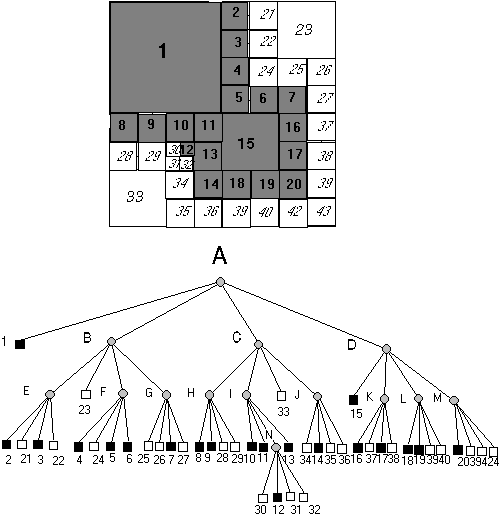
2.14 ábra - egyszerű alakzat quadtree stuktúrája

A módszer lényegét a 2.14 ábrán mutatjuk be. Bontsuk fel az A négyzetet négy egyenlő részre és nevezzük el ezeket a negyedeket B, C, D, E-nek. Amint az ábrából látható D és E nem tartalmaznak fekete pixeleket azaz üresek, következésképpen tovább bontásra nem szorulnak. A tovább bontásra nem szoruló négyzeteket a gráfban levélnek nevezzük és annak megfelelően, hogy üresek e vagy sem fehér vagy fekete négyzettel jelöljük.

Példánkban tehát D és E üres levelek és a fa alakú gráfban fehér négyzetekkel vannak jelölve. Érdemes már most felfigyelnünk arra a tényre, hogy a fában elfoglalt hely egyértelműen meghatározza a kérdéses levél nagyságát és a képen belüli elhelyezkedését.

Az említett D és E levelek a gyökér (A) után következő tehát második hierarchiaszinten vannak, mely szinthez tartozó négyzet oldalhossza az eredeti kép oldalhosszának fele.

Megállapításunkat célszerűen általánosíthatjuk is: legyen az eredeti kép oldalhossza s=2m, a hierarchiaszint h, úgy a h hierarchiaszinthez tartozó négyzet oldalhossza s(h)=2(m-h+1).

A képen belüli helyet a hierarchia színt illetve a levélhez a gyökérből vezető ágak sorszámai egyértelműen meghatározzák. Vegyünk fel a 2.14 ábrán látható módon egy olyan koordináta rendszert, melyben az origó a kép bal felső sarkára illeszkedik. A +Y tengely mutasson Délre, a +X tengely pedig Keletre. Jelölje l(h) a (h-1) csomópontból kiinduló ág sorszámát balról jobbra növekvő sorrendben (azaz a baloldali ág 1, a jobboldali ág 4 sorszámot kap). A sorszámok megállapodás szerint a következő égtájaknak felelnek meg: 1=ÉNY, 2=ÉK, 3=DNY, 4=DK.

Most már megkísérelhetjük, hogy a levelekben reprezentált négyzetek bal felső sarkainak koordinátáira általános érvényű kifejezéseket állítsunk össze:

(4)

(5)

Térjünk vissza a 2.14 ábra tanulmányozására!

A második hierarchia szinten a már megtárgyalt D és E fehér leveleken kívül még két csomópontot is találunk (jelölésük B és C). A csomópontokat az különbözteti meg a levelektől, hogy olyan területeket reprezentálnak, melyek részben fehérek részben feketék (ezért is szokták a csomópontokat szürkéknek nevezni), és ezért még további felbontásra szorulnak.

A képet leíró négyágú fa eltolás érzékeny, azaz ugyanazt az objektumot más és más fával tudunk ábrázolni annak a függvényében, hogy kezdőpontja a kép origóhoz képest milyen helyzetet foglal el.

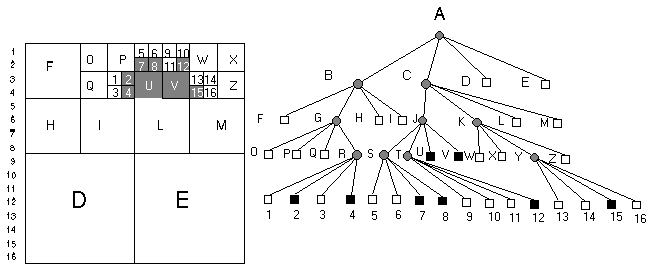
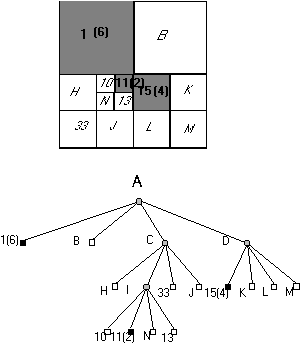
2.15 ábra - a képeltolás hatása quadtree struktúrára

A 2.15 ábrán példa objektumunkat két pixellel Kelet felé toltuk s ennek hatására az objektumot leíró fa gyökeresen megváltozott - jelentősen egyszerűsödött. Az eltolás érzékenység előnytelen tulajdonság ezért az alább ismertetendő tömörítő eljárások egy jelentős része az eltolás érzékenység csökkentését is megcélozta.

A hierarchikus állományok tárolására az első részben ismertetett logikai adatstruktúrákat használják. A keresési eljárásokra is tekintettel, rendszerint az ágak menti kétirányú cimláncolást alkalmazzák.

Lineáris négyágú fák (linear quadtrees)

Ez a pointer nélküli reprezentáció a tömörítést azzal éri el, hogy a fehér leveleket nem tárolja. Minden fekete levél számára egy kódolt ösvényt ad meg a fában, mely hossza attól függ hányadik hierarchia szinten helyezkedik el a levél. Kódolásra a négyes számrendszer számjegyeit alkalmazza a módszer : 0 = ÉNY, 1 = ÉK, 2 = DNY, 3 = DK.

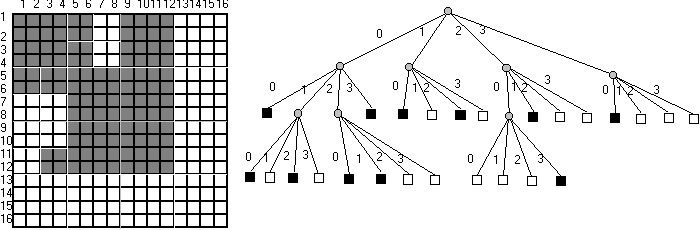
2.16 ábra - egyszerű alakzat lineáris quadtree kódolása

A 2.16 ábra egyszerű alakzatát a következő kódkombinációval írhatjuk le: 00, 010, 012, 020, 021, 03, 10, 12, 203, 21, 30. A módszer előnyei közül megemlítjük, hogy ASCII kódba alakítva egyszerű szövegként továbbítható, két lineáris quadtree között könnyű a halmazműveletek végrehajtása és könnyű belőle az eredeti képet helyreállítani. Külön figyelmet érdemel, hogy a négyes alapú számrendszerben az úgy nevezett mozaik aritmetika szabályait felhasználva egyszerű algoritmusok dolgozhatók ki a fán történő keresésre, a szomszéd egységek megkeresésére, stb. A részletek iránt érdeklődőknek ajánlom a magyar nyelvű NCGIA Core Curriculum 2. kötet ([6a]) 37. fejezetét.

Négyágú fa normalizálás (quadtree normalization)

Amint arról már történt említés, valamely objektum négyágú fa ábrázolása érzékeny az eltolásra, azaz ha az objektumot x vagy y irányban mozgatjuk a quadtree csomópontok száma megváltozik. A fenti tényből következik, hogy váltakozó x és y irányú eltolásokkal létrehozhatjuk azt az optimális helyzetet, melyben a képet ábrázoló quadtree csomópontjainak száma minimális. Az optimalizálás esetenként megkövetelheti a hálóméret megduplázását.

A módszert gyakran nem képek, hanem a képekből kiválasztott objektumok normalizálására használják. A gyakorlati alkalmazások során különböző típusú repülőgépek különböző, súlyponttal és főtengelyekkel jellemzett quadtreejeit normalizálták azzal a céllal, hogy összehasonlítva őket a repülőgép megfigyelő videó rendszer zajos képével alakfelismerést hajtsanak végre és meghatározzák a megfigyelt objektum típusát. Ebből az alkalmazásból számunkra elsősorban az objektum és a háttér különválasztása érdekes, mely fogást más tömörítő eljárás is alkalmaz.

Négyágú fa középtengelytranszformáció (quadtree medial axis transformation)
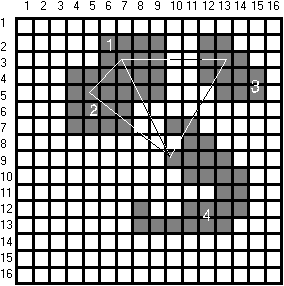
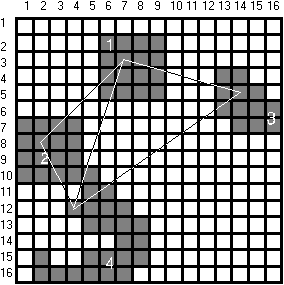
2.17 ábra - alakzat középtengely transzformáció előtt

2.18 ábra - alakzat középtengely transzformáció után

 

A 2.17 és 2.18 ábrákon egy kép négyágú fa felbontását és annak középtengely transzformáltját ábrázoltuk.

A módszer az előzőekben ismertetett középtengely transzformáció alkalmazása a négyágú fa felbontásra.

A módszer első lépésében fekete tömbökre bontjuk a képet és megállapítjuk a tömbök "sugarát". Sugár alatt azt a legkisebb távolságot értjük, mely a tömb középpontjától x vagy y értelemben, pixel mértékegységben kifejezve, a fehér tömbök határáig tart. A fekete tömb a kép határain túl is terjedhet, ezért úgy képzeljük el, hogy a kép szélein túli terület fekete.

A tömböket sugárméretük szerint növekvő sorrendbe állítjuk és ezután az első (legkisebb sugarú) tömbtől kezdődően sorra megnézzük, hogy a kérdéses tömb része-e valamelyik magasabb sorszámú tömbnek. Amennyiben része úgy a transzformált quadtreeből kiesik, amennyiben nem, úgy a transzformált gráf egy levelét fogja alkotni. A megmaradt blokkokat eredeti helyükön és eredeti méretben szerepeltetjük az ennek megfelelően negyedelt képen, de melléjük írjuk sugaraikat is. A képből aztán elkészítjük a szokásos szabályoknak megfelelően a transzformált gráfot.

A kép helyreállítása a transzformált képből igen egyszerűen hajtható végre: a sugáradatoknak megfelelően kiegészítjük a megmaradt tömböket. Az eredmény az eredeti kép lesz, ha a kétszeresen takart fekete pixeleket is csak közönséges fekete mezőknek tekintjük.

A módszer általában jelentősen csökkenti a csomópontok számát s ezzel nem csak tárolóhelyet takarít meg, de csökkenti az eltolásérzékenységet is.

Négyágú fa erdők (quadtree forests)

Az eredeti fát felbontjuk olyan fák listájára (ezt nevezik tulajdonképpen erdőnek), mely fák az eredeti struktúra kisebb - nagyobb részei. A felbontáshoz egy rekurzív algoritmussal úgy címkézik a levél- és csomópontokat, hogy minden fekete levél jó ugyancsak jó minden szürke csomópont, ha legalább két jó fia van. Minden egyéb csomópont rossz.

Ezután leválasztják a rész-fákat a legmagasabb jó pontjuktól kezdődően. Ha a gyökér jó, marad az eredeti struktúra.

Minden belépés az erdőbe pointert tartalmaz a rész-fa kezdő jó csomópontjára, valamint szint és út információt (ez utóbbi erősen hasonlít a lineáris quadtreere), mely pozícionálja a részletet az eredeti fa struktúrában. Maga a rész-fa lista topológia nélküli lineáris lista.

A módszer csak részben csökkenti a tárolandó fehér levelek számát és nem küszöböli ki a négyágú fa felbontás eredendő problémáit: az eltolás érzékenységet és azt a tényt, hogy nem tudja kihasználni egy képen belül a koherrenciát (azonos elemi formák ismétlődését).

Négyágú fa hálók (quadtree meshes)

Ha a képtartalom több egyező vagy különböző képrészletből áll igen gazdaságos a képeket quadtree hálókban tárolni. A módszer további előnye, hogy érzéketlen az eltolásra.
2.19a ábra - alakzat eltolás előtt

2.19b ábra - alakzat eltolás után

2.20 ábra - alakzat elemekre bontása

Első lépésben bontsuk fel a képet az azonos illetve különböző képelemekre és készítsük el az egyes elemek négyágú fáit. Kapcsoljuk össze a képelemeket egy hálózattal mely megvalósítási formája a lineáris listától az optimális Delaunay háromszögelésig terjedhet. A teljes kép tárolása még hat további adatot igényel, ezek a következők: a befoglaló négyzet nagysága (pixel egységben, 2 valamelyik hatványa); a befoglaló négyzet bal felső sarkának képkoordinátái; a képrészlet súlypont relatív koordinátái a befoglaló négyzet bal felső sarkához képest; a képrészletek esetleges quadtree tömörítő eljárásának a kódja.

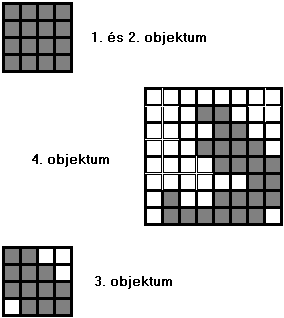
A 2.19 a és b ábrán egy négy képrészletből álló hálózattal összekapcsolt képet látunk a képrészletek eltolása előtt és az eltolás után.

A 2.20 ábrán a négy képrészlet látható befoglaló négyzetében. Mivel az 1 és 2 objektum azonos, befoglaló négyzetük méretét és négyágú fáját csak egyszer kell tárolni. A 2.19 ábra baloldali objektuma hagyományos quadtree esetén 143, a jobboldali 103 levél tárolását igényli. A négy objektum quadtree együttesen 52 levelet tartalmaz. Még ha figyelembe vesszük a kiegészitő adatokat is a megtakarítás szembetűnő.

A módszer mindössze néhány éve került publikálásra, alapvető problémája az optimális képrészlet nagyság kialakítása, melyre vonatkozó kutatások jelenleg is folynak. Annyit már sikerült megállapítani, hogy előnyös, ha a képrészletek közel azonos méretűek. Nem nehéz arra a következtetésre jutni, hogy az eredetileg képek tárolására kidolgozott módszer további finomítása bevezetheti a raszteres modellek közé is a vektoros modellekben általános objektum fogalmat.

A raszteres modellt használó rendszerek túlnyomó többsége ugyanis csak a pixelt tekinti önálló egységnek. Ha azonban az azonos attribútumú pixelekből álló részleteket amúgy is ellátjuk kiegészítő információkkal, semmi akadálya annak hogy ezeket kiegészítsük még egy objektum azonosítóval.

A módszer kiterjeszthető különböző szürkeségi fokozatokat tartalmazó képek tárolására is, ami tulajdonképpen azt jelenti, hogy a kérdéses attribútum értéket kiegészítő változóként kapcsolja az alakzathoz.

ˇ         a következő részben áttekintjük a vektoros adatok tárolását,

ˇ         visszatérhet az előző részhez is,

ˇ         vagy a tartalomjegyzékhez.

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc