Térinformatika

Az adatszervezés alapkérdései

E címszó alatt a tárolási és keresési eljárásokat szeretnénk röviden összefoglalni. Meg kell jegyeznünk, hogy míg az elektronikus számítógépek adatszervezési fölhasználásának kezdetén a logikai és fizikai adatszervezés nem vált külön, e két feladatkör gyakorlatilag párhuzamosan volt tárgyalható. A korszerű adatbázis koncepció megjelenésével a logikai és fizikai adatbázis szervezés különvált, s így a tárolás mely a fizikai adatszervezés része, különvált a logikai szinten végrehajtható adatkeresési eljárásoktól. Nem tekintjük feladatunknak a fizikai adatszervezési eljárások részletes vizsgálatát, mivel ezeket az operációs rendszerek gépfüggően oldják meg az alapelérési módszerek segítségével. Tekintettel azonban arra, hogy már többször hivatkoztunk az alapelérési módokra, röviden össze szeretnénk foglalni a fizikai tárolás alapmódszereit is.

A legkézenfekvőbb tárolási eljárás az úgynevezett folyamatos tárolás. A folyamatos tárolás lehet:

Soros tárolás: Ez alatt azt értjük, hogy a rekordokat a filen belül keletkezésük sorrendjében egymás után helyezzük el. Lényegében ez a tárolási eljárás analóg azzal, ahogy a könyvtárakban beérkezésük után a különböző könyveket elhelyezik. Problémát jelent ugyanakkor ennél a tárolási módnál, ha a file-t bővíteni akarjuk, ebben az esetben ugyanis a folyamatosan tárolt rekordokat el kell tolni és az egész tároló betöltését meg kell változtatni.
Szekvenciális tárolásnak nevezzük azt a folyamatos tárolási módszert, amikor a file rekordjait valamely rendezési elvnek megfelelően helyezzük el egymás után a tárolóban. Ez a rendezési elv rendszerint a felhasználás gyakorisága lehet, azaz azokat a rekordokat helyezzük el a file elején, melyek leggyakrabban kerülnek felhasználásra. Ennek a tárolási módnak két hibája van: az első és legfontosabb az, hogy a gyakoriságot a betöltés előtt általában nem ismerjük, ennek megfelelően csak olyan feltételezések alapján végezhetjük el a betöltést, melyeket a gyakorlat később megcáfolhat, ez pedig azt a következményt vonja maga után, hogy a betöltést meg kell változtatni. A második probléma azonos a soros tárolásnál fennálló problémával, újabb rekordok megjelenése esetén a tárolási strukturát meg kell változtatni. Ez a karbantartási munkákat jelentősen megnöveli.

A leggyakrabban alkalmazott tárolási eljárások a szórt tárolások csoportjába tartoznak. A szórt tárolásokat is két alcsoportra osztjuk:

A hiányjelző táblázatok alapján történő tárolás. Minden tároló egység rendelkezik egy táblázattal az adott operációs rendszerben, mely jelzi azokat az üres területeket, melyek még betöltésre várnak. Az újabb rekordok megjelenése során e táblázat felhasználásával történik a rekord elhelyezése. Lehetőleg arra kell törekedni, hogy az elfoglalt tárolóhely megközelítse az igényelt tárolóhely méreteit.
A legközismertebb formája a szórt tárolásnak az úgynevezett indirekt címzéssel történő tárolás. Ennek a tárolási módszernek az a lényege, hogy a rendezési fogalomból különböző képletek segítségével tároló címeket gyártanak és a rekordokat ezeken a címeken helyezik el. Ennek a tárolási módszernek az a problémája, hogy a rendezési elv és a tárolóhelyek között nem lehet olyan képletet gyártani, mely biztosítja, hogy valamennyi tárolóhely betöltésre kerüljön és csak egy rekord által, hanem előfordul az, hogy más és más rendezési elvnek ugyanaz a tároló cím felel meg a képletek alapján. Ebben az esetben úgy járnak el, hogy a már betöltött tárolóhelyen szabadon hagyott rekeszekbe megjelölik azt a helyet, ahová az úgynevezett túlcsordulási területen a kérdéses rekordot elhelyezik. ily módon - amint azt majd a keresési eljárásoknál látni fogjuk - a fizikai cím megkeresése után a kereső programnak lehetősége van arra, hogy a címen tájékoztatást kapjon a rekord túlcsordulási területen történő elhelyezkedésére.
A legtökéletesebb tárolási módnak a szekvenciális tárolás és szórt tárolás összekapcsolását tekinthetjük. Ebben az esetben ugyanis elkerüljük a szekvenciális tárolásnak azt a hátrányát, hogy karbantartás során új rekord megjelenésekor a tárolt rekordokat át kell helyezni, hogy a rendezési fogalomnak megfelelő helyet az új rekord megkaphassa. Ekkor ugyanis a kezdeti betöltés során szekvenciálisan történik a rekordok elhelyezése, karbantartáskor azonban az új rekord beszúrása helyett csak egy utalás kerül beszúrásra a rendezési fogalom megelőző értékéhez tartozó rekord után, mely arra utal, hogy a kérdéses és a logikailag következő rekord hol található a túlcsordulási területen.

A keresési eljárások mind a fizikai mind a logikai adatbázisban fölhasználhatók. Mivel mi elsősorban a logikai adatszervezés kérdéseivel kívánunk foglalkozni, ezért a keresési eljárásoknál a rekordok virtuális tehát logikai elhelyezkedése alapján fogjuk végezni a keresést. Amikor tehát a rekord tároló helyéről lesz szó, ezt úgy kell értenünk, hogy melyik az a relatív hely, amelyet a rekord a logikai file-ban elfoglal. A fentiekből következik, hogyha a tárolás alatt azt értjük, hogy hogyan építjük fel a logikai file szerkezetet, úgy a fizikai tárolással kapcsolatban ismertetett eljárásoknak ebben a felépítési folyamatban is hasznát vehetjük.

A fizikai rekordok tárolásánál csak a rendezési elvet vettük figyelembe. A klasszikus adatfeldolgozási rendszereknél a keresési eljárások is csak a rendezési fogalom, az úgynevezett elsődleges kulcs alapján működtek. A korszerű integrált adattárolási rendszerek lényege azonban az, hogy a keresés ne csak az elsődleges, hanem a másodlagos kulcsok alapján is végrehajtható legyen. Ez indokolja a keresési eljárások alábbi felosztását.

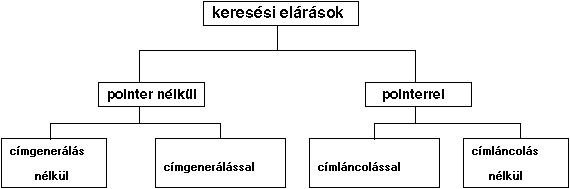
1.9 ábra - keresési eljárások osztályozása

Szekvenciális keresés.

A szekvenciális keresési eljárás során a kereső program rendelkezésére bocsátjuk a keresési argumentumot, azaz a rendezési fogalomnak azt az értékét, melyhez tartozó rekordra szükségünk van, ezután a program folyamatosan az első rekordtól kezdődően összehasonlítja a keresési argumentumot az adott rekord rendezési fogalmával és ezt mindaddig végzi, amíg egyezést nem talál a keresési argumentum és a rekordok rendezési fogalma között.

Fentiekből látható, hogy ez a keresési eljárás igen nagy időszükségletű, különösen abban az esetben, ha a tárolás soros módon került végrehajtásra.

Az m út keresés esetében a megvizsgált file-t m darab egyenlő részre osztjuk. A keresés úgy történik, hogy a program összehasonlítja a keresési argumentumot az egyes részek utolsó rekordjának rendezési fogalmával. Amennyiben a rendezési fogalom kisebb a keresési argumentumnál, úgy megnézi a következő rész utolsó rekordjának rendezési fogalmát és így tovább. Miután elérte annak a résznek az utolsó rekordját, melynek rendezési fogalma nagyobb a keresési argumentum értékénél, akkor visszaugrik az adott rész első rekordjára és a keresés a továbbiakban szekvenciálisan hajtódik végre.

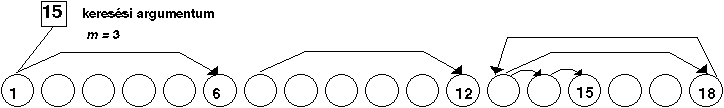
1.10 ábra - m út keresés

Amint az a keresési folyamat leírásából következik, ez a módszer kizárólag szekvenciálisan tárolt rekordok esetében alkalmazható. Keresési ideje rövidebb, mint a szekvenciális keresésé.

A szekvenciálisan, tehát a rendezési fogalom növekvő értékei szerint tárolt rekordok esetében a bináris keresési eljárás a legcélravezetőbb. Lényege a következő: a keresési argumentum először a tárolt rekordok felezőjében elhelyezkedő rekord rendezési fogalmával kerül összehasonlításra. Amennyiben ennek a rekordnak a címe nagyobb, úgy a keresett rekord a file első felében, amennyiben kisebb, úgy a file második felében fog elhelyezkedni. Ezután a kiválasztott félrészt ismét felezi a keresőprogram és ezt a felezési műveletet mindaddig folytatja, míg a szükséges rekordot meg nem találja.

1.11 ábra - bináris keresés

Az eddig ismertetett keresési eljárások összehasonlították a keresési argumentum, értékét a rekordok rendezési fogalmaival. A most ismertetendő két keresési eljárás kiszámítja a keresett rekord címét és a kiszámított címet közvetlenül kihozza a tárolóból, illetve kiválasztja a logikai file-ból a kapott sorszámú rekordot.

A direkt címzéses módszernél a keresési argumentum egy rendezési fogalom értéke. Alkalmazása csak akkor lehetséges, ha a tárolás is ezen elv alapján szekvenciálisan történik. A módszer elvi alapja az, hogy a rendezési elv számértéke megegyezik a tárolóhely címével. Például: diszk memórián történő tárolás esetén az első helyérték a lemezköteg számát, a 2-4 helyértékek a cilinderszámot, az 5. helyérték pedig a sávszámot jelenti. Ez a keresési eljárás tehát szorosan kötődik a meglévő lemezegységek számához és méreteihez. Akkor lehetne kihagyások nélkül alkalmazni, ha 10 lemezköteg 999 cilinder és 10 sáv állna a tárolás, illetve a keresés rendelkezésére. Logikai szerkezetben a módszer csak akkor alkalmazható, ha a kapott relatív címek (sorszámok) folyamatosan lefedik a tartományt.

Az adatszervezés korai szakaszában sokkal nagyobb gyakorlati jelentősége volt az indirekt címzésnek. E módszer alkalmazása esetén, ha a rendezési fogalomban ugrás van, esetleg nincs ugrás, de nincs valamennyi sorszám kitöltve, osztályozó kódok, vagy alfanumerikus címzés esetén algoritmust kell kidolgozni, mely a rendezési fogalom értékeiből bizonyos tartományba eső egyenletes tároló-címeket vagy relatív címeket (sorszámokat) számol.

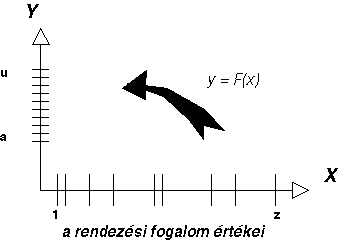
1.12 ábra -az indirekt címzés alapelve

Sajnos olyan algoritmust, mely a kitűzött célt maradéktalanul megvalósítja, általában nem sikerül kidolgozni, és ez azt eredményezi, hogy az adott tartományban nem minden tároló-cím kerül betöltésre, illetve olyan címek is találhatók, melyekre több betöltendő rekord is esik. Ilyen esetekben a második, harmadik stb. betöltéskor a számított tároló-címre csak egy megjegyzést helyezünk el, mely megmondja, hogy az adott rekord a túlcsordulási területen hol helyezkedik el.

A jellemzők kombinációja alapján történő keresés olyan indirekt címzés, ahol a cím kiszámításának alapjául bizonyos jellemzők számjegyekkel történő leírásának kombinációi szolgálnak; ebben az esetben tehát a címet nem csupán a rendezési fogalom segítségével dolgozzuk ki, hanem a különböző mezőkben tárolt tulajdonság jellemzők kombinálásával. Többé kevésbé ez az eset a vektor struktúrák tárolása kapcsán ismertetendő hashing módszer esetében is. A 70-es évek végén több szerző tett kísérletet arra, hogy képleteket adjon a tárolási, illetve keresési cím ilyen módon történő kiszámítására. Megállapíthatjuk ugyanakkor, hogy akkor ez a módszer még nem terjedt el. Ez a tény azzal magyarázható, hogy a tartalom szerinti visszakeresés legegyszerűbben a pointeres visszakereső módszerekkel valósítható meg. A pointerek vagy mutatók olyan útjelzők, melyek elvezetnek egy adott mezőhöz, vagy rekordhoz egy másik helyen található mezőből vagy rekordból. A fizikai adatszervezésben a pointer mindig a célrekord gépi címe. A logikai adatszervezésben kétféle pointert különböztetünk meg. A pointer lehet valamely rekordnak file-on belüli relatív címe, azaz sorszáma. Lehet ugyanakkor pointer valamely mező tartalma is, amennyiben az adott mezőtartalom egyértelműen meghatároz minden rekordot a file-ban. Az ilyen mezőtartalommal megegyező pointereket szimbolikus pointereknek is nevezik.

A láncolásos módszerek lényege az, hogy minden adategység, esetünkben rekord, után feltüntetik az adott rekordot logikailag megelőző, illetve logikailag követő rekordra mutató pointert. Ez a kettős láncolás, amikor tehát mind a ligikailag megelőző, mind pedig a logikailag követő rekord címét tároljuk, a legáltalánosabb eset. Elképzelhető az az egyszerűbb eset is, amikor vagy csak a logikailag megelőző, vagy csak a logikailag követő rekordok címe kerül az adott rekord után rögzítésre. A láncolás általában nemcsak egy, hanem a korszerűbb integrált adatkezelő rendszerekben, több szempont alapján is történik, ezért ahhoz, hogy valamely szempont alapján történő láncoláson végig tudjunk menni, mindenekelőtt meg kell keresni az adott szempont szerinti láncolás kezdőcímét, az úgynevezett horgonycímet.

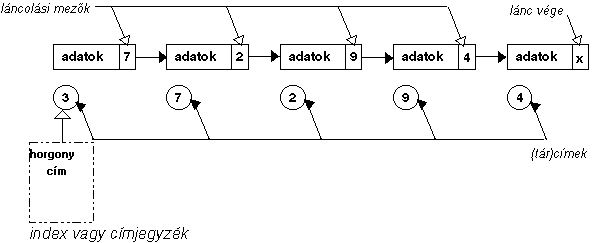
1.13 ábra - a láncolásos módszer elvi vázlata

Gyakran az utolsó rekordot teljes gyűrűt alkotva, a ciklikus adatmodellben megismertek szerint, visszaláncolják az első rekordhoz.

1.14 ábra - ciklikus láncolás

A láncolásos keresési módszereket többféleképpen is osztályozhatjuk, mindenekelőtt aszerint történhet az osztályozás, hogy a láncolást milyen adategységek között végezzük. Így beszélhetünk

több file rekordjai közötti láncolásról,
egy filen belüli láncolásról,
és rekordon belüli láncolásról.

A több file rekordjai közötti láncolásra jó példa az egy személy tulajdonát képező földrészletek kikeresése. Ha ugyanis a földrészletek földrajzi egységenként külön-külön file-okba vannak, akkor az egy személy tulajdonát képező különböző helyeken található földrészleteket csak úgy tudjuk összegyűjteni, ha ezeket több file rekordjai közötti láncolással tároljuk, illetve keressük. Hasonló példa, mely gyakorlati jelentősége még nagyobb, az egy személy részére különböző helyeken történő kifizetések összegyűjtése és egységes megadóztatása.

A file-on belüli láncolásnak három alcsoportját különböztetjük meg:

Rekordok közötti láncolás a rendezési fogalom növekedése szerint. Erre a láncolásra akkor van szükség, ha a rekordokat szórtan tároljuk, ugyanakkor a keresést szekvenciális módszerrel kívánjuk elvégezni.

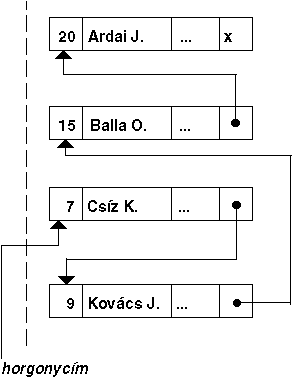
1.15 ábra - láncolás a rendezési fogalom növekedése szerint

Rekordok közötti láncolás egyes mezők tartalma szerint. Erre a láncolási típusra jó példát szolgáltathat a személyi file (1.2 táblázat). Amint a táblázatból látjuk, ez a láncolási típus kétféleképpen valósítható meg:

beszélhetünk teljes láncról és
részláncról.

A másodlagos kulcsok szerinti lánckezdő címeket külön file-ban tároljuk. Amint a táblázatban közölt példából látjuk, a teljes lánc kialakítását egy olyan rendezési fogalom, mint a fizetés alapján hajtottuk végre a lánckezdő cím ebben az esetben a legkisebb fizetéssel rendelkező 6-os rekordcím, a következő a 2-es, a következő a 7-es és végül a legnagyobb a 8-as. Végezhetünk ugyanezen a példán részláncolást is. Itt az egyes költséghelyek szerinti rekordokat kapcsoltuk össze.

mezőnév - rekord cím	azonosító szám	költséghely	láncolási mező - költséghely	fizetés Ft-ban	láncolási mező - fizetés
1	100	10	3+	123000	10
2	106	20	6+	85000	7
3	110	10	7	190000	8
4	111	30	5+	160000	9
5	117	30	8	140000	4
6	120	20	9	74000	2+
7	121	10	x	87000	1
8	124	30	10	240000	x
9	130	20	x	160000	3
10	133	30	x	134000	5

+ = a lánc első eleme; x = a lánc vége

1.2 táblázat - teljes és rész láncolás a fizetési jegyzékben

Fölé- és alárendelt rekordok láncolása. Igen szemléletes példája a hierarchikus rekordok láncolásának a gyártmányjegyzék szerkesztése. A gyártmányjegyzék külön rekordban foglalja össze a készgyártmányokat, a félkész termékeket és az alkatrészeket. Mivel a készgyártmányok félkész termékekből állnak, ezért a készgyártmányokat csak a hierarchiában alárendeltebb félkész termékekhez láncoljuk. Az alkatrészek esetében a helyzet fordított, ugyanis ezek csak a magasabb hierarchiájú félkész termékekhez láncolódnak. A félkész termékek azonban, melyek a hierarchia közepén helyezkednek el, mind a logikailag fölérendelt, mind a logikailag alárendelt rekordokhoz is láncolódnak

A rekordon belüli láncolás. Ez a láncolás tulajdonképpen a hierarchikus rekordok fizikai tárolására ad lehetőséget. Mint említettük, a fizikai és logikai rekordok között az eddigiek folyamán is mindig különbséget tettünk, abból a meggondolásból kiindulva, hogy általában nem célszerű a fizikai rekordot egy bizonyos hierarchia alapján tárolni, azaz nem célszerű a fizikai tárolás során egy bizonyos hierarchiát előnyben részesíteni, mivel ez megnehezíti más hierarchiák érvényre jutását. Elképzelhető azonban olyan eset is, mikor a tárolt információnak csak egy hierarchikus felépítését kívánjuk a felhasználás folyamán érvényre juttatni. Ilyen esetekben igen nagy megtakarítást eredményez, ha a rekordot fizikailag is hierarchikusan tároljuk. A rekordon belüli hierarchiát master és detail láncokon keresztül érvényesítjük. A különböző hierarchia szinteket a master láncok kapcsolják egymáshoz, míg az azonos szinteken a láncolás a detail láncok segítségével megy végbe. A gyakorlatban működő rendszereknél maximum 15 hierarchia szintet alkalmaznak. Lényeges megjegyezni, hogy a hierarchikus rekordokat minden szinten egymással is lehet láncolni és ily módon biztosítani az integrált adatkezelés lehetőségét.

A láncolással kapcsolatos ismereteinket próbáljuk életszerűbbé tenni az 1.6 illetve 1.7 ábrán látható adatstruktúrák adatszervezési leírásával.

Nézzük meg mindenekelőtt az 1.6 ábrán látható fa-struktúrát és azt, hogy milyen módon tudjuk a struktúrát tárolni, illetve visszakeresésre alkalmassá tenni. Ha nem vesszük figyelembe a struktúrában található hierarchiákat, akkor a klasszikus adatfeldolgozás szabályai szerint a ponton végzett észleléseket és azok eszközeit az 1.3 táblázat formájában tárolhatjuk. Feltűnő, hogy ebben a tárolási módban igen sok adatot többszörösen tároltunk, ezért a tárolóhely kihasználásunk igen rossz.

A	B1	C1	D1	E1
A	B1	C1	D2	E2
A	B1	C1	D3	E3
A	B1	C1	D3	E4
A	B1	C1	D3	E5
A	B1	C2	D4	E6
A	B2
A	B3	C3	D5	E7
A	B3	C3	D6	E8
A	B3	C4	D7	E9
A	B3	C4	D7	E10
A	B3	C4	D7	E11

1.3 táblázat - észlelési rekord hagyományos tárolási struktúrában

Ha a hierarchiákat figyelembe vesszük és lineáris folytatólagos tárolási módszert alkalmazunk, úgy a tárolást az 1.4 táblázat szerint végezhetjük. Ennél a tárolási módnál az egyes hierarchiaszinteket kódolással tüntethetjük ki és ily módon az eredeti fa- struktúrában rejlő előnyöket kihasználhatjuk.

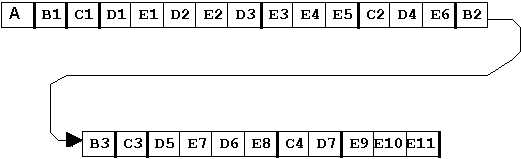
1.4 táblázat - hierarchikus észlelési rekord folytonos tárolási struktúrában

Szórt tárolás esetén az azonos típusú mennyiségeket közös csoportokban vonva tárolhatjuk. Ha tehát feltételezzük, hogy például 3 állásponton hajtottuk végre az észleléseket, úgy az 1.5 táblázatban található szórt tárolási módszerrel tárolhatjuk a megfigyelési értékeket, a műszereket és a pontokat. A táblázatban található nyilak a gyakorlatban pointerekkel valósíthatók meg.

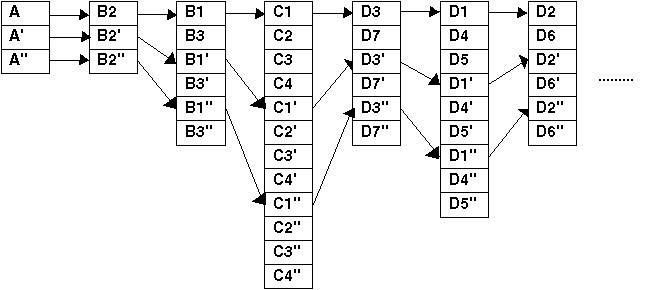
1.5 táblázat - hierarchikus észlelési rekord szórt tárolási struktúrában

A hálóstruktúrákat legcélszerűbben a rekordok közötti láncolás módszerével tárolhatjuk, illetve kereshetjük vissza.

Az 1.7 ábrán látható hálóstruktúra példánk egyirányú láncolást figyelembe véve az 1.16 ábrán látható módon szervezhető. Ha kétirányú láncolást végzünk, mely több előnnyel is rendelkezik, úgy a vizsgált struktúrát az 1.17 ábrán látható módon szervezhetjük meg.

1.16 ábra - hálós észlelési rekord egyirányú láncolásos tárolási struktúrában

1.17 ábra - hálós észlelési rekord kétirányú láncolásos tárolási struktúrában

Indexelt keresési eljárások

A címláncolásos keresési eljárásoknál a pointereket magukkal az adatokkal együtt tároltuk és csak a kezdőcímeket tároltuk külön file formájában. Az indexeléses eljárás lényege az, hogy az indexeket külön file-ban tároljuk és ez a file teremt összefüggést a keresett mennyiség és annak fizikai címe között, azaz a tulajdonképpeni keresést csak egy viszonylag kisméretű file-ban kell végrehajtani.

Megkülönböztetünk primer és szekunder indexelést, bár feladatainkat elsősorban szekunder indexeléssel oldjuk meg, a teljesség kedvéért röviden ismertetjük a primer indexelés lényegét is.

Primer indexelésnél a file rendezési fogalmához rendeltünk egy indextáblázatot (1.6 táblázat). Ez az indextáblázat tehát tartalmazza a rendezési fogalom növekvő értékeit és minden fogalomhoz hozzárendeli azt a rekordot (vagy annak a rekordnak a fizikai címét), amely a megadott rendezési fogalommal rendelkezik. A módszer alkalmazásának előnye lényegében abban rejlik, hogy az indexfile-ban a keresés direkt módszerrel hajtható végre, ugyanakkor, amikor a tulajdonképpeni adat-file tetszőleges módon, akár szekvenciálisan, akár szórtan, tárolható.

mezőérték (rendezési fogalom	rekord (relatív) címe
100	1
106	2
110	3
111	4
117	5
120	6
121	7
124	8
130	9
133	10

1.6 táblázat - primer indextáblázat

A szekunder indexelés során minden keresési argumentumként jelentkező mezőértékhez indextáblázatot rendelünk.

A geodéziai alappontok file-jának indextáblázatát készítettük el szekunder indexeléssel az 1.7 táblázatban, míg a személyi file költséghelyek és fizetések szerinti szekunder indexelését az 1.8 és 1.9 táblázatok tartalmazzák. A szekunder indexszel ellátott fil- okat általában invertált file-oknak nevezzük. Abban az esetben, ha egy file minden mezejéhez indextáblázatot rendelünk, úgy teljesen invertált file-ról beszélünk. Gyakran az indextáblázat igen nagy helyigényű. Ennek csökkentésére célszerűnek látszik az invertált filet leíró bináris mátrix

Ennek a mátrixnak az a lényege, hogy soraiban nem a kérdéses mezők címeit tartalmazza, ezek a címek ugyanis a fejlécben helyezkednek el. Az indexsorokban 0- ások és 1-esek vannak, annak megfelelően, hogy az adott mennyiség a fejlécben szereplő címen megjelenik-e vagy sem. Kézenfekvő, hogy ebben a tárolási módban annyi oszlopot kell alkalmaznunk, ahány mezőről az indexelt file-ban beszélhetünk. Ezeket a mezőket azonban a kérdéses helyeken elég 1 bittel jelölni. A vizsgálatok azt mutatják, hogy ez a tárolási mód igen gyakran gazdaságos.

tulajdonság	érték	rekord (relatív) cím
	gránitpillér	4010, 5012, 6013, 2010
állandósítás	betonpillér	5040, 6010, 9045, 9046
	vasbeton torony	1520, 2120
	vasasztal	1630, 1640
	x1=1000.00 x2=500.00; y1=500.00 y2= 0.00	5210
hely	x1=500,00 x2=0.00; y1=500.00 y2=0.00	6010
	x1=1000.00 x2=500.00; y1=1000.00 y2=500.00	1520
	x1=500.00 x2=0.00; y1=1000.00 y2=500.00	1640
	-20-tól -10 m-ig	9045, 2120
ellipszoid magassága a geoid felett	-10-től 0 m-ig	1640, 6010
	0 m-től 10 m-ig	1520

1.7 táblázat - geodéziai alappontok szekunder indextáblázata

mezőérték (költséghely)	rekord (relatív) cím
10	1, 3, 7
20	2, 6, 9
30	4, 5, 8, 10

1.8 táblázat - fizetési jegyzék költséghelyek szerinti szekunder indextáblázata

mező érték (fizetés)	rekord (relatív) cím
70400	6
80500	2
80700	7
120300	1
130400	10
140000	5
160000	4, 9
190000	3
240000	8