A GIS és a szakértői rendszerek.

Ebben a részben az általános bevezető után megismerkedünk

a szakértői rendszerek feladataival és összetevőivel, áttekintjük
a tudásbázis elemeit, tárgyaljuk
a következtetési mechanizmusokat, felvázoljuk
a tudás modellezésével kapcsolatos kérdéseket, befejezésül pedig
példát mutatunk be a tudásalapú rendszer és a GIS összekapcsolására vadkender ültetvények modellezésére.

A GIS grafikus és leíró adatokat tartalmazó adatbázis, mely a GIS funkciók felhasználásával képes az adatok transzformálására, szemléltetésére, szelektálására, összekapcsolására, elemzésére, végső soron bonyolult lekérdezések végrehajtására.

A GIS-től lényegében függetlenül is felmerült már a 80-as évek végén [1] az intelligens adatbázisok fogalma, lényegében olyan adatbázisokról van szó, melyek az SQL szakmai bővítéseire is választ tudnak adni az adatbázisban található adatok és szakmai tudás-együttesek alapján. Az előző mondat alapján világos, hogy az intelligens adatbázisok nem mások mint a szakértői rendszerek és az adatbázisok magas szintű integrációi. Kézenfekvő, hogy mivel az adatok és jelenségek közel 80%-a területfüggő, az intelligens adatbázisok első szintje a GIS révén valósul meg, hisz az SQL térbeli bővítése a GIS szoftverekben realizálódik. Ebből viszont az is következik, hogy az adatbázisok zömének magasabb inteligencia színtje a szakértői rendszerek és a GIS magasabb színtű integrációjának következménye.

Napjainkban, amint erre az ismertetendő esettanulmányból is következtethetünk, a működő rendszerek az integráció alacsonyabb szintjét reprezentálják. A szakértői rnódszerek és az objektum orientált programozás közti formális hasonlóságok azonban azt sejtetik, hogy az objektum orientált GIS rendszerek terjedésével a szakértői rendszerek és a GIS magas színtű integrációja is napirendre kerül.

A szakértői rendszerek feladata és összetevői

A szakértői rendszerek koncepciója a kémiai kutatással kapcsoltban jelent meg a 60-as években, konkréten a Dendral rendszer létrehozásakor, mely feladata a vegyi összetevők megállapítása volt a tömegspektrográf mérési eredményei alapján. Ellentétben a mesterséges intelligencia korábbi kutatási irányával ez a megközelítés nem általános szabályok és minták kutatását erőltette, hanem abból indult ki, hogy bizonyos szűkebb szakterületen a szakértői tudás kifejezhető úgynevezett ökölszabályok együttesével.

A szakértői rendszer ebben a felfogásban tehát nem más, mint egy programrendszer, melynek feladata egy szűkebb szakterület feladatainak megoldása a rendszerbe betáplált tudás alapján. A rendszer hasonlóan az élő szakértőhöz azok alapján a szabályok és tények alapján hoz döntést, amelyekkel rendelkezik.

A szakértői rendszerek fejlődése azután vált gyorssá, miután létrehozták a rendszerek burkait (shells), olyan fejlesztői környezeteket, melyekben a konkrét tudásbázis és következtető 'gép' létrehozása leegyszerűsödött.

A szakértői rendszer a kérdéses szűk szakterületre vonatkozó tudást rendszerint valódi (élő) szakértőktől szerzi. Ahhoz, hogy ez a tudás a program rendszer számára is értelmezhető legyen a rendszerint informatikus végzettségű rendszer fejlesztő kikérdezi a szakértőt és az interjúk alapján megtervezi és feltölti a tudásbázist és beprogramozza a következtető gépet. A feltöltés igen lassú folyamat, tapasztalt fejlesztők szerint gyakoriak az olyan napok, hogy egy-két szabálynál vagy állításnál többet nem lehet bevinni. A rendszer burkok annyiban könnyítik a feladatot, hogy a programozás komplex utasításcsoportokkal - makrókkal végezhető.

A szakértői rendszerek felhasználói felületén a megoldások mellett az indoklások is általában megjelennek, részben a felhasználó megnyugtatására, részben a könnyebb hibafeltárásra. A tanácsadó, konzultáló rendszerek esetén a döntési folyamatban az interaktivitás elkerülhetetlen.

Ha a rendszereket a GIS-el összefüggésben használjuk, úgy a szakértői rendszer a GIS-ből nyeri az adatokat, illetve az eredményeket a GIS-en keresztül mutatja be, ezért ebben az esetben elő/utó (front/end) szoftverként kell installálni. Az integráció fejlettebb szintjén a rendszer maga is a GIS szoftver része.

Míg a tudásbázis tartalma kifejezetten szűk szakterületre vonatkozik, addig a következtető gép a mesterséges gondolkozás általános szabályait követi. Ezért lehetséges kölönböző tudásbázisokat ugyanazzal a következtető géppel feldolgozni.

A tudásbázis elemei

A tudásbázist tények, szabályok, vagy keretek alkotják.
A tényeket állítások argumentumok és logikai értékek (igaz, hamis) alkotják. A megfelelő attribútumokkal kiegészített állítás a mondat. A változók lehetnek kötetlenek, vagy az összeillesztési folyamatban értékeket vehetnek fel, ezeket a kötött változókat attribútumnak nevezzük. Akkor beszélünk tényről, ha a mondathoz logikai értéket rendelünk. Lássunk néhány példát:

a geodézia a földtudomány része
'a tudomány' a földtudomány része
Bokros Lajos Magyarország pénzügyminisztere.

A három rövid példából sok következtetést tudunk levonni. Az első és utolsó állításunk tény, ha feltételezzük, hogy mind a kettőhöz igaz logikai értéket csatolunk. A példákból látjuk, hogy az állításokat aláhúzással jelöltük (a magyarban az állítmány segédigei részét jelen időben el szoktuk hagyni), a kötetlen változókat pedig idézőjellel. Ez utóbbi helyébe a következtetési folyamatban pld. behelyettesíthetjük a meteorológiát.

Azt is látjuk a felsorolt tényekből, hogy azok kifejezhetnek állandó viszonyokat (első példa) és ideiglenes jelenségeket (harmadik példa).

A tudásbázisba új tényeket az assert (állít) különleges predikátummal vihetünk be, míg a tények törlésére a retract (visszavon) állítás szolgál.

A tudásbázis rögzítésének másik fontos struktúráját a szabályok képezik. Ezeket úgy nyerjük az állításokból, ha kiegészítjük azokat az AND, OR, NOT, if...then logikai műveletekkel. Különösen az implikációt kifejező if...then párnak van nagy szerepe a szabályok létrehozásában.

Azokat a rendszereket, melyek a tudást a javaslati logika szabályai szerint if...then párokba szervezik 'produkciós' rendszereknek hívják. Lássunk néhány egyszerű példát és a homogén értelmezés kedvéért fordítsuk magyarra az implikációs kőtőszókat is:

Ha

                   hosszú ideig nézik a képernyőt

            Akkor

                     gyöngülhet a látás;

Ha

                    rizikó faktor van jelen

            Akkor

                    megbetegedés fordulhat elő.

Ha a tényeket és szabályokat kapcsolatba hozzuk egymással, úgy következtetéseket vonhatunk le, melyek tulajdonképpen új tények.

Tételezzük fel, hogy tudásbázisunkban az alábbi szabály található:

Ha

                     csökken a nemzeti jövedelem

                Akkor

                     romlik az életszínvonal;

ugyanakkor a tudásbázisba bevittük azt a tényt is, hogy

                     csökken a nemzeti jövedelem.

A szabályok és tények összehasonlítása alapján rendszerünk azt az új, közvetlenül nem betáplált tényt fogja hozzátenni a tudásbázishoz, hogy

                      romlik az életszínvonal.

A Ha A Akkor B típusú implikációk tehát azt jelentik, hogy ha A igaz akkor B is igaz, de ez nem jelenti azt, hogy ha A hamis akkor B is hamis.

Az implikációt megfogalmazhatjuk egyenes és fordított formában is. A Ha A Akkor B egyenes formájú implikáció már több példánkban szerepelt, a fordított forma: B Ha A.

A szabályokhoz megbízhatósági faktorokat is mellékelhetünk például

                 MF=30

                      esik az eső

Ha

                      felhők vannak az égen;

azt jelenti, hogy felhős égbolt esetén 30% a valószínűsége annak, hogy esni fog az eső.

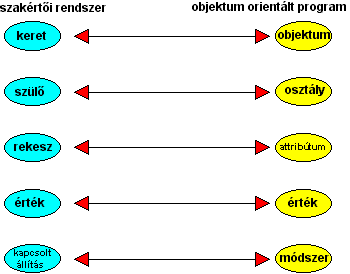
A keretek olyan struktúrák, melyek kombinálják a deklarációt és az eljárásokat a tudást leíró környezetben.

4.57 ábra - keretek és objektumok megfelelése

Tulajdonképpen tudáscsomagok létrehozására szolgálnak. A keretek funkcióik révén hasznosak a tudást képviselő rendszerek számára, s egyben befolyásolják a tudásbázist.

A keretek nagyon hasonlítanak az objektum orientált programozás objektum fogalmához.

A 4.57 ábrán felvázoltuk a két rendszer megfelelő fogalmait.

A kereteknek nevük van, pld. Nagy István, szülőjük, pld. személy, lehet egy sor rekeszük, mely értékeket vehet fel, példánk esetében egy rekesz lehet a kor, mely felveheti 19 év értéket.

Mivel az öröklődés a keret struktúráknak is része a keretek hálózatokba szervezhetők, melyek csomópontokból és kapcsolatokból állnak. Az öröklődési hierarchián kívül azonban a keretek szabályokhoz is kapcsolhatók, melyek lehetővé teszik az állítások aktivizálását a tudás tárolásakor és visszanyerésekor.

A keretek a struktúrában a fogalmak és dolgok deklarációját biztosítják, a keretekre hivatkozhatunk azok attribútumaival is az úgynevezett keret jegy kifejezéssel. A keret jegy leírására az alábbi formalizmust alkalmazhatjuk:

(keretreferencia attribútum(birtokos rag)),

ahol a keretreferencia egy keret neve vagy egy kert jegy, az attribútum pedig a kérdéses kerethez tartozó attribútum neve. Lássunk néhány példát. Deklaráljuk az alábbi két keretet:

      keret: Nagy Sándor

      szülő: diák

      attribútum: adjunktus

      attribútum: telefon érték: 463 2040

      keret: Siki Zoltán

      szülő: oktató

      attribútum: beosztás érték: adjunktus

      attribútum: tanszék érték: Általános Geodézia

      attribútum: hivatali helység érték: Kmf. 16 01

      attribútum: telefon érték: 463 1146

Nézzünk meg ezután hogy a fenti keretek ismeretében hogyan használhatjuk a keretjegyeket.
( Nagy Sándor telefon(ja)) megadja a 463 2040 telefon számot. De ha keretreferenciaként nem keretnevet hanem keret jegyet használunk úgy összekapcsolhatunk különböző objektumokat, például ((Nagy Sándor adjunktus(ának)) telefon(ja)) a 463 1146 értékel egyenlő, azaz a diák keretén keresztül eljutottunk az oktatója telefonszámáig. Ily módon a kiértékelés folyamatában lehetőségünk van az ilyen típusú keretjegyek felhasználásával hozzájutni az információhoz.

Természetesen szükségünk lehet olyan értékek adására is, melyeket a későbbiek folyamán vissza akarunk nyerni. Lényeges hogy a programnyelvekhez hasonlóan itt is megkülönböztessük az értékadást az összehasonlítástól. Míg az értékadásra := jelet használunk, addig az összehasonlításra a = jelet. Például a (Nagy Sánor telefon(ja))=463 2040 mondat értéke csak ebben az egy esetben igaz, ha a jobboldalra bármilyen más számot írunk a kifejezés értéke hamis lesz. Ha a (Nagy Sánor telefon(ja)):=463 3212 értékadó kifejezést írjuk fel ez azt jelenti, hogy átírtuk az eredeti keretet és ezentúl a kérdéses keret a következőképpen lesz tárolva:

      keret: Nagy Sándor

      szülő: diák

      attribútum: adjunktus

      attribútum: telefon érték: 463 3212

A kapcsolt állítások segítségével szabályokat kapcsolhatunk a keretek attribútumaihoz, ezek követik az információ tárolását és visszanyerését a keret rendszerben. A kapcsolt állításokon keresztül válik aktívvá a tudásbázis. Az adatok vagy tudás elérésekor a szabályok automatikusan beindulnak és különböző helyekre outputot eredményezhetnek.

A kapcsolt állítások realizálják a trigger elvet, ami azt jelenti hogy egy bizonyos akció mindenképpen végbemegy, ha a szükséges feltételek fennállnak.

A kapcsolt állításokat az attribútumokhoz kapcsolják 'ha szükséges' vagy 'ha bevisszük' formában. Például ha egy személyautó nevű keretben a fogyasztás nevű rekeszhez hozzákapcsolunk egy 'ha szükséges' állítást, úgy az abban az esetben, ha az attribútum értéke üres, de a következtetéshez szükséges megjelentet a képernyőn egy promptot, melyben kéri az attribútum érték (a fogyasztási adatok) bevitelét. Jelentős szerepük lehet a 'ha bevisszük' állításoknak az értékadások ellenőrzésében, vezérlésében.

Nem kívánunk itt részletesen szólni az objektum orientált programozással kapcsolatban már felvázolt öröklődésről. Csak arra szeretnénk felhívni a figyelmet, hogy ez az eszköz jelentős megtakarítást biztosít a tulajdonságok tárolásában, hisz a közös tulajdonságokat csak egyszer kell tárolni. Mivel a jelenségek általában könnyebben leírhatók hálós struktúrával mint tiszta hierarchiában a keret rendszerek megengedik a többszörös öröklődést s így egy-egy keret több szülőtől is örökölhet.

A következtetési mechanizmusok

A szabályok és tények kombinálását konklúziók levezetése érdekében következtetésnek hívjuk. A folyamatot grafikusan gyakran a lehetőségek fája segítségével ábrázoljuk. A fák csomópontjai a szabály-mondatok, a csomópontokat összekötő ágak pedig ezeket kapcsolják össze. Az összekapcsolás történhet logikai szorzással, ilyenkor ÉS csomópontról beszélünk és logikai összeadással, mely VAGY csomópontot eredményez.

A fa struktúra alkalmazásával sok esetben jól tudjuk modellezni a következtetés dinamizmusát a fa ágain történő haladás segítségével. ÉS csomópont esetén a csomópont alatti valamennyi feltételt meg kell vizsgálnunk, míg VAGY csomópont esetén elég az egyik alsó csomópont vizsgálata.

A fa gyökerében az az alapcél helyezkedik el melyet a következtetési folyamatban bizonyítani kívánunk. A bizonyításhoz bejárjuk a fentiek szerint a szükséges ÉS és VAGY csomópontokat. A bejárt csomópontok egymásutánja a bizonyítási út, mely nem más mint a főcél alatti fa egy része.

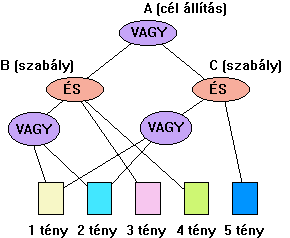
A fa bejárása különböző sorrendben történhet. A hátra láncolt következtetésnél a gyökérből indulunk ki és az ágakon keresztül jutunk el a levelekig, míg el nem érjük a tényeket. Az előre láncolt következtetésnél a levelekből indulunk ki és olyan utat keresünk mely az ágakon és csomópontokon keresztül a főcélhoz vezet. Lássuk az elmondottakat a 4.58 ábra egyszerű példáján.

4.58 ábra - következtetési fa

Hátra láncolás esetén vesszük az A gyökeret és megnézzük mi kell annak a bizonyításához, hogy A igaz. Látható, hogy ez akkor igazolható, ha vagy B vagy C igaz. Ha a B felé vizsgálódunk tovább (például azért mert C hamis) akkor D-nek és E-nek is igaznak kell lenie a bizonyításhoz. Az előre láncolt stratégia esetén D-ből és E-ből indolunk ki s ezek igazsága esetén B is igaz s ennek következményeképpen igazoltuk a főcél A igazságát.

Lássunk egy kissé konkrétabb példát a hátra láncolásos következtetésre.

Legyen a bizonyítandó állítás:

     A hallgató a geomatikai szakot választja (A).

A tudásbázisunkban szerepeljenek a következő tények:

     Az osztályfőnök a geomatikai szakot javasolja (1)

     Az osztályfőnök a villamos informatikai szakot javasolja (2)

     A matematika tanár a villamos informatikai szakot javasolja (3)

     A villamos informatikai szakon magas lesz a bekerülési pontszám (4)

     A geomatikai szakon alacsony lesz a bekerülési pontszám (5).

Rendelkezzen a rendszer az adatok mellett két szabállyal is:

            (B) szabály

                  A hallgató 'X'-t választja

ha

                  Az osztályfőnök 'X'-t javasolja

ÉS

                  A matematika tanár 'X'-t javasolja

ÉS

                  A bekerülési pontszám NEM magas lesz 'X'-ben

                 (C) szabály

                  A hallgató 'X'-t választja

ha

                  Az osztályfőnök 'X'-t javasolja

ÉS

                  A bekerülési pontszám alacsony lesz 'X'-ben

A 4.59 ábrán felvázoltuk a bemutatott példa tény és szabály rendszerét.
A hátra láncolásos következtetési mechanizmus első lépésben a következtető gép megnézi, hogy a hallgató a geomatikai szakot választja tartalmú A célállítás megtalálható-e ebben a formában a ténybázisban vagy a szabálygyűjteményben. Mivel nem, megnézi, hogy ha az 'X' kötetlen változó helyére behelyettesíti a célban szereplő értéket azaz a geomatikai szakot igaz állítást kap-e a B szabály feldolgozásával..

4.59 ábra - szakválasztási következtetési példa

Azt találja, hogy bár az 1 tény kielégíti a szabály első feltételét, a második feltétel már nem elégíthető ki, ezért vissza megy a gyökérbe és a VAGY feltétel figyelembe vételével megpróbálkozik a C szabály alkalmazásával. Ez a szabály kielégíthető 'X' igényelt behelyettesítésével, mivel így a szabály első feltétele azonos lesz az 1 ténnyel, második feltétele pedig az 5 ténnyel.

A fenti példában azt kívántuk megerősíteni hogy az általunk feltételezett állítás helyes. Mi történik azonban akkor ha a választott szakot valamely kötetlen változóval jelöljük, azaz ha nincs ötletünk a hallgató választására és azt szeretnénk megtudni, hogy a rendelkezésre álló tények és szabályok alapján mi lesz a hallgató választása.

Mivel a következtető gép az adatok között nem talál olyan állítást, mely tartalmazza az 'Y' kötetlen változót, megpróbálja az első szabályban 'X'-t 'Y'-hoz 'kötni', azaz 'X'-t 'Y'-al helyettesíteni. Ezután a szabály minden feltételét célként kezelve megpróbálja a ténybázis felhasználásával igazolni őket. Behelyettesíti tehát 'Y' helyére a geomatikai szakot (az 1 tényből) és megnézi, hogy a másik két feltétel is teljesül-e erre az attribútumra. A harmadik feltétel azonban az adatbázissal összehasonlítva hamis értéket ad ezért a következtetést korábbi helyre visszamenve új kapcsolat létrehozásával kell folytatni.
Ebből a visszalépésből ered tulajdonképpen a módszer elnevezése is. Másodszorra megpróbálja az első szabály kiértékelését az 'Y'-t a villamos informatika szakhoz kapcsolva, majd miután ez is hamis értéket ad megkezdi a második szabály vizsgálatát az elmondottakkal azonos módon és végül megadja a helyes eredményt.

Előre láncolt következtetések esetén a szabályok feltételeinek vizsgálatára koncentrál a kiértékelés, a levonható konklúziókat pedig hozzáadja a tudásbázishoz. A módszer alapelvét a kissé módosított előző példánk segítségével világíthatjuk meg. Legyen a tény bázisunk a következő:

      Az osztályfőnök a geomatikai szakot javasolja (1)

      Az osztályfőnök a villamos informatikai szakot javasolja (2)

      Az osztályfőnök a mérnök fizikusi szakot javasolja (3)

      A matematika tanár a villamos informatikai szakot javasolja (4)

      A matematika tanár a mérnök fizikusi szakot javasolja (5).

Határozzunk meg e mellett egy szabály együttest is ami nem más mint a szabályok egy részének csoportba foglalása.

 Első szabály:

ha

            az osztályfőnök 'X'-t javasol

ÉS

            a matematika tanár 'X'-t javasol

      akkor

            a diák 'X'-t választ;

Második szabály:

ha

            'X' 'Y'-t választ

      akkor

            'X' 'Y' tanulója lesz;

A következtető gép először az első szabályt fogja vizsgálni. Megnézi a ténybázis első tagját és azt találja, hogy 'X' a geomatikai szakhoz köthető. A szabály következő feltétele azonban már ezzel a kötéssel nem elégíthető ki ezért újra kezdi a szabály első feltételének a vizsgálatát a ténybázisból nyerhető következő kötéssel: 'X' kötődjön a villamos informatikai szakhoz. Ez a kapcsolat már kielégíti az első szabály mindkét feltételét, következésképpen az eredményt azaz hogy 'a diák villamos informatikai szakot választ' a rendszer beviszi a ténybázisba.

A következő lépésben a következtető gép a második szabályt értékeli ki, hozzákapcsolja az újonnan nyert tény alapján az 'X'-t a diákhoz az 'Y'-t a villamos informatikai szakhoz és a szabály konklúzióját miszerint a diák a villamos informatikai szak tanulója lesz beviszi a tudásbázisba.

Ezután a program visszatér az első szabály vizsgálatához és megpróbálja az 'X'-höz a mérnök fizikusi szakot kapcsolni. Ezzel a kötéssel az első szabály mindkét feltétele kielégíthető, a konklúziót pedig, hogy a diák mérnök fizikusi szakot választ beviszi a ténybázisba. Ezután sor kerül az új tény felhasználásával a második szabály aktivizálására és a konklúzió bevitelére a tudásbázisban. Mivel több sikeres kapcsolásra az első szabályban nincs lehetőség a folyamat befejeződik. Az eredményt esetünkben a következtetési folyamán nyert új tények reprezentálják.

Előre láncolt következtetések esetén is lehetséges hipotézis felállítása, mely lecsökkentheti az elemzés volumenét, e mellett különböző stratégiák is alkalmazhatók a szabályok végrehajtási sorrendjét illetően.
Példánkban mielőtt visszatértünk az első szabály vizsgálatához valamennyi szabályt megvizsgáltuk. Eljárhatunk azonban másképpen is, ha a következtetési mechanizmust három lépésre bontjuk:

Illesztés. Valamennyi szabályt összehasonlítjuk a ténybázissal és meghatározzuk a sikeres illeszkedéseket;
A konfliktus feloldása. Több illeszkedő szabály esetén egy, több vagy valamennyi szabályt kiválaszthatjuk a stratégia függvényében;
Végrehajtás. Hozzáadjuk a kiválasztott szabály(ok) következtetés(eit) a ténybázishoz.

Említsünk meg példaként néhány lehetséges stratégiát:

Válaszd az első illeszkedő szabályt;
Egyszerre add hozzá az összes konklúziót;
Dolgozz folyamatosan (ezt a stratégiát alkalmaztuk a példánkban);
Válaszd a kevéssé általános szabályt; Válaszd az újabb (később bevitt) ténnyel illeszkedő szabályt.

Az, hogy melyik az alkalmazandó stratégia a konkrét feladattól függ.
Sok esetben, különösen a térinformatikában, a szabályok és a tények nem kétszintűek az igaz vagy hamis érték szempontjából, hanem többszintűek, más szóval a rendelkezésünkre álló információ nem abszolút pontos. Ha a rendszerünkben ilyen tudásbázis van úgy a feladatok megoldását nem egzakt következtetéssel kell megoldani.

A következtetési mechanizmus alaptermészete ebben az esetben sem változik, más azonban az igaz értékek számításának és terjedésének módszere, valamint annyiban módosul a hátra láncolás mechanizmusa, hogy nem elégszünk meg a cél egyszeri bizonyításával, hisz arra is kíváncsiak vagyunk milyen a bizonyítás legnagyobb megbízhatósága ezt pedig csak akkor kapjuk meg, ha valamennyi lehetséges bizonyítást végigpróbálunk és képezzük ezek megbízhatóságának kombinációját.

A határozatlanság kifejezésére a szabályokat és tényeket megbízhatóság faktorokkal (MF) látjuk el. Az MF értékek 0 és 100 között változnak. Mivel a 0 a hamis értéknek 100 pedig az igaz értéknek felel meg az egzakt és nem egzakt tényeket és szabályokat kombinálhatjuk is a következtetési folyamatban.

A nem teljesen határozott rendszerek működése két részre osztható. Az első részben MF-eket rendelünk az elemi tényekhez és szabályokhoz. A második lépésben valamely következtetési mechanizmus és hibaterjedési modell segítségével meghatározzuk az összetett események MF-eit.

Ha a rendszer felépítése után a teszt futtatások nem járnak a kívánt eredménnyel három dolgot tehetünk:

megváltoztatjuk az elemi tudásbázis MF hozzárendeléseit;
megváltoztatunk néhány szabályt;
megváltoztatjuk a hibaterjedési elméletet.

Az első és második tényező megváltoztatása rendszerint visszacsatolás formájában részt vesz a következtetési folyamatban. A jól kiépített szakértői rendszerek e mellett lehetővé teszik, hogy a feladat megkezdése előtt, annak jellégétől függően beállítsák a hibaterjedési elméletet a rendelkezésre álló gyűjteményből (valószínűség elmélet, fuzzy logika, megbízhatóság elmélet, stb.).

Ahhoz, hogy a megbízhatóság terjedését követni tudjuk hátra láncolt következtetés esetén meg kell határoznunk az A és B állításokat tartalmazó alábbi kifejezések MF-eit:

            MF(nem A)

            MF(A és B)

            MF(A vagy B)

            MF(A,B) kombinációja.

A kombináció MF-jére azért van szükségünk, mivel ezzel számítható a cél megbízhatósága, ha két vagy több szabály is alátámasztja a hipotézisünket.
Amint már említettük szabályainkat különféle elméletek alapján is felírhatjuk, az alábbi szabályok a fuzzy logika törvényszerűségeit tükrözik [10].

MF(nem A) = 100-MF(A)                                  (35)

MF(A és B) = minimum[MF(A), MF(B)]                     (36)

MF(A vagy B) = maximum[MF(A), MF(B)]                   (37)

MF(A,B) kombinációja = MF(A) + MF(B) - [MF(A) * MF(B) / 100] (38).

Előfordulhat, hogy bizonyos esetekben semmilyen elképzelésünk sincs valamely tény vagy szabály megbízhatósági faktoráról. Ezekben az esetekben egy különleges igazság érték az ismeretlen használható.

Még egy terjedési szabályt szeretnénk bemutatni. Amint láttuk mind a szabályok, mind a tények korlátozott megbízhatóságúak. Mi lesz az új tény a következtetés megbízhatósága amelyet úgy nyerünk, hogy egy szabályba egy tényt (mindkettőnek van MF-je) helyettesítünk:

MF(következtetés) = MF(tény) * MF(szabály) / 100 (39).

A tudás modellezése.

Az előző alpont feltehetőleg meggyőzte az olvasót, hagy a szakértői rendszer tulajdonképpeni működése a következtetési mechanizmus még a legegyszerűbb példák esetén is bonyolultnak és hosszadalmasnak tűnik. Ahhoz, hogy rendszerünk sikeresen működjön mindenek előtt arra van szükségünk, hogy a jelenségeket a szűk feladat által megkövetelt szinten modellezzük.

A modellezés során mindenek előtt ki kell választanunk az objektumokat és a feladat által megkövetelt mélységig illetve szélességig le kell irnunk őket és kölcsönös kapcsolataikat. A fenti feladatot, felhasználva a keretek nyujtotta deklarációs és operációs lehetőségeket az alábbi csomópontok szerint kell elvégezni: elnevezés, jellemzés, szervezés, viszonyítás, korlátozás.

Az elnevezés, a keret neve egyedi kell, hogy legyen. A jellemzés részben az attribútumuk részben az öröklődés segítségével építhető fel. Ebből következik, hogy ha a szakértői rendszert keretformalizmussal készítjük különös figyelmet kell fordítanunk a hierarchiák felépítésére. Ezt a műveletet nevezzük szervezésnek. A keretek attribútumai más objektumok is lehetnek, ezen kívül a keretek szabályokhoz is kapcsolhatók. A korlátozások az attribútumokhoz kapcsolt állításokon keresztül valósítható meg.

Összefoglalva azt mondhatjuk, hogy a keretek szilárd alapot nyújtanak a tudás leképezésére és a következtetésre. A keret nevek biztosítják a címkéket, az attribútumok jellemzik és kapcsolják az objektumokat más objektumokhoz, a szülő-gyerek viszony deklarálása rendezi a tudást. A kapcsolatok attribútumok és szabályok segítségével is kifejezhetők. Az eredő tudásbázis korlátozása, a tárolási és visszanyerési folyamatok vezérlése a kapcsolt állításokkal realizálható. Hogy gyakorlatilag hogyan valósítható meg egy szakértői rendszer létrehozása azt jól illusztrálja az úgy nevezett tábla módszer.

A módszert egy beszédfelismerő rendszer kidolgozásával kapcsolatban alkalmazták először 1980-ban.
Több szakértőt hívtak meg a közös munkára, minden szakértő nagy szakértelemmel rendelkezett szűkebb szakterületén. A szakértők közvetlenül nem beszélgettek, de kapcsolatba léphettek egymással a koordinátoron keresztül, illetve olvashatták egymás ötleteit a tábláról.

A szakértőket egy szobába vezették, melyben egy nagy tábla volt, melyre a vendéglátók felírták a probléma kezdő állítását. Ezt elolvasva a szakértők elkezdtek gondolkozni. Amikor valamelyiknek egy jó ötlete támadt vagy egy érdekes hypotézist állított fel, kiment a táblához és felírta. A többiek ezt elolvasták és felhasználták az idegen területről származó tudást gondolataik továbbfejlesztésében. Végül az egyik szakértő megtalálta a megoldást és felírta a táblára.

A fenti bekezdésben foglaltak jól demonstrálják, hogy még szervezésileg sem könnyű különösen a tudományok határterületein az emberi tudás szűrt megszerzése, és még az is világos a leírásból, hogy értekezletek szervezésével nem lehet tudásbázist építeni.

Példa a tudásalapú rendszer és a GIS összekapcsolására vadkender ültetvények modellezésére [11].

A Georgia állam (USA) északi részén helyezkedik el a Chattahoochee Állami Erdőgazdaság. A vizsgált terület mintegy 1600 km² sűrű, aljnövényzettel gazdagon benőtt, erősen szabdalt területen elhelyezkedő erdő. A földrajzi viszonyok kedveznek a területen az illegális vadkender termelésnek egyrészt a vegetáció és éghajlat megfelelő e célra, másrészt az erdőgazdaság rendészete nehezen tudja rendszeresen bejárni az egész területet. A kendertermelő helyek felderítésére korábban légi fotogrammetriával próbálkoztak, ez azonban a mellett, hogy igen drága nem vezetett a kívánt eredményre mivel az erdő lombozata befedte a kritikus ültetvényeket.

A szakértői rendszer tudásbázisának feltöltése olyan rendész-ügynökök közreműködésével történt, akik nagy tapasztalattal rendelkeztek az ültetvények felkutatásában és likvidálásában. A tudás kódolását a 1stCLASS elnevezésű szakértői rendszer burok segítségével végezték. A tudásbázisba bevitt tényezők a következők voltak: domborzati viszonyok (lejtés és lejtő irány), úthálózattól mért távolság, vizektől mért távolság, lakott településektől mért távolság, erdő borítás jellemzői, a GIS adatbázis számára szükséges környezeti változók.

A GIS adatbázis létrehozásához a USGS (Egyesült Államok Geológiai Szolgálata) digitális 1:24000 méretarányú térképeinek síkrajzi-vízrajzi és DEM fedvényeit használták, valamint az erdészet tematikus fedvényeit. Ezekből az alapanyagokból az ARC/INFO GIS szoftver felhasználásával olyan új fedvényeket vezettek le melyek a tudásbázisba táplált tények és szabályok területi eloszlását reprezentálták (lejtés és lejtő irány, úthálózattól mért távolság, vizektől mért távolság, lakott településektől mért távolság).

A szakértői rendszer tudásbázisának és a GIS-nek az összekapcsolására interfész programot írtak C++ nyelven. A program négy fő modulból állt: interaktív adatbázis elérés, információ átvitel, döntés támogatás, megjelenítés. Az interfész legfontosabb feladata az volt, hogy a területet 200 m.* 200 m.-es hálóval borította, mely lehetővé tette az interaktívan kiválasztott négyzet önálló elemzését azaz a szakértői rendszer igénybevételét a célból hogy a vadkender termelés valószínűségét meghatározzák az adott négyzeten. E mellett a rendszer képes volt automatikus működésre is egy térképlap keretén belül, azaz grafikusan megjeleníteni a térképlapot lefedő hálót a hozzátartozó valószínűségekkel.

A rendszer célja az volt, hogy a bűnüldöző szervek ne üres kutatásokra fecséreljék idejüket, hanem akcióikkal a már valószínűsített helyeket célozzák meg.

Az elemzés után a végrehajtott akciók igazolták a rendszer javaslatait. A büntető akció során az ügynökök 90 termelő helyet azonosítottak s ebből 75 esett egybe a rendszer által megjósolttal, ami 83%-os eredményességnek felel meg.