GIS adatmodellek I

Ebben a részben először megismerkedünk a sok részre bontott negyedik fejezet

alapvető célkitűzéseivel, majd megkezdjük
az adatmodellek tárgyalását. Ezeken belül foglalkozunk

az elvi (koncepcionális) adatmodellekkel és
az implementációs modellekkel. Ezeken belül ismertetjük

a réteg szemléletű síkba feszítés fogalmát,
az objektum orientált módszert és
a függvénytér koncepcionális modell implementálását.

GIS adatmodellek és GIS műveletek

Az első fejezetben érintőlegesen foglalkoztunk az adatmodell fogalmával és viszonylag részletesen az alfanumerikus modelladatok adatbázisba szervezésével. A második fejezetben több helyen is tárgyaltuk a grafikus adatok modellezését, sőt utaltunk a Voronoi módszer kapcsán a leíró és geometriai adatok összekapcsolására is. Ugyancsak a második fejezetben a 3 dimenziós modellezéshez fűződően már szó volt egy bizonyos koncepcionális modellről és annak implementatív leképzéséről. A jelen fejezetben megpróbáljuk rendszerezni ezeket a kérdéseket, mivel e nélkül a különböző GIS műveletek nehezen értelmezhetők.

Tulajdonképpen magukat a műveleteket illetve azok elemeit is tárgyaltuk már mindhárom előző fejezetben e fejezetben megpróbáljuk rendszerezni eddigi ismereteinket és kiegészíteni néhány olyan fontos momentummal mint például a megjelenítés vagy a hálózatelemzés, melyekről eddig nem volt szó.

Az áttekinthetőség és viszonylagos teljesség érdekében mind a modellekről mind a műveletekről igyekszünk szoftver függetlenül szólni, ha mégis megemlítünk egy-egy szoftvert azt csak az illusztráció kedvéért tesszük. Fő feladatunk e fejezetben a funkcionalitás vizsgálata lesz, míg a 6. fejezetben e funkcionalitást fogjuk egyes kiválasztott programrendszerek műveleti sorára transzformálni.

Adatmodellek

Amikor adatmodellezésről szólunk azt a folyamatot próbáljuk körvonalazni, mely a valós világ tárgyait és folyamatait olymódon egyszerűsíti, hogy a rendelkezésre álló algoritmusok felhasználásával, a meglévő szoftver és hardver környezetben, földrajzi elemzésre, döntés előkészítésre és tervezésre alkalmasak legyenek. Mivel a tudomány és technika fejlődésével mind az algoritmikus mind a szoftver és hardver feltételek változnak a valóságot egyre jobban tükröző modellekkel dolgozhatunk. Nem igazán szerencsés ugyanakkor ha a fenti környezet minden elemének változása az egész modell, következésképpen valamennyi adat megváltozását vonja maga után.

Ezt elkerülendő, célszerű egy nagyon általános elvi (koncepcionális) adatmodell létrehozása, melyet különböző szinteken lehet még mindig logikai megvalósítási (implementációs) modellekben realizálni, az adott operációs rendszert és gépi környezetet figyelembe vevő fizikai modellek segítségével. Ez utóbbiak tárgyalása túlnő könyvünkön ezért csak utalások formájában lesz jelen a 6. fejezetben. A logikai modellek két hierarchia szintjével az alábbiakban foglalkozunk, de hivatkozunk a kérdésre a szabványosítással kapcsolatban az 5. fejezetben is.

Elvi (koncepcionális) adatmodellek

A GIS-ben általánosan használt koncepcionális adatmodell a valós világ entitásait (tárgyait) egyszerű objektumokba képezi le. Az egyszerű objektumok 2 dimenziós esetben olyan pontok, vonalak területek (poligonok), 3 dimenziós estben az előbbieken túl még felületek és testek, melyek tetszőleges számú konstans attribútummal (tulajdonságjellemzővel) rendelkeznek.

Ennek a megközelítésnek két hátránya azonnal szembetűnik. Gondoljunk arra, hogy egy várost szeretnénk egyszerű objektumként modellezni. A várost reprezentáló objektum ebben az esetben függ a felmérés illetve a megjelenítés méretarányától: kis méretarány esetén pont, nagyobb méretarány esetén pedig poligon. További probléma, hogy bár a városon belül még rengeteg objektum (pld. ház) van maga a modell nem rendeli a városhoz a házakat. Ezt a hozzárendelést csak kiegészítő attribútumok kézi vagy műveleti bevitelével érhetjük el. Nem kevesebb problémát jelent a foltszerű természeti objektumok leképezése e modellben. A konstans attribútum értékek megkövetelik, hogy a mért és általában hely és időfüggő attribútumokat e változásoktól eltekintve átlagoljuk és így tároljuk és analizáljuk.

A mesterséges objektumokkal kapcsolatban felvetett problémák lényegi része kiküszöbölhető, ha összetett objektum típusú koncepcionális adatmodellt alkalmazunk. Ebben az esetben, előbbi példánknál maradva, az összetett objektum a város, mely kerületekből áll, a kerületek háztömbökből, a tömbök házakból stb. Bármely hierarchia szintről eljuthatunk a magasabb és alacsonyabb szintekre. Természetesen problémák ebben a modellben is felléphetnek, gondoljunk például arra, hogy nem egyértelmű, vajon a városhoz vagy a főközlekedési úthoz tartozik-e az átvezető szakasz.

A természeti jelenségek függvény terekként foghatók fel. Bizonyos jelenségek viszonylag lassan változnak például a talaj vegyi összetétele, ezek 2 vagy 3 dimenziós skalár-terekkel írhatók le, más jelenségek pld. a meteorológiai frontok gyorsan változnak, ezek modellezésére vektor-tereket használhatunk. Kézenfekvő, hogy a természeti jelenségek általános koncepcionális modelljeként függvénytér típusú modellt, vagy valamely megközelítését kell alkalmaznunk.

Implementációs modellek

Az implementációs modelleknek nagyon sok hierarchia szintje van. A legmagasabb szinten a koncepcionális modell elemek elérése és műveletekbe történő aktivizálása szerepel. Eggyel alacsonyabb logikai szinten jelenik meg a grafikus és alfanumerikus adatok kapcsolata az adott implementációban. A további szintekről a grafikus adatmodellekről, a grafikus adatok esetleges külön tárolásáról illetve a relációs adatbázis kezelésről már viszonylag részletesen szóltunk a 2. illetve 1. fejezetben.

Az egyszerű objektum típusú elvi adatmodell implementációs modelljének felső színtjén két módszert is alkalmazhatunk: a réteg szemléletű síkba feszítést illetve az objektum orientált módszert.

Az összetett objektum tipusú elvi adatmodell implementációja több logikai szinten is legcélszerűbben az objektum orientált eljárással végezhető.

A függvényterek implementálására rendszerint hálós (térrács) vagy háromszög (tetraéder) megközelítést alkalmaznak, de találkozunk interpoláló függvények együtthatóinak tárolásával is.

A réteg szemléletű síkba feszítés

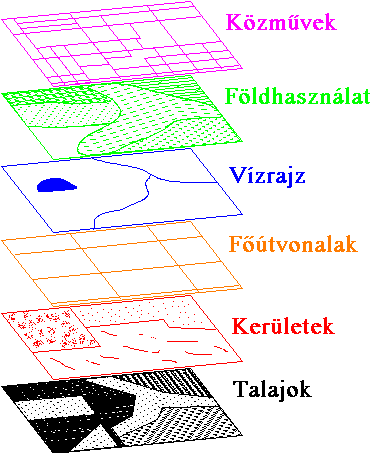
A módszer alapelvét a szemléletesség érdekében 2 dimenziós esetre vázoljuk fel. Bár elvileg elképzelhető a módszer alkalmazása 3 dimenziós esetben is a működő rendszerek túlnyomó többsége síkba transzformálja a valós világ jelenségeit. A modell lényege úgy foglalható össze, hogy a kérdéses munkaterületen kiválasztott egyszerű objektumokat olyan csoportokba szervezzük, melyek elemei nem fedik egymást s egyben szemantikai oldalról tekintve rokon tulajdonságokkal rendelkeznek. Egy ilyen csoportot nevezünk rétegnek vagy fedvénynek, a fogalom angol neve layer.

4.1 ábra - a terület rétegekre bontása

Kézenfekvő, hogy ennek a megszorításnak döntően a területi, esetleg a vonalas objektumok esetében van jelentősége.

A síkba feszítés fogalma azt jelenti, hogy az adott réteg objektumai kihagyás és átfedés nélkül, folyamatosan fedik le a síkot. Amint azt a 4.1 ábrán látjuk bizonyos egyszerű objektumok esetén például a talaj típusokat ábrázoló fedvényen a kihagyás nélküli takarás a telkek jellegéből következően automatikusan adódik, míg más jellegű fedvényeken mint például a vízrajz esetében a folyamatos takarás feltételét úgy biztosíthatjuk, ha feltételezzük, hogy minden olyan terület, melyet nem fednek le a vízrajzi elemek szintén alkot egy vagy több összefüggő objektumot, azaz az 'üres' területeket is objektumként kezeljük.
A logikai modell kizárólag azt a korlátozást írja elő a rétegek tartalmára vonatkozóan, hogy az egyes egyszerű objektumok egymást nem takarhatják.

Gyakorlati szempontból azonban nagyon fontos lehet a rétegek tematikus tartalmának gondos összeállítása, hisz a réteg orientált rendszerek csak az aktív réteg objektumait tudják elérni. Ha tehát például olyan kérdéseket teszünk fel a rendszernek, melyekre adandó válaszok különböző rétegekhez rendelt objektumokat érintenek, úgy vagy valamennyi érdekelt réteget külön-külön aktivizáljuk a lekérdezés idejére és az eredményt a kapott részválaszokból azok összesítésével állítjuk össze, vagy a meglévő rétegek felhasználásával új levezetett réteget kell létrehoznunk.

Szintén gyakorlati, hardver és szoftver specifikus megkötések fordulhatnak elő az egyes rétegek kiterjedésével kapcsolatban. A korszerű programrendszerek általában rugalmas kereteket biztosítanak az úgy nevezett 'projektek' definiálására. Egyes rendszereknél a projektek tárolási kategóriák, azaz már a betöltésnél korlátozva van az összetartozó rétegek kiterjedése. A fejlettebb rendszerek azonban nem élnek ilyen megkötésekkel és a felhasználó számára láthatatlanul végzik a szegmentálást. Az adatbázis aktivizálásakor azonban a rendszer fejlettségétől függetlenül célszerű a munkaterület lehatárolása mivel ezzel csökkenthető a betöltött adatok mennyisége s így gyorsítható a műveletek végrehajtása.

Egyes rendszerek a fentieken túl még olyan gyakorlati megkötésekkel is élnek, hogy a rétegek csak meghatározott objektum típust vagy típusokat tartalmazhatnak. Általában a terület típusú objektumokat tartalmazó rétegek nem tartalmazhatnak pont esetleg vonal típusú objektumokat.

Az objektum orientált módszer

Amint már említettük az objektum orientált módszer segítségével mind az egyszerű mind pedig az összetett objektum típusú koncepcionális modell implementálható. Különösen az összetett objektum típusú modell esetén mutatkoznak meg a módszer előnyei.

Az objektum orientált implementálás esetén nem kell a az objektumokat rétegekbe szervezni, ugyanakkor a rendszer lehetőséget nyújt hierarchikus halmazok kialakítására. A módszer alkalmazása esetén a munkaterületen (angol szóval region) található valamennyi objektum illetve objektum csoport közvetlenül érhető el és a rájuk illetve köztük deklarált műveletek elvégezhetők.

Az objektum orientált eljárás tulajdonképpen mint programozási elv jelent meg olyan programozási nyelvekben mint a Simula, C++, Flavors, Smalltalk-80, Eiffel, stb. A módszer teljes erejének kibontakozásához arra is szükség volt, hogy maga az adatbázis is objektum orientált elvek alapján szerveződjön. Az ezt a célt szolgáló fejlesztések olyan adatbázis-kezelő nyelvek és hátterükben álló adatbázis-kezelő rendszerek kialakulásához vezettek pint pld. a GemStone és a SIM. Már itt meg kell ugyanakkor jegyeznünk, hogy az objektum orientált adatbázis-kezelő rendszerekkel szerzett tapasztalatok még igen szerények a relációs adatbázis kezelő rendszerekkel összehasonlítva és ez az oka, hogy a nagy szoftver gyártók egyelőre még idegenkednek az új adatbázis típusra való átállástól. Ezzel magyarázható, hogy amint azt a későbbiekben látni fogjuk, még az objektum orientált GIS-ek is többnyire hagyományos adatbázisukban tárolják az adatokat.

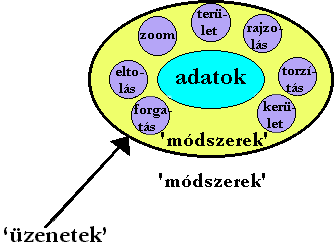
Az objektum orientált módszer (object oriented approach) négy alapvető tulajdonsággal rendelkezik.
Az első tulajdonság a 'becsomagolás' (encapsulation). Ez a fogalom azt jelenti, hogy a módszer az elemi objektumot akár csak az elemi objektumokból létrejövő csoportokat (részhalmazokat) és osztályokat (halmazokat) mint adatok és művelek együttesét definiálja. A 4.2 ábrán a becsomagolás eredményeképpen létrejövő objektum fogalmat illusztráltuk.

4.2 ábra - a 'becsomagolás' illusztrálása

A módszer sajátos szóhasználatában a műveletek illetve eljárások 'módszerek' (methods) nevet kaptak, míg a műveleteket kiváltó címzett utasításokat illetve eljárásokat 'üzeneteknek' (messages) hívják. Az üzenet megkeresi a címben szereplő objektumot mely módszerei a felkérés hatására működésbe lépnek és szükség esetén új üzenetet küldenek egy másik objektumhoz stb. A folyamat mindaddig folytatódik míg a komplex művelet végre nem hajtódott.

Mivel azonban valamennyi elemi objektum (instance) gyakran azonos módszerekkel történő becsomagolása fölöslegesen megduzzasztaná a programot az objektum orientált nyelvek a halmaz elméletből kölcsönzött absztrakt hierarhikus adattípusokba szervezik az elemi objektumokat. Ezek az együttesek: az osztály (class), csoportok (subclasses) és végül maguk az elemek (instances).

A objektum orientált módszer második alapelve az öröklődés (inheritance). Az öröklődés azt jelenti, hogy a magasabb hierarchia szinthez kapcsolt módszerek és adatok öröklődnek az alsóbb szinteken, hacsak valamely elemhez nem kapcsolunk egy azonos nevű módszert Ez utóbbi esetben ugyanis az elemhez címzett és a kérdéses magasabb szinten is definiált módszert kezdeményező üzenet hatására mindig az alacsonyabb szinten újradefiniált módszer lép akcióba. Az öröklődés nem csak egy 'őstől' de több őstől is lehetséges. Ez az úgy nevezett többszörös öröklődés.

A közös információ felhasználásának az öröklődéstől eltérő módszerét választották az úgy nevezett prototípus (prototype) rendszerek. Ezek a rendszerek nem különböztetik meg az osztályt és a az elemet, azaz nem alkalmazzák a hierarchiát. Bármely objektumot válszthatunk prototípusnak. Ha a kiválasztás megtörtént a többi objektumot összehasonlítjuk a kiválasztott prototípussal és az azonos tulajdonságaikat delegáljuk a prototípusban már tárolt tulajdonságokhoz, az eltérő tulajdonságokat pedig objektumonként tároljuk.

A hierarchikus és a prototípus szemlélet gondolati különbsége abban áll, hogy az előbbi előzetesen végzi el az absztrakciót az osztály hierarchia kialakításakor még az előtt, hogy az egyedi objektum elemek installálásra kerülnének, az utóbbi az installált konkrét objektumból kiindulva végzi a generalizálást meghatározva a közös illetve változó elemeket.

A vizsgálatok azt mutatják [1], hogy a prototípus rendszerek tár igénye kisebb futásideje viszont hosszabb mint a hierarchikus rendszereké. A legújabb kutatások szerint a prototipus elv összekapcsolva a hypergráf adatmodellel komoly lehetőségeket rejt magában a közmű hálózatok mint sokszorosan összetett objektumok implementációs modellezésében [2].

Harmadik alapelvként az objektum azonosságát (object identity) említjük. Ez a fogalom azt jelenti, hogy bármilyen transzformációnak is van az objektum alávetve, neve nem változhat meg.

Az utolsó alapelv a polimorfizmus (polymorphism), magyarra többalakúságnak fordíthatnánk, arra a hasznos tulajdonságra utal, hogy az objektum orientált rendszerben egy és ugyanaz az utasítás részleteiben különböző műveleteket eredményezhet attól függően, hogy melyik objektumnak címezzük. Ez a jellemző tulajdonképpen következménye a becsomagolásnak, mivel a konkrét műveletet (módszert) az objektum tartalmazza. Ha tehát például kiadjuk a draw utasítást és megcímezünk vele egy kört tároló objektumot, akkor az utasítás eredményeképpen egy kör jelenik meg képernyőn, ha azonban a cím egy tó határait tartalmazza, úgy ugyanazzal az utasítással a tó alaprajzát készítettük el. Nem igényel külön magyarázatot, hogy a polimorfizmus nagyon előnyös abból a szempontból, hogy az objektum megváltozása nem vonja maga után a program megváltoztatását.

Az objektum orientált módszer megjelenésekor a programozási munka egyszerűsítést, részekre bontását, rövidebb és áttekinthetőbb programok létrehozását tűzte ki céljául. A fejlődés azonban azt eredményezte, hogy e stílus lehetőségei meghaladták az eredeti célokat. E lehetőségek elsősorban az összetett adatstruktúrák modellezésében jelentkeznek. Azok az előnyök azonban melyeket az objektum orientált rendszer nyújt a rendszer konzisztenciája, egyszerű bővíthetősége, alkalmazásra alakíthatósága szempontjából akkor is indokolja alkalmazását, ha a rendszer koncepcionális adatmodelljét egyszerű objektumok alkotják.

A függvénytér koncepcionális modell implementálása

A függvényterek első, gyakorlatban is elterjedt implementációs modelljei a terepmagasságok modellezésével kapcsolatban alakultak ki. Két alapvető modell keletkezett: a négyzethálós, angol nevének rövidítésével DEM és a szórt pontokat Delaunay háromszögeléssel összekapcsoló TIN. Mindkét modellről már több helyen szóltunk itt csak azokra a jellemzőikre utalunk, melyek az implementációs logikai láncban jelentőséggel bírnak.

A gyakorlati implementálás során mind a két elrendezést rétegekben egyszerű, pont típusú objektumként tárolják. Az egyik különbség a két modell között abban áll, hogy rács esetén a modell elemeit a sarokpontok és lukbőség ismeretében a sor ás oszlop indexek egyértelműen pozícionálják, míg a szórt pontok esetében valamennyi vízszintes koordinátát tárolni kell. A másik különbség, hogy a rácspontok attribútumként csak a magasságokat tárolják, míg a szórt pontok a háromszögeket alkotó szomszédos pontok címeit is. Nem nehéz felfedezni, hogy milyen jelentős előnyökkel járna, ha ezeket a modelleket objektum orientált módon implementálnák.

A domborzatra kidolgozott modellek alkalmazhatóak volnának más kétdimenziós függvénytérre is pld. a talaj nedvesség tartalmára, csapadék eloszlásra, hőmérséklet eloszlásra, zaj terjedésre, talaj összetétel változásra, stb. A gyakorlatban azonban ezeket a jelenségeket igen gyakran az egyszerű, terület típusú objektumok segítségével modellezik, mely megközelítés természetesen sokkal durvább eredményeket szolgáltat.

Még kevesebb tapasztalattal rendelkezünk a három és négy dimenziós függvényterek implementációs modelljei vonatkozásában. Mindössze két olyan kereskedelmi szoftvert ismerünk, mely háromdimenziós jelenségek modellezését, megjelenítését és bizonyos mértékig elemzését tűzte ki céljául. A témára vonatkozó alapkutatások egyetemi műhelyekben folynak.

A modellezett jelenségek terei kölcsönhatásban állnak más olyan terekkel, melyek ugyanarra a tér (idő) tartományra vonatkoznak. Mind a modelleket, mind kölcsönhatásukat más terekkel elemezni, mérni és szemléltetni kell. A tartomány összes gyűjtött és modellezett adatát közösen kell tárolni és kezelni.

A hagyományos 2 D-s GIS arra képes, hogy felhasználva a topológiai strukturálás elvét (illetve valamely négyágú fa verziót a raszteres esetben) és a konstans attribútum fogalmat, azaz az egyszerű objektum típusú koncepcionális modellt, statikus objektumokat tároljon, kezeljen, elemezzen.

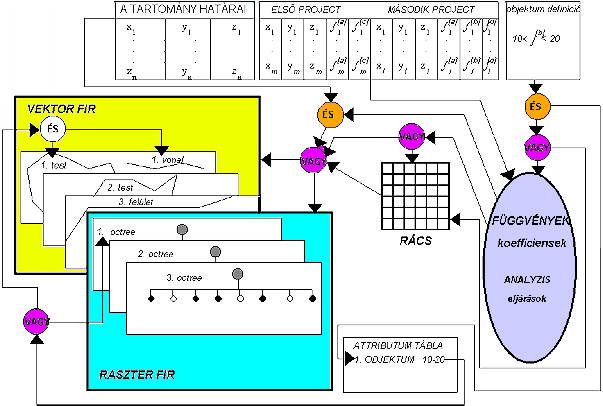
A 3 D-s GIS-nek megfelelő geometriai adat struktúrával kell rendelkeznie az előforduló 0, 1, 2, 3 dimenziós objektum típusok leírására de emellett még kiegészítő eszközei is kell hogy legyenek a változó attribútum értékek kezelésére. A 3 D-s modellezést támogató GIS környezet egy lehetséges realizálását a 4.3 ábrában vázoltam fel.

4.3 ábra - 3D-s modellezést támogató adatmodell

A koncepció legstatikusabb eleme a tartomány. Geometriailag a 2.49 ábrán bemutatott vektor eszközökkel vagy nyolcágú fával modellezhető. A tartomány attribútumai azok a terek, melyeket eredetileg a szórt mérési pontok reprezentáltak.

Az interpolációs eljárások vagy explicit függvények együtthatóivá, vagy szabályos rácsbeli értékekké transzformálják a szórt pontok adatait. Maguk az explicit függvények is felhasználhatók rácsadatok levezetésére, de valódi előnyük inkább az előzetes analízis végrehajtásában illetve a különböző kölcsönhatások számításában van. Az előzetes analízis például a szignifikáns gradiens változások detektálásával javíthatja a rácspontok levezetését.

Az objektumok ebben a sémában elvileg időleges képződmények, melyeket egy választott tulajdonságjellemző kijelölt értékintervallumára hoznak létre. A GIS szoftver támogatja a halmazműveleteket és a megjelenítési eljárásokat de a tárolás a függvény vagy rács struktúrán alapul.

Ez az általános struktúra egyszerűen lebontható több hagyományos (állandó attribútumokkal dolgozó) 3 D-s GIS-re kielégítve azon mérnöki szakterületek igényeit, melyek nem igénylik a magasabb felbontást illetve nem veszik figyelembe a jelenségek változó természetét.