3. Adatbázistervezés
3.1 Adatok közötti funkcionális kapcsolat
3.2. Adatok közötti többértékű függőség
3.3. Reláció kulcs fogalma
3.4. Redundancia fogalma
3.5 Redundancia megszüntetése, a relációk normál alakjai
3.5.1. Első normál forma (1NF)
3.5.2. Második normál forma (2NF)
3.5.3. Harmadik normál forma (3NF)
3.5.4. Boyce/Codd normál forma (BCNF)
3.5.5. Negyedik normál forma (4NF)
3.5.6. Ötödik normál forma (5NF)
3.6. Fizikai tervezés
3.6.1. Indexek fogalma és felépítése

3. Adatbázistervezés

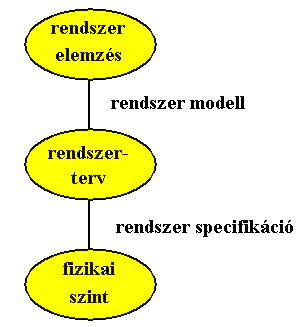
Az adatbázistervezés egy folyamat, mely több lépésből tevődik össze. Először az adatbázisban leképezendő rendszert elemzésnek vetjük alá és meghatározzuk a tárolandó adatok körét, azok egymásközötti kapcsolatait és az adatbázissal szemben felmerülő igényeket (fogalmi séma - Conceptual schema). Ezután következik a rendszer tervezés, melynek eredménye az adatbázis logikai modellje. Végül fizikai szinten képezzük le a logikai adatbázis modellt az alkalmazott szoftver és hardver függvényében.

3.1 ábra A tervezés lépései

A tényleges tervezés ismertetése előtt néhány újabb fogalmat kell bevezetni - funkcionális függőség, reláció kulcs, redundancia, - melyek segítségével a tervezés módszertana egyszerűbben magyarázható.

3.1 Adatok közötti funkcionális kapcsolat

Adatok között akkor áll fenn funkcionális kapcsolat, ha egy vagy több adat konkrét értékéből más adatok egyértelműen következnek. Például a személyi szám és a név között funkcionális kapcsolat áll fenn, mivel minden embernek különböző személyi száma van. Ezt a SZEMÉLYI_SZÁM -> NÉV kifejezéssel jelöljük vagy pedig egy diagrammal.

3.2 ábra Funkcionális függőség diagram

A funkcionális függőség bal oldalát a függőség meghatározójának nevezzük. A jobb oldalon levő egy, csak egy értéket határoz meg a funkcionális függőség. Nem áll fenn funkcionális függőség akkor, ha a meghatározó egy értékét több attribútum értékkel hozhatjuk kapcsolatba. Például a NÉV -> SZÜLETÉSI_ÉV állítás nem igaz, mert több személynek lehet azonos neve, akik különböző időpontokban születtek. Néhány évvel ezelőtt a SZEMÉLYI_SZÁM -> AUTÓ_TIPUS funkcionális függőség igaz volt, mert mindenkinek csak egy autója lehetett. Ma azonban ez már nem állja meg a helyét.

Az adatok közötti funkcionális függőségek az adatok természetéből következnek, nekünk csak fel kell ismerni ezeket a törvényszerűségeket. A tervezés során nagyon fontos, hogy ezeket pontosan felismerjük és figyelembe vegyük.

A funkcionális függőség jobb oldalán több attribútum is állhat. Például az AUTÓ_RENDSZÁM -> TIPUS, TULAJDONOS funkcionális függőség azt fejezi ki, hogy az autó rendszámából következik a típusa és a tulajdonos neve, mivel minden autónak különböző a rendszáma, minden autónak egy tulajdonosa és típusa van. Ezt diagrammal is ábrázolhatjuk.

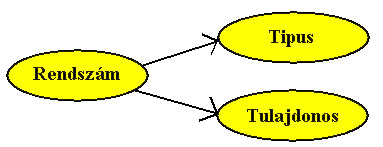
3.3 ábra Funkcionális függőség több meghatározott értékkel

Az is előfordulhat, hogy két attribútum kölcsönösen függ egymástól. Ez a helyzet például a házastársak esetén FÉRJ_SZEM_SZÁMA -> FELESÉG_SZEM_SZÁMA FELESÉG_SZEM_SZÉMA <- FÉRJ_SZEM_SZÁMA. Mindkét funkcionális kapcsolat igaz és ezt a FÉRJ_SZEM_SZÁMA <-> FELESÉG_SZEM_SZÁMA jelöléssel fejezzük ki. Természetesen a fenti összefüggés a többnejűséget megengedő országokban nem teljesül.

A funkcionális függőség bal oldalán több attribútum is megjelenhet, melyek együttesen határozzák meg a jobb oldalon szereplő attribútum értékét. Például hőmérsékletet mérünk különböző helyeken és időben úgy, hogy a helyszínek között azonosak is lehetnek. Ebben az esetben a következő funkcionális függőség áll fenn az attribútumok között:
HELY, IDŐPONT -> HŐMÉRSÉKLET. A fenti összefüggést az alábbi diagrammal is jelölhetjük:

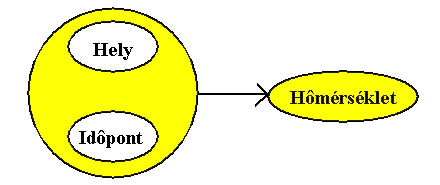
3.4 ábra Funkcionális függőség összetett meghatározóval

A funkcionális függőségek speciális esete a teljes funkcionális függőség. Erről akkor beszélhetünk, ha a meghatározó oldalon nincsen felesleges attribútum. Például a RENDSZÁM, TÍPUS -> SZÍN funkcionális függőség nem teljes funkcionális függőség, mivel a rendszám már egyértelműen meghatározza a kocsi színét, ehhez nincs szükség a típusra is.

A funkcionális függőség bevezetése után a relációk egy másik, matematikai jelölésekre épülő leírását is bemutatjuk. Általános formája:

reláció_név=({attribútumok},{funkcionális függőségek listája})

Például:

Az alábbi táblázat formában adott reláció

matematikai jelöléssel a következő formában
SZEMÉLYEK=({SZEMÉLYI_SZÁM, NÉV, MUNKAHELY}, {SZEMÉLYI_SZÁM -> NÉV,
SZEMÉLYI_SZÁM -> MUNKAHELY})
írható le a funkcionális függőségekkel együtt, feltételezve, hogy mindenkinek csak egy munkahelye van.

3.2 Adatok közötti többértékű függőség

Az adatok között fennálló kapcsolatok közül nem mindegyik fejezhető ki a funkcionális függőség segítségével. Például minden embernek lehet több szakmája, illetve ugyanazzal a szakmával több ember is rendelkezhet. Ebben az esetben egyik irányban sincs egyértelmű függőség. Ez egy többértékű függőség, az egyik attribútumhoz egy másik attribútum csoportja, halmaza kapcsolódik. A többértékű függőség ábrázolására a dupla nyilat használjuk. SZEMÉLYI_SZÁM ->> SZAKMA. A funkcionális függőséghez hasonlóan, többértékű függőség esetén is előfordulhat, hogy egy attribútum értékéből egynél több további attribútum értéke következik. Az előző példát bővítve: SZEMÉLYI_SZÁM ->> SZAKMA, OKLEVÉL_KELTE

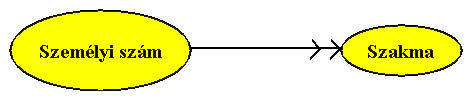
3.6 ábra Többértékű függőség diagram

A funkcionális és a többértékű függőség között kapcsolat van. Nagyon gyakran ugyanazt a függőségi kapcsolatot kifejezhetjük funkcionális és többértékű függőséggel is. Ennek bemutatására nézzük meg a következő példát.

Egy üzemben különböző termékeket gyártanak, melyek mindegyike többfajta alkatrészből tevődik össze. Szeretnénk nyilvántartani termékenként a felhasznált alkatrészek mennyiségét. Ezt leírhatjuk funkcionális függőség segítségével TERMÉK_AZONOSÍTÓ,ALKATRÉSZ_AZONOSÍTÓ -> MENNYISÉG, mely azt fejezi ki, hogy egy termékbe adott mennyiségű alkatrészt építettek be. Másik oldalról többértékű függőséggel is kifejezhetjük az adatok kapcsolatát. TERMÉK_AZONOSÍTÓ ->> ALKATRÉSZ_AZONOSÍTÓ, MENNYISÉG. Ez azt fejezi ki, hogy minden termékbe az alkatrészek egy csoportját és azoknak bizonyos mennyiségét építették be.

A funkcionális függőségeket mindig előnyben kell részesíteni a többértékű függőséggel szemben. Általános szabályként kimondhatjuk azt, hogy először az összes funkcionális függőséget írjuk fel, majd a hiányzó kapcsolatok leírására használjuk csak a többértékű függőséget.

3.3 Reláció kulcs fogalma

A reláció kulcs a reláció egy sorát azonosítja egyértelműen. A reláció - definíció szerint- nem tartalmazhat két azonos sort, ezért minden relációban létezik kulcs. A reláció kulcsnak a következő feltételeket kell teljesítenie

• az attribútumok egy olyan csoportja, melyek csak egy sort azonosítanak (egyértelműség)
• a kulcsban szereplő attribútumok egyetlen részhalmaza sem alkot kulcsot
• a kulcsban szereplő attribútumok értéke nem lehet definiálatlan (NULL)

A definiálatlan (NULL) értékek tárolását a relációs adatbázis kezelők speciálisan oldják meg. Numerikus értékek esetén a NULL érték és a 0 nem azonos.

Egy relációban tartsuk nyilván az osztály tanulóinak személyi adatait

3.7 ábra Reláció kulcs

SZEMÉLY_ADATOK=({ SZEMÉLYI_SZÁM, SZÜL_ÉV, NÉV}).
A SZEMÉLYI_ADATOK relációban a SZEMÉLYI_SZÁM attribútum kulcs, mert nem lehet az adatok között két különböző személy azonos személyi számmal. A születési év vagy a név nem azonosítja egyértelműen a reláció egy sorát mivel ugyanazon a napon is született tanulók vagy azonos nevűek is lehetnek az osztályban. Vajon a személyi szám és a születési év kulcsa-e a személyi adatok relációnak? Együtt a reláció egy sorát azonosítják, de nem tesznek eleget a kulcsokra vonatkozó azon feltételnek, hogy a bennük szereplő attribútumok részhalmaza nem lehet kulcs. Ebben az esetben a személyi szám már kulcs, így bármelyik másik attribútummal kombinálva már nem alkothat kulcsot.

Előfordulnak olyan relációk is, melyekben a kulcs több attribútum érték összekapcsolásával állítható elő. Készítsünk nyilvántartást a diákok különböző tantárgyakból szerzett osztályzatairól az alábbi relációval:
NAPLÓ=({SZEMÉLYI_SZÁM, TANTÁRGY, DÁTUM, OSZTÁLYZAT)}

3.8 ábra reláció összetett kulccsal

A NAPLÓ relációban a SZEMÉLYI_SZÁM nem azonosít egy sort, mivel egy diáknak több osztályzata is lehet akár ugyanabból a tantárgyból is. Ezért még a SZEMÉLYI_SZÁM és a TANTÁRGY sem alkot kulcsot. A SZEMÉLYI_SZÁM, TANTÁRGY és a DÁTUM is csak akkor alkot kulcsot, ha kizárjuk annak lehetőségét, hogy ugyanazon a napon ugyanabból a tantárgyból egy diák két osztályzatot kaphat. Abban az esetben, ha ez a feltételezés nem tartható (ennek a rendszer analiziséből kell kiderülnie!), akkor nem csak az osztályzat megszerzésének dátumát, hanem annak időpontját is tárolni kell. Ilyenkor természetesen a NAPLÓ relációt ezzel az új oszloppal ki kell bővíteni.

Nem csak összetett kulcsok fordulhatnak elő a relációkban, léteznek olyan relációk is, melyekben nem csak egy, hanem több kulcs is található. Ennek illusztrálására nézzük meg a következő relációt
KONZULTÁCIÓ=({TANÁR, IDŐPONT, DIÁK)}

3.9 ábra Reláció több kulccsal

A KONZULTÁCIÓ relációban a tanár illetve a diák oszlopban olyan azonosítót képzelünk, mely a személyt egyértelműen azonosítja (például személyi szám). Minden egyes diák több konzultáción vehet rész, minden tanár több konzultációt tarthat, sőt ugyanaz a diák ugyanannak a tanárnak más-más időpontokban tartott konzultációin is részt vehet. Ezekből következik, hogy sem a TANÁR, sem a DIÁK, sem pedig ez a két azonosító együtt nem kulcsa a relációnak. De egy személy egy időben csak egy helyen tartózkodhat. Ebből következik, hogy a TANÁR, IDŐPONT attribútumok kulcsot alkotnak, de ugyanilyen okból kifolyólag a DIÁK, IDŐPONT attribútumok is kulcsot alkotnak.

Vegyük észre azt, hogy a kulcsok nem önkényes döntések következtében alakulnak ki, hanem az adatok természetéből következnek, mint a funkcionális vagy a többértékű függőség.

A relációban külső kulcsot vagy kulcsokat is megkülönböztetünk. Ezek az attribútumok nem az adott relációban, hanem az adatbázis másik relációjában alkotnak kulcsot. Például ha a KONZULTÁCIÓ relációban a DIÁK azonosítására a személyi számot alkalmazzuk, akkor ez egy külső kulcs a személyi adatokat nyilvántartó relációhoz.

3.4 Redundancia fogalma

A logikai adatbázis tervezés egyik fő célja a redundanciák megszüntetése. Redundanciáról akkor beszélünk, ha valamely tényt vagy a többi adatból levezethető mennyiséget ismételten (többszörösen) tároljuk az adatbázisban. A redundancia, a szükségtelen tároló terület lefoglalása mellett, komplikált adatbázis frissítési és karbantartási műveletekhez vezet, melyek könnyen az adatbázis inkonzisztenciáját okozhatják. Egy adatbázis akkor inkonzisztens, ha egymásnak ellentmondó tényeket tartalmaz. Megjegyezzük, hogy a fizikai tervezés során az adatbázis műveletek gyorsítása érdekében esetleg redundáns attribútumokat is bevezetünk.

A redundancia egyik fajtája amikor ugyanazt a tényt többször tároljuk. Nézzük meg a következő relációt.

3.10 ábra Redundanciát tartalmazó reláció

A fenti relációban a tantárgyak össz óraszámát annyiszor tároljuk, ahány tanár tanítja az adott tantárgyat. A példa kedvéért feltételeztük, hogy egy tantárgyat több tanár is tanít. A redundancia a következő hátrányokkal jár:

• Ha egy tantárgy össz óraszáma megváltozik több helyen kell módosítani a relációban.
• Valahányszor egy új tanár kerül be a relációba ugyanannak a tantárgynak az előző soraiból kell elővenni az össz óraszám adatot.
• Az utolsó sorban szereplő tantárgy (angol) esetén még nem került kitöltésre a tanár személye. Új tanárnak a listára történő felvételekor ezt az esetet másként kell kezelni. Ilyenkor csak két üres értéket (tanár, tanított órák) kell átírni.

A redundanciát meg kell különböztetni az értékek duplikált (többszörös) tárolásától. A duplikált adattárolásra szükségünk lehet a relációkban, míg a redundanciát el kell kerülni. Vizsgáljuk meg a következő relációt.

3.11 ábra Adatok többszörös tárolása

Az előző táblázat a termék oszlopban többször tartalmazza a nyomtató és számítógép adatokat. Ez azonban nem okoz redundanciát, mivel egy termék több alkatrészből is állhat, így nem ugyanannak a ténynek a többszörös tárolásáról van szó, hanem egy másik tényt fejezünk ki, melyhez elengedhetetlen a duplikált tárolás. A duplikált és a redundáns adatok között a funkcionális függőségek vizsgálatával tehetünk különbséget. Ezt majd a normál formák ismertetésénél tesszük meg.

A redundancia fordul elő akkor is, ha levezett vagy levezethető mennyiségeket tárolunk a relációkban.

Levezetett adatokat tartalmazhat egyetlen reláció is abban az esetben, ha egyes attribútumok értéke egyértelműen meghatározható a többi attribútum alapján, például, ha a kerületet is nyilvántartjuk az irányítószám mellett. A redundáns adatok megszüntetésére két mód van. A levezetett adatokat tartalmazó relációkat vagy attribútumokat el kell hagyni. A relációkban tárolt redundáns tényeket a táblázatok szétbontásával, dekompozíciójával szüntethetjük meg (a 3.10 példában szereplő relációt kettő relációra bontjuk fel
Órák = {Tanár, Tantárgy, Tanított_Órák} és Össz_órák = {Tantárgy, Össz_óraszám}

3.5 Redundancia megszüntetése, a relációk normál alakjai

A logikai tervezés célja egy redundancia mentes reláció rendszer, relációs adatbázis. A reláció elmélet módszereket tartalmaz a redundancia megszüntetésére, az úgynevezett normál formák segítségével. A következőkben a relációk normál formáinak definícióját mutatjuk be példákon keresztül. A normál formák előállítása során a funkcionális és a többértékű függőség, valamint a reláció kulcs fogalmát használjuk fel. A normál formák képzése során leegyszerűsítve, olyan relációk felírása a cél, melyekben csak a reláció kulcsra vonatkozó tényeket tárolunk. Öt normál formát különböztetünk meg. A különböző normál formák egymásra épülnek, a második normál formában levő reláció első normál formában is van. A tervezés során a legmagasabb normál forma elérése a cél. Az első három normál forma a funkcionális függőségekben található redundanciák, míg a negyedik és ötödik a többértékű függőségekből adódó redundanciák megszüntetésére koncentrál.

A normál formákkal kapcsolatban két újabb a relációkhoz kapcsolódó fogalommal kell megismerkedni. Elsődleges attribútumnak nevezzük azokat az attribútumokat, melyek legalább egy reláció kulcsban szerepelnek. A többi attribútumot nem elsődlegesnek nevezzük.

3.5.1 Első normál forma (1NF)

Egy reláció első normál formában van, ha minden attribútuma egyszerű, nem összetett adat. A könyvben eddig szereplő valamennyi reláció kielégíti az első normál forma feltételét. Mintaképpen álljon itt egy olyan reláció, melynek attribútumai is relációk.

Szakkörök

Szakkör	Tanár	Diák	Osztály
Számítástechnika	Nagy Pál	Kiss Rita	III.b
Számítástechnika	Nagy Pál	Álmos Éva	II.c
Video	Gál János	Réz Ede	I.a
Video	Gál János	Vas Ferenc	II.b

3.13 ábra Nem normál formájú reláció és első normál formája

Annak eldöntése, hogy egy attribútumot egyszerűnek vagy összetettnek tekintünk nem mindig egyértelmű, az adatok felhasználásától is függ. A döntéseink során, hogy egy vagy több attribútumot tervezünk az adat tárolására, tartsuk szem előtt egyszerűbb több oszlopból egyet csinálni, mint egy oszlop tartalmát több részre vágni. Például egy vagy két attribútumban tároljuk a személyek vezeték és keresztnevét. Amennyiben a nevek között nem akarunk külön-külön kereszt és vezetéknév szerint keresni, akkor elfogadható lehet az egy mezőben tárolás.

3.5.2 Második normál forma (2NF)

Az első normál forma nem elegendő feltétel a redundanciák megszüntetésére. Egy reláció második normál alakjában nem tartalmazhat tényeket a reláció kulcs egy részére vonatkozóan. A második normál forma definíciója két feltétellel írható le.

• A reláció első normál formában van
• A reláció minden nem elsődleges attribútuma teljes funkcionális függőségben van az összes reláció kulccsal

Konferencia Terem Időpont Előadás B 10:00 Mitológia A 8:30 Irodalom B 11:30 Szinház A 11:00 Festészet A 13:15 Régészet

Termek Terem Férőhely A 130 B 250

3.14 Első normál formájú reláció és második normál alakú dekompozíciója

Az előző ábrán látható első reláció a következő matematikai formában írható le KONFERENCIA = ({TEREM, IDŐPONT, ELŐADÁS, FÉRŐHELY}, {TEREM, IDŐPONT-> ELŐADÁS, TEREM->FÉRŐHELY}). A reláció attribútumai között két funkcionális függőség adható meg, minden egyes teremben egyidőben csak egy előadás lehet és minden terem befogadóképessége adott. A reláció kulcsa a TEREM, IDŐPONT attribútumok, ezek a reláció elsődleges attribútumai. A másodlagos attribútumok (ELŐADÁS, FÉRŐHELY) közül a FÉRŐHELY csak a reláció kulcs egy részétől függ, ezért nincs második normál formában. A felbontás után keletkezett két reláció már második normál formában van. KONFERENCIA = ({TEREM, IDŐPONT, ELŐADÁS}, {TEREM, IDŐPONT-> ELŐADÁS}) TERMEK = (TEREM, FÉRŐHELY}, {TEREM-> FÉRŐHELY}). Minden nem elsődleges attribútum teljes funkcionális függőségben van a reláció kulccsal (TEREM, IDŐPONT illetve TEREM). Azok a relációk, melyek reláció kulcsa csak egy attribútumból áll, mindig második normál formában vannak, ekkor ugyanis nem lehetséges, hogy csak a reláció kulcs egy részétől függjön egy nem elsődleges attribútum.

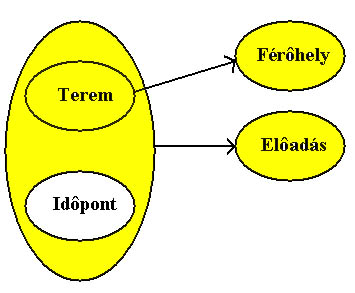
3.15 ábra Függőségi diagram

Nézzünk egy másik példát is a második normál forma feltételeit megsértő relációra. Egy épület energia gazdálkodásának ellenőrzésére az egyes helységekben rendszeresen megmérik a hőmérsékletet. A mérési eredmények értékeléséhez nyilvántartjuk az egyes helységekben található radiátorok számát is.

Konferencia Terem Időpont Hőmérséklet 213 98.11.18 23 213 98.11.24 22 213 98.12.05 21 214 98.12.05 21 214 98.12.15 20

Termek Terem Radiátor 213 2 214 3

A redundanciát ismét a táblázat két részre bontásával tudjuk megszüntetni.

További példa:
RAKTÁRI_NYILVÁNTARTÁS(alkatrész,raktár,mennyiség,raktár_cím)

3.5.3 Harmadik normál forma (3NF)

A második normál formájú relációkban nem lehetnek olyan tények, amelyek a reláció kulcs részeihez kapcsolódnak. Azonban ennek ellenére is lehet bennük redundancia, ha olyan tényeket tartalmaznak, amelyek a nem elsődleges attribútumokkal állnak kapcsolatban. Ezt a lehetőséget szünteti meg a harmadik normál forma. Egy reláció harmadik normál formában van, ha

• A reláció második normál formában van.
• A reláció nem tartalmaz funkcionális függőséget a nem elsődleges attribútumok között.

3.16 ábra Második normál formájú reláció és harmadik normál formájú dekompozíciója

3.17 ábra Függőségi diagram

A példában szereplő felső reláció második normál formában van, csak egy attribútumból áll a reláció kulcs és mindkét nem elsődleges attribútum teljes funkcionális függőségben van a reláció kulccsal. A reláció mégis tartalmaz redundanciát, mivel ugyanannak a tanárnak a születési éve többször is szerepel benne. A születési év funkcionálisan függ a tanár név attribútumtól. SZAKKÖRÖK = ({SZAKKÖR, TANÁR, SZÜLETÉSI ÉV}, {SZAKKÖR-> TANÁR, SZÜLETÉSI ÉV, TANÁR->SZÜLETÉSI ÉV}). A felbontás után a nem elsődleges attribútumok közötti függőséget kivettük az eredeti relációból: SZAKKÖRÖK = ({SZAKKÖR, TANÁR}, {SZAKKÖR->TANÁR}) TANÁROK = ({TANÁR, SZÜLETÉSI ÉV}, {TANÁR->SZÜLETÉSI ÉV}). Minden olyan reláció, mely második normál formában van és nincs vagy csak egy nem elsődleges attribútuma van, a harmadik normál forma feltételeit is kielégíti.

További példa:
SZEMÉLY_NYILVÁNTARTÁS(törzsszám,osztály,osztály_címe)

3.5.4 Boyce/Codd normál forma (BCNF)

A normál formák tárgyalása során eddig olyan relációkra mutattunk példákat, melyeknek csak egy reláció kulcsa van. A normál formák definíciója természetesen alkalmazható a több kulccsal rendelkező relációkra is. Ebben az esetben minden attribútum, mely valamely kulcsnak a része, elsődleges attribútum, de ez az attribútum függhet egy másik, ezt nem tartalmazó kulcs részétől. Ha ez a helyzet fennáll, redundanciát tartalmaz a reláció. Ennek a felismerése vezetett a harmadik normál forma egy szigorúbb definíciójához, a Boyce/Codd normál formához.

• A reláció harmadik normál formában van
• Minden elsődleges attribútum teljes funkcionális függőségben van azokkal a kulcsokkal, melyeknek nem része

Mintaként tekintsük a következő relációt:

Tantárgyak

Tanár	Időpont	Tantárgy	Félév	Diák_szám
Kiss Pál	93/1	Adatbázis	1	17
Jó Péter	93/1	Unix	1	21
Kiss Pál	93/2	Adatbázis	2	32
Jó Péter	93/1	Unix	2	19
KissPál	93/1	Adatbázis	3	25

Tantárgyak Időpont Tantárgy Félév Diák_szám 93/1 Adatbázis 1 17 93/1 Unix 1 21 93/2 Adatbázis 2 32 93/2 Unix 2 19 93/1 Adatbázis 3 25

Tanárok Tanár Időpont Tantárgy Kiss Pál 93/1 Adatbázis Jó Péter 93/1 Unix Kiss Pál 93/2 Adatbázis

3.18 ábra Reláció harmadik normál formája és Boyce/Codd normál formát kielégítő dekompozíciója

Tételezzük fel, hogy minden tanár csak egy tantárgyat, de annak különböző féléveit oktatja. Ezek alapján a következő funkcionális függőségek írhatók fel:

3.5.5 Negyedik normál forma (4NF)

Sajnos még a Boyce/Codd normál forma is tartalmazhat redundanciát. Mindeddig csak a funkcionális függőségeket vizsgáltuk, a többértékű függőségeket nem. A további két normál forma a többértékű függőségekből adódó redundancia kiszűrését szolgálja. Egy reláció negyedik normál formában van

• Harmadik normál formában van és
• egy X->>Y többértékű függőséget tartalmazó relációban csak az X és Y-ban megtalálható attribútumokat tartalmazza.

Képzeljük el azt, hogy egy relációban tároljuk a személyek, és barátaik nevét valamint hobbiját. Minden személynek több barátja és több hobbija is lehet.

Barátok-hobbik

Személy	Barát	Hobbi
Nagy József	Elek Attila	foci
Nagy József	Varga Attila	foci
Kiss Péter	Kiss Pál	sakk
Kiss Péter	Kiss Pál	video

Barát Személy Barát Nagy József Elek Attila Nagy József Varga Attila Kiss Péter Kiss Pál

Hobbi Személy Hobbi Nagy József foci Kiss Péter sakk Kiss Péter video

3.19 ábra Reláció és negyedik normál formája

Az eredeti reláció kulcsa valamennyi attribútumot tartalmazza. Csak egy kulcs van és nincsenek nem elsődleges attribútumok. Ezek alapján a reláció harmadik, sőt Boyce/Codd normál formában van, de mégis tartalmaz redundanciát, ugyanaz a személy-barát illetve személy-hobby kapcsolat többször is szerepelhet. A barát illetve hobby oszlop nem maradhat üres (NULL), mert része a kulcsnak! A reláció két többértékű függőséget tartalmaz: Személy->>Barát és Személy->>Hobbi. A negyedik normál forma szabályait kielégítő két relációra felbontva a redundancia megszüntethető.

További példa:
SZEMÉLYI_NYILVÁNTARTÁS(törzsszám,szakma,nyelv)

3.5.6. Ötödik normál forma (5NF)

Hosszú ideig a negyedik normál formát tartották a normalizálás utolsó lépésének. A többértékű függőségek külön relációkban tárolásával azonban információt veszthetünk. Ennek bemutatására nézzünk egy példát. Egy számítógépes ismeretek oktatására szakosodott Kft. több jól képzett tanárral rendelkezik. A tanárok többfajta tanfolyam oktatására is alkalmasak. A tanfolyamok az ország különböző részeiben kerülnek megtartásra. Ezek alapján állítsuk össze a Tanár-Tanfolyam-Helyszín relációt. Ebben a relációban csupán azt kívánjuk tárolni, hogy hol és milyen tanfolyamokat tartottak a tanárok, feltételezzük, hogy ugyanazon a helyszínen egyfajta tanfolyam csak egyszer kerül megtartásra.

Tanár-Tanfolyam-Helyszín

Tanár	Tanfolyam	Helyszín
Nagy Éva	Adatbázis I.	Szeged
Kiss Pál	Adatbázis I.	Győr
Nagy Éva	Adatbázis II.	Pécs
Kiss Pál	Adatbázis I.	Pécs

Tanár_Tanfolyam Tanár Tanfolyam Nagy Éva Adatbázis I. Kiss Pál Adatbázis I. Nagy Éva Adatbázis II.

Tanfolyam-Helyszín Tanfolyam Helyszín Adatbázis I. Szeged Adatbázis I. Győr Adatbázis II. Pécs Adatbázis I. Pécs

Tanár-Helyszín Tanár Helyszín Nagy Éva Szeged Kiss Pál Győr Nagy Éva Pécs Kiss Pál Pécs

3.20 ábra Reláció, dekompozíciója és ötödik normál formája

A következő függőségeket írhatjuk fel Tanár->>Tanfolyam Tanár->>Helyszín Tanfolyam->>Helyszín. Az egyetlen reláció kulcs tartalmazza az összes attribútumot (Tanár, Tanfolyam, Helyszín), ebből következik, hogy Boyce/Codd normál formában van a reláció, de mégis tartalmaz redundanciát. Például két sorban is megtalálható, hogy Kiss Pál Adatbázis I. tanfolyamot tanít. A relációt felbontva két - csak egy többértékű függőséget tartalmazó - relációra, (Tanár, Tanfolyam) és (Tanár, Helyszín), a redundancia megszüntetésével információt is vesztünk. A felbontás után már nem tudjuk, hogy a tanár melyik tantárgyát oktatja az adott helyszínen. Például Nagy Éva adatbázis I. vagy adatbázis II. tanfolyamot tart-e Pécsett. Az eredeti relációt három relációra felbontva kapjuk meg az ötödik normál formát. Az eredményül kapott három reláció összekapcsolásával előállítható az eredeti reláció, de bármelyik két reláció összekapcsolása még nem elegendő.

Az ötödik normál formának megfelelő felbontás eredményeképpen a tárolandó adatmennyiség megnövekszik, a reláció három táblára bontásával. Általában célszerűbb egy újabb oszlop bevezetésével csak két táblára bontani a relációt.

Tanfolyamok ID Tanfolyam Helyszín 1 Adatbázis I. Szeged 2 Adatbázis I. Győr 3 Adatbázis II. Pécs 4 Adatbázis I. Pécs

Tanfolyam_tanár Tanár ID Nagy Éva 1 Kiss Pál 2 Nagy Éva 3 Kiss Pál 4

Természetesen más felbontást is választhattunk volna, például a tanár-tanfolyam párokat is elláthattuk volna egy azonosítóval.

A normál formák tárgyalása végén megjegyezzük, hogy a harmadik normál formáig mindenféleképpen érdemes normalizálni a relációkat. Ez a redundanciák nagy részét kiszűri. Azok az esetek, melyekben a negyedik illetve az ötödik normál formák alkalmazására van szükség, ritkábban fordulnak elő. Az ötödik normál forma esetén a redundancia megszüntetése nagyobb tároló terület felhasználásával lehetséges csak. Így általában az adatbázis tervezője döntheti el, hogy az ötödik normál formát és a nagyobb adatbázist vagy a redundanciát és a komplikáltabb frissítési, módosítási algoritmusokat választja.

További példa:
FORGALMAZÁS(ügynök,cég,termék)

3.6. Fizikai tervezés

A relációs adatbázisok esetében a logikai tervezés során a relációk már elnyerhetik végleges alakjukat, melyeket egyszerűen leképezhetünk az adatbáziskezelőben. A fizikai tervezés során inkább arra koncentrálunk, hogy a logikai szerkezet mennyire felel meg a hatékony végrehajtás feltételeinek, illetve milyen indexeket rendeljünk az egyes relációkhoz. A relációkon végrehajtott művelet együttest tranzakciónak nevezzük és általában a tranzakciók gyors végrehajtását kívánjuk elérni.

A fizikai tervezés során előfordulhat, hogy a relációkba szándékosan redundanciákat építünk a hatékonyabb tranzakció kezelés érdekében. Ez visszalépésnek tünhet a logikai tervezés során követett következetes redundancia megszüntető tevékenységünkhöz képest. A lényeges különbség viszont az, hogy itt a redundancia ellenőrzött módon kerül be a relációba, nem csak véletlenül maradt ott a hiányos tervezés miatt. Gyakran előfordul például az, hogy a sűrűn együtt szükséges adatokat egy relációban tároljuk a lehető leggyorsabb visszakeresés érdekében.

3.6.1. Indexek fogalma és felépítése

A relációkban tárolt információk visszakeresését az indexek nagymértékben meggyorsíthatják, így a tervezés során nagy hangsúlyt kell fektetni a helyes indexek kiválasztására, szem előtt tartva azt is, hogy az indexek számának növelésével az adatok beviteléhez illetve módosításához szükséges idő megnövekszik az indexek frissítése miatt. A relációkhoz kapcsolt indexek segítségével az index kulcs ismeretében közvetlenül megkaphatjuk a kulcsot tartalmazó sor fizikai helyét az adatbázisban. Az indexek képzésére két módszer terjedt el, a hash kódok és a bináris fák.

A hash kódokat manapság már csak kevés adatbáziskezelő használja. Ennek a kódolási technikának az a lényege, hogy egy számítási algoritmus alapján magából az index kulcsból alakul ki a hash kód, mely alapján egy táblázatból kiolvasható a keresett értéket tartalmazó sor fizikai címe. A hash kód számítási algoritmusa nem mindig ad különböző értékeket az index kulcsokra. Ez abból is következik, hogy csak véges hosszúságú hash táblát tudunk kezelni. A hash kód ütközés kezelésére általában az azonos kódot adó kulcsokat összeláncolják egy listában. A láncok növekedésével természetesen a reláció sorainak eléréséhez szükséges idő is növekedik. A hash kód alapján történő visszakeresés nagyon hatékony. Sajnos azonban, több hátránya is van. A visszakeresés csak akkor lehetséges, ha a teljes index kulcs ismert. Az index kulcsnak egyben a reláció kulcsnak is kell lennie, hogy minél kevesebb ütközés legyen a hash táblában. Az index kulcs értékéből valamilyen matematikai művelettel képezik a hash kód értékét.

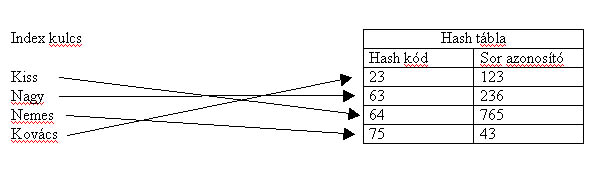
3.21 ábra Hash kódok

Ma már szinte kizárólag a bináris fákat alkalmazzák a relációs adatbázisokban. Ennél a módszernél a bináris keresést alkalmazzuk. Ehhez az index kulcsokat növekvő vagy csökkenő sorrendbe kell rendezni. A fa szerkezetet azért használják, mert nagy adatbázisok esetén az összes index kulcs nem tartható egyidőben a memóriában. A fa gyökere és csomópontjai nem tartalmazzák az index kulcshoz tartozó sor fizikai helyét, hanem csak a fa levelei. A keresés mindig a gyökértől kezdődik, a megfelelő ág felé folytatódik, és akkor ér véget, ha egy levélhez érünk. Ha a levélben tárolt index kulcs azonos a keresettel, akkor megtaláltuk a keresett értéket, ellenkező esetben sikertelen volt a keresés.

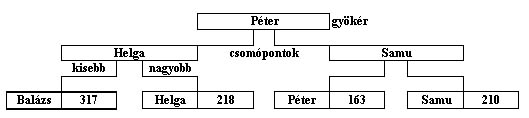
3.22 ábra Bináris fa index

A bináris fák felépítésénél arra törekszenek, hogy a fa valamennyi ága azonos hosszúságú legyen. Az ily módon felépített fát kiegyensúlyozott fának hívják. A kiegyensúlyozott fákban találhatjuk meg a lehető legkevesebb összehasonlítással a keresett elemet. A gyakorlati megoldásokban a hatékonyság kedvéért a csomópontokban nem csak egy index kulcs értéket tárolnak, hanem a háttértár tárolási egység (blokk) méretének megfelelő számút. A bináris fák segítségével egy konkrét index kulcsot vagy az index kulcsok egy tartományát kereshetjük meg. A reláció sorait az index kulcs szerinti növekvő vagy csökkenő sorrendben is végigjárhatjuk, ami a hash kód esetén nem lehetséges.

 

<<Elöző fejezet

Tartalom

Következő fejezet>>