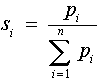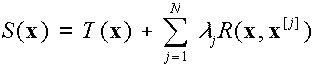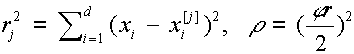Skalár terek modellezése

Ebben a részben megismerkedünk

1. a krigeléssel,
2. A skalár terek modellezésének általánosabb megközelítéseivel, ezen belül
1. a spline interpoláció néhány válfajával és
2. a skalár terek approximációjával a lokális modelleken alapúló becslés segítségével.

Eddigi 3 D-s modelljeinkben feltételeztük, hogy egy-egy test, egy-egy határokkal körülvett térbeli idom, egy-egy n dimenziós Voronoi (hiper)poliéder belseje homogén.

Ez a feltételezés bizonyos esetekben fizikailag is többé-kevésbé indokolt (pld. a barlangok esetében), más esetekben csak egy olyan viszonylag durva közelítés, mely a kisfelbontású globális modelleket kezelhetővé teszi. Úgy is tekinthetünk ezekre a modellekre mint a finomabb felbontású modell kiinduló pontjaira. Ha például az a feladatunk, hogy egy szénmezőben modellezzük a kénkoncentrációt, úgy először magát a szénmezőt mint homogén objektumot kell modelleznünk, majd ennek határain belül a finomabb változásokat.

A skalár terek modellezése bizonyos esetekben véglegesnek tekinthető eredményeket szolgáltat, bizonyos esetekben azonban csak az egy időpillanatra jellemző kiinduló helyzetet írja le. Az első eset akkor áll elő, ha statikus vagy lassan változó jelenségeket modellezünk, a második eset pedig dinamikusan változó jelenségek esetére jellemző. Ez utóbbi esetben tulajdonképpen vektor térrel modellezhetjük reálisan a jelenséget és skalár tér modellünk csak első megközelítésnek tekinthető.

Példaképpen a lassú változású terekre a Föld nehézségi erő potenciáltere szolgálhat, míg a gyorsan változó terekre példákat legkönnyebben az atmoszféra terei közül választhatunk (hőmérsékleti, légnyomási tér, stb.).

A skalár terek jellemző értékeit, különböző mintavételezési eljárásokkal határozhatjuk meg. A földalatti terekben rendszerint fúrásokkal nyerik az adatokat, míg az atmoszférában szondákkal esetleg helikopterekkel végzik a méréseket. Mind a földalatti mind a föld feletti mérésekre jellemző, hogy

• a mérések helyei gyakran jelentős hibákkal terheltek;
• a mért attribútum értékek megbízhatósága egyenetlen;
• a mérési helyek anyagi okokból igen ritkák;
• a mérési helyek az attribútum érték változásai szempontjából általában véletlenszerűek.

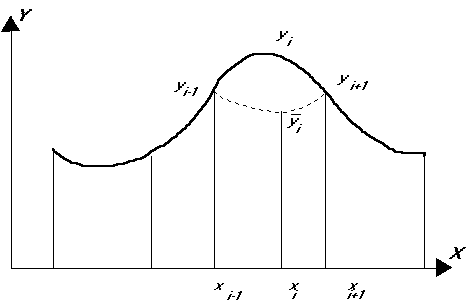
A negyedik sajátosság különleges jelentőséggel bír a megválasztandó interpolációs módszerek szempontjából. Közismert tény, hogy a súlyozott számtani közép képzés igen egyszerű s egyben megbízható módszer, amint erről az előző pontban a lopott területek módszere kapcsán már szóltunk. Annak a feltétele, hogy súlyozott középértékből megfelelő interpolációt végezhessünk az, hogy mérési pontjaink a függvény jellemző pontjaira essenek, meg tudjuk mérni a maximum és minimum helyeket a töréspontokat stb. A domborzat felmérése során a topográfus látja a terepet és éppen ezeken a pontokon határozza meg a magasságokat. Ezért lehetséges jó felmérés alapján jó minőségű digitális magasságmodellt interpolálni súlyozott számtani középképzéssel is. A skalár terek modellezésénél, amint már említettük, más a helyzet. Nem ismerjük a jellemző függvény értékeket, s ezért a mért értékek közepelésén alapuló módszerek nem szolgálhatnak kielégítő eredménnyel. Illusztráljuk az elmondottakat egy egyszerű egyváltozós függvénnyel (2.58 ábra).

2.58 ábra - a számtani közép nem mindig jó az interpolálásnál Véleményünk szerint a természeti folyamatokat leíró skalár terek inkább az utóbbi megközelítéssel koincidálnak.

Ha az xi pontban valamilyen átlagképzéssel interpolált függvény értéket -vel jelöljük, úgy az átlag képzési módjából következően , ha viszont egy polinómot illesztünk a mért pontokhoz, úgy azt kapjuk, hogy .

Néhány szó a krigelésről

A geostatisztikában általában, a bányászatban különösen, a feltalálójáról, Krige délafrikai professzorról krigelésnek nevezett súlyozott átlag képzésen alapuló módszert alkalmazzák az ismeretlen attribútum értékű pontok attribútum értékeinek meghatározására a más pontokban mért, azaz ismert, attribútum értékek alapján. A krigelés iránt behatóbban érdeklődők a módszer viszonylag részletes magyar nyelvű összefoglalását találhatják Steiner professzor A Geostatisztika Alapjai c. tankönyvében [20]. A jelen alpont csak a módszer rövid fölvázolására vállalkozhat elsősorban azzal a céllal, hogy az olvasó egybevethesse ezt az eljárást az interpoláció általunk javasolt megközelítésével.

A krigelés úgy kivánja meghatározni valamely geometriai pont ismeretlen attribútum értékét, hogy olyan súlyozott átlagot képez a más pontokban ismert (mért) attributum értékekből, mely szórása minimális.

Ahhoz, hogy az optimális súlyok meghatározhatók legyenek egy variogramm nevű görbe kiszámítása szükséges az ismert pontok koordinátáinak és attribútum értékeinek felhasználásával. Meghatározás szerint a variogramm

,

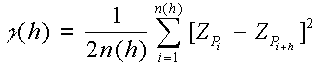ahol h a mért pontok közötti távolság, n(h) azoknak a mért pont pároknak a száma melyek egymástól h távolságra vannak, Z_Pi pedig a P_i pont attribútuma.

Anélkül, hogy belebonyolódnánk a részletekbe megjegyezzük, hogy a h távolság értelmezésében lehetőség van irányítottság figyelembe vételére is, azaz pld. kétdimenziós esetben, külön variogrammot készíthetünk Észak-Dél-i és Kelet-Nyugat-i értelmű h távolságokra. Ennek az eljárásnak akkor van értelme, ha az attribútum értékek távolság függése azimutálisan különböző.

Ha egy ponthalmazra elkészítjük a variogrammo(ka)t, úgy azt fogjuk látni, hogy egy bizonyos h távolságon túl a értékek már nem változnak tovább a h növekedésével. Azt a távolságot, ahol a variogramm növekedése megszünik hatástávolságnak nevezzük és H-al jelöljük.

A mért eredményekből szerkesztett variogramm nem sima függvény ezért a numerikus kezelhetőség megkivánja hogy valamilyen kiegyenlítési eljárással "sima" variogrammot számítsunk. Ehhez azonban az szükséges, hogy modellezzük valamely függvénnyel a variogramm elméleti alakját, mivel a kiegyenlítés csak a felvett függvény paramétereit szolgáltatja. Példaképpen [20] alapján a szférikus modellt mutatjuk be:

.

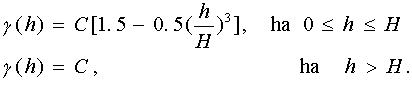A fenti kifejezésben a már ismert mennyiségeken kívül, C jelöli a variogramm maximális (telítettségi) értékét.

Amint azt a bevezetésben már említettük az ismeretlen P₀ pont keresett attribútum értékét Z(P₀)-t n darab közeli pont attribútumainak súlyozott középértékéből kívánjuk meghatározni.

Jelölje si az i.-ik súlyösszeggel normált pi súlyt (azaz

, ami azzal a haszonnal jár, hogy a figyelembe vett normált súlyok összege 1), akkor

.

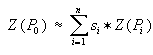A minimális szórású attribútum becslést szolgáltató normált súlyok az alábbi mátrix egyenletből határozhatók meg:

,

ahol , a K pedig az úgy nevezett Krige-mátrix:

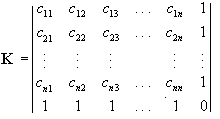
A súlyok kiszámításához tehát ismerni kell a K mátrix és a C₀ vektor elemeit. Ezeknek az elemeknek a meghatározásához volt tulajdonképpen szükségünk a simított variogrammra. A c_ij elemek ( esetben) a P_i és P_j pontok közötti h_ij távolság függvényében a variogrammból számolhatók mivel, , a diagonális elemek (c_ij az i=j esetben) pedig C-vel egyenlők. Az elmondottak érvényesek a c_0j típusú vektor elemekre is, ebben az esetben h_0j az ismeretlen attribútumú pont távolsága a j.-ik ismert attribútumú ponttól.

A fölvázolt algoritmus jól szemlélteti a krigelés népszerűségének a titkát - az egyszerűséget. Nem szabad azonban elfelejtenünk, hogy az egyszerűség egyből semmivé foszlik, ha anizotrópiát feltételezve próbáljuk végrehajtani a krigelést. Az anizotrópia feltételezése ugyanis azt jelenti, hogy a különböző irányokra más és más variogrammot kell szerkeszteni és K, valamint C₀ elemeit ezekből kell kiszámítani. Kézenfekvő, hogy az anizotrópia az eredeti krigelésben csak korlátozottan vehető figyelembe és így is csak akkor, ha mind az ismert mind az ismeretlen pontok valamilyen szabályos síkbeli vagy térbeli tesszellációban helyezkednek el.

A skalár terek modellezésének általánosabb megközelítése

A numerikus matematika tankönyveiben (lsd. pld [21]) három alapvető csoportba sorolják az interpolációs eljárásokat:

• polinómos interpolálás;
• trigonometriai függvényekkel történő interpolálás;
• exponenciális függvényekkel történő interpolálás.

A függvényekkel történő interpolálás azért csábító, mivel magában foglalja annak a lehetőségét, hogy viszonylag kevés paraméterrel írhatjuk le a szóban forgó jelenséget, s így jelentős tárolóhely megtakarítást érhetünk el. Sajnos a valós világ jelenségei a peremfeltételek összetettsége következtében gyakran torzult formában követik az alap törvényszerűségeket leíró függvényeket, ami azzal a következménnyel jár, hogy a kellő pontossággal közelítő függvénysorok tagszáma s egyben a tárolandó paraméterek száma jelentősen megnő. Nem szabad ugyanakkor elfelejtenünk, hogy a pontosság relatív fogalom, feladat és felbontás függő, s ezért eredeti elvárásunk a kis paraméterszám vonatkozásában sok esetben érvényre juthat. A függvényinterpoláció jelentősebb problémája az, hogy jelenség-függő, ami a gyakorlat nyelvére lefordítva azzal a következménnyel jár, hogy egy általános, függvényinterpoláción alapuló skalártér modellező szoftver szinte végtelen sok jelenség típusra felkészült szakértői rendszer létrehozását igényli, ami gyakorlatilag lehetetlen. Optimálisnak az általános modellezés megoldására az olyan hybrid interpolációs szoftver rendszer tűnik, mely a legfontosabb természeti jelenségeket függvényinterpolációval modellezi, ugyanakkor a függvényekkel nem kezelhető jelenségeket polinómos módszerrel közelíti.

Az első szélesen elterjedt 3 D-s modellező kereskedelmi program-csomag [15], mely a 2 D-s spline interpoláció 3 D-s kiterjesztését használja, Briggs 1973-ban kidolgozott eljárásán [22] alapul.

Az eredeti 2 D-s módszer az előre definiált rácspontokban határozza meg a függvényértékeket anélkül, hogy előbb meghatározná magát a térbeli változók folytonos függvényét, mely visszaadja a mért értékeket az adott helyzetű pontokon. A célból, hogy megküzdjön a két dimenziós polinóm szakaszok illesztési problémáival a szórt elhelyezkedésű észlelési pontokhoz, Briggs megoldotta a vékony lemez differenciál egyenletét, mely megoldás harmadrendű spline-hoz vezetett. A numerikus megoldásra differencia egyenletek szolgáltak, melyek megadták a függvényértékeket a szabályos rácspontokban. Az eljárás végtermékeként szintvonalas térképet állított elő; a szintvonalak és a rácsoldalak metszéspontjait négy pontos harmadfokú polinómmal interpolálta, e metszéspontokat pedig harmadfokú spline-al kötötte össze.

Sajnos a [15] nem tartalmaz semmi részletet a dimenzió kiterjesztés problémáiról, ennek ellenére valószínűsíthető, hogy a differencia egyenletek levezetése a 3 D-s esetben is a közelítő összgörbület négyzetének minimalizálásán alapul.

Mitašova és Mitaš [23], [24] kidolgozták a variációs feltételek explicit megoldását az első-, és másodfokú deriváltak direkt becslésével két, három és négy dimenziós esetekre. A kapott függvény, melyet az összes deriváltat tartalmazó u.n. 'simasági' funkcionál négyzetének minimalizálásával vezettek le az alábbi alakkal rendelkezik:

,

ahol a j index a mért pontokat,

az ismeretlen együtthatókat, R(x, x^[j]) pedig a bázisfüggvényeket jelöli.

A vizsgált esetekre T(x) = a₁ = constans. Három és négy dimenziós esetekben a bázis függvények az alábbiak:

^,

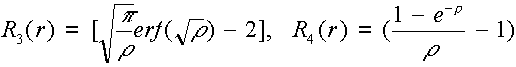ahol

,

pedig egy tetszőlegesen választott 'feszültségnek' nevezett paraméter, mely

szabályozza a rendszer hajlékonyságát,
a hibafüggvény.

A , a₁ összesen N+1 ismeretlen paramétert az alábbi N+1 lineáris egyenletből határozhatjuk meg, amelyekben z^[i]-el jelöljük az x^[i] pontban mért értéket;

.

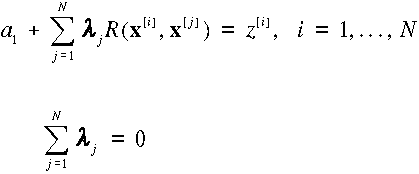Az explicit módszerrel kapcsolatban több kérdés vár további vizsgálatra.

Mindenek előtt az általános globális módszerek gyakorlati alkalmazása tűnik problematikusnak a nagy futási idő igény miatt, mely nagyságrendje egyébként a mért mennyiségek számának köbével arányosan növekszik.

A [23]-ben a szerzők olyan szegmentált eljárásra tesznek javaslatot, melyben számos átfedő lokális modellel közelítik a globális modellt. Sajnos a hivatkozott műben nem találunk utalást arra, hogy mennyiben függ a közelítés pontossága az átfedés mértékétől, a vizsgált jelenség sajátosságaitól stb. Ha azonban a módszert GIS függvényként kívánjuk alkalmazni úgy ki kell dolgozni az adott tűrések függvényében automatikusan szegmentáló eljárást is.

Ismeretesek olyan klasszikus szegmentáló eljárások is, melyek globális megoldáshoz vezetnek. Ha az elemzés azt mutatja, hogy lokális szegmentálással nem lehet kielégíteni a pontossági követelményeket, úgy alkalmazhatók a globális szegmenteló eljárások, lehetőleg kihasználva a párhuzamos feldolgozás előnyeit.

A modellezett három és négy dimenziós mezők megjelenítésére olyan program modulokat használtak, melyek lazán kapcsolódtak a GRASS GIS program legújabb verziójához. A laza kapcsolatot az indokolta, hogy a kérdéses GIS szoftver nem rendelkezik a megkívánt térbeli adatstruktúrákkal [24]. Ez a tény ismételten aláhúzza olyan nyílt GIS szoftver létrehozásának szükségességét, mely rendelkezik kiterjeszthető adatstruktúrákkal.

A krigelésnél bemutatott lineáris egyenlet rendszer legalább is külsőleg nagyon hasonlít a fenti rendszerre. Érdekes volna numerikus esetleg analitikus vizsgálatokat végezni a két rendszer lényegi viszonyát illetően.

A térbeli modellek analízise, különböző térmodellek egymásrahatása, a vizsgált jelenségek megjelenítése gyakran igényli a kérdéses attribútum értékek rácspontokban történő megjelenítését. Míg függvényinterpoláció esetén a rácspontokra levezetett mennyiségek csak közbenső értékek, addig polynómos interpoláció esetén a rácspontok egyben tárolási struktúrát is jelenthetnek, ugyanis a rácspontok tárolása mind műveleti mind tárolási oldalról gazdaságosabbnak mutatkozhat az összes polinóm együttható tárolásánál és a rácspont értékek sorozatos kiszámításánál.

Felmérve a polinómos interpoláció különleges szerepét a skalár terek modellezésében az Országos Tudományos Kutatási Alap 685 sz. kutatási témája keretében az alábbiakban ismertetendő polinómos skalár tér interpolációs módszert dolgozta ki Gáspár Péter tudományos munkatárs és a szerző [25].

Skalár terek approximációja a lokális modelleken alapuló becslés segítségével

Legyenek adva az f(r) térbeli skalár függvény u_i értékei az r_i pontokban (i=1,...,M). Feladatunk az f(r) függvényértékek közelítő meghatározása a nem mért r pontokban.

Minden ismert u_i értékű r_i pontban képezhetünk egy G_i(r) approximáló függvényt, mely jól közelíti az eredeti függvényt a pont közelében. A függvény legyen értelmezve az egész globális modellen és legalább a szomszédos pontokban adjon jó közelítést.

Egy tetszőleges r pontban valamennyi u_i,r=G_i(r), (i=1,...,M) lokális modellből számíthatunk közelítő értéket. Az u_i,r értékek különböző mértékben közelítik f(r) értékét. A közelítés pontossága attól függ, hogy milyen távol van az r pont a G_i(r) központi r_i pontjától.

Az u_i,r értékeket úgy tekinthetjük mint az f(r) függvény becsléseit a G_i lokális modellek által amiből következik, hogy az u_i,r értékek valószínűségi változók. E változók eloszlása ismeretlen, de néhány statisztikai jellemzőjük (például a szórásuk) becsülhető. A szórás becslésére az r_j ponton fellépő

eltérések szolgálnak. Ha ismerjük az M számú u_i,r érték valószínűségi jellemzőit, úgy belőlük f(r) várható értéke becsülhető. A legegyszerűbb becslési módszer a súlyozott számtani közép alkalmazása esetén

,

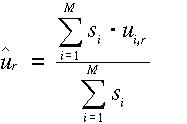ahol az s_i súlyok a szórásokból számolhatók az alábbiak szerint:

.

Természetesen a bemutatott becslés helyett más típusú becslés például a robosztus becslés is alkalmazható.

Lokális modellalkotás
A lokális modellek létrehozása a függvényapproximáció szokásos módszereivel történhet. Legegyszerűbb eljárásként a három ismeretlenes polinómokat alkalmazhatjuk az alábbiak szerint:

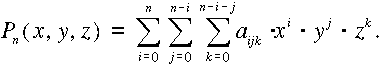
A gyakorlati igényeket a harmadfokú polinómok rendszerint kielégítik. Húsz együtthatójuk kiszámításához legalább ugyanennyi ismert ponttal kell rendelkeznünk.

Amikor az r_i környezetét közelítő G_i(r) függvény együtthatóit határozzuk meg az ismert pontokat ugyanebből a környezetből kell választanunk. A választás alapjául egy referencia távolság vagy koordináta különbség szolgálhat. Sokkal megbízhatóbb eredményt nyujt, ha a kérdéses pontokat a VORONOI poliéderek által nyújtott elsődleges és másodlagos szomszédságból választjuk.

Annak ellenére, hogy rendszerint simító módszereket használunk az együtthatók meghatározására megkívánhatjuk az u_i=G_i(r_i) feltétel teljesülését is az r_i pontban. G_i együtthatóit általában valamiféle kiegyenlítéssel, rendszerint a legkisebb négyzetek módszere felhasználásával számoljuk. E számításokban súlyokat is alkalmazhatunk az r_i-től mért távolság függvényében.

A lokálisan approximált G_i(r) függvény jól közelíti az f(r) függvényt a felhasznált ismert pontok tartományán belül. Az extrapolációs tartományban azonban a polinómos közelítés hibája rohamosan nő és a végtelen felé tart.

A szórások és súlyok számítása
A G_i(r) függvények létrehozása után kiszámíthatók a fluktuációk és a hozzájuk tartozó d_ij távolságok. Ha szakaszokra osztjuk a legnagyobb távolságot úgy az alábbiak szerint becsülhetjük meg egy kiválasztott szakasz átlagos távolságához tartozó szórásnégyzetet:

,

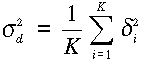ahol K a vizsgált intervallumba eső távolságok száma. Ha felrakjuk a d, s_d² érték párokat, úgy egy kiegyenlítő egyenes segítségével megkaphatjuk a G_i(r) függvényekkel becsült u_i,r értékek átlagos szórásnégyzetét a távolság függvényében.

Általánosságban a s_d²(d) függvény jól becsülhető az alábbi kifejezéssel:

,

ahol a függvény szórása az ismert pontokban, az a,b,c paraméterek pedig a d, s_d² értékpárokból számíthatók. Ha korábbi elképzelésünknek megfelelően előírjuk, hogy az r_i pontban G_i(r) = u_i , úgy c = 0.

Bizonyos esetekben előfordul, hogy a szórás irányfüggő. Ebben az esetben az euklideszi távolság helyett a következő távolságfogalmat használhatjuk:

.

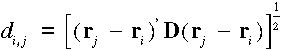Ebben az esetben a D mátrix elemeit a többi paraméterrel együtt kell meghatározni. Most már eltekinthetünk a szakaszokra bontástól és megbecsülhetjük a d_ij=d_ji szakaszokhoz tartozó és fluktuációkat, melyek felhasználásával

.

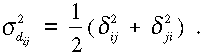Ha az r_i pontok térbeli eloszlása túlságosan egyenlőtlen úgy a globális függvény helyett külön szórás függvényt alkalmazhatunk minden lokális modellhez.

A szórásokból a súlyok az alábbiak szerint számíthatók:

.

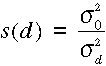A globális modell összeállítása
A lokális modellek alapján a tér valamennyi r pontjában kiszámíthatjuk a különböző u_i,r értékeket és meghatározhatjuk szórásaikat és súlyaikat. Az u_i,r; s_i,r , (i=1,2,...,M) (sorozat elemei úgy tekinthetők, mint az f(r) mennyiség meghatározására irányuló különböző pontosságú közvetett mérések. Következésképpen az várható értéket és szórását valamely paraméter becslési eljárással határozhatjuk meg. Az u_i,r mennyiségek korreláltsága általában elhanyagolható. A legegyszerűbb becslési eljárás a legkisebb négyzetek módszerének alkalmazásából következő súlyozott számtani közép:

.

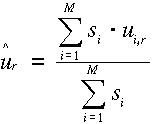A módszer hatékonysága növelhető, ha bevezetünk egy T hatástávolságot, melynél távolabbi pontokra konstruált G_i függvények nem szólnak bele a várható érték képzésbe.

A módszer nyujtotta f_M(r) globális approximálo függvény folyamatos és törésmentes az egész értelmezési tartományban, második deriváltjai szintén folyamatosak, maga a függvény pedig kellőképpen sima.

· az interpolálási téma keretében megismerkedhet a mesterséges neurális hálózatokkal

· esetleg visszatérhet az előző részhez

· illetve a tartalomjegyzékhez

---

Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc

---