Néhány kvázi szabványos illetve szabványos információtechnológiai eszköz II
Ezen a lapon
- a STEP szabvánnyal és
- az EXPRESS nyelvvel fogunk megismerkedni.
A STEP (Standard for Exchange of Product Model Data) azaz Termékmodell Adatok Csereszabványa nemzetközi szabvány (ISO 10303), mely eredetileg, mint különböző nemzeti javaslatok nemzetközi összegzése 1983-ban keletkezett. ISO szabvánnyá azonban csak 1994-ben vált. Ez a szabvány azonban tulajdonképpen csak egy ‘Alkalmazási Jegyzőkönyvet’ tartalmazott (AP-203), azaz hasonlóan az SDTS profiljaihoz, ez a szabvány is folyamatosan fejlődik új alkalmazási jegyzőkönyvek létrehozásával.
Mielőtt nagyon röviden felvázolnánk e szabvány struktúráját el kell mondanunk, hogy egyáltalán miért térünk ki rá tárgyalásunkban.
A szabvány adatmodelljének leírására konstruált EXPRESS információ modellező nyelvet ugyanis éppen a magyar térbeli adatátviteli szabvány alkalmazza. Ha tehát nem csak külföldi adatátviteli szabványokat akarunk ismertetni, hanem a hazait is fel akarjuk vázolni, akkor kell, hogy némi fogalommal rendelkezzünk az EXPRESS nyelvről. Ez viszont feltételezi, hogy ha csak nagy vonásokban is, vannak elképzeléseink a nyelv származásáról.
A STEP azt a célt tűzte ki, hogy a termék teljes életciklusára szabványosítsa a kapcsolódó információkat a célból, hogy azok kicserélhetők és megoszthatók legyenek, azaz a szabványos termékadatbázisok átvihetők legyenek más termékadatbázisokba, illetve a termékadatbázisokat egyszerre több felhasználó használhassa.
A termék alatt tulajdonképpen valamennyi mérnöki szakterület termékeit értik a gépektől a hajókon át az erőművekig, az épületekig és építészeti együttesekig, stb.
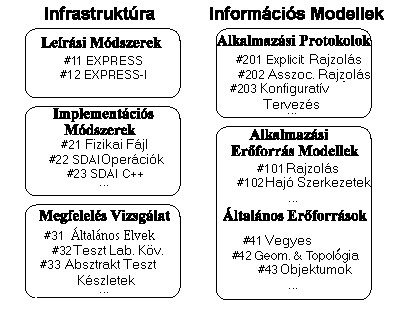
Ahhoz, hogy a szabvány már nyílt (félig kész) formájában is alkalmazható legyen két részre kellett osztani: infrastruktúrára és adatmodellekre, ahogyan ez az 5.55 és 5.56 ábrákon látható.
Az infrastruktúra, mely a leíró nyelvet, a fizikai implementálást és az általános ellenőrzési alapelveket (azaz, hogy miként lehet ellenőrizni, hogy valamilyen szoftver termék által lefordított EXPRESS állomány megőrizte e az eredeti modellt) tartalmazza nagy vonásokban már befejezett, míg az információs modellek tovább bővíthetőek. Ez utóbbiak az alábbi bontásban szerepelnek a szabványban: alkalmazási jegyzőkönyvek, alkalmazási modell erőforrások és általános erőforrások. Ez utóbbiak között szerepel a geometria és topológia is (mégpedig mind 2, mind pedig 3 D-s variánsban), ami megmagyarázza, hogy miért használható az EXPRESS nyelv térbeli adatátvitelre, hisz ezeket a modelleket a nyelv segítségével írja le a szabvány.
Az ipar specifikus részekből már készek az alkalmazási jegyzőkönyvek a gépészeti és villamosmérnöki területen és készítés alatt állnak az összetett anyagok, fémlemez kockák, autótervezés és gyártás, hajóépítés, erőművek, technológiai üzemek és más ágazatok számára. Idővel minden iparág ki fogja fejleszteni a saját alkalmazási jegyzőkönyvét.
A szakemberek szerint a szabvány használata még jelenlegi félig kész állapotában is nagy előnyökkel rendelkezik a DXF vagy IGES átviteli szabványokkal szemben a háromdimenziós test modellek átvitelében.
|
|
5.55 ábra - a STEP főbb alkotói |
5.56 ábra - STEP infrastruktúra és adatmodellek |
A STEP szabvány működése, nagyon vázlatosan, a következőképpen képzelhető el: EXPRESS nyelven definiálják a rajzolásra és tervezésre vonatkozó általános és konkrét információs modelleket és ezek szükséges részeinek felhasználásával kialakítják a kérdéses szakterületet érintő Alkalmazási Jegyzőkönyvet. Attól függően, hogy a kérdéses erőforrás mennyire általános több vagy kevesebb A J-ben vesz részt. Míg az általános erőforrások minden alkalmazást támogatnak a specifikusabb erőforrások csak néhány A J-t, melyek adatainak és módszereinek együttdolgozása indokolt.
Az EXPRESS-ben megírt elvont modellek az EXPRESS-I nyelv specifikációinak felhasználásával konkrét adatokkal tölthetők meg, mely adatok az úgy nevezett Tiszta Szöveg Kódolással (2.1 rész) ASCII fájlként implementálhatók. Az implementációs módszerek a fenti kódoláson túl specifikálják a szabványos adatelérési interfészt, a C++, C, FORTRAN, IDL és JAVA nyelvekhez való kötést (interfészelést) is.
Gondoskodik a szabvány a specifikációit realizáló szoftverek tesztelési módszereiről is.
Az EXPRESS nyelv
A már említett EXPRESS és EXPRESS I nyelv grafikus ábrázolására szolgál az EXPRESS G nyelv. E mellett még említést érdemelnek az EXPRESS V és továbbfejlesztése az EXPRESS X nyelv, mely rendeltetése, hogy biztosítsa a leképezéseket az EXPRESS-ben definiált információ modellek között, illetve tegye lehetővé az EXPRESS és más modellek és alkalmazások (pld. IGES) közötti leképezéseket.
Az EXPRESS nyelv objektum orientált absztrakt modellező nyelv, mely leírja a valós világ választott nézetének objektum csoportjait, objektumait, azok tulajdonságait, egymással kialakított kapcsolatait (relációit), az objektumokra és kapcsolataikra jellemző korlátozásokat. Amint már említettük, az EXPRESS-ben definiált objektumokhoz és jellemzőikhez adat jellegű értékeket az EXPRESS I nyelv specifikációi alapján rendelhetünk.
Mielőtt hozzákezdenénk a nyelv rendszeresebb megismeréséhez, lássuk hogy miként deklarálhatjuk a derékszögű koordinátákkal jellemzett (Descartes-i) pontot (bár a bevezetés kedvéért magyar objektum és attribútum neveket használunk valódi feladatoknál ezt nem érdemes megcsinálni, mivel így elveszítjük az előredefiniált modulok felhasználásának lehetőségét, mivel ezekben a modulokban minden angolul van írva, ezért néhány példánkban a nevek is angolok lesznek nem csak a kulcsszavak):
ENTITY descartesi_pont;
SUBTYPE OF (pont);
koordinatak : LIST [1:3] OF hossz_mertek;
END_ENTITY;
Amint látjuk a derékszögű koordinátákkal jellemzett pontot jellemzi, hogy az objektum egy altípusa az általános pont objektumnak, attribútumai a koordináták, melyek egy három hosszúság értéket tartalmazó listán helyezkednek el.
Lássuk ezek után az EXPRESS legfontosabb alkotóelemeit:
- SCHEMA - valamilyen mértékben kapcsolódó információ összefogó kerete, magyarul sémának nevezhetjük;
- ENTITY - az objektum meghatározása;
- ATTRIBUTE - attribútum, az objektum tulajdonság jellemzője;
- TYPE - típus, a felvehető értéktartomány jellemzője;
- RULE - szabály, mely kezeli a teljes vagy részleges korlátozásokat;
- CONSTANT - konstans;
- FUNCTION - függvény;
- PROCEDURE - eljárás;
- STATEMENT - végrehajtódó utasítás.
Bár mint látjuk programozási eszközök is találhatók a nyelvben, az EXPRESS nem programozási, hanem leíró, modellező nyelv.
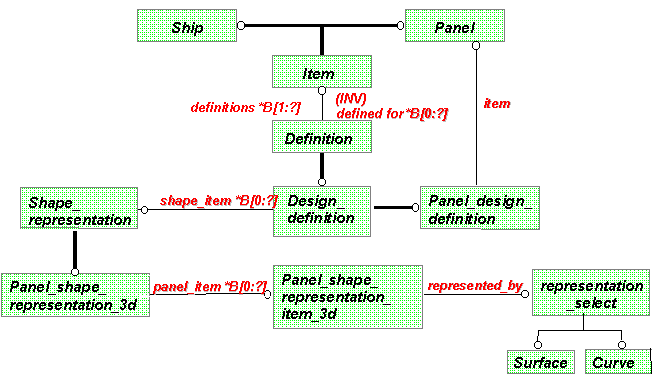
Ezután ugorjunk bele a mély vízbe és lássunk egy első látásra bonyolultnak tűnő hajóépítési példát, melyet az EPM Technology cég Internetről letölthető Power Point bemutatójából kölcsönöztünk, illetve kisebb javításokkal láttunk el. Meg kell jegyeznünk, hogy színeket csak a könnyebb áttekinthetőség kedvéért alkalmaztunk, illetve hogy ennél az első példánál nem fordítottuk ékezetes betűk nélküli magyarra az objektumokat és attribútumokat, amint azt néhány további példánkban elkövettük (5.57 ábra).
Egyelőre a nélkül, hogy a nyelvi formalizmusokba belemennénk próbáljuk megérteni a példaként szolgáló modellt.
Az elem (Item) objektum a hajó (Ship) objektum és a panel (Panel) objektum generalizálása - szuper típusa, míg ez utóbbiak az Item altípusai. A panel tervezési definíció (Panel_design_definition) nevű objektum elem (item) attribútumán keresztül kapcsolatban van a panel objektummal (ez utóbbi határozza meg az elem értéktartományát, azaz típusát). A kérdéses elem meghatározásának (Definition) a tervezési definíció (Design_definition) altípusa, mely objektum pedig a panel tervezési definíció (Panel_design_definition) objektum szuper típusa. A meghatározás (Definition) objektum a meghatározások (definitions) halmaz típusú attribútummal kapcsolódik az elem (Item) objektumhoz (a halmaz összetevői elem típusúak). |
|
A tervezési definíció (Design_definition) objektum az elem alak (shape_item) attribútum halmazzal kapcsolódik az alak reprezentáció (Shape_representation) objektumhoz (a halmaz összetevői ilyen típusúak), mely szuper típusa a panel három dimenziós reprezentációja (Panel_shape_representation_3d) objektumnak.
Ez utóbbi objektum a panel elem (panel_item) attribútumokkal kapcsolódik a panel 3D-s reprezentációs elem (Panel_shape_representation_item_3d) objektumhoz, mely reprezentálva által (represented_by) attribútumának értéktartománya a reprezentációt választ (representation_select) objektumban van. Ez az objektum a megjelenítést a kapott attribútum információ felhasználásával a felület (Surface) vagy görbe (Curve) objektumok közül választja.
Ismerjük meg ezek után röviden az EXPRESS legfontosabb alkotóelemeit.
Sémák.
A SCHEMA (séma) a modell összefoglaló szerkezete. A valamilyen szempontból közös információ összefogására szolgál. Minden egyéb EXPRESS deklarációnak valamely sémán belül kell elhelyezkednie. Az egyik sémában alkalmazott deklaráció felhasználható egy másik sémában is az interfész utasítások segítségével.
Séma szinten az ‘Example’ (Példa) nevű séma deklarálása grafikusan illetve szövegesen a következőképpen néz ki:

Mint már említettük valamely sémában deklarált elemek, esetleg az egész séma, felhasználható más sémákban is. Erre a műveletre két utasítás szolgál.
A USE FROM utasítás ENTITY (objektum) és TYPE (típus) deklarációkra utalhat és hatására a hivatkozott deklaráció mintegy bemásolódik az aktuális hivatkozási helyre.
A REFERENCE FROM utasítás, mely ENTITY (objektum), CONSTANT (konstans), FUNCTION (függvény), PROCEDURE (eljárás), TYPE (típus) deklarációkra utalhat. Ez az utasítás csak hivatkozik a külső deklarációra, eredményeképpen az nem válik a séma sajátjává.
Lássunk ezek után egy példát a USE FROM használatára.
Az exemple nevű séma deklarációjában felhasználjuk a references, geometry és definitons sémákból a length_measure (hosszmérték) és external_reference (külső referencia), vector (vektor) és direction (irány), illetve definition (definíció) és design_definition (tervezési definíció) objektumokat, illetve típusokat. Ezen kívül még deklarálunk a sémában egy új, item (elem) nevű objektumot, melynek description (leírás) nevű attribútumához a definition (meghatározás) nevű típust rendeljük. Ezt szabadon megtehetjük, mivel a definition deklarációját átvettük a USE FROM utasítással a definitons sémából, ami egyenértékű azzal mintha a deklarációt magában az exemple sémában végeztük volna el.
Természetesen a többi elem átvételének is csak akkor van értelme, ha a kérdéses séma deklarációjában felhasználásra kerülnek. Ettől azonban a könnyebb áttekinthetőség és helykímélés érdekében eltekintettünk.

Típusok.
Az EXPRESS-ben mint adatspecifikáló nyelvben különösen nagy szerepük van az adatok típusainak. Az adat típusok olyan értéktartományokat határoznak meg, melyeket a kérdéses elemek felvehetnek. Jellegük szerint az adat típusok: egyszerű adat típusok, gyűjtő adat típusok, definiált adat típusok, konstruált adat típusok és ál adat típusok lehetnek.
Felhasználás szerint az adat típusok jellemezhetnek egy attribútumot, lokális változót, formális paramétert, konstruált adat típust, definiált adat típust.
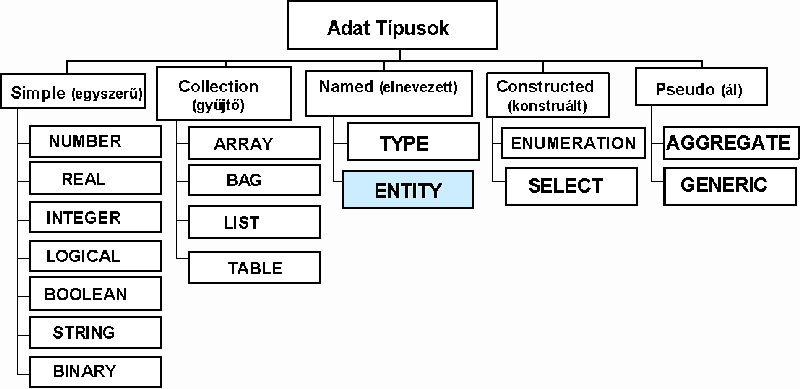
Az 5.58 ábrán bemutatjuk az adat típus csoportok alkotóelemeit, azaz a tulajdonképpeni típusokat.
|
5.58 ábra - EXPRESS adat típusok |
Az egyszerű adattípusok közismertek, talán csak a NUMBER (szám) és a LOGICAL (logikai) igényelhetnek egy kis magyarázatot. A NUMBER az INTEGER (egész) és a REAL (valós) egy csoportban történő összefoglalása, a LOGICAL pedig a TRUE (igaz) és FALSE (hamis) mellett az UNKNOWN (ismeretlen) értéket is felveheti.
Érdekesebbnek tűnnek a gyűjtő adat típusok.
Az ARRAY (tömb) adattípus egydimenziós, egész számokkal indexelt tömböket jelent. Ha többdimenziós tömböt akarunk specifikálni (pld. forgatási mátrixot) úgy a második dimenziót úgy hozhatjuk létre, hogy magukat a tömb elemeket is tömbként deklaráljuk. A tömb elemekre is alkalmazhatók a gyűjtő adattípusok kiegészítő jellemzői a UNIQUE (egyedi) és az OPTIONAL (esetleges). A UNIQUE azt jelenti, hogy a típust alkotó elemek nem lehetnek azonosak, az OPTIONAL specifikáció esetén pedig egy vagy több tömb érték határozatlan (?) lehet. Lássunk egy egyszerű példát:
szektorok : ARRAY [ 1 : 10 ] OF -- az első dimenzió
ARRAY [ 11 : 14 ] OF -- a második dimenzió
UNIQUE valami;
A deklaráció szerint a szektorok nevű attribútum 10 értéket tartalmaz négy elemű tömbökből, melyek elemei valami nevű adat típusúak (a valami típust valahol máshol már deklarálnunk kellett). A UNIQUE kulcsszó azt jelenti, hogy egy ARRAY [ 11 : 14 ]-n belül a valami értékei különbözőek kell, hogy legyenek, de két különböző ARRAY [ 11 : 14 ]-ban előfordulhat ugyanaz a valami érték.
A LIST kulcsszóval listát specifikálhatunk, mely hasonló elemek rendezett gyűjteménye, azaz az elemek elhelyezkedésük alapján érhetők el. Az alsó határ megadja a listában található elemek minimális számát, a felső határ pedig az elem szám maximumát. A felső határt lehet határozatlan értékként (?) is specifikálni.
A következő példában specifikált komplex_lista nevű típus zérustól tízig terjedő számú tömböt tartalmaz. A tíz egész számot tartalmazó tömböknek különbözniük kell egymástól egy konkrét listában:
komplex_lista : LIST [ 0 : 10 ] OF UNIQUE ARRAY [ 1 : 10 ] OF INTEGER;
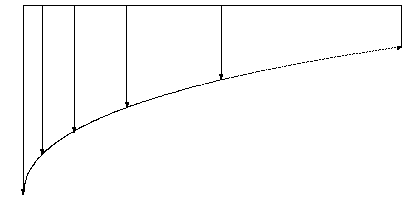
A TABLE (táblázat) olyan gyűjtemény, amelyben minden elemhez olyan, tetszőleges típusú indexet rendelünk, amelyik segítségével az elem azonosítható. A táblázatban lévő elemek száma az alsó és felső korláttal szabályozható. Ezzel a típussal például rögzíthetjük az alábbi süllyedési görbe (5.59 ábra) nem egyenletesen mintavételezett értékeit (azaz az abszcisszák lesznek az ordináták indexei):
sullyedes_tabla : TABLE [ 2 : ? ] OF hossz_egyseg INDEXED BY hossz_egyseg;
|
5.59 ábra - nem egyenletesen mintavételezett sűllyedési görbe |
Amint a példából látható a TABLE típus esetében az elemek típusán kívül meg kell adnunk az INDEXED BY kulcsszavakat követően az index típusát is, melynek jelen esetben az ordinátákkal azonosan a hossz egységet választottuk, melyet természetesen máshol deklarálni kellett.
A BAG (szatyor) hasonló elemek rendezetlen halmaza. Szintén rendelkezhet alsó és felső korláttal. A UNIQUE kulcsszó alkalmazása esetén nem tartalmazhat két azonos elemet. A nyelv korábbi verziójában erre az esetre külön típust SET (halmaz) specifikáltak. A következő egyszerű példában a pont_szatyor attribútumot, mint a korábban deklarált pont nevű definiált típusból megtöltött szatyrot deklaráljuk:
pont_szatyor : BAG OF pont ;
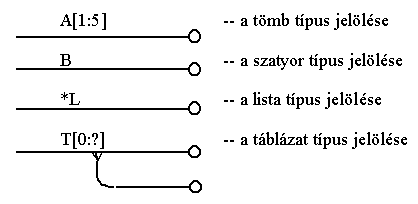
A gyűjtő adattípusok grafikusan a kapcsolatokat (relationship) kifejező vonalak segítségével kerülnek ábrázolásra, a vonalra ráírják a típus angol nevének első betűjét és az alsó és felső korlátot. A táblázat esetében egy külön, legyezőszerűen csatlakozó vonal mutat az index típusára. A UNIQUE kulcsszóval specifikált adattípus első betűjét * előzi meg.
Az elnevezett adattípusok közül először az objektum adattípussal (entity data type) ismerkedünk meg. Az objektum deklarációban szerepelnek attribútumok és attribútum típusok. Ez azt jelenti, hogy az objektum deklaráció tulajdonképpen meghatározza az objektum típusát. Ezt a típust az objektum azonosítóján keresztül érhetjük el. Példaként nézzük meg, hogy miként tudjuk a pont objektum típusának felhasználásával felépíteni a vonal objektumot. A vonal két attribútuma p0, p1 pont típusú azaz x, y, z valós attribútumokból (koordinátákból) áll.
ENTITY pont ; x, y, z : REAL ; END_ENTITY ; |
|
ENTITY vonal ; p0, p1 : pont ; END_ENTITY ; |
A csoport másik típusa a definiált adat típus külön deklarációban a TYPE kulcsszó felhasználásával készül. Minden így deklarált típusnak nevet kell adni. Példánkban azt mutatjuk be, hogy a definiált adattípussal közelebbről jellemezhetjük valamely attribútum valódi értelmét.
TYPE terfogat : REAL ; |
|
ENTITY RESZ ; ... terjedelem : terfogat ; END_ENTITY ; |
Példánkból jól látszik, hogy bár végső soron a terjedelem attribútum típusa valós, azzal hogy ezt a terfogat típuson keresztül deklaráltuk több információt nyújtottunk az attribútum lényegéről, mintha csak a REAL kulcsszót használtuk volna.
Gyakran előfordulnak a definiált adattípusokban az úgy nevezett tartomány szabályok (domain rules). Ezek a szabályok leszűkítik a típusban reprezentált értéktartományt. Jelölje a pozitiv típus a pozitív egész számokat:
TYPE pozitiv = INTEGER ; |
|
nemnegativ : SELF > 0 ; END_TYPE ; |
A példában található WHERE kulcsszó vezeti be a tartomány szabályt, melynek lehet neve (ez esetünkben nemnegativ) és tartalmaznia kell legalább egy SELF kulcsszót, mely ‘a szabálynak megfelelő típus elem’ szöveg helyett áll. Azaz ha szóban, magyarul próbáljuk elmondani ezt a típus meghatározást, akkor azt mondhatjuk, hogy ‘a pozitív típus olyan egész számokból áll, ahol érvényes a nem negatív szabály, mely szerint az egész szám (SELF) nagyobb zérusnál’.
A konstruált adat típusok közül először ismerjük meg a felsorolási adat típust.

Példánk jól illusztrálja, hogy ez a típus egy rendezett listában adja meg azokat az értékeket, melyeket az ilyen típusú attribútumok felvehetnek. A típusban szereplő új kulcsszó az ENUMERATION OF, mely után zárójelben következnek a lista elemei. A baloldali diagramon a datum objektumot és a nap_komponens attribútumon keresztül hozzá kapcsolódó het_nap felsorolási típus EXPRESS G szerinti jelölését mutattuk be.
A második konstruált adattípus a választ (select) listáján elnevezett adattípusok szerepelnek.

A példánkban valamely termék egyik attribútuma a termékre vonatkozó dokumentum(ok) és rajz(ok) azonosítóinak értékét veheti fel. A kérdéses típust a dokumentum és rajz entitásokra vonatkozó select típus különböző értékekkel rendelkező szatyor típusú aggregálásával értük el. A select típus tehát a listáján szereplő elnevezett típusok értéktartományának unióját specifikálja.
A pseudo típusok tulajdonképpen általánosított típusok, melyeket a függvények és eljárások formális paraméterinek specifikálására használnak.
Az AGGREGATE (halmozó) típus minden gyűjtő adattípus összefoglalását jelenti, míg a GENERIC (általános) minden más típus általánosítása.
A formális paraméter deklaráció során a fennemlített típusok még úgy nevezett típus címkével (types label) is ellátandók, ha a deklarált típust alkalmazzuk lokális váltózók vagy az eredmény típusának specifikálására is.
A példaként bemutatott scale függvény megszorozza egy valós számmal a bemenő valós számokat.
FUNCTION scale (input : AGGREGATE : intype OF REAL;
scalar : REAL) : AGGREGATE : intype OF REAL;
LOCAL
result : AGGREGATE : intype OF REAL;
END_LOCAL;
REPEAT i := LOINDEX(input) TO HIINDEX(input);
result [i] := scalar * input [i];
END_REPEAT;
RETURN(result);
END_FUNCTION;
A példa első szava a függvény deklaráció kulcsszava a FUNCTION (az utolsó pedig a függvényt záró END_FUNCTION), ezután jön a függvény neve, majd zárójelben egymástól ':' -al elválasztva az input formális bemenő paraméter, a paraméter típusa - AGGREGATE, majd az intype típus címke. Az ezután következő OF REAL megmondja, hogy miből történt az aggregálás. A : intype el is hagyható, ha nem kívánjuk a típust a formális paramétereken kívül még az eredményül kapott függvényérték, illetve az algoritmus helyi változóinak specifikálására is felhasználni. Esetünkben azonban mind a függvény, mind pedig a result helyi változó AGGREGATE típusú, ezért deklarációjukban szerepelnie kell a formális paraméterrel kapcsolatban bevezetett címkének.
Maga az algoritmus igen egyszerűen olvasható, a vele kapcsolatban bevezetett, még nem említett kulcsszavak a LOCAL ... END_LOCAL pár a helyi változók deklarálására, a REPEAT ... END_REPEAT pedig ciklus utasítás, melyben a ciklus változó értéke (i := LOINDEX() TO HIINDEX()) a zárójelben elhelyezett paraméter alsó indexétől a felső indexéig változik, a RETURN() a zárójelben lévő változó értékét átadja a függvénynek.
A GENERIC típus alkalmazása esetén a formai szabályok azonosak az AGGREGATE-nál megismertekkel, ezért az ismétlések helyett lássunk itt is egy példát. A példa egy általános összeadási függvény specifikálása lesz. mely számokat vagy vektorokat ad össze:
FUNCTION add (a, b : GENERIC : intype) : GENERIC : intype;
LOCAL
nr : REAL;
vr : vector;
END_LOCAL;
IF ( _real IN typeof(a)) AND ( _real IN typeof(b)) THEN
nr :=
a+b;
RETURN(nr);
ELSE
IF ( vector IN typeof(a)) AND ( vector IN typeof(b)) THEN
vr :=
vector(a.i + b.i, a.j + b.j, a.k + b.k);
RETURN(vr);
END_IF;
END_IF;
RETURN(?); -- ervenytelen bemenet eseten a visszaadott ertek hianyzik
END_FUNCTION;
Ahhoz, hogy a példát egyszerűen olvashassuk bevezetőben meg kell jegyeznünk, hogy az úgynevezett 'típus név adat típus' úgy képezhető a beépített adattípusokból, hogy a kisbetűvel írt típus név elé egy aláhúzás karaktert helyezünk, azaz a _real értéke REAL.
A typeof(v) függvény visszaadja mind azoknak az adattípusoknak a nevét melyeknek a v formális paraméter a tagja. Az IN kulcsszó pedig a bennfoglalást reprezentálja.
Az add függvény a, b formális paramétereit, illetve magát függvényt is GENERIC típusúnak deklaráltuk. A két helyi változó közül nr valós, vr pedig vector típusú (a vector-t korábban típus deklarációval meg kellett határoznunk).
Megvizsgáltuk, hogy mind az a mind a b típusa valós-e és ha igen összeadva öket megkaptuk nr-t és ezzel tettük egyenlővé a függvény visszaadott értékét.
Ha a mindkét típus ugyan nem valós, de vektor típus volt, úgy létrehoztuk vr-t mint az a és b vektorok komponensenkénti összegét.
Ha egyik feltétel sem volt igaz a bemenő adatok típusaira, úgy amint azt a megjegyzés sorban (két - karakter után) jeleztük a függvény nem szolgáltat kimeneti értéket.
Konstansok.
A konstansok mint közismert olyan értékek, melyek a program végrehajtása során nem változnak. Az EXPRESS nyelvben lehetőség van nevezett konstansok deklarálására a CONSTANT kulcsszó felhasználásával. A deklarálás során a konstansnak értéket kell adni, mely a további specifikációkban már nem változhat. Ennek a viszonylag egyszerű szerkezetnek a struktúráját legcélszerűbb példával illusztrálni:
CONSTANT
ezer : REAL := 1000;
millio : REAL := ezer**2;
kezdopont : pont := pont(0.0,
0.0, 0.0);
END_CONSTANT;
Az első és második deklaráció illetve inicializálás abból a szempontból érdekes, hogy a millio deklarálásában már felhasználtuk az előtte deklarált ezer konstanst. A kezdopont deklarálása viszont feltételezte, hogy korábban valahol már deklaráltuk a pont entitást, ahogy ezt valóban meg is tettük, és ennek az entitásnak egy konkrét értékkel felruházott példányából képeztünk nevezett konstanst.
A nevezett konstansokon kívül az EXPRESS nyelv rendelkezik egy sor egzakt értékűnek tekintett beépített konstanssal. Ezek a következők:
CONST_E - REAL típusú konstans, a
természetes logaritmus alapja, meghatározási képlete: 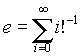 .
.
PI - REAL típusú konstans, a közismert p szám (a kör kerületének viszonya az átmérőhöz).
? - a határozatlan értéket kifejező konstans, valamennyi adattípussal kompatibilis, rendszerint a gyűjtő adattípusok határozatlan felső határának kijelölésére használják.
TRUE, FALSE, UNKNOWN három logikai (LOGICAL) típusú konstans, melyek közül az első kettő a BOOLEAN típussal is kompatibilis.
SELF az aktuális objektum példányra vagy típus értékre történő hivatkozás. Bár a SELF tulajdonképpen nem konstans, azokon a helyeken ahol alkalmazzák (tulajdonság specifikáció, objektum deklaráció, típus deklaráció és objektum konstruktor) konstansként viselkedik.
Objektumok.
Az objektum (ENTITY) olyan információk osztálya, mely közös tulajdonságokkal rendelkező fizikai vagy elvont objektumokat reprezentál.
Amint azt az objektum típus deklarációjával kapcsolatban már láttuk, az objektum deklarációja során nevet adunk a típusnak, specifikáljuk attribútumait, viselkedését és korlátozásait.
|
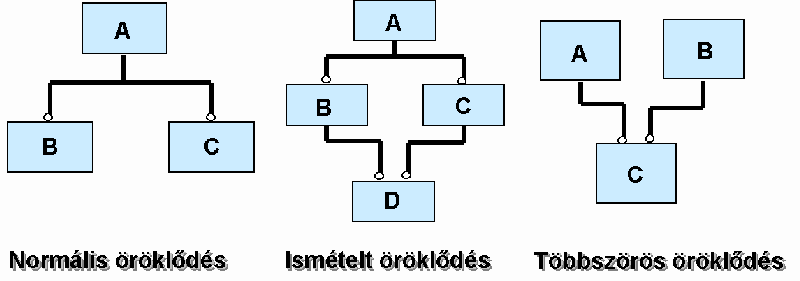
5.60 ábra - öröklődési alternatívák az EXPRESS nyelvben |
Mivel az EXPRESS objektum orientált elveken nyugszik, lehetővé teszi az entitások hierarchikus származtatását: a specializálást és a generalizálást. Arról van tulajdonképpen szó, hogy az egymással rokon entitás típusok lehetnek általánosabbak (csak a legfontosabb attribútumokat, korlátozásokat tartalmazók) ezeket szuper típusoknak (SUPERTYPE) nevezzük és lehetnek részletesebbek ezek az altípusok (SUBTYPE). Az altípusok öröklik a szuper típusuk, illetve szuper típusaik összes tulajdonságát: attribútumait, és korlátozásait. Az EXPRESS nyelv lehetővé teszi a többszörös öröklést ezért egy altípusnak több szuper típusa is lehet. Természetesen egy altípus maga is lehet egy még specializáltabb leszármazottjának szuper típusa. Az azonban ki van zárva, hogy egy altípus önmagának szuper típusa legyen, azaz a ciklikus gráfok nem engedélyezettek.
Az 5.60 ábrán bemutattuk az öröklődés lehetséges variánsait.
A szuper típusokból származó altípusok különböző mértékben fedhetik is egymást egy-egy konkrét összefüggésben. Bizonyos összefüggések azt igénylik, hogy a szupertípust csak altípusain keresztül 'példányosítsuk' (instantiate) (magyarul konkretizáljuk, azaz pld. a személyek típusból kiválasszunk egy konkrét személyt pld. Nagy Istvánt). Az ilyen szupertípust absztrakt szuper típusnak (ABSTRACT SUPERTYPE) nevezzük, és ezt a tulajdonságát az EXPRESS új verziója a kérdéses összefüggést is specifikáló altípus korlátozó (SUBTYPE_CONSTRAINT) szerkezetben specifikálja. A régi, ma még hivatalos verzióban a szuper típust az objektum deklarációban kellett szerepeltetni. Az altípus korlátozásokra vonatkozó példáinkat az új verzió szellemében készítettük, de ezek után, visszatérve a hajós példánkhoz bemutatunk egy korlátozás nélküli absztrakt szuper típus - altípus példát is, a régi verzió szerint.
Lássuk tehát a lehetőségeket, egy-egy példával alátámasztva.
- Az altípusok bizonyos összefüggésben (témában) teljesen lefedik a szuper típust. Azoknak az altípusoknak melyekre ez igaz szerepelniük kell a kérdéses téma altípus korlátozásában TOTAL_OVER specifikációval. Példánkban a személy szuper típust bontjuk férfi, nő és alkalmazott altípusokra és a személy neme témában jelöljük ki a személyt absztrakt szupertípusnak, melyet a nők és férfiak altípusai teljesen lefednek. Talán belátható az absztrakt szupertípus jogosultsága ebben az aspektusban, hiszen ha egy nőt vagy férfit akarunk konkretizálni az csak az altípusok segítségével lehetséges.
ENTITY szemely;
nev : szemely_nev;
END_ENTITY;
ENTITY ferfi SUBTYPE OF
(szemely);
...
END_ENTITY;
ENTITY no SUBTYPE OF
(szemely);
...
END_ENTITY;
ENTITY alkalmazott SUBTYPE OF
(szemely);
...
END_ENTITY;
SUBTYPE_CONSTRAINT szemely_neme FOR
szemely;
ABSTRACT SUPERTYPE;
TOTAL_OVER (ferfi, no);
END_SUBTYPE_CONSTRAINT;
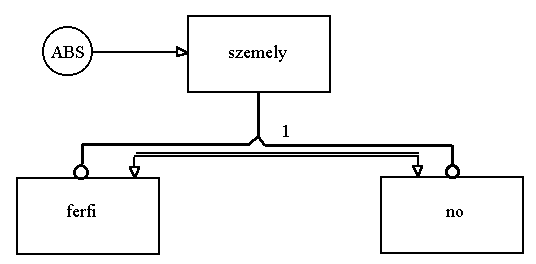
Rajzoljuk is meg ezt a feladatot az EXPRESS-G új verziójának jelölésrendszerében. Megjegyezzük, hogy ebben az absztrakt osztályt a körbe helyezett ABS, a teljes lefedést pedig a két párhuzamos vonal jelképezi.
|
5.61 ábra - az absztrakt szupertípus és a teljes lefedés ábrázolása az EXPRESS-G nyelvben |
- Ha az altípus téma szerinti korlátozási listáján szereplő absztrakt szuper típus attribútum típusai közül csak egy-egy szerepelhet az altípusokban ezt a ONEOF kulcsszóval kell specifikálni. Példánkban témaként a háziállatok fajta szerinti szétválasztását jelöltük meg.
ENTITY allat;
nev
: allat_nev;
...
END_ENTITY;
SUBTYPE_CONSTRAINT szeparal_fajtat FOR allat;
ABSTRACT
SUPERTYPE;
ONEOF (macska,
nyul, kutya, ...);
END_SUBTYPE_CONSTRAINT;
ENTITY macska
SUBTYPE OF (allat);
...
END_ENTITY;
ENTITY nyul
SUBTYPE
OF (allat);
...
END_ENTITY;
ENTITY kutya
SUBTYPE
OF (allat);
...
END_ENTITY;
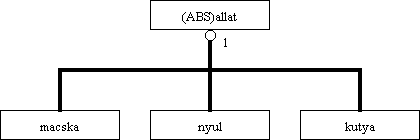
Az 5.62 ábrán a ProSTEP német cég EXPRESS Modeller nevű CASE programjával megrajzoltuk az állatosztályozós példát. El kell mondanunk, hogy a korlátozásokra a ONEOF kivételével a jelenleg érvényes verzióban nincs jelölés, a következő verzióban tervezik a TOTAL_OVER korlátozás szimbólumának a bevezetését. |
|||
|
- Ha a szuper típus egy példánya több altípusnak is példánya lehet, úgy az altípus korlátozást ANDOR kulcsszóval kell specifikálni. Példánkban azt mutatjuk be, hogy ha a személy szupertípust alkalmazott és diák altípusra bontjuk a tanulhat_az_alkalmazott_is téma szempontjából az altípusokat ANDOR kulcsszóval specifikáljuk, mivel az alkalmazott lehet egyben diák is, ha beiratkozik az esti tagozatra.
ENTITY szemely;
nev : szemely_nev;
END_ENTITY;
SUBTYPE_CONSTRAINT tanulhat_az_alkalmazott_is FOR szemely;
alkalmazott ANDOR diak;
END_SUBTYPE_CONSTRAINT;
ENTITY alkalmazott SUBTYPE OF (szemely);
...
END_ENTITY;
ENTITY diak SUBTYPE OF (szemely);
...
END_ENTITY;
- Az AND kulcsszóval olyan csoportosítások közötti kapcsolatot tudunk kifejezni, melyeket más szupertípus / altípus korlátozásokkal hoztunk korábban létre. Deklaráljuk a szemely szuper típust, mely a ferfi no és allampolgar kulfoldi csoportosításokat is lehetővé teszi.
ENTITY szemely SUPERTYPE OF (ONEOF(ferfi, no) AND ONEOF(allampolgar, kulfoldi));
nev : szemely_nev;
END_ENTITY;
ENTITY ferfi SUBTYPE OF (szemely);
...
END_ENTITY;
ENTITY no SUBTYPE OF (szemely);
...
END_ENTITY;
ENTITY allampolgar SUBTYPE OF (szemely);
...
END_ENTITY;
ENTITY kulfoldi SUBTYPE OF (szemely);
...
END_ENTITY;
Végül lássuk a korlátozás nélküli, absztrakt szuper típus / altípus kapcsolatot bemutató hajógyártási példánkat, melyet a többi hajós példával együtt az EPM cég Interneten hozzáférhető bevezető oktató anyagából magyarítottunk, illetve kölcsönöztünk.
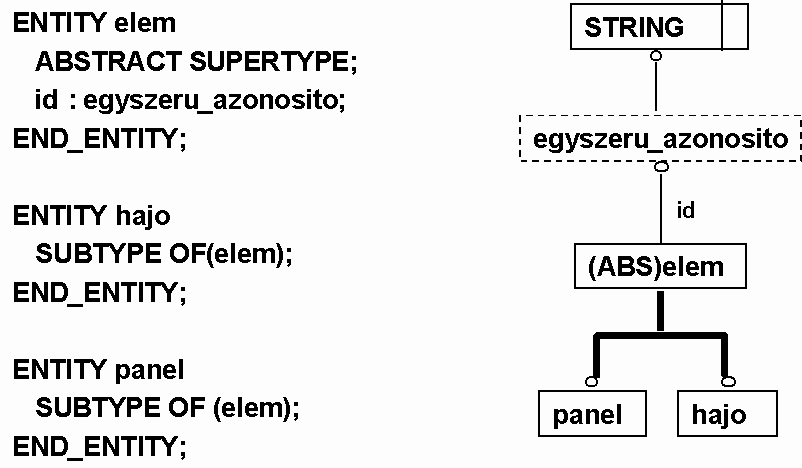
Attribútumok.
Az objektumok tulajdonságait, jellemzőit, minőségét az attribútumok határozzák meg. Az EXPRESS nyelv három féle attribútumot különböztet meg:
- Az explicit attribútum értékét az implementáció során kell megadni az objektum példányosítási folyamatban.
- A levezetett (derived) attribútum értékét valamilyen számítás szolgáltatja.
- Az inverz (inverse) attribútum értéke azt az objektum példányt tartalmazza, mely valamilyen célból felhasználja az objektumot.
Az explicit attribútumoknak az objektum minden példányában értéket kell kapniuk, ha csak nincsenek az OPTIONAL kulcsszóval deklarálva. Ha az attribútumot nem absztrakt osztályban deklarálják típusa nem lehet áltípus.
Lássunk ezután egy egyszerű példát.
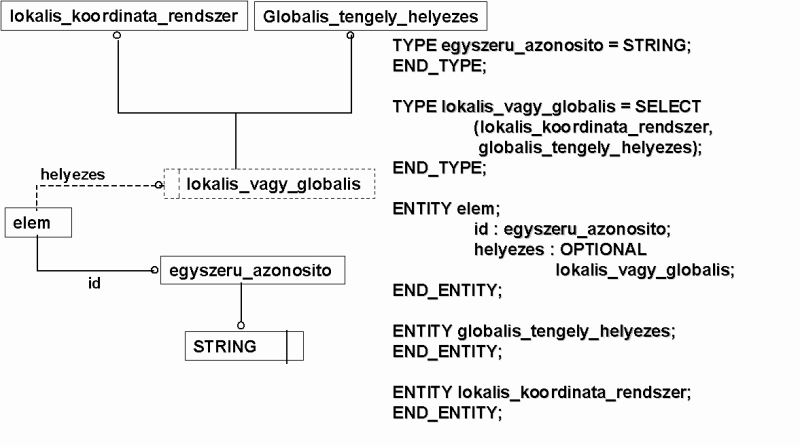
Lássunk egy másik, egyszerűbb példát is, határozzuk meg a pont entitást a pontot alkotó három koordináta mint explicit attribútum felhasználásával.
ENTITY pont;
x, y, z : REAL;
END_ENTITY;
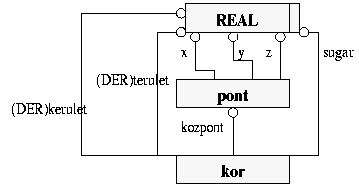
A levezetett (derived) attribútumokat valamely matematikai kifejezés kiértékelése szolgáltatja. Az előző példánkra támaszkodva deklaráljunk egy kör objektumot, mely levezetett attribútumaiként határozzuk meg a területét és kerületét.
ENTITY kor; kozpont
: pont; DERIVE terulet : REAL := PI*sugar**2; END_ENTITY; |
|
Amint a példa EXPRESS-G reprezentációjából látható, a levezetett attribútumokat az azonosítójuk elé helyezett (DER) betűkombinációval különböztetjük meg. Azt már csak ismétlésképpen jegyezzük meg, hogy az attribútumokat a birtokló objektumból a típus szimbólumba tartó, üres körrel végződő vonallal jelöljük, azonosítójukat pedig a vonal mellé írjuk.
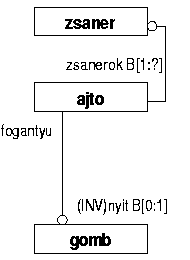
Talán legbonyolultabb lesz megértenünk az inverz (inverse) attribútum fogalmát. Ha egy objektum explicit argumentum segítségével kapcsolatra lépett egy aktuális objektummal, úgy az inverz attribútum arra használható, hogy ezt a kapcsolatot pontosítsa az aktuális objektum szempontjából. Az alábbi példánk talán világosabbá teszi a problémát.
Deklaráljuk az ajtó objektumot fogantyú és zsanérok explicit attribútumokkal. A fogantyú gomb (objektum) típusú. Ezután a gombot deklaráljuk az inverz attribútummal arra utalva, hogy a gomb vagy még nincs felszerelve az ajtóra, vagy már fel van szerelve fogantyúvá, de mindenképpen csak az a szerepe, hogy fogantyú legyen, azaz a gomb objektum szempontjából a más irányú felhasználás nem létezik.
ENTITY ajto; fogantyu
: gomb; END_ENTITY; ENTITY gomb; ... INVERSE nyit : BAG [0:1] OF ajto FOR fogantyu; END_ENTITY; |
|
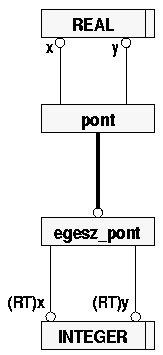
A szuper típusban deklarált attribútumok öröklődnek az altípusokban. Előfordul azonban, hogy az altípusban szűkíteni kell az attribútum lehetséges értéktartományát, ezt az attribútum újra deklarálásával (redeclaration) érhetjük el. Az újradeklarálás során a tartomány szűkítés az alapszabály. E mellett lehetőség van az explicit attribútum levezetett attribútumra cserélésére, az opcionális attribútum kötelezővé változtatására, a LIST és a BAG típusok határspecifikációinak szűkítésére. Az új EXPRESS verzióban lehetséges lesz a névváltoztatás is bizonyos feltételek mellett. Formailag az újradeklarálást a SELF\<szupertípus név>.<attribútum név> szerkezettel oldják meg (ez helyettesíti az objektum deklarációban az attribútum nevét).
Első példánkban a pont szuper típus egesz_pont altípusa a koordináták típusát valósról egészre szűkíti
ENTITY pont; x : REAL; END_ENTITY; ENTITY egesz_pont; SUBTYPE
OF (pont); END_ENTITY; |
|
Második példánkat a már hivatkozott EPM oktató anyagból kölcsönöztük illetve magyarítottuk. A feladat lényege, hogy az elem szupertípusban meghatározott 'helyezes' attribútum típusát leszűkítjük, mivel nem tesszük lehetővé a választást a helyi és globális koordináta rendszerek között, e mellet opcionálisból kötelezőre változtatjuk.

Szabályok.
A típusokkal kapcsolatban már említettük a tartományi szabályokat, most megpróbáljuk összefoglalni az objektum deklarációhoz kapcsolható szabályok témakörét.
Lokális és globális szabályok segítségével kiegészítő feltételeket lehet állítani az attribútum tartományokra.
A lokális szabályok egy objektum valamennyi példányára érvényes korlátozásokat deklarálnak. A szabályt az objektum deklarációban elhelyezett UNIQUE illetve WHERE kulcsszavak segítségével lehet specifikálni.
A különbözőségi szabály vonatkozhat egy vagy több attribútumra. Az első esetben az az értelme, hogy a kérdéses attribútum minden objektum példányban különböző kell hogy legyen. A második esetben, ha több attribútumra vonatkozik, úgy tiltja az azonos kombinációkat.
Első példánkban azt a megkötést deklaráljuk, hogy minden TAJ számnak különbözőnek kell lennie.
ENTITY szemely;
taj_szam : INTEGER;
nev : STRING;
UNIQUE
ur1 : taj_szam;
END_ENTITY;
Második példánk több attribútumra vonatkozik. Ebben a példában megengedjük, hogy két személynek azonos neve legyen, de a neve és a kitűzője sorszáma nem lehet azonos.
ENTITY szemely_nev;
vezetek : STRING;
kereszt : STRING;
apai : STRING;
becenev : STRING;
END_ENTITY;
ENTITY alkalmazott;
kituzo : INTEGER;
nev : szemely_nev;
...
UNIQUE
ur1 : kituzo, nev;
...
END_ENTITY;
A példában szereplő ur1 a különbözőségi feltétel azonosítója.
A tartományi szabályok logikai (TRUE, FALSE, UNKNOWN) értékűek vagy határozatlanok (?). A szabályok a WHERE kulcsszóval kezdődnek és hivatkozni kell bennük vagy a SELF kulcsszóra, mely a deklarált objektum egy példányát jelenti, vagy magában a deklarációban vagy a szuper típus(ok) deklaráció(i)ban szereplő attribútumokra.
Példánkban azt a feltételt fogjuk a szabállyal érvényre juttatni, hogy az egység vektorok hossza minden esetben pontosan az egység. A szabály neve esetünkben hossz_1.
ENTITY egyseg_vektor;
a, b, c : REAL;
WHERE
hossz_1 : a**2 + b**2 + c**2 = 1.0;
END_ENTITY;
A globális szabály vagy egy objektum teljes értéktartományát, vagy egynél több objektum példányait együttesen korlátozza. Formailag a szabály a RULE <szabály_név> FOR (objektum_1, objektum_2, ...) <algoritmus> END_RULE; kulcsszó és tartalmi együttessel írható le. Az <algoritmus> természetesen újabb kulcsszavakat, függvényeket, tartományi szabályokat tartalmazhat.
Mielőtt a példánkra rátérhetnénk bemutatjuk a sizeof függvényt, mely megadja az argumentumában szereplő aggregált érték elem számát, majd meg kell hogy ismerjük a QUERY kifejezést, mivel ez szinte minden szabályban alkalmazásra kerül. A kifejezés összehasonlítja egy aggregált érték minden elemét egy logikai kifejezés segítségével és összeállít egy olyan korlátozott aggregált értéket, mely elemei a logikai kifejezésben TRUE-nak bizonyultak.
Formailag a kifejezés a következőképpen néz ki: QUERY( valtozo_nev <* <aggregált érték neve> | logikai kifejezés ). A <* speciális műveleti jel.
Lássunk ezek után példát a QUERY-re.
Tételezzük föl, hogy a szin egy olyan definiált típus, melynek alap típusa ENUMERATION (felsorolás), mely magában foglalja a rozsaszin és voros értékeket is. A következő példa segítségével ki fogjuk vonni a szinek tömbből a pirosnak tekinthető rozsaszin és voros értékeket.
LOCAL
szinek : ARRAY OF szin;
pirosok : ARRAY OF OPTIONAL
szin;
END_LOCAL
...
pirosok := QUERY ( elem <* szinek | (elem = rozsaszin) OR (elem = voros));
...
Példánkban tehát a változót, mely sorra felveszi az aggregált érték elemeinek értékeit elem-nek neveztük, a vizsgált aggregált érték a szinek tömb volt, a logikai kifejezés pedig akkor volt igaz, ha az elem rozsaszin vagy voros volt.
Térjünk vissza ezután a globális szabály megvilágítására szolgáló példánkhoz. A koordináta síkok a teret nyolc részre osztják. A következő szabály azt követeli meg, hogy az első és hetedik nyolcadban azonos legyen a pontok száma.
RULE
pont_passzol FOR (pont);
LOCAL
elso_nyolcad,
hetedik_nyolcad : BAG OF
UNIQUE pont := []; --
ures pont szatyor
END_LOCAL;
elso_nyolcad := QUERY(temp <*
pont | (temp.x > 0) AND (temp.y > 0) AND (temp.z > 0) );
hetedik_nyolcad := QUERY(temp
<* pont | (temp.x < 0) AND (temp.y < 0) AND (temp.z < 0) );
WHERE
SIZEOF(elso_nyolcad) = SIZEOF(hetedik_nyolcad);
END_RULE;
Beépített elemek.
Bár amint már említettük az EXPRESS nem programozási nyelv, a kifejezések, újradeklarálások, szabályok, függvénydeklarációk, stb. céljaira részben szükséges, részben kényelmi célokat szolgálnak a nyelvbe beépített elemek. Ilyen elemekkel példáink kapcsán esetenként már találkoztunk, a következőkben rendszerezetten, de nagyon röviden szeretnénk összefoglalni a beépített függvényeket, eljárásokat, utasításokat, operátorokat. Ismét felhívjuk az érdeklődők figyelmét, hogy szabatos részletes meghatározásokat magában a szabványban találnak. Mivel azonban a szabvány csak jelentős idő és pénz ráfordítással szerezhető be, olcsóbb és kényelmesebb a nyelv 2. verziójának referencia kézikönyvét letölteni az Internetről.
- Beépített függvények:
o abs ( v ) a v valós argumentum szintén valós abszolút értéke;
o acos ( v ) a (-1 <= v <= +1) közötti valós argumentum koszinusz értéknek megfelelő valós szög (0 p) radián tartományban;
o asin ( v ) a (-1 <= v <= +1) közötti valós argumentum szinusz értéknek megfelelő valós szög (-p/2 +p/2) radián tartományban;
o atan (v1, v2) a v=v1/v2 valós típusú hányadossal kifejezett tangens értéknek megfelelő valós szög (-p/2 +p/2) radián tartományban, ha v2=0, úgy az eredmény -p/2 vagy +p/2 a v1 előjelétől függően;
o blength ( v ) a függvény egész típusú eredménye a v bináris szám bitjeinek számát szolgáltatja;
o cos ( v ) a radiánban kifejezett valós típusú v szög koszinusza;
o exists ( v ) a függvény BOOLEAN típusú eredménye attól függően igaz vagy hamis, hogy a tetszőleges típusú eredményt szolgáltató v kifejezésnek van e aktuális eredménye vagy az eredmény határozatlan;
o format ( n:COMPLEX; f:STRING ) az n komplex számot átalakítja az f-ben magadott formátumú sztringgé;
o hibound ( v ) megadja a vaggregált típusú argumentum egész típusú felső határát;
o hiindex ( v ) megadja a felső index egész típusú értékét, ha a v tömb, illetve az elemek számát ha a v szatyor vagy lista típusú;
o length ( v ) megadja a v sztringben található karakterek egész típusú számát;
o lobound ( v ) megadja a vaggregált típusú argumentum egész típusú alsó határát;
o log ( v ) megadja a valós típusú v természetes logaritmusát;
o log2 ( v ) megadja a valós típusú v kettő alapú logaritmusát;
o log10 ( v ) megadja a valós típusú v tíz alapú logaritmusát;
o loindex ( v ) megadja az alsó index egész típusú értékét, ha a v tömb, illetve egyet (1), ha a v szatyor vagy lista típusú;
o nvl ( v, substitute ) ha a v tetszőleges típusú kifejezés határozatlan értékű (?), úgy a substitute szintén tetszőleges típusú kifejezés értékét adja vissza a függvény, ellenkező esetben a visszaadott érték megegyezik v-vel, a substitute értéke nem lehet határozatlan;
o odd ( v ) a visszaadott érték igaz, ha az egész típusú v páratlan;
o rolesof ( v ) a függvény v paramétere valamely objektum adattípus bármely példánya, visszaadott értéke pedig olyan különböző objektum példányok attribútum szerepneveiből álló szatyor, melyek használják a paraméterben megadott példányt;
o sin ( v ) a radiánban kifejezett valós típusú v szög szinusza;
o sizeof ( v ) a függvény visszaadott értéke egész típusú és azt mondja meg, hogy az aggregált típusú v paraméter hány elemet tartalmaz;
o tan ( v ) a radiánban kifejezett valós típusú v szög tangense;
o truncate ( v ) a függvény csonkolja a v-ben megadott valós számot és a benne foglalt legnagyobb egész értéket adja vissza;
o typeof ( v ) a függvény visszaadja az azok által a típus nevek által alkotott szatyrot, mely típusoknak a paraméter tagja;
o usedin ( r , t ) a függvény visszaadott értéke egy olyan szatyor, mely tartalmazza mindazokat az objektum példányokat, melyek a t objektum példányt r szerepkörben (például egy pontot kör középpontként) használnak;
o value ( v ) a sztring típusú v paraméter értékéből annak formátuma alapján valós, egész vagy komplex értéket ad vissza, ha a sztring nem értelmezhető számként, úgy a válasz érték határozatlan (?);
o value_unique ( v ) igaz értéket ad vissza, ha a paraméterként megadott aggregált típusban minden elem különböző értékű, ellenkező esetben a válasz hamis, ha pedig v határozatlan (?) a válasz ismeretlen.
- Néhány beépített eljárás:
o insert (VAR l, e, p ) az eljárás eredményeképpen az e példány beszúródik az l lista p sorszámú helyére, feltétel hogy a lista elemeinek típusa megegyezzen a beszúrandó példány típusával;
o remove (VAR l, p ) törli az l lista p-ik elemét.
- Néhány utasítás:
Az utasításokat függvényekben, eljárásokban, szabályokban alkalmazzák és csak az ezekben a struktúrákban deklarált helyi változókra hatnak.
o ; az önmagában, külön sorban álló pontos vesszőt nulla utasításnak nevezik - hatására semmi sem történik;
o ALIAS valtozo_azonosito FOR altalanos_referencia ; utasitas(ok) END_ALIAS;
a változó azonosító általában egy rövid név amivel az objektum attribútum öröklődés miatt hosszú nevét a végrehajtandó utasításokba való beíráshoz le lehet rövidíteni;
o parameter_vagy_valtozo_hivatkozas := kifejezes ;
a program nyelvekből jól ismert értékadó utasítás;
o CASE valaszto_kifejezes OF cimke_kifejezes : utasitas ;
cimke_kifejezes : utasitas ;
...
cimke_kifejezes : utasitas ;
OTHERWISE
: utasitas ;
END_CASE ;
A CASE utasítás is jól ismert a program nyelvekből - a választó kifejezés kiszámolja, hogy a program melyik ága (melyik címkével ellátott utasítása) kerül végrehajtásra. Ha a választó kifejezés értéke egyik címkével sem esik egybe, akkor vagy semmi sem hajtódik végre, vagy ha az opcionális OTHERWISE specifikáció is szerepel, akkor az utána következő utasítás;
o Az utasítás zárójelet itt is a BEGIN ... END pár reprezentálja, a pontok helyén utasítások állnak pontos vesszővel elválasztva, melyek egy utasításnak tekintendők;
o Az ESCAPE ; utasítás a REPEAT ciklus utasításon belül használva lehetővé teszi a ciklus megszakítását;
o A logikai elágazást az EXPRESSben is a IF logikai_kifejezes THEN utasitas ELSE utasitas END_IF; szerkezettel oldhatjuk meg. Ha a logikai kifejezés igaz, úgy a THEN utáni, ha hamis az ELSE utáni utasítás hajtódik végre;
o Az eljárás hívási utasítás nem más, mint az eljárás neve és utána zárójelben, egymástól vesszővel elválasztva az aktuális paraméterek következnek. Mint minden utasítást ezt is pontosvesszővel zárjuk;
o A ciklus utasítást az EXPRESS a REPEAT repeat_control ; utasitas END_REPEAT; szerkezettel valósítja meg.
A ciklus vezérlésére (amit az utasításban repeat_control-lal jelöltünk) négy lehetőség van, melyek kombináltan is használhatók.
§ Az első lehetőség az aggregált vezérlés, formája a következő: FOREACH valtozo_azonosito IN aggregált_objektum. A változó azonosítót explicite olyan típusúnak kell deklarálni mint amilyenek az aggregált objektum (lista, tömb, szatyor) elemei. A változó sorra felveszi az elemek értékét és valamennyivel lefut a ciklus mag.
§ A második lehetőséget az inkrementális vezérlés biztosítja. Formailag ez a struktúra a következőképpen néz ki: valtozo_azonosito := hatar_1 TO hatar_2 [ BY novekmeny ]. A kifejezésben szereplő változó először felveszi az alsó határ értékét, majd lefuttatja a ciklus magját, ezután növeli értékét az opcionális növekménnyel (ha ez nincs megadva eggyel) újra futtatja a ciklus magot és mindez addig ismétlődik míg a változó értéke nem haladja meg a felső határt.
§ A harmadik lehetőség a WHILE (mindaddig) vezérlés. WHILE logikai_kifejezes. Mielőtt a ciklus mag lefut a ciklus utasítás kiértékeli a logikai kifejezést és csak akkor kezdi végrehajtani a mag utasításait ha a kifejezés értéke TRUE (igaz).
§ Lényegében nagyon hasonló az UNTIL (ig) vezérlés is. UNTIL logikai_kifejezes. A ciklusmag először lefut, utána értékeli ki, hogy a kifejezés értéke igaz-e, ha igaz újra lefut és ez mindaddig folytatódik amíg a kifejezés értéke hamissá nem válik. Azaz ez a vezérlési típus biztosítja, hogy a ciklus mag legalább egyszer mindíg lefusson;
o A RETURN utasítás a függvény vagy eljárás befejezését jelzi. Függvény esetén RETURN (kifejezes) alakot használunk, ahol a kiértékelt kifejezés jelenti a függvény visszaadott értékét. Eljárás esetén a RETURN önmagában áll;
o A SKIP utasítás segítségével a ciklusmagban átugorhatjuk az utána következő utasításokat és az END_REPEAT-re adjuk a vezérlést, ami azt jelenti hogy innen a ciklus úgy folytatódik mint ha mi sem történt volna.
- Beépített operátorok.
A kifejezésekben szereplő objektum példányokkal az operátorok segítségével hajthatunk végre különböző műveleteket. Az operátorokkal műveletbe hozott példányokat operandusoknak hívják. Egyes operátoroknak egy operandusuk van, másoknak kettő. Az első esetben az operátor megelőzi az operandust, a második esetben pedig az operátor a két operandus között helyezkedik el.
A beépített operátorokat a következőképpen csoportosíthatjuk:
o aritmetikai operátorokkal különböző típusú számokkal végezhetünk műveleteket. Az összeadás, kivonás, szorzás, osztás, hatványozás, egész osztás és modulus képzés műveleti jeleit látjuk a bekezdés utolsó sorában. Az egész osztás eredménye a hányados egész része, míg a modulus azzal a maradékkal egyenlő amit úgy kapunk meg hogy megszorozva az osztót az egész osztás eredményével kivonjuk az osztandóból
+ - * / ** DIV MOD
o relációs operátorokkal össze tudjuk hasonlítani az objektumokat illetve attribútumaikat. A felsorolt szimbólumok: egyenlő, nem egyenlő, nagyobb mint, kisebb mint, nagyobb egyenlő, kisebb egyenlő, példány egyenlő, példány nem egyenlő különböző típusok esetére részletesen specifikálhatók. Ezeknek a specifikációknak a gyűjtő jellegű adattípusoknál van különös jelentősége. Az IN operátor értéke TRUE ha a baloldali operandus szerepét játszó elem példány egyenlő a jobboldali operandust alkotó gyűjtő típusú objektum valamely elemével. A LIKE operátor két sztringet hasonlít össze, értéke TRUE ha a két sztring minden megfelelő eleme azonos
= <> > < >= <= :=: :<>: IN LIKE
o sztring indexeléssel ki tudunk választani a sztringből egy karaktert (ha a sztring neve után tett kapcsos zárójelbe egy számot írunk), illetve egy karakter sorozatot ha a kapcsos zárójelbe kettősponttal elválasztva az első és utolsó karakter sorszáma kerül. Az összefűzést (konkatenálást) jelző + operátorral kihagyás nélkül hozzáragaszthatjuk a baloldali sztringhez a jobboldali sztringet
indexelés: []; összefűzés: +
o logikai operátorok közül a NOT egy operandussal rendelkezik és megfordítja az operandus értékét, azaz TRUE-ből FALSE-t csinál és fordítva. Az AND művelet eredménye akkor TRUE ha mind a két operandusa TRUE, különben FALSE. Az OR operátor akkor szolgáltat TRUE értéket, ha legalább egyik operandusa TRUE. A XOR operátor akkor eredményez TRUE értéket, ha a két operandusa különböző és akkor FALSE-t, ha az operandusok értéke megegyezik
NOT AND OR XOR
o aggregált adattípusok között, amint már utaltunk rá, szintén értelmezettek
bizonyos korábban már megismert operátor jelek, ezek megléte illetve
specifikációja azonban típusonként változhat. Az indexelés, például a lista
adattípus esetében létezhet és egy számú index esetén egy lista elemet
jelképez, kettős ponttal elválasztott két index szám esetén pedig a két index
közötti elemek listáját.
A * operátort
metszetnek nevezik és a szatyor típusban alkalmazzák, eredménye pedig egy olyan
szatyor, melynek elemei mind a két operandus szatyornak tagjai.
Az összeadás különböző változatai használatosak a szatyor és lista
adattípusokban, a kivonás pedig csak a szatyor típusban. Ezek a műveletek
mindíg egy vagy több szatyor, illetve egy listaelemre vonatkoznak. A
listaelemet vagy a lista elé vagy mögé lehet beilleszteni. A kivonás a szatyor
típusra értelmezett, kivonhatunk a baloldali operandus szatyorból egy jobb
oldali operandus szatyort vagy csak egy elemet. Ha a jobboldali elem nincs
benne a baloldali szatyorban úgy az eredmény a változatlan baloldali szatyor.
A szatyor típus esetén értelmezett <= részhalmaz művelet eredménye akkor igaz, ha azok az elemek, melyek n-szer
előfordulnak a baloldali szatyorban legalább n-szer előfordulnak a
jobboldali szatyorban is.
Szintén a szatyor típusra értelmezett a >= szuperhalmaz művelet is, mely akkor igaz, ha minden elem mely n-szer
előfordul a jobboldali szatyorban legalább n-szer előfordul a
baloldaliban is (ennek a műveletnek a jelét a nagyobb egyenlővel való
összetévesztése elkerülése érdekében a jövőben É -re fogják változtatni).
A QUERY függvényt
korábban már részletesen ismertettük ezért a további magyarázataitól
eltekintünk.
Az egyenlőség jel a gyűjtő adattípusokban az értékegyenlőséget jelöli. Ez alatt
szatyor típus esetén azt értik hogy a baloldali operandus elemei ugyanannyiszor
fordulnak elő a jobboldali operandusban és fordítva. Ugyanez az operátor az
objektum példány típus esetén a megfelelő attribútum értékek azonosságát
jelöli. Az IN operátor, amint erről fentebb már szóltunk azt fejezi ki, hogy a baloldali
operandus eleme a jobboldali gyűjtő típusú objektumnak.
[ ] * + - <= >= QUERY = IN
o referenciák segítségével lehet pontosítani valamely elem azonosítását. A . karakter segítségével kapcsolhatjuk a felsorolási típus valamely eleme elé a típus deklarált nevét. Hasonlóképpen a pont karaktert használjuk arra is, hogy egy attribútumra hivatkozzunk egy objektum példányban. A pont baloldalán van az entitás példány a jobboldalán pedig a kérdéses attribútum azonosító. A \ karakter a csoport referenciákat jelöli. A back slash karakter előtt egy összetett objektum példány azonosítója helyezkedik el, míg a jobboldalán a referálni kívánt részleges összetett objektum érték objektum típusa található. Végül szólnunk kell az összetett objektum példányainak létrehozását szolgáló || konstruktor operátorról. Az operátor két oldalán a komplex objektum részek értékei helyezkednek el, melyeket az operátor kombinál.
. \ ||
Függvénydeklarációs példa.
Ismerkedésünket az EXPRESS nyelvvel fejezzük be egy olyan példával, melyben felhasználhatjuk a felvázolt elméleti ismereteket. A példát a már sokszor hivatkozott EPM Technology oktató anyagából kölcsönöztük. Mint azt már bemutattuk, az EXPRESS nyelvben -- karaktereket követően lehetőség van sor megjegyzések alkalmazására, sajnos azonban mivel az ékezetes betűk nem specifikáltak a nyelvben, kénytelenek lennénk a magyarázatokat tört magyarsággal közzétenni, ezt elkerülendő a kényelmetlenebb megoldást választjuk: először folyó szövegben elmagyarázzuk a magyarázni valókat, utána következhet a program. Az eredeti programhoz képest csak annyi a változás, hogy az elnevezett típusok nevét kis betűvel kezdjük.
A tulajdonképpeni feladatunk egy vektor típusú, local_w nevű, levezetett attribútum meghatározása érdekében elkészíteni két, három dimenziós vektor vektoriális szorzásának függvényét. A függvény típusa vektor nevű objektum, mely attribútumai egy orientation nevű 3 valós elemű lista (ez a három komponens) és egy magnitude nevű valós szám, mely a vektor hosszát jelenti.
A függvény argumentumai direction típusúak, mely attribútumai egy direction_ratios nevű 1, 2 vagy 3 valós értékből álló lista, mely valamely irányt reprezentáló vektor komponenseit, illetve az egész típusú dim, mely a vektor dimenzió számát tartalmazza.
A vektor számításból ismeretes, hogy az U(u1, u2, u3) X V(v1, v2, v3) = (u2 v3 - v2 u3) i - (u1 v3 – v1 u3) j + (u1 v2 – v1 u2) k.
A helyi munka változók deklarálása után az EXISTS(v) függvénnyel megnézzük, hogy határoztt-e az arg1 és arg2 formális paraméterek aktuális értéke, illetve hogy a dimenzió számaik nem egyenlők-e kettővel. Ha ugyanis legalább az egyik argumentum határozatlan vagy kétdimenziós, úgy a függvény határozatlan értéket (?) ad vissza (már itt megfigyelhetjük a RETURN használatát).
Ezután egy már korábban meghatározott normalizáló függvény felhasználásával az első és második paraméter hosszát az egységre redukáljuk és a komponenseket elhelyezzük a v1, v2 munkaváltozókban. Érdekes megfigyelni, hogy a pont '.' segítségével miként tesszük határozottá a pontot követő attribútumot azzal hogy a tulajdonos objektum példányt (mely esetünkben egy függvény érték) elé írjuk.
A következő lépésben meghatározzuk a res lokális objektum direction_ratios lista típusú attribútumának elemeit a vektoriális szorzásra fentebb közölt képlet felhasználásával.
Ezután inkrementális vezérlésű ciklus utasítással meghatározzuk az eredmény vektor komponenseinek négyzetösszegét (az önmagával történő szorzás helyett alkalmazhattuk volna a '**2' operátort is). Ha az eredmény nagyobb mint 0, akkor a komponensek illetve a nagyság értéket, melyet a négyzetösszegből gyökvonással kaptunk hozzárendeljük a result lokális objektum megfelelő attribútumaihoz.
Ha az eredő vektor hossza 0 akkor a két operandus vektor párhuzamos egymással és az eredmény komponensek megegyeznek valamelyik, esetünkben az arg1 aktuális komponenseivel, a vektor nagysága pedig értelemszerűen zérus. Végül ezekre az esetekre is visszaadjuk a függvényértéket (RETURN(result)), lezárjuk az összetett utasítást, lezárjuk az első IF elágazást és lezárjuk magát a függvény deklarációt.
local_u : direction;
local_v : direction;
DERIVE
local_w: vector := cross_product(local_u, local_v);
FUNCTION cross_product (arg1, arg2 : direction) : vector;
LOCAL
mag : REAL;
res : direction;
v1,v2 : LIST[3:3] OF REAL;
result : vector;
END_LOCAL;
IF ( NOT EXISTS (arg1) OR (arg1.dim = 2)) OR
( NOT EXISTS (arg2) OR (arg2.dim = 2)) THEN
RETURN(?);
ELSE
BEGIN
v1 := normalise(arg1).direction_ratios;
v2 := normalise(arg2).direction_ratios;
res.direction_ratios[1] := (v1[2]*v2[3] - v1[3]*v2[2]);
res.direction_ratios[2] := (v1[3]*v2[1] - v1[1]*v2[3]);
res.direction_ratios[3] := (v1[1]*v2[2] - v1[2]*v2[1]);
mag := 0.0;
REPEAT i := 1 TO 3;
mag := mag + res.direction_ratios[i]*res.direction_ratios[i];
END_REPEAT;
IF (mag > 0.0) THEN
result.orientation := res;
result.magnitude := SQRT(mag);
ELSE
result.orientation := arg1;
result.magnitude := 0.0;
END_IF;
RETURN(result);
END;
END_IF;
END_FUNCTION;
A függvény deklarációban felhasználtuk a korábban már deklarált
FUNCTION normalise (arg : vector_or_direction) : vector_or_direction; normalizáló függvényt.
Megismételjük: rövid összefoglalásunk célja kizárólag az volt, hogy felkeltsük az érdeklődést, átfogó képet adjunk és megkönnyítsük az EXPRESS specifikációk olvasását. Aki maga is EXPRESS specifikációk írására készül, annak feltétlenül szüksége van a nyelv hivatalos leírásának (STEP szabvány 1.1 fejezet) további elmélyült tanulmányozására.
Azok számára, akik a nyelvet valóban információ modellezésre használják jelentős könnyebbséget jelent a NIST Expresso nevű ingyenes szoftver, mely komoly segítséget nyújt a modellek létrehozásához és hitelesítéséhez.
· a következő részben megismerkedünk a magyar térinformatikai csereformátum szabvánnyal
· esetleg visszatérhet az előző részhez
· illetve a tartalomjegyzékhez
Megjegyzéseit E-mail-en várja a szerző: Dr Sárközy Ferenc